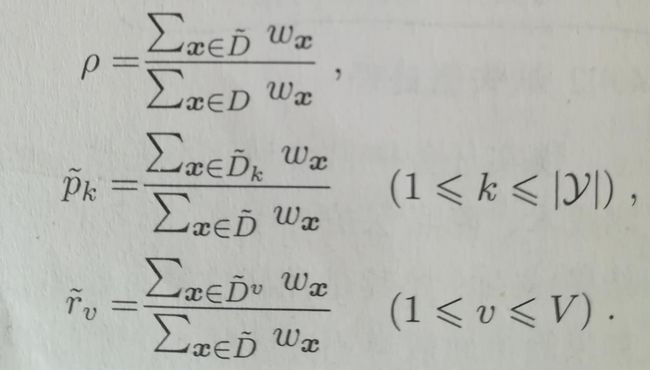机器学习:决策树-基础算法,剪枝,连续值缺失值处理,多变量决策树(附代码实现)
基础算法
举个栗子:
当一个有经验的老农看一个瓜是不是好瓜时,他可能会先看下瓜的颜色,一看是青绿的,心想有可能是好瓜!接着他又看了下根蒂,发现是蜷缩着的,老农微微点头,寻思着五成以上是好挂瓜!最后他又敲了下瓜,一听发出浑浊的响声,高兴的叫到:这瓜是个好瓜啊!这就是老农做出决策的大致过程。
代码的形式表示:
划分属性选择
上图算法最重要的一行就是第8行:从A中选择最优的划分属性a*。
一般希望决策树层数越少,分支越少,尽快的做出决策,这就要求结点包含的样本尽可能属于同一类,即结点“纯度”尽量高。
这也符合老农挑瓜的经验:
当老农看了下瓜的根蒂,发现根蒂是蜷缩的,老农回想了下过往他看过的成千上万的瓜,记得根蒂只要是蜷缩的瓜都是好瓜(结点“纯度”很高,所有样本属于同一个分类),他不需要再听瓜的声音,就可以直接做出判断:哈哈,这是个好瓜啊!相反,如果老农回想了过往的那些瓜,发现根蒂是蜷缩的瓜既有好瓜也有坏瓜(结点“纯度”较低,样本属于两个分类),那他肯能就需要再敲下瓜,听听瓜的声音再做出的判断。
最优划分的选择一般有“信息增益”和“基尼指数”等指标。
信息增益(C4.5决策树)
信息熵:度量样本集合的纯度。假定样本集合D中第k类样本所占比例为pk(k=1,2,...,|y|),则D的信息熵为:
信息熵越小,则D的纯度越高。
信息增益:假定离散属性a有V个属性值{a1,a2,...,aV},若用a对样本划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为aV的样本,记为Dv。则可以计算出Dv的信息熵,并赋予权重|Dv|/|D|,则可计算出用属性a对样本D进行划分的信息增益:
信息增益越大,纯度提升越大。所以这样来选择最优属性:a* = arg max Gain(D,a)(使信息增益最大的属性a)。
增益率:
著名的C4.5决策树算法没有直接使用信息增益,而是使用的增益率。因为信息增益准则对可取数目较多的属性有所偏好,而这种偏好可能带来不利影响。可以想像,在极端情况下,如果一个数据集D有100个样本,在某属性上有100个不同取值,则该属性上全部信息熵之和为0,即信息增益为最大值Ent(D),显然决策树会对该属性有所偏好。
需要注意的是,增益率对属性数目较少的属性有所偏好,所以C4.5算法也没有直接使用增益率,而是先从属性中找到信息增益高于平均水平的属性,再从中选择增益率最高的。
基尼指数(CART决策树)
基尼值:
基尼值越小,数据集D的纯度越高。
基尼指数:
选择基尼指数最小的属性作为最优划分属性,即a* = arg min Gini_index(D,a).
剪枝处理——避免过拟合
剪枝是为了解决决策树“过拟合”的手段,当一颗决策树分支、层数过多,就容易出现”过拟合“,导致决策树泛化性能不好。剪枝分为“预剪枝”和“后剪枝”。
预剪枝:在决策树生成过程中,在每个结点划分前先估计,若当前结点的划分不能带来泛化性能的提升,就停止划分,把当前结点标记为叶结点。
后剪枝:先生成完整的决策树,之后再自底向上对非叶结点考察,若该结点对应的子树替换为叶结点能提升泛化性能,则将其替换为叶结点。
预剪枝处理方式如下图。假如基于信息增益的准则,我们首先选择了“脐部”作为划分准则。在划分前,所有样本都在根结点1。若不进行划分,则将该结点标记为叶结点,类别为训练集中样本最多的类别,假设是“好瓜”。再用验证集去评估这个单结点决策树,假设正确率为42.9%。接着,我们对“脐部”进行划分,得到结点2,3,4,假设分别对应“好瓜”,“好瓜”,“坏瓜”。再用验证集去评估新的决策树,假设得到正确率71.4%>42.9%,则用“脐部”进行划分得以确定。重复以上步骤生成最终的决策树。
预剪枝优缺点:降低“过拟合”风险,减少时间开销。但是,有些分支当前划分虽不能提升泛化性能,但在其基础上进行的后续划分可能导致性能显著提升,所以可能会带来“欠拟合”的风险。(有点像梯度下降,追求每一步的最快下降,只顾眼前,但可能只能达到局部最优)。
后剪枝过程如下面两图所示。首先生成第一幅图完整的决策树,假设根据验证集得到其正确率为42.9%。接着考察最底下的结点6,若将器分支剪除,相当于把6替换为叶结点,假设其类别为“好瓜”,再用验证集评估新的决策树,假设准确率为57.1%,则后剪枝策略决定剪枝。再考察结点5,以此类推,得到最终的决策树。
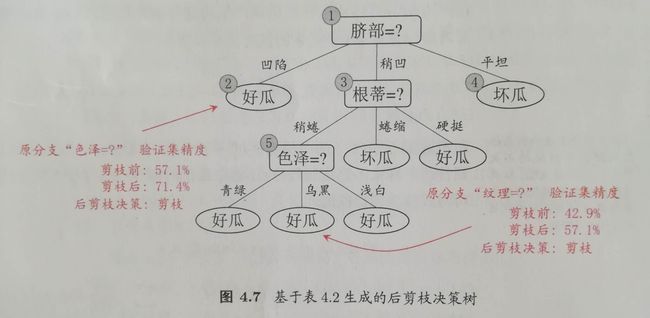
后剪枝优缺点:一般情况下,“欠拟合”风险很小,泛化性能往往优于预剪枝。但是时间开销比预剪枝大得多。
连续值处理
对于连续属性(如密度,面积,价格等),其属性值数目无限,不能直接根据连续属性的可取值进行划分。
最简单的策略是“二分法”(C4.5采用):假定样本集D和连续属性a,a在D上有n个不同取值,将这些取值从下到大排列,记为{a1,a2,...,an},选择划分点t可将D划分为D-和D+,D-包含取值不大于t的样本,D+包含取值大于t的样本,可以得到n-1个候选划分点:Ta={[a(i)+a(i+1)]/2|1<=i<=n-1},将信息增益改造成如下公式:
选择使Gain(D,a,t)最大化的划分点t。可以得到如下图所示的决策树:
注:与离散属性不同,若当前节点划分属性为连续值,该属性还可作为后代结点的划分属性(如此处使用了密度<=0.381,不会禁止在子结点使用如密度<=0.294)。
缺失值处理
经常会碰到数据集中某些数据的属性值未知,这时候就要解决两个问题:1、怎么选择划分属性?2、划分属性确定后,怎么把该属性未知的数据划分到结点?
假定D'表示D中在属性a上没有缺失值的样本子集。对于第一个问题,我们只能根据D'来判断属性的优劣。假定属性a有V个可取值,D'v表示D'中在属性a上取值为aVd 样本子集,D'k表示D'中第k(k=1,2,...,|y|)类的样本子集,我们为每个样本赋予一个权重wx。定义以下变量:
对于第二个问题,若样本在划分属性a上取值已知,就把样本划分到对应的子结点,并且权重保持wx不变。若样本在属性a上取值未知,则把它划分到所有的子结点,并且权重在子结点调整为r'v*wx(r'v指的是图中r波浪v下标),同一个样本以不同的概率划入不同的结点。
多变量决策树(斜决策树)
决策树形成的分类边界有一个明星的特点:轴平行。如下面这颗决策树: 它形成的分类边界如下图所示:
它形成的分类边界如下图所示:
 当分类边界比较复杂时,要有很多段的划分才能得到近似,所形成的决策树就会很复杂。
当分类边界比较复杂时,要有很多段的划分才能得到近似,所形成的决策树就会很复杂。
多变量决策树是为了实现“斜划分”,减少划分段数。它不以单个属性进行划分,而是每个分类结点是一个形如(w1*a1+w2*a2+...+wd*ad)= t的一个线性分类器,wd是属性ad的权重,w和t在该结点所含样本集和属性集学得。所以多变量分类器就变成为每个结点寻找合适的线性分类器。
生成决策树matlab代码(包括连续值的“二分法”处理):
注:代码里的attrs是这样一个事先处理好的一个结构:
color = struct('attr_k',1,'attr_type',0,'values',{[1,0,0],[0,1,0],[0,0,1]});
rootbase = struct('attr_k',2,'attr_type',0,'values',{[1,0,0],[0,1,0],[0,0,1]});
voice = struct('attr_k',3,'attr_type',0,'values',{[1,0,0],[0,1,0],[0,0,1]});
texture = struct('attr_k',4,'attr_type',0,'values',{[1,0,0],[0,1,0],[0,0,1]});
umbilicus = struct('attr_k',5,'attr_type',0,'values',{[1,0,0],[0,1,0],[0,0,1]});
touch = struct('attr_k',6,'attr_type',0,'values',{[1,0],[0,1]});
density = struct('attr_k',7,'attr_type',2,'values','');
sugar = struct('attr_k',8,'attr_type',2,'values','');
attrs = {color,rootbase,voice,texture,umbilicus,touch,density,sugar};轻微吐槽:matlab的struct结构好怪异,对matlab不熟,写的挺纠结,不知道大神们有什么建议。
代码开始:
function [tree] = maketreeFunc(x,y,attrs)
%生成结点
tree = struct('parent_attr_val',struct('symbol','','value',''),'div_attr',struct('attr_k','','attr_type',0),'cate','no','child',cell(1));
node = tree;
%属于同一分类,生成叶结点
if isequal(y,ones(length(y),1)*y(1)),
%叶结点
tree.cate = y(1);
return;
endif;
%判断所有属性是否都相同
is_attr_same = 1;
if length(attrs)>0,
for i=1:length(attrs),
for j=2:length(y),
if ~isequal(x{1,attrs{i}(1).attr_k},x{j,attrs{i}(1).attr_k}),
is_attr_same = 0;
break;
endif;
endfor;
if is_attr_same==0,
break;
endif;
endfor;
endif;
%属性集为空或所有属性值都相同,生成叶结点
if length(attrs)==0||is_attr_same,
%找到类别比重最多的一类作为叶结点
t = tabulate(y+1);
max_percent = max(t(:,3));
[row,col] = find(t == max_percent,1);
most_y = t(row,1)-1;
%叶结点
tree.cate = most_y;
return;
endif;
%信息熵
info_entropy = infoentropyFunc(y);
%不同属性的信息增益矩阵
info_gain = [];
%确定划分属性
for i=1:length(attrs),
attr_col = x(:,attrs{i}(1).attr_k);
y_cate = {};
L = 1;
%连续属性二分法处理
if attrs{i}(1).attr_type == 2,
attr_col_mat = cell2mat(attr_col);
%升序
attr_col_mat = sort(attr_col_mat,'ascend');
%划分点集合
bi_part = [];
for j=1:(length(attr_col_mat)-1),
bi_part(j) = (attr_col_mat(j)+attr_col_mat(j+1))/2;
endfor;
%不同划分点信息增益矩阵
bi_gain = [];
for j=1:length(bi_part),
left_cate_y = [];
right_cate_y = [];
for k=1:length(attr_col),
if attr_col{k}<=bi_part(j),
left_cate_y = [left_cate_y;y(k)];
else
right_cate_y = [right_cate_y;y(k)];
endif;
endfor;
attr_entropy = 0;
attr_entropy += (length(left_cate_y)/length(y))*infoentropyFunc(left_cate_y);
attr_entropy += (length(right_cate_y)/length(y))*infoentropyFunc(right_cate_y);
bi_gain(j) = info_entropy - attr_entropy;
endfor;
%划分点中信息增益最大的划分点作为该属性的最终信息增益
max_bi_pos = find(bi_gain==max(bi_gain),1);
info_gain(1,i) = max(bi_gain);
info_gain(2,i) = bi_part(max_bi_pos);
else%非连续属性
for j=1:length(attrs{i}),
one_cate_y = [];
for k=1:length(attr_col),
if attrs{i}(j).values==attr_col{k},
one_cate_y = [one_cate_y;y(k)];
endif;
endfor;
if length(one_cate_y)>0,
y_cate(L) = one_cate_y;
L = L+1;
endif;
endfor;
attr_entropy = 0;
for m=1:length(y_cate),
attr_entropy += (length(y_cate{m})/length(y))*infoentropyFunc(y_cate{m});
endfor;
info_gain(1,i) = info_entropy - attr_entropy;
endif;
%info_gain(i) = struct('gain',info_entropy - attr_entropy,'attr',attrs(i));
endfor;
%取最大的信息增益属性
pos = find(info_gain(1,:)==max(info_gain(1,:)),1);
%记录划分属性
tree.div_attr.attr_k = attrs{pos}(1).attr_k;
tree.div_attr.attr_type = attrs{pos}(1).attr_type;
%生成分支
if attrs{pos}(1).attr_type==2,%连续属性
%二分法生成的划分点
part_num = info_gain(2,pos);
%生成大于和小于划分点的两个分支
for i=1:2,
x_part = {};
y_part = [];
k = 1;
for j=1:length(x(:,attrs{pos}(1).attr_k)),
%小于part_num的部分
if i==1,
if x(:,attrs{pos}(1).attr_k){j}<=part_num,
x_part(k,:) = x(j,:);
y_part(k,1) = y(j);
k = k + 1;
endif;
else%大于part_num的部分
if x(:,attrs{pos}(1).attr_k){j}>part_num,
x_part(k,:) = x(j,:);
y_part(k,1) = y(j);
k = k + 1;
endif;
endif;
endfor;
%连续属性子结点可以继续划分,无需清除该属性
%child_attrs = attrs;
%child_attrs(pos) = [];
[child_tree] = maketreeFunc(x_part,y_part,attrs);
if i==1,
child_tree.parent_attr_val.symbol = '<';
else
child_tree.parent_attr_val.symbol = '>';
endif;
child_tree.parent_attr_val.value = part_num;
len = length(tree.child);
tree.child(len+1) = child_tree;
endfor;
else%非连续属性
%不同属性值生成分支
for i=1:length(attrs{pos}),
flag = 0;
x_part = {};
y_part = [];
k = 1;
%一个分支的x,y数据集
for j=1:length(x(:,attrs{pos}(1).attr_k)),
if isequal(attrs{pos}(i).values,x(:,attrs{pos}(1).attr_k){j}),
flag = 1;
x_part(k,:) = x(j,:);
y_part(k,1) = y(j);
k = k + 1;
endif;
endfor;
%分支数据为空,生成叶结点
if flag==0,
%找到类别比例最多的类别
t = tabulate(y+1);
max_percent = max(t(:,3));
[row,col] = find(t == max_percent,1);
most_y = t(row,1)-1;
%生成叶结点
node.cate = most_y;
node.parent_attr_val.value = attrs{pos}(i).values;
len = length(tree.child);
tree.child(len+1) = node;
return;
endif;
child_attrs = attrs;
%子结点中删除当前用于划分的属性
child_attrs(pos) = [];
%生成子结点
[child_tree] = maketreeFunc(x_part,y_part,child_attrs);
child_tree.parent_attr_val.value = attrs{pos}(i).values;
len = length(tree.child);
tree.child(len+1) = child_tree;
endfor;
endif; 微信交流
微信交流  多谢打赏
多谢打赏
参考资料:周志华《机器学习》