机器学习算法——k-均值聚类算法对未标注数据分组
k-均值聚类算法对未标注数据分组
-
- 0、前言
- 1、k-均值聚类算法
- 2、对于k-means的算法优化
-
- 2.1对聚类得到的簇进行二次处理
- 2.2二分k-均值聚类算法
- 3、对纽波兰的地理位置进行聚类
-
- 3.1我们按照以下几个流程完成项目:
- 3.2具体代码实现
- 4、小结
- 学习永无止境,后续还会有更多的算法学习及实例尝试。
0、前言
聚类是一种无监督的学习,它将相似的对象归到同一簇中。它有点像全自动分了。聚类方法几乎可以应用到所有对象,簇内的对象越相似,聚类的效果越好。本章要学习一种称为K-均值(K-means)聚类的算法。之所以称之为K-均值是因为它可以发现k个不同的簇,且每个簇的中心采用簇中所含值的均值进行计算而成。
聚类与分类的最大不同在于,分类的目标事先已知,而聚类则不一样。因为其产生的结果与分类相同,而只是类别没有预先定义,聚类有时也被称为无监督分类(umsupervised classification)
聚类分析试图将相似对象归入同一簇,将部相似的对象归到不同的簇。相似这一概念取决于所选择的相似度计算方法。到底使用哪种相似度计算方法取决于具体的应用。
我们先来看一下什么是簇识别,簇识别给出聚类结果的含义,假定有一些数据,现在将相似数据归到一起,簇识别会告诉我们这些簇到底都是些什么。聚类与分类的最大不同在于,分了的目标事先已知,而聚类则不一样,因为其产生的结果与分类相同,而只是类别没有预先定义,因此,聚类有时也称为无监督分类。聚类分析尝试将相似对象归入同一簇,将不相似对象归到不同簇。各个样本间是否相似,取决于相似度的计算方法。
k-均值聚类算法
优点:容易实现
缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢
适用数据类型:数值型数据
k-均值是发现给定数据集的k个簇的算法,簇个数k是用户给定的,每个簇通过其质心,因此,每个簇的所有点由其质心(中心)描述。
本文所用到的所有数据集材料:
链接:百度网盘
提取码:01gm
1、k-均值聚类算法
K-均值是发现给定数据集的k个簇的算法,k由用户给定。
K-means算法工作流程:
- 随机选定k个初始点作为质心(即簇中所有点的中心)
- 为数据集中每个点找到距其最近的质心,并将其分配到该质心所对应的簇
- 每个簇的质心更新为该簇所有点的平均值
值得注意的是,实现无监督学习过程中,没有显著式的训练流程,其训练过程与推理过程融为一体。
伪代码如下:
随机选择k个点作为初始质心
当任意一个点的簇分配结果发生改变时:
对数据集中的每个数据点:
对每个质心:
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将其作为质心
import numpy as np
import urllib
import json
import time
import matplotlib.pyplot as plt
def loadDataSet(fileName): # 按 Tab键 分割成 列表
"""
函数说明:载入数据
Parameter:
filename:文件名
Return:
dataMat:数据集
"""
dataMat = [] # 假设最后一列是目标值
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float, curLine)) # 每行数据映射为一个浮点型的值
dataMat.append(fltLine)
return dataMat
def distEclud(vecA, vecB):
# 计算两个向量的欧式距离
return np.sqrt(np.sum(np.power(vecA - vecB, 2)))
def randCent(dataSet, k):
"""
改函数为给定数据集构建一个包含k个随机质心的集合,随机质心必须要在整个数据集的边界内
通过找到数据集每一维度的最值,以确保随机点在数据的边界之内
:param dataSet:
:param k:
"""
n = np.shape(dataSet)[1]
centroids = np.mat(np.zeros((k, n))) # 为质心预分配空间
for j in range(n): # 创建簇质心
minJ = min(dataSet[:, j])
rangeJ = float(max(dataSet[:, j]) - minJ)
centroids[:, j] = np.mat(minJ + rangeJ * np.random.rand(k, 1))
return centroids
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
"""
k-均值算法
:param dataSet: 数据集
:param k: 聚类数量
:param distMeas:计算距离的函数,此处使用的欧式空间距离
:param createCent: 初始质心的函数
:return: centroids 质心, clusterAssment 簇分配结果矩阵
clusterAssment包含两列,一列记录簇索引值,第二列存储误差,这里的误差指的是当前点到簇质心的距离
可以据此误差评价聚类的效果
"""
m = np.shape(dataSet)[0]
clusterAssment = np.mat(np.zeros((m, 2)))
centroids = createCent(dataSet, k)
clusterChanged = True
optimization = 1
while clusterChanged:
clusterChanged = False
for i in range(m):
minDist = np.inf
minIndex = -1
for j in range(k): # 寻找最近的质心
distJI = distMeas(centroids[j, :], dataSet[i, :])
if distJI < minDist:
minDist = distJI
minIndex = j
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist ** 2
print("\n optimization : ", optimization)
optimization += 1
print(centroids)
for cent in range(k): # 更新质心位置
ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]] # 获取该簇中所有的点
centroids[cent, :] = np.mean(ptsInClust, axis=0) # 将质心更新为均值
return centroids, clusterAssment
def showPlt(datMat, alg=kMeans, numClust=4):
"""
绘制出聚类的结果
:param datMat: 输入待聚类的数据
:param alg: 使用的聚类方法
:param numClust: 聚类簇数量
"""
myCentroids, clustAssing = alg(datMat, numClust)
fig = plt.figure()
rect = [0.1, 0.1, 0.8, 0.8]
scatterMarkers = ['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<'] # 描点所用到的标记符
axprops = dict(xticks=[], yticks=[])
ax0 = fig.add_axes(rect, label='ax0', **axprops)
ax1 = fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[np.nonzero(clustAssing[:, 0].A == i)[0], :]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:, 0].flatten().A[0], ptsInCurrCluster[:, 1].flatten().A[0], marker=markerStyle,
s=90)
ax1.scatter(myCentroids[:, 0].flatten().A[0], myCentroids[:, 1].flatten().A[0], marker='+', s=300)
plt.show()
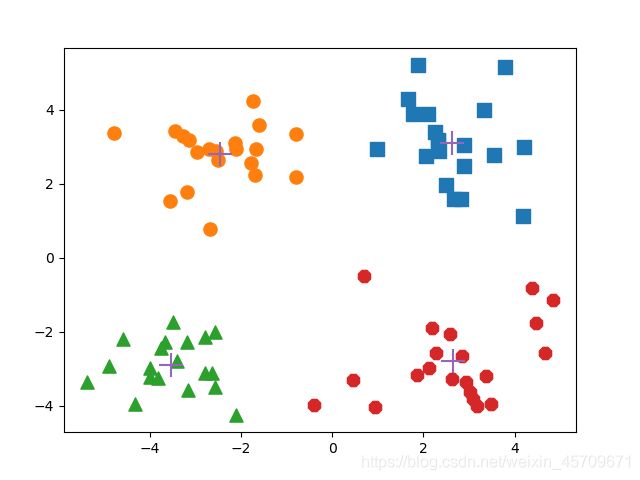
datMat = np.mat(loadDataSet('testSet.txt'))
# myCentroids, clustAssing = kMeans(datMat, 4)
showPlt(datMat=datMat)
optimization : 1
[[ 2.20613332 2.1193681 ]
[-1.88460231 -0.05466263]
[-2.62481439 -2.17381403]
[-0.37574698 -3.05111428]]
optimization : 2
[[ 2.72627338 2.57409117]
[-2.38682555 2.5962443 ]
[-3.61853111 -2.81946867]
[ 2.17502517 -3.25603011]]
optimization : 3
[[ 2.6265299 3.10868015]
[-2.46154315 2.78737555]
[-3.53973889 -2.89384326]
[ 2.65077367 -2.79019029]]
2、对于k-means的算法优化
2.1对聚类得到的簇进行二次处理
我们知道,k-means的k是一个超参数,由用户预定义,但是我们有时候并不知道k的选择是否正确,在包含簇分配结果的矩阵中保存着每个点的误差,也就是该点到簇质心的距离平方值。
有时候,k-means收敛到了局部最小值,而非全局最小值,这也使得算法的聚类效果不佳。我们可以利用SSE(Sum of Squared Error , 误差平方和)来度量聚类效果。显而易见的是,增加簇的个数可以降低SSE,然而这与我们的目标或者说聚类的目标不符。聚类的目标是在保持簇数目不变的情况下增加分类簇的效果。
为了解决该问题,我们可以对生成的簇进行后处理,一种方法是将具有最大SSE值的簇划分为两个,也就是把那些导致最大SSE的数据点分离出来,再次执行k-means二聚类。
另一方面,为了保持簇总数不变,我们可以将某两个簇合并,例如我们可以合并最近的质心,或者也可以合并两个使得SSE增幅最小的质心。前一种思路通过计算所有质心之间的距离,然后合并距离最近的两个点来实现,后一种则需要合并两个簇然后计算总SSE值。值得注意的是,我们必须在所有可能的两个簇上重复上述的处理过程,这需要较大的计算量,直到找到合并最佳的两个簇为止。
2.2二分k-均值聚类算法
为克服k-均值算法收敛于局部最小值的问题,我们选择二分K-均值算法。该算法首先将所有点视作一个簇,然后一分为二,之后选择其中一个簇继续进行划分,选择哪个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。
算法的伪代码如下:
将所有点看成一个簇
当簇数目小于预设的k时:
对于每个簇
计算总误差
在给定的簇上进行k-均值算法(k=2)
计算将该簇一分为二后的总误差
选择使得误差最小的那个簇进行划分操作
还有一种做法,选择SSE最大的簇进行划分,直到簇数目达到用户指定的数目为止。
其实现代码如下:
def biKmeans(dataSet, k, distMeas=distEclud):
"""
函数说明:二分K均值算法
Parameters:
dataSet:数据集
k:待分类别数
distMeas:距离计算
Returns:
centList:质心列表
clusterAssment:样本分配结果
"""
m = np.shape(dataSet)[0] # 样本个数
clusterAssment = np.mat(np.zeros((m, 2))) # 初始化样本分配结果
centroid0 = np.mean(dataSet, axis=0).tolist()[0] # 创建第一个初始质心
centList = [centroid0] # 初始化质心列表
for j in range(m): # 计算初始误差
clusterAssment[j, 1] = distMeas(np.mat(centroid0), dataSet[j, :]) ** 2
while (len(centList) < k): # 未达到指定质心数,就继续迭代
lowestSSE = np.inf # 初始化最小SSE
for i in range(len(centList)): # 对于质心列表中的每个质心
ptsInCurrCluster = dataSet[np.nonzero(clusterAssment[:, 0].A == i)[0], :]
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # 对此质心内的样本点进行二分类
# 该样本中心 二分类之后的 误差平方和 SSE
sseSplit = sum(splitClustAss[:, 1])
# 其他未划分数据集的误差平方和 SSE
sseNotSplit = sum(clusterAssment[np.nonzero(clusterAssment[:, 0].A != i)[0], 1])
print("sseSplit, and notSplit:", sseSplit, sseNotSplit)
# 划分后的误差和没有进行划分的数据集的误差之和为本次误差
if (sseSplit + sseNotSplit) < lowestSSE:
bestCentToSplit = i # 记录应该被划分的中心的索引
bestNewCents = centroidMat # 最好的新划分出来的中心
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit # 更新总的误差平方和
bestClustAss[np.nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)
bestClustAss[np.nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit
print("the bestCentToSplit is:", bestCentToSplit)
print("the len of bestClustAss is:", len(bestClustAss))
# 将最应该被划分的中心 替换为 划分后的 两个 中心(一个替换,另一个 append在最后添加)
centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0] # 替换
centList.append(bestNewCents[1, :].tolist()[0])
# 更新样本分配结果
clusterAssment[np.nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0], :] = bestClustAss
return np.mat(centList), clusterAssment
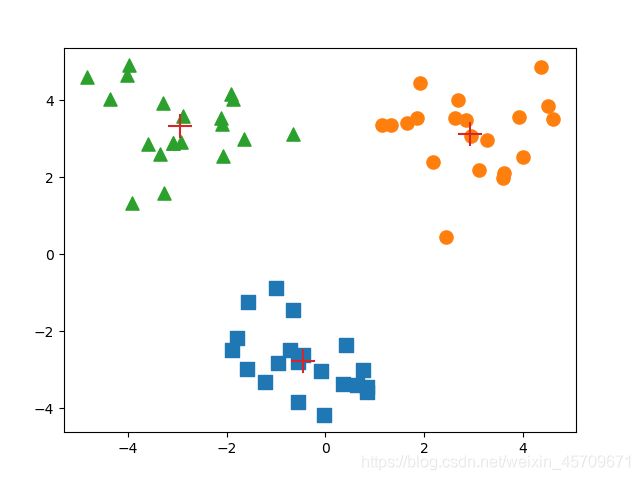
datMat2 = np.mat(loadDataSet('testSet2.txt'))
# centlist, myNewAssments = biKmeans(datMat2, 3)
showPlt(datMat2, alg=biKmeans, numClust=3)
输出优化过程的日志:
optimization : 1
[[ 1.78556179 -2.91907791]
[ 2.43075886 4.08358847]]
optimization : 2
[[-0.32150057 -2.62473743]
[-0.06953469 3.29844341]]
optimization : 3
[[-0.45965615 -2.7782156 ]
[-0.00675605 3.22710297]]
sseSplit, and notSplit: [[453.03348958]] 0
the bestCentToSplit is: 0
the len of bestClustAss is: 60
optimization : 1
[[-0.82568588 -3.14289681]
[-1.30746525 -2.59325768]]
optimization : 2
[[-7.11923077e-04 -3.21792031e+00]
[-1.31198114e+00 -1.96162114e+00]]
optimization : 3
[[ 0.07973025 -3.24942808]
[-1.26873575 -2.07139688]]
optimization : 4
[[ 0.19848727 -3.24320436]
[-1.26405367 -2.209896 ]]
optimization : 5
[[ 0.2642961 -3.3057243]
[-1.1836084 -2.2507069]]
optimization : 6
[[ 0.35496167 -3.36033556]
[-1.12616164 -2.30193564]]
sseSplit, and notSplit: [[12.75326314]] [[423.87624014]]
optimization : 1
[[ 1.30457434 2.52771537]
[-1.22941241 3.67981002]]
optimization : 2
[[ 2.93386365 3.12782785]
[-2.94737575 3.3263781 ]]
sseSplit, and notSplit: [[77.59224932]] [[29.15724944]]
the bestCentToSplit is: 1
the len of bestClustAss is: 40
改函数可以运行多次,聚类会收敛到全局最小值,而原始的kMeans()偶尔会陷入局部最小值。
3、对纽波兰的地理位置进行聚类
现在,我们需要在一晚上前往70个地方,这些位置主要分布在纽波兰城市的附近,我们计划将之聚类为几类,然后先利用交通工具前往这些簇的质心,然后步行到不同的位置去,我们需要这70个地方的经纬度,接下来,我们将利用前面的算法完成旅途安排。
3.1我们按照以下几个流程完成项目:
(1)收集数据,使用Yahoo!PlaceFinder API转换经纬度信息
(2)准备数据,只保留经纬度信息
(3)分析数据,使用Matplotlib来构建一个二维数据图,其中包含簇与地图
(4)测试算法,利用bikmeans(),值得注意的是这一步隐式的包含了训练
(5)使用算法:最后输出包含簇及簇中心的地图
3.2具体代码实现
具体的代码实现时有以下两个困难点:
(1)我们使用雅虎提供的Yahoo!PlaceFinder API完成我们的需求。为了使用该服务,需要注册以获得一个API key,前往Yahoo!开发者网络中注册,创建一个桌面应用后会获得一个appid。我们再利用appid使用geocoder。一个geocoder接受给定地址,然后返回该地址对应的经纬度。
def geoGrab(stAddress, city):
apiStem = 'http://where.yahooapis.com/geocode?' # 为goecoder创建字典和常量
params = {}
params['flags'] = 'J' # JSON 返回类型
params['appid'] = 'aaa0VN6k'
params['location'] = '%s %s' % (stAddress, city)
url_params = urllib.parse.urlencode(params)
yahooApi = apiStem + url_params # 打印url参数
print(yahooApi)
c = urllib.request.urlopen(yahooApi)
return json.loads(c.read())
def massPlaceFind(fileName):
"""
改函数打开一个tab分隔的文本文件,在本例中,该文件存储着需要去的70个地方的地理信息
获取第2,3列结果后,被输入到函数geoGrab()中,然后检查geoGrab()的输出字典判断有无错误
如若无误,就可以从字典中读取经纬度信息,并添加到原来对应的行上,同时写到新文件中
:param fileName:
:return:
"""
fw = open('places.txt', 'w')
for line in open(fileName).readlines():
line = line.strip()
lineArr = line.split('\t')
retDict = geoGrab(lineArr[1], lineArr[2])
if retDict['ResultSet']['Error'] == 0:
lat = float(retDict['ResultSet']['Results'][0]['latitude'])
lng = float(retDict['ResultSet']['Results'][0]['longitude'])
print("%s\t%f\t%f" % (lineArr[0], lat, lng))
fw.write('%s\t%f\t%f\n' % (line, lat, lng))
else:
print("error fetching")
time.sleep(1) # 为防止过于频繁调用API被封
fw.close()
(2)现在我们有一个包含格式化地理坐标的列表,接下来可以对这些俱乐部进行聚类,在此过程中使用雅虎API来获得每个点的经纬度信息。这个例子中要聚类的俱乐部给出的信息为经纬度,但这些信息对于计算距离还不够,经纬度的变化会使得距离变化发生较大差异,北极附近每走几米的经度变化可能达到数10度,而在赤道附近走相同的距离,带来的经度变化可能只是零点几,因此我们需要用球面余弦定理来计算两个纬度之间的距离。
def distSLC(vecA, vecB):
"""
返回地球表面两个点的经纬度,可以使用球面余弦定理来计算两点的距离
此处的经纬度使用角度制,但sin,cos需要转换后使用
:param vecA: :param vecB: 两个点的经纬度
:return: 两点的距离
"""
a = np.sin(vecA[0, 1] * np.pi / 180) * np.sin(vecB[0, 1] * np.pi / 180)
b = np.cos(vecA[0, 1] * np.pi / 180) * np.cos(vecB[0, 1] * np.pi / 180) * \
np.cos(np.pi * (vecB[0, 0] - vecA[0, 0]) / 180)
return np.arccos(a + b) * 6371.0 # pi由numpy提供
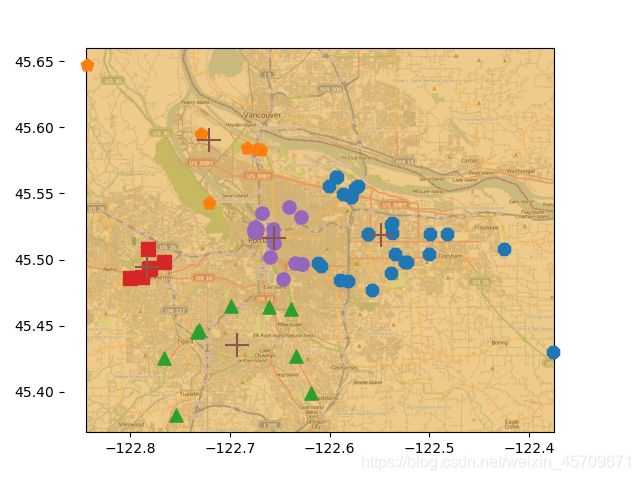
def clusterClubs(numClust=5):
"""
默认聚类为5个簇,然后在地图上绘制出70个点,利用matplotlib绘制散点图区分不同的簇
:param numClust: 默认聚类为5个簇
"""
datList = []
for line in open('places.txt').readlines():
lineArr = line.split('\t')
datList.append([float(lineArr[4]), float(lineArr[3])])
datMat = np.mat(datList)
myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC)
fig = plt.figure()
rect = [0.1, 0.1, 0.8, 0.8]
scatterMarkers = ['8', 'p', '^', 's', 'o', 'd', 'v', 'h', '>', '<']
axprops = dict(xticks=[], yticks=[])
ax0 = fig.add_axes(rect, label='ax0', **axprops)
imgP = plt.imread('Portland.png')
ax0.imshow(imgP)
ax1 = fig.add_axes(rect, label='ax1', frameon=False)
for i in range(numClust):
ptsInCurrCluster = datMat[np.nonzero(clustAssing[:, 0].A == i)[0], :]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:, 0].flatten().A[0], ptsInCurrCluster[:, 1].flatten().A[0], marker=markerStyle,
s=90)
ax1.scatter(myCentroids[:, 0].flatten().A[0], myCentroids[:, 1].flatten().A[0], marker='+', s=300)
plt.show()
clusterClubs(5)
optimization : 1
[[-122.4511744 45.49798317]
[-122.61249549 45.40894812]]
optimization : 2
[[-122.55039411 45.52749554]
[-122.68718593 45.50193383]]
optimization : 3
[[-122.54868607 45.51882187]
[-122.69551477 45.50729503]]
sseSplit, and notSplit: [[3043.26331611]] 0
the bestCentToSplit is: 0
the len of bestClustAss is: 69
optimization : 1
[[-122.5955164 45.55613783]
[-122.38256424 45.48613604]]
optimization : 2
[[-122.56446965 45.52319715]
[-122.44609275 45.4903825 ]]
sseSplit, and notSplit: [[510.19541615]] [[2191.82442752]]
optimization : 1
[[-122.64765795 45.58320219]
[-122.66527787 45.49812035]]
optimization : 2
[[-122.70933643 45.58970071]
[-122.69249128 45.48926878]]
optimization : 3
[[-122.72072414 45.59011757]
[-122.69000022 45.48917759]]
sseSplit, and notSplit: [[1435.4378487]] [[851.43888858]]
the bestCentToSplit is: 1
the len of bestClustAss is: 39
optimization : 1
[[-122.53738795 45.5278069 ]
[-122.46545405 45.4449091 ]]
optimization : 2
[[-122.55924018 45.52238271]
[-122.4009285 45.46897 ]]
sseSplit, and notSplit: [[501.32878822]] [[1435.4378487]]
optimization : 1
[[-122.83442992 45.61641997]
[-122.72579569 45.60734039]]
optimization : 2
[[-122.842918 45.646831 ]
[-122.7003585 45.58066533]]
sseSplit, and notSplit: [[48.18024019]] [[2086.91919055]]
optimization : 1
[[-122.72808665 45.40453014]
[-122.7648941 45.51455067]]
optimization : 2
[[-122.69274678 45.43529156]
[-122.68892548 45.51026343]]
sseSplit, and notSplit: [[785.31681488]] [[1051.39643531]]
the bestCentToSplit is: 2
the len of bestClustAss is: 32
optimization : 1
[[-122.42100615 45.44942653]
[-122.54308487 45.53971847]]
optimization : 2
[[-122.4009285 45.46897 ]
[-122.55924018 45.52238271]]
sseSplit, and notSplit: [[501.32878822]] [[985.2743616]]
optimization : 1
[[-122.84118051 45.59449786]
[-122.73809626 45.61741651]]
optimization : 2
[[-122.842918 45.646831 ]
[-122.7003585 45.58066533]]
sseSplit, and notSplit: [[48.18024019]] [[1636.75570346]]
optimization : 1
[[-122.64612316 45.40632725]
[-122.64857012 45.45925123]]
optimization : 2
[[-122.6931845 45.408653 ]
[-122.6923966 45.4566024]]
sseSplit, and notSplit: [[174.50100379]] [[1599.06740886]]
optimization : 1
[[-122.77936513 45.49179874]
[-122.78017202 45.51395644]]
optimization : 2
[[-122.7111539 45.4934771 ]
[-122.67182669 45.523176 ]]
optimization : 3
[[-122.78288433 45.4942305 ]
[-122.65576353 45.51592212]]
sseSplit, and notSplit: [[86.61811321]] [[1289.04227664]]
the bestCentToSplit is: 3
the len of bestClustAss is: 23
4、小结
- 聚类是一种无监督的学习方法。无监督学习是指事先并不知道要寻找的内容,即没有目标变量,或者说没有显著的标签。聚类将数据点归到多个簇中,其中相似数据点处于同一簇,而不同相似数据点处于不同簇中。聚类中可以使用多种不同的方法来计算相似度。
- k-均值聚类的优点是容易实现,缺点是容易受到初始簇质心的影响,可能收敛到局部最小值,在大规模数据集上收敛较慢。适用于数据类型,数值型数据
- 二分k-均值算法首先将所有点作为一个簇,然后使用k-均值算法(k=2)对其划分。下一次迭代时,选择最大误差的簇进行划分。该过程重复直到k个簇创建成功为止。二分k-均值的聚类效果要好于k-均值算法。
K-均值算法以及变形的K-均值算法并非仅有的聚类算法,另外称为层次聚类的方法也被广泛应用——Apriori算法。
该算法尝试在数据集中寻找关联规则,后续将会继续学习。
参考资料:
《机器学习实战》