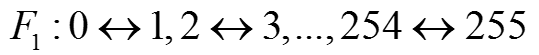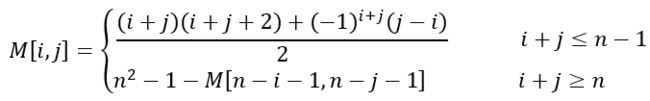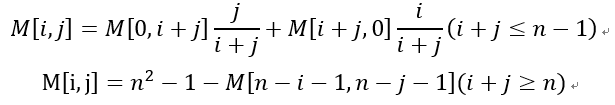图片图层隐写_图片隐写及隐写分析
两句闲话
老师在课上讲了许多图片隐写和隐写分析的方法,在这里我整合一下,并对部分进行代码实现。
LSB隐写
LSB隐写是最基础、最简单的隐写方法,具有容量大、嵌入速度快、对载体图像质量影响小的特点。
LSB的大意就是最低比特位隐写。我们将深度为8的BMP图像,分为8个二值平面(位平面),我们将待嵌入的信息(info)直接写到最低的位平面上。换句话说,如果秘密信息与最低比特位相同,则不改动;如果秘密信息与最低比特位不同,则使用秘密信息值代替最低比特位。
具体实现如下
from PIL import Image
import math
class LSB:
def __init__(self):
self.im=None
def load_bmp(self,bmp_file):
self.im=Image.open(bmp_file)
self.w,self.h=self.im.size
self.available_info_len=self.w*self.h # 不是绝对可靠的
print ("Load>> 可嵌入",self.available_info_len,"bits的信息")
def write(self,info):
"""先嵌入信息的长度,然后嵌入信息"""
info=self._set_info_len(info)
info_len=len(info)
info_index=0
im_index=0
while True:
if info_index>=info_len:
break
data=info[info_index]
x,y=self._get_xy(im_index)
self._write(x,y,data)
info_index+=1
im_index+=1
def save(self,filename):
self.im.save(filename)
def read(self):
"""先读出信息的长度,然后读出信息"""
_len,im_index=self._get_info_len()
info=[]
for i in range(im_index,im_index+_len):
x,y=self._get_xy(i)
data=self._read(x,y)
info.append(data)
return info
#===============================================================#
def _get_xy(self,l):
return l%self.w,int(l/self.w)
def _set_info_len(self,info):
l=int(math.log(self.available_info_len,2))+1
info_len=[0]*l
_len=len(info)
info_len[-len(bin(_len))+2:]=[int(i) for i in bin(_len)[2:]]
return info_len+info
def _get_info_len(self):
l=int(math.log(self.w*self.h,2))+1
len_list=[]
for i in range(l):
x,y=self._get_xy(i)
_d=self._read(x,y)
len_list.append(str(_d))
_len=''.join(len_list)
_len=int(_len,2)
return _len,l
def _write(self,x,y,data):
origin=self.im.getpixel((x,y))
lower_bit=origin%2
if lower_bit==data:
pass
elif (lower_bit,data) == (0,1):
self.im.putpixel((x,y),origin+1)
elif (lower_bit,data) == (1,0):
self.im.putpixel((x,y),origin-1)
def _read(self,x,y):
data=self.im.getpixel((x,y))
return data%2
if __name__=="__main__":
lsb=LSB()
# 写
lsb.load_bmp('test.bmp')
info1=[0,1,0,1,1,0,1,0]
lsb.write(info1)
lsb.save('lsb.bmp')
# 读
lsb.load_bmp('lsb.bmp')
info2=lsb.read()
print (info2)
在这里,我们定义几个指标来评价隐写算法。
假设,某灰度图像的大小为$M\times N$,深度为8。
嵌入容量$M\times N$bit。
嵌入率$\frac{嵌入容量}{总容量}$,LSB的嵌入率为$\frac{1}{8}=12.5\%$。
MSE mean square error,平均方根误差,$MSE=\frac{\sum^{M}_{m=1}\sum^{N}_{n-1}d(m,n)^2}{M \times N}$,这里的$d(m,n)$指的是,原图像和修改后的图像在$(m,n)$位置上的像素点之差。
PSNR peak signal-to-noise ratio,峰值信噪比,$PSNR=-10log\{\frac{MSE}{255^2MN}\}$。
更多的评价方法还有,VQM(vedio quality measurement), SSIM(structural similarity index)等。
面向JPEG的图像隐写(1):Jsteg隐写
关于JPEG格式,可以看看这篇博客 JPEG图像压缩算法流程详解。JPEG压缩中,最主要的就是DCT变换。
Jsteg隐写是将秘密信息嵌入在量化后的DCT系数的LSB上,但原始值为-1,0,+1的DCT系数除外。此外,由于量化后的DCT系数中有负数,编程的时候需要格外注意以下。
具体实现如下
import math
class Jsteg:
def __init__(self):
self.sequence_after_dct=None
def set_sequence_after_dct(self,sequence_after_dct):
self.sequence_after_dct=sequence_after_dct
self.available_info_len=len([i for i in self.sequence_after_dct if i not in (-1,1,0)]) # 不是绝对可靠的
print ("Load>> 可嵌入",self.available_info_len,'bits')
def get_sequence_after_dct(self):
return self.sequence_after_dct
def write(self,info):
"""先嵌入信息的长度,然后嵌入信息"""
info=self._set_info_len(info)
info_len=len(info)
info_index=0
im_index=0
while True:
if info_index>=info_len:
break
data=info[info_index]
if self._write(im_index,data):
info_index+=1
im_index+=1
def read(self):
"""先读出信息的长度,然后读出信息"""
_len,sequence_index=self._get_info_len()
info=[]
info_index=0
while True:
if info_index>=_len:
break
data=self._read(sequence_index)
if data!=None:
info.append(data)
info_index+=1
sequence_index+=1
return info
#===============================================================#
def _set_info_len(self,info):
l=int(math.log(self.available_info_len,2))+1
info_len=[0]*l
_len=len(info)
info_len[-len(bin(_len))+2:]=[int(i) for i in bin(_len)[2:]]
return info_len+info
def _get_info_len(self):
l=int(math.log(self.available_info_len,2))+1
len_list=[]
_l_index=0
_seq_index=0
while True:
if _l_index>=l:
break
_d=self._read(_seq_index)
if _d!=None:
len_list.append(str(_d))
_l_index+=1
_seq_index+=1
_len=''.join(len_list)
_len=int(_len,2)
return _len,_seq_index
def _write(self,index,data):
origin=self.sequence_after_dct[index]
if origin in (-1,1,0):
return False
lower_bit=origin%2
if lower_bit==data:
pass
elif origin>0:
if (lower_bit,data) == (0,1):
self.sequence_after_dct[index]=origin+1
elif (lower_bit,data) == (1,0):
self.sequence_after_dct[index]=origin-1
elif origin<0:
if (lower_bit,data) == (0,1):
self.sequence_after_dct[index]=origin-1
elif (lower_bit,data) == (1,0):
self.sequence_after_dct[index]=origin+1
return True
def _read(self,index):
if self.sequence_after_dct[index] not in (-1,1,0):
return self.sequence_after_dct[index]%2
else:
return None
if __name__=="__main__":
jsteg=Jsteg()
# 写
sequence_after_dct=[-1,0,1]*100+[i for i in range(-7,500)]
jsteg.set_sequence_after_dct(sequence_after_dct)
info1=[0,1,0,1,1,0,1,0]
jsteg.write(info1)
sequence_after_dct2=jsteg.get_sequence_after_dct()
# 读
jsteg.set_sequence_after_dct(sequence_after_dct2)
info2=jsteg.read()
print (info2)
在上面,我们实现了对量化后的DCT系数的隐写。至于如何得到DCT系数,可以使用opencv中的函数,如下
import cv2
import numpy as np
def dct(m):
m = np.float32(m)/255.0
return cv2.dct(m)*255
面向JPEG的图像隐写(2):F3隐写
在Jsetg隐写方法中,原始值为-1,0,+1的DCT系数,不负载秘密信息,但是量化后的DCT系数中却有大量的-1,0,+1(以0居多),这说明Jsetg的嵌入率会很小。为了改善这一状况,人们提出了F3隐写。
F3则对原始值为+1和-1的DCT系数,进行了利用。F3隐写的规则如下
(1) 每个非0的DCT数据用于隐藏1比特秘密信息,为0的DCT系数不负载秘密信息。
(2) 如果秘密信息与DCT的LSB相同,便不作改动;如果不同,将DCT系数的绝对值减小1,符号不变。
(3) 当原始值为+1或-1且预嵌入秘密信息为0时,将这个位置归0并视为无效,在下一个DCT系数上重新嵌入。
我们可以看出来,F3对Jsteg的改动并不大。因此,在代码实现上,我们可以复用Jsteg的代码,具体如下
from jsteg import Jsteg
import math
class F3(Jsteg):
def __init__(self):
Jsteg.__init__(self)
def set_sequence_after_dct(self,sequence_after_dct):
self.sequence_after_dct=sequence_after_dct
sum_len=len(self.sequence_after_dct)
zero_len=len([i for i in self.sequence_after_dct if i==0])
one_len=len([i for i in self.sequence_after_dct if i in (-1,1)])
self.available_info_len=sum_len-zero_len-one_len # 不是特别可靠
print ("Load>> 大约可嵌入",sum_len-zero_len-int(one_len/2),'bits')
print ("Load>> 最少可嵌入",self.available_info_len,'bits\n')
def _write(self,index,data):
origin=self.sequence_after_dct[index]
if origin == 0:
return False
elif origin in (-1,1) and data==0:
self.sequence_after_dct[index]=0
return False
lower_bit=origin%2
if lower_bit==data:
pass
elif origin>0:
self.sequence_after_dct[index]=origin-1
elif origin<0:
self.sequence_after_dct[index]=origin+1
return True
def _read(self,index):
if self.sequence_after_dct[index] != 0:
return self.sequence_after_dct[index]%2
else:
return None
if __name__=="__main__":
f3=F3()
# 写
sequence_after_dct=[-1,0,1]*100+[i for i in range(-7,500)]
f3.set_sequence_after_dct(sequence_after_dct)
info1=[0,1,0,1,1,0,1,0]
f3.write(info1)
sequence_after_dct2=f3.get_sequence_after_dct()
# 读
f3.set_sequence_after_dct(sequence_after_dct2)
info2=f3.read()
print (info2)
可嵌入容量的计算
这里需要说的是,由于F3隐写特殊的规则,我们无法精确得到可嵌入的信息的容量,我们只能得到最小值,即原始值为非0,-1,+1的像素点的数量。但是,我们可以得到一个数学期望。但是这个期望等于多少呢?我们来算一下。
为了严谨性,我们先列出几条假设:
(1) 待嵌入信息为01串。在此01串中,0和1随机均匀分布,且0和1出现的概率分别为50%。
(2) 假设系数表中不同系数的出现是随机的,我们忽略它们出现的次序,如非0、-1、+1的出现总是相邻的。
此外,我们设量化后的DCT系数表中,0的概率为$p_0$,-1和1的概率为$p_1$,其他数字出现的概率为$p_2$;DCT系数表的长度为n;待嵌入的01串的长度为m。
则假设我们要嵌入0,我们需要DCT系数的个数为$\frac{1}{p_2}$;假设我们要嵌入1,我们需要DCT系数的个数是$\frac{1}{p_1+p_2}$。由于01出现的概率分别为50%,因此我们嵌入一位所需要的DCT系数的个数为$\frac{\frac{1}{p_2}+\frac{1}{p_1+p_2}}{2}=\frac{p_1+2p_2}{2p_2(p_1+p_2)}$,因此m与n的关系为$m=\frac{n}{\frac{p_1+2p_2}{2p_2(p_1+p_2)}}=\frac{2np_2(p_1+p_2)}{p_1+2p_2}$。
在实际实施的,我们统计0的数量$n_0$,-1和1的数量$n_1$,其他数字出现的概率为$n_2$,于是$m=\frac{2n_2(n_1+n_2)}{n_1+2n_2}$。
面向JPEG的图像隐写(3):F5隐写
调色板隐写(EZStego隐写)
首先,介绍调色板图像。
调色板图像调色板图像是互联网上常见的一种图像格式,其中含有一个不超过256种颜色的调色板,并定义了每种颜色对应的R,G,B各颜色分量值,图像内容中的每个像素是不超过8比特信息的一个索引值,其指向的调色板中的对应颜色即该像素中的真实颜色。常见的调色板图像格式是GIF,PNG。
EZStego隐写
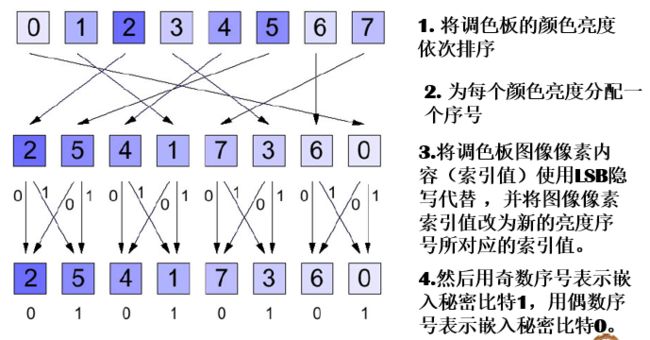
(1) 将调色板的颜色亮度依次排序,其中颜色的亮度由不同的颜色分量线性叠加而成,其表达式为$Y=0.299R+0.587G+0.114B$。
(2) 为每个颜色分配一个亮度序号。
(3) 将调色板图像像素内容使用LSB隐写代替,并将图像像素索引值改为新的亮度序号所对用的索引值。
(4) 用奇数序号表示嵌入秘密比特1,用偶数序号表示嵌入秘密比特0。
python代码
from PIL import Image
import numpy as np
import math
"""
假设调色板索引为
0 1 2 3 4 5 6 7
假设亮度序号(Y_index)为
index:0 1 2 3 4 5 6 7
2 5 4 1 7 3 6 0
则
# Y_index_inverse
index:0 1 2 3 4 5 6 7
7 3 0 5 2 1 6 4
# 例子
载体 [3 0 6 4] ; 待嵌入信息 0110
嵌入:[3 0 6 4]=>[5 7 6 2]=>(by 0110) [4 7 7 2]=>[7 0 0 4]
结果:[3 0 6 4]=>(by 0110)=>[7 0 0 4]
提取:[7 0 0 4]=>[4 7 7 2]=>0110
"""
class GIF_Steg:
def __init__(self):
self.im=None
def load_gif(self,gif_file):
self.im=Image.open(gif_file)
self._load_palette()
self._sort_palette()
self._load_palette_data()
self.available_info_len=len(self.palette_data)
def write(self,info):
info=self._set_info_len(info)
self.palette_data=self._write(self.palette_data,info)
def read(self):
_len,im_index=self._get_info_len()
info=self._read(self.palette_data[im_index:im_index+_len])
return info
def save(self,filename):
self.im.save(filename)
#==========================================#
def _load_palette(self):
self.palette=[]
palette=self.im.palette.palette
for i in range(int(len(palette)/3)):
self.palette.append((palette[3*i],palette[3*i+1],palette[3*i+2]))
def _sort_palette(self):
f=lambda t:0.299*t[0]+0.587*t[1]+0.114*t[2]
Y=[f(t) for t in self.palette]
self.Y_index=np.argsort(Y)
self.Y_index_inverse=[0]*256
for i in range(len(self.Y_index)):
self.Y_index_inverse[self.Y_index[i]]=i
def _load_palette_data(self):
self.palette_data=self.im.getpalette()
def _set_info_len(self,info):
l=int(math.log(self.available_info_len,2))+1
info_len=[0]*l
_len=len(info)
info_len[-len(bin(_len))+2:]=[int(i) for i in bin(_len)[2:]]
return info_len+info
def _get_info_len(self):
l=int(math.log(self.available_info_len,2))+1
len_list=[]
for i in range(l):
_d=self._get_lsb(self.palette_data[i])
len_list.append(str(_d))
_len=''.join(len_list)
_len=int(_len,2)
return _len,l
def _write(self,palette_data,info):
for i in range(len(info)):
Y_index=self.Y_index_inverse[palette_data[i]]
lower_bit=Y_index%2
if lower_bit==info[i]:
pass
elif (lower_bit,info[i])==(0,1):
palette_data[i]=self.Y_index[Y_index+1]
elif (lower_bit,info[i])==(1,0):
palette_data[i]=self.Y_index[Y_index-1]
return palette_data
def _read(self,palette_data):
info=[]
for i in range(len(palette_data)):
info.append(self._get_lsb(palette_data[i]))
return info
def _get_lsb(self,_palette_data):
return self.Y_index_inverse[_palette_data]%2
if __name__=="__main__":
gs=GIF_Steg()
gs.load_gif('4.1.05.gif')
gs.write([0,1,1,0,0,1,0,0,0,0,0])
print (gs.read())
BPCS隐写
PVD隐写
卡方分析
RS分析
RS隐写分析的原理,在百度文库的这个ppt上说的比较清楚。
首先介绍像素翻转$F_1,F_0,F_{-1}$。$F_1$是像素值$2n$与$2n+1$之间的变换,$F_{-1}$是像素值$2n-1$与$2n$之间的变换,$F_0$则是像素值不发生改变。即
设一掩码算子$m=(m_1,m_2,\cdots,m_n),(m_i\in {0,1})$。现在定义$F_m$与$F_{-m}$。对于长度为n的像素值的序列$G$,$F_m(G)=(F_{m_1}(G[1]),\cdots,F_{m_i}(G[i]),\cdots,F_{m_n}(G[n]))$。相应地,$F_{-m}(G)=(F_{-m_1}(G[1]),\cdots,F_{-m_i}(G[i]),\cdots,F_{-m_n}(G[n]))$。
现在,我们定义像素相关性,设$G$长度为n的像素值的序列,$G=(x_1,x_2,\cdots,x_n)$。则$序列G$像素相关性$f(G)=\sum_{i=1}^{n-1}{|x_{i+1}-x_i|}$。
大量实验表明,当一个像素值序列经历$F_m$或$F_{-m}$之后,像素相关性的变化会随着图片中嵌入秘密信息的数量会呈现出一些规律。
我们将图片分块,每一块通过Z字形扫描变成一段序列,这样我们就得到了多个像素点序列。对所有序列使用非负翻转$F_m$和$F_{-m}$翻转,像素相关性增加或减少的比例,我们分别设为$R_m,S_m,R_{-m},S_{-m}$。即
$R_m$ 为$F_m$作用下像素相关性增加占所有像素组的比例
$R_{-m}$ 为$F_{-m}$作用下像素相关性增加占所有像素组的比例
$S_m$ 为$F_{m}$作用下像素相关性减少占所有像素组的比例
$S_{-m}$ 为$F_{-m}$作用下像素相关性减少占所有像素组的比例
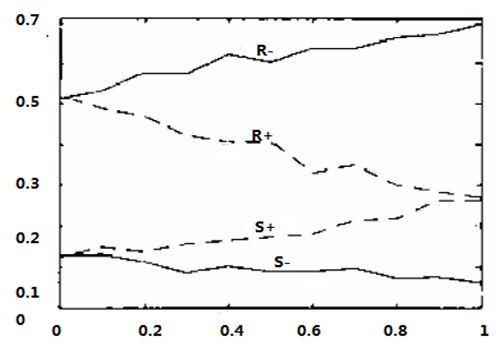
假设一图像嵌入了秘密信息,嵌入率为$\alpha$,即原图中比例为$\frac{\alpha}{2}$的像素值发生了改变,那么$\alpha$与$R_m,R_{-m},S_m,S_{-m}$的关系如下图(大量实验的结果)
下面的代码能够得到上图。至于如何根据一张隐写的图片,得到图片中是否经过隐写,以及得到嵌入率,这就是另一个问题。这个问题比较复杂,上面给的ppt中,有介绍。
import sys
import math
import numpy as np
from PIL import Image
import random
def get_index_matrix(n):
"""
得到n阶zigzag扫描矩阵
"""
I=np.array(range(n))
J=I.reshape(-1,n).T
M=((I+J)*(I+J+2)+(I-J)*(-1)**(I+J))/2
one_tril=np.triu(np.ones((n,n)))[:,::-1]
M=M*one_tril
M=M+(n**2-1-M)[::-1,::-1]*(1-one_tril)
return M.astype(int)
def get_mask(n):
"""
得到掩码m
"""
return np.random.randint(low=0,high=2,size=n)
class RS:
def __init__(self):
self._region_length=8
self.set_parameter()
def load_bmp(self,bmp_file):
"""
加载bmp文件
"""
self.im=Image.open(bmp_file)
self.w,self.h=self.im.size
print (">> 加载图片,图片尺寸:",self.w,"x",self.h)
def set_parameter(self,_region_length=8):
self._region_length=_region_length
self._zigzag_index_matrix=get_index_matrix(_region_length)
self._m=get_mask(_region_length**2)
def analyse(self):
_rs1=[0,0,0,0] # [Rm,Sm,R-m,S-m]
_rs2=[0,0,0,0] # [Rm,Sm,R-m,S-m]
self._RS_build(_rs1,_rs2)
_sum=math.ceil(self.w/self._region_length)*math.ceil(self.h/self._region_length)
_rs1=[i/_sum for i in _rs1]
_rs2=[i/_sum for i in _rs2]
res=self._get_insert_rate(_rs1,_rs2)
print (res)
############## unfinished
def get_RS_map(self,n=100):
"""
得到点集 (嵌入率-RS)
"""
res=[]
for i in range(n+1):
_rs=[0,0,0,0]
rate=i/n
self._RS_build_by_rate(_rs,rate)
print (rate,_rs)
res.append((rate,_rs))
return res
######################################################
def _RS_build(self,_rs1,_rs2):
row=math.ceil(self.w/self._region_length)
column=math.ceil(self.h/self._region_length)
for i in range(row):
for j in range(column):
# 从图像取出一块区域,进行zigzag扫描
box=np.array([i,j,i+1,j+1])*self._region_length
region=self.im.crop(box)
region=np.array(region)
sequence=self._zigzagScan(region)
# 对RS进行统计
self._rs_build(sequence,_rs1)
# 进行正翻转,得到修改率为1-a/2的序列,对RS进行统计
sequence=self._Fm(sequence,np.ones(self._region_length**2).astype(int))
self._rs_build(sequence,_rs2)
def _RS_build_by_rate(self,_rs,rate):
"""
根据嵌入率得到RS的值
"""
row=math.ceil(self.w/self._region_length)
column=math.ceil(self.h/self._region_length)
for i in range(row):
for j in range(column):
# 从图像取出一块区域,进行zigzag扫描
box=np.array([i,j,i+1,j+1])*self._region_length
region=self.im.crop(box)
region=np.array(region)
sequence=self._zigzagScan(region)
# 以概率rate,嵌入01
sequence=self._random_inject(sequence,rate)
# 对RS进行统计
self._rs_build(sequence,_rs)
def _zigzagScan(self,m):
"""
Z字形扫描
"""
sequence = np.zeros(self._region_length**2,).astype(int)
for i in range(self._region_length):
for j in range(self._region_length):
index = self._zigzag_index_matrix[i][j]
sequence[index] = m[i,j]
return sequence
def _random_inject(self,sequence,rate):
"""
随机嵌入秘密信息,嵌入率rate
"""
m=np.ceil(np.random.random(self._region_length**2)-rate/2).astype(int)
return self._Fm(sequence,m)
def _rs_build(self,sequence,_rs):
"""
根据sequence修改RS的值
"""
r1=self._get_relativity(sequence)
r2=self._get_relativity(self._Fm(sequence, self._m))
r3=self._get_relativity(self._Fm(sequence,-self._m))
if r1
_rs[0]+=1
elif r1>r2:
_rs[1]+=1
if r1
_rs[2]+=1
elif r1>r3:
_rs[3]+=1
def _get_relativity(self,sequence):
"""
得到像素相关性
"""
a=np.abs(np.array(sequence)[1:]-np.array(sequence)[:1])
return np.sum(a)
def _Fm(self,sequence,m):
"""
由m定义的翻转
"""
# [0,1,-1]
# (x+0)^0-0,(x+0)^1-0,(x-1)^1+1
# ((x+a)^b)-a
a=np.floor(m/2).astype(int)
b=np.abs(m).astype(int)
return ((sequence+a)^b)-a
if __name__=="__main__":
rs=RS()
rs.load_bmp("../_data/misc/5.3.01.tiff")
# rs.analyse()
res=rs.get_RS_map()
import matplotlib.pyplot as plt
for i in range(4):
plt.plot([p[0] for p in res],[p[1][i] for p in res],'ro')
plt.show()
对于上面的代码,有三点需要说明。
1.如何实现zigzag扫描
在代码中,我们是通过一个索引矩阵来实现zigzag扫描的,其中,八阶的索引矩阵如下
那么,对于其他阶数的索引矩阵,怎么得出呢?设M为n阶索引矩阵,则有如下的关系
那这个是怎么得到的呢?当然是自己推啦。这里给出推导思路,首先求出$M[0,j]$和$M[i,0]$的关系式,然后利用下面两个关系式得到$M[i,j]$的表达式
至于有没有必要,费劲波折得到这个,那我就不知道了。
2.如何快速实现翻转
使用异或,我们能实现快速的翻转。$F_0(x)=x\oplus 0,\\F_1(x)=x\oplus 1,\\F_{-1}(x)=((x-1)\oplus 1)+1$。\\为了快速地实现$F_m$,我们定义$F(a,b,x)=((x-a)\oplus b)+a$。于是$F_0(x)=F(0,0,x),F_1(x)=F(0,1,x),F_{-1}(x)=F(1,1,x)$。进一步,对于翻转$F_i$,令$a=\lfloor i/2\rfloor,b=|i|$,于是$F_i(x)=F(a,b,x)$。
这样有什么用呢?答案就是大大方便了矩阵运算。不过,应该有比这更快的计算方法。这里不做研究。
3.敏感性分析
m怎么确定?按照n*n分块,n怎么确定?
在代码中,我是随机的生成一个含0和1比例各50%的一个向量。为什么是50%呢?我发现对于有些图像设为50%会得到比较好的结果(图像比较合乎规律),有些图像比例应该设为90%才会得到比较好的结果。
n的大小又会怎么影响结果?
这里的水,就比较深了。
F3隐写分析