形式化方法
什么是形式化方法?
PS:软件工程作业,老师要求自己去阅读和了解形式化方法是什么,自己查阅了一下,感觉实在是难懂......
正文:
1 形式化方法基本概念
形式化方法是基于严格数学基础, 对计算机软(硬)件系统进行形式规约、开发和验证的技术.其中, 形式规约使用形式语言构建所开发的软件系统的规约, 它们对应于软件生命周期不同阶段的制品, 刻画系统不同抽象层次的模型和性质, 例如需求模型、设计模型甚至代码和代码的执行模型等.形式验证是证明不同形式规约之间的逻辑关系, 这些逻辑关系反映了在软件开发不同阶段软件制品之间的需要满足的各类正确性需求.例如, 形式验证给出“系统设计模型满足若干特定性质”的证明构造.在形式规约和验证的基础上, 形式化开发主要是构造、证明形式规约之间的等价转换和精化关系, 以系统的形式模型为指导, 逐步精化, 开发出满足需要的系统, 也称为构造即正确(correct by construction)的开发.
形式化方法与其他软件开发方法[4]的主要区别在于:其描述软件及其性质的语言是无歧义的, 构造和验证软件的方法是严格的.在软件工程中, 形式化方法提供了工程化系统设计的一种比较透彻的思维方式, 可以很好地支持抽象模型建立、系统精化、模型和证明重用; 形式化开发过程具有很好的可重复性, 相应的软件制品模型也具有较强的可分析性和可验证性.因而, 形式化方法可以有效地提高和保障系统的可信性.
形式化方法与计算机科学理论密切相关, 其发展与程序设计语言和程序理论的发展息息相连.作为一个学科方向, 它研究形式化方法的数学基础、形式系统的表达能力、形式系统的推理系统及其可靠性和完备性, 以及在计算系统开发和生命周期各个阶段的理论、方法、技术、工具和应用方式等.
1.1 历史回顾
形式化方法的发展已有较长的历史, 人们主要从两个角度出发推动形式化方法的提出和早期发展, 即, 为程序设计提供数学基础的理论研究角度以及为软件开发提供严格质量保证的软件工程角度.早在1949年, Turing的论文“Checking a large routine”即讨论了程序的正确性问题[5].1962年, McCarthy在IFIP上做了题为“通往计算的数学科学”的演讲[6], 系统论述了程序语言的形式语义和程序设计理论重要性, 直接触发了形式语义研究. 1968年在德国Garmisch召开的NATO软件工程会议, 从提高软件质量和生产率的软件工程角度出发, 提出了要建立软件开发和生产的数学基础; 进一步地, 软件的正确性问题和概念成为1969年NATO软件工程会议的主题之一.形式化方法在这种历史背景下成为程序设计和软件工程基础的重要组成部分, 先后出现了一批有重要影响的工作.表 1给出了部分图灵奖获奖者在形式化方法方面的研究工作.
 |
Table 1 Examples of formal methods researches by Turing Award Laureates表 1 部分图灵奖获得者在形式化方法方面的研究 |
1.1.1 围绕形式语言和形式语义学的基础研究(1930年~至今)
形式语言是由符号化字母表以及递归的语法规则完全定义和生成所有表达式或语句的语言.形式逻辑的语言都是形式语言, 如命题逻辑、谓词逻辑和布尔代数.20世纪30年代, Church用形式语言定义研究计算和算法, 提出了一种计算模型Lambda演算[7, 8], 后来成为函数式程序设计语言、类型论和操作语义的理论基础.事实上, Lambda演算本身可以看作是一种程序语言.在20世纪50年代末, 高级程序设计语言的定义开始了关于计算的形式系统的研究, 产生了Backus-Naur Forms(BNF范式)并用于定义ALGOL60, 形成了语言的递归抽象.形式语言不仅在语言的定义中得到了应用, 在系统软件开发中也发挥了作用, 例如, UNIX中的yacc和grep的开发[9].在形式语言定义的同时, 如何定义程序的含义成为关注的焦点[10], 形式语义学的研究逐渐形成了四大体系:操作语义、指称语义、代数语义和公理语义.在定义ALGOL68的语义时, 首次使用了“操作语义”这个术语, 而McCarthy已在1960年用Lambda演算定义了LISP的语义[11].形式语言理论和形式语义学为形式化方法奠定了基础, 不仅用来定义程序设计语言, 形式系统还用来严格定义规约语言的基础, 建立了形式规约语言或形式化建模语言.20世纪60年代, Petri提出了Petri Net作为分布式系统的数学化建模语言[12].面向并发系统, Hoare提出了通信顺序进程CSP[13, 14], Milner提出了通信系统演算CCS[15, 16], Hennessy和Lin提出了消息传送进程的符号互模拟理论[17].随着软件形态的不断变化, 形式化建模语言也不断发展.例如, 针对反应式系统, Pnueli在1977年引入了线性时序逻辑LTL[18], Clarke和Emerson在1981年建立了计算树逻辑CTL[19]; 在反应式系统描述的基础上, 发展了面向实时系统的TPTL[20]、Timed Automata[21]、Timed Regular Expressions[22]和Timed CSP[23]以及Timed CCS[24], 还出现了硬件描述语言、体系结构描述语言、通信控制建模仿真语言等.
1.1.2 围绕形式规约和开发的方法学研究(1970年~至今)
直接使用程序设计语言及其语义难以描述和证明软件从需求文档到程序代码的开发过程各阶段创建的不同抽象层次的制品及其正确性, 人们开始研究高层抽象的形式规约语言的设计, 形成了以形式规约语言为基础的形式化开发方法.例如VDM[25-27]、Z[28]、Event-B[29]、RAISE[30, 31]、CafeOBJ[32]、TLA+[33]、rCOS[34]、SOFL[35]等等.形式化开发利用形式规约语言对软件建模并描述其所期望的软件性质, 提供指导开发人员进行精化的方法, 进行形式规约之间(部分的)一致性检查和证明.基于不同的开发方法, 形式规约可以自顶向下逐步精化形成开发的规约序列, 在足够的实现细节完成后, 可以通过代码自动生成得到程序.例如, VDM的精化有数据具体化(data reification)和操作分解(operation decomposition)等.形式化方法逐步建立了工具集, 以支持形式规约的性质分析和证明, 例如Z/EVES[36]、Event-B/Rodin[37].1970年代后, 软件工程界认识到了数学可以为保证程序正确性提供技术基础, 形式化方法(formal methods)一词开始传播开来.1980代初, 唐稚松提出以时序逻辑作为软件开发过程的统一基础, 并着手建立XYZ系统[38].在1980年代到90年代, 形式化方法得到了重视, 特别是欧盟大力支持了形式化开发方法的研究.例如Concur、ProCoS、REACT等.人们希望能够利用形式化方法高效、高质量地开发软件, 这一方面有力地促进了形式化方法和技术的发展; 另一方面, 由于应用规模较小, 效果证据不足, 应用方式不明确, 工业界对形式化方法的看法出现了争议.在形式规约和开发的方法学基础方面, Goguen和Burstall提出了机构(institution)的抽象模型理论, 用以建立语言语法驱动的、不同形式逻辑基础上的各种形式化方法的理论统一以及技术和工具集成与和谐使用[39]; Hoare和何积丰提出了统一程序设计理论框架UTP, 提供了在一种程序(如顺序程序)语义模型理论基础上构建扩展程序(如并发)的语义理论, 从而保证原来的理论在扩展的理论中重用, 并同时建立了操作语义、指称语义、公理语义和代数语义的互联统一[40].
1.1.3 围绕形式验证技术的工程化研究(1980年~至今)
建立了形式规约之后, 如何从形式规约开发得到正确的系统成为关键.形式验证, 包括如何证明不同抽象层次的规约间等价或者满足精化关系、如何验证形式规约(所要求的性质)及其模型之间的满足关系, 是形式化方法保证软件开发正确性必须解决的科学问题和实际应用问题.形式验证理论涉及了数理逻辑的传统基础问题.在研究验证自动化过程中, 发现了相关大量的不可判定问题、NP完全问题以及状态爆炸等否定性的结果.否定性的结果同时推动了各种可组合的规约证明技术、抽象解释技术以及提高实现效率的数据结构(如BDD).这些研究同时促进了形式化技术与传统测试和仿真技术的结合, 形成了新的基于形式化的测试和仿真技术.这些技术将重点放在软件的缺陷检验和调试上, 以发现错误为首要目的[3], 出现了形式验证及其工程化技术和工具, 包括以SAT/SMT为代表的约束求解、基于交互式辅助定理证明工具的机械化验证、以模型检验为代表的自动分析与验证.工具的自动化水平和可扩展能力得到了显著的提高, 如SAT/SMT求解器Chaff[41]、Z3[42]、CVC4[43], 定理证明环境ACL2[44]、Isabelle/HOL[45]、Coq[46]和PVS[47], 模型检验工具SMV[48]、SPIN[49]、UPPAAL[50], PRISM[51]、PAT[52]等等.形式验证在硬件验证中获得了巨大的成功, 也不断地进入嵌入式软件、安全攸关软件等高安全等级软件的开发.Pnueli在他的图灵奖演说中称, 验证工程(verification engineering)是未来的职业[53].
1.1.4 以可验证软件为目标的多学科交叉研究(2000年~至今)
1999年, 在关于计算机科学技术面临的巨大挑战的讨论中, Hoare提出了验证编译器(verifying compiler)倡议(后称为verified software).经过几年的调研和准备, 2005年召开了第1届VSTTE(verified software:Theories, tools, experiments)会议.来自世界各地的专家讨论了形式规约、构建和验证高质量软件的方法, 形成了可验证软件计划, 希望[54]:(1)建立能够构建实际可靠的程序的设计理论; (2)建立一组支持上述理论的自动化工具集, 并且能扩展至具有工业化能力; (3)建立已验证的程序库, 能够在实际系统中替代未验证的程序, 并能以可验证的状态持续演化.2007年, 我国国家自然科学基金委也开展了“可信软件基础研究”重大研究计划[55-57], 形式化方法作为其中的重要途径来提高软件的可信性.经过10余年的努力, 形式化方法进入了硬件设计的标准流程, 也出现了验证过的编译器[58]和微内核操作系统[59].人们普遍认可了形式化方法对于深刻认识计算系统和提高软件质量的贡献.美国NITRD在计算使能的网络化物理系统(CNPS)、网络空间安全和隐私(CSP)、软件生产力、可持续和质量(SPSQ)等多个领域(PCA)突出了形式化方法的位置, NSF连续资助了形式化方法领域的大规模探索项目CMACS[60]、EXCAPE[61]、DeepSpec[62]等.DARPA的项目HACMS[63]利用形式化方法成功地研发了可以免于黑客攻击的无人机操作系统和飞行控制软件.形式化方法在计算机软/硬件开发和质量保证上发挥了重要作用, 与人工智能相结合的程序综合、大数据以及与形式推理相结合的软件自动化重回热点前沿.此外, 形式化方法在网络安全、量子计算、生物计算等方向的交叉应用也受到了广泛关注.
1.2 形式化方法的基本体系
图 1给出了基于形式化方法进行软件开发的基本框架.与基于模型的软件开发类似, 通过需求分析得到初始形式规约Spec1; 然后, 经过逐步求精或者转换, 得到一系列精化后的形式规约(Spec2, …, Specn); 最后, 可转换或综合生成得到系统的程序代码实现.Spec1, ..., Specn都是对系统的抽象(建模), 它们的抽象角度和层次不同.
 |
Fig. 1 Framework of formal (development) methods图 1 形式化方法软件开发框架整体图 |
图 1中还给出了形式规约语法、语义以及形式规约之间的关系.给定形式规约Speci, 由语义函数[[_]]给出其在数学域上的形式语义[[Speci]](即Semanticsi).规约之间的逻辑关系(如精化关系可以描述为逻辑中的蕴含“→”)与相应数学理论(如集合论中的集合包含“⊒”)有对应关系(如, 若Spec2→Spec1, 则[[Spec1]]⊒[[(Spec2)]]).在软件开发中, 规约不必仅用同一种形式语言描述, 不同的规约语言之间的关系可以基于某个统一的形式理论, 例如Institutions[39].
综上所述, 形式化方法是由形式规约语言(包括形式语义与模型理论)、形式规约(包括精化与综合)、形式验证、形式化工具等形成的一个整体.其中, 形式规约语言是基础, 形式化方法中, 软件制品是规约语言编写/变换的形式规约; 形式验证是保证开发正确性的途径, 形式语义与模型理论是联接形式规约和形式验证的数学纽带; 形式化工具是系统设计和开发中高效使用形式化方法的需要和实践.
2 形式规约
形式规约是由形式规约语言严格描述的系统模型或者系统需要满足的性质.前者是模型规约, 后者是性质规约.形式规约是形式化方法的基础[64].在软件分析[2, 3]中, 动态执行测试或验证技术以及动态在线跟踪监控和验证也经常使用形式规约.
本节我们讨论形式规约语言及其语义的定义方法、形式规约和语义模型之间的关系, 并在此基础上介绍形式规约在软件构造中的应用.
2.1 形式规约语言
形式规约语言是指由严格的递归语法规则所定义的语言, 满足语法规则的句子称为合式或良定义规约(well-formed specification).
2.1.1 模型规约语言
模型规约语言利用数学结构描述系统的状态变化或者事件轨迹, 它直接定义所描述系统模型的结构、功能行为甚至非功能行为(如时间).模型规约给出了系统开发过程中不同抽象层次的模型, 有相应的逻辑推理系统支持其分解和组合, 完成不同层次间规约的转换和精化.主要包括如下几类.
(1) 代数规约语言
一个代数规约由一些表述类子(sort)的符号、类子之间的运算符(operation symbol)以及在多类等式逻辑(many-sorted equality logic)中的等式公理组成.代数规约的一个模型就是满足该规约的异构代数.为了语义的唯一性, 一般采取初始代数(initial algebra)为规约的语义.代数规约的优点是具有非常好的数学基础, 任意操作序列的计算结果可以自动得到、自动执行, 例如4GL(fourth generation programming languages).等式逻辑的表述能力有较大局限性, 不能表达一般的程序结构和行为.因此, 后来代数描述中引进了带归纳的一阶逻辑, 同时引进了支持偏函数和子类, 模块化结构和模块组合的架构机制, 形成了一个通用代数规约语言(the common algebraic specification language, 简称CASL)[65].其他的代数规约语言还有OBJ[66]、PLUSS[67]、Larch[68]等.代数规约对程序设计理论和软件工程影响非常广泛, 例如早期的抽象数据类型[69], 后来的面向对象程序设计[70, 71]、ML等函数式程序设计语言[72], 等等.
(2) 结构化规约语言
早期的结构化模型规约语言有VDM-SL[27]、Z Notation[28, 73]等.VDM包括数据类型的规约和程序结构(即模块)的规约.数据类型的规约定义具有该类型的数据以及数据上的操作, 由一阶谓词逻辑描述数据的范围约束以及操作需要满足的约束.一个模块的规约说明程序变量及其类型以及一组过程或函数.过程和函数的功能约束由Floyd-Hoare逻辑来定义.VDM定义了模块的组合机制.Z-语言的Z-模式(Z-schema)可以描述数据类型和程序功能, 并统一使用一阶谓词逻辑描述集合、函数和关系, 故而其逻辑基础是一阶谓词逻辑和集合论.Z-语言的模块组合机制与VDM相似.VDM和Z都是以精化为核心的规约语言, 支持软件从需求规约到代码规约的自顶向下的瀑布开发过程模型.由于一阶逻辑包含在规约语言中, 所以可以描述模型规约需满足的性质.如果规约蕴含该性质, 则该归约满足此性质.因此, VDM和Z也支持包含分析验证的V型开发过程模型.
为了提供面向对象的软件规约和精化, VDM扩展到VDM++[74], Z扩展为Object-Z[75].在VDM和Z的基础和思想的影响下, 为了处理交互的分布式软件和基于服务的系统, 在类似基于数据状态的VDM和Z的静态规约语言中引进了事件和状态迁移行为, 发展了一系列的规约语言, 包括B[76]、Event-B[29]、Alloy[77]、JML[78]和rCOS[34]等, 这些规约语言都有明显的软件结构描述, 其中, JML和rCOS直接使用了现代高级程序语言的结构机制表示软件架构, 例如面向对象的继承和基于构件的软件界面和连接器(connector).
(3) 进程代数(演算)
为了设计开发并发和分布式系统, 出现了CCS[15]、CSP[13]、ACP[79]等进程代数(演算).CCS和CSP都最大限度地将并发通信系统的数据状态和数据计算功能抽象掉, 集中描述通信和同步以及二者之间的关系, 是基于事件的规约语言.CCS规约是一个CCS语法定义的表达式, 语义是通过结构操作语义来定义表达式描述的通信进程的行为演化.这样定义的CCS表达式的状态迁移规则构成了推导CCS表达式之间各种等价关系的形式系统, 这些等价关系可以表示成不同的互模拟(bisimulation)关系.CSP有比较丰富的程序语言因素, 例如外界选择、内部选择、同步并发等.CSP定义了一系列不同抽象层次的指称语义, 按表达能力递增的顺序有轨迹语义(trace semantics)、失效语义(failure semantics)和失效-发散语义(failure-divergence semantics).后来, CSP也有了完整的操作语义理论.基于进程代数的规约具有非常好的结构特征, 适合对复杂系统, 特别是并发、并行和分布式系统进行建模.
为了处理并发系统的其他特征, 如信息安全、移动、实时、混成、概率和随机, 这些并发模型均进行了各种扩充.例如, 为了处理实时系统, Reed和Roscoe扩充CSP到实时系统, 建立了Timed CSP[23]; 为了处理混成系统, 何积丰和周巢尘等人将CSP扩充到混成系统, 建立了混成CSP[80-82].再如:为了处理移动计算, Milner提出了π-演算[83], 后被Cardelli和Gordon进一步扩充为Ambient-calculus[84]; 为了处理信息安全, Abadi等人将π-演算改进成spi-演算[85]; 等等.Milner试图使用范畴论统一这些并发计算模型, 提出了Bigraph理论[86].
(4) 基于迁移系统的规约
迁移系统可以自然地表示系统的行为.典型的基于迁移系统的规约语言有Petri网[12]和Statecharts[87]等.基于迁移系统的规约语言往往有图形化表示, 称为可视化规约语言.Statecharts用Higragh进行形式定义, 图的节点代表系统执行的状态, 而一个节点到另一个节点的边表示从一个状态到另一个状态的迁移, 可将模型转化为规则形式定义, 构成一个推理系统.由于其执行模型是抽象机, 这样的图形语言可以构建可执行的规约(executable specification)或可执行的模型(executable model), 能够对系统行为进行仿真、测试.它们经常作为时序逻辑的解释(模型)使用, 可以用时序逻辑进行规约和证明其性质, 也可用算法判定其建立的模型是否满足一个时序逻辑公式.结果可以作为系统早期设计验证的依据, 以便尽早发现设计错误.但是这种形式规约组合性较差, 不容易对复杂系统建模.
为了对非功能性需求建模, 人们对标记迁移系统进行了各种扩充.以自动机为例, 其后续扩展包括:时间自动机[21]、混成自动机[88]、概率时间自动机[89]、随机混成自动机[90], 等等.而且这些模型不再局限于计算机领域, 已经广泛应用于控制、生物、物理、化学等诸多领域.
2.1.2 性质规约语言
性质规约语言基于程序逻辑系统, 通过逻辑公式来描述一组性质以定义所期望的系统行为.性质规约不直接定义系统的具体行为.基于性质的形式规约偏向于说明性的, 逻辑约束往往是最小必要的, 以给出较大的实现空间.Lamport指出, 系统需要满足的性质可以分成两类[91]:安全性质, 即不好的事情从不发生; 活性, 即好的事情一定能够发生.Alpern和Schneider证明, 任何性质均可以表示成这两种性质的交[92].
顺序程序设计早期的程序逻辑是Floyd-Hoare逻辑[10, 93].Floyd-Hoare逻辑的公式形如{Pre} P {Post}, 其中, Pre和Post是一阶逻辑公式, 分别称为前、后置断言; P是程序.通常, {Pre} P {Post}可以有如下两种解释.
a) 部分正确性:如果一个初始状态满足Pre, 且P由该初始状态的执行能够终止, 那么终止状态一定能够满足Post;
b) 完全正确性:如果一个初始状态满足Pre, 那么P由该初始状态的执行一定能够终止, 且终止状态一定能够满足Post.
Floyd-Hoare逻辑的推理系统是在一阶谓词系统基础上添加关于程序的公理和推理规则来建立的.类似的规约语言有Dijkstra的卫士命令语言的最弱前置条件演算[94].
然而, 这些早期的奠基性工作有很多不足之处, 如缺少对带指针和内存数据结构的程序规约机制、缺少并发程序的规约机制等等.后期有大量工作对Floyd-Hoare逻辑进行扩展, 形成了新的程序逻辑、规约和验证方法.分离逻辑[95]是对Floyd-Hoare逻辑的扩展, 以支持带有指针和内存数据结构的程序的验证.它由Reynolds、O’Hearn、Ishtiaq和Yang等人在2000年前后提出, 是近年来程序规约与验证领域的最重大突破之一.它在断言语言中引入方便描述内存形状和分离特性的分离合取和分离蕴含谓词, 并在规则中将Floyd-Hoare逻辑的不变式(invariance)规则替换为框架(frame)规则.分离逻辑最大的特色是对内存和数据结构的抽象描述, 它能够更方便、更模块化地支持类似C程序的指针程序的验证.
在Floyd-Hoare逻辑的基础上, 通过引入行为轨迹的变量或不变式, 建立了多个并发程序的规约语言, 有代表性的工作主要包括Owicki-Gries方法[96, 97]、Rely-Guarantee方法[98, 99]和并发分离逻辑[100].与分离逻辑类似, 并发分离逻辑对并发程序验证有很好的模块化支持.在其被提出之后, 有大量工作对并发分离逻辑进行扩充, 包括将Rely-Guarantee和并发分离逻辑结合, 以支持细粒度并发或者无锁并发程序的规约和验证.基于并发分离逻辑开展的工作可参见Brookes和O’Hearn的综述文章[101].除了这些针对串行一致性内存模型上的并发程序的程序逻辑外, 近年来还有一些工作对并发分离逻辑进行扩展, 以支持弱内存模型下的并发程序.比较有代表性的工作包括Vafeiadis及其团队提出的一系列在C11内存模型上的程序逻辑(如文献[102]), 以证明C11内存模型(子集)上的程序的正确性.
为了克服Floyd-Hoare逻辑中程序和断言的分离及无法表达活性, Pratt提出在模态逻辑中使用程序来定义模态算子, 建立动态逻辑[103].Kozen在动态逻辑中引入不动点, 建立模态μ-演算[104].在树结构上, 它的表达能力和二阶一元逻辑等价[105, 106].线性时序逻辑(LTL)[18, 107]和计算树逻辑(CTL)[108, 109]是并发系统规约和验证的常用语言.LTL和CTL的表达能力不可比较, 但都是模态μ-演算的真子集; Lamport提出了动作时序逻辑(TLA)[110]; Moszkowski等人提出了区间时序逻辑(ITL)[111].为了处理一些非功能性质, 这些逻辑均作了一些扩充.例如, 动态逻辑被扩充到混成系统, 称为微分动态逻辑[112]; LTL扩充到实时系统, 称为度量时序逻辑(MTL)[113]; LTL和CTL分别扩充到概率系统, 称为pLTL[114]和pCTL[115]; ITL扩充到实时系统, 称为时段演算(DC)[116, 117]等等.
2.2 形式语义学
形式语义学起源于对程序设计语言语义的研究.程序设计语言的语法是符号化的, 其语义就是该语言程序所描述的计算或者过程.在程序设计语言的早期, 语义用自然语言解释, 程序语言的解释器或编译器按照语义将该语言程序编译成计算机可处理的机器语言程序.这种自然语言解释的语义不精确、有歧义, 无法支持对程序正确性的严格证明和分析.为了帮助理解使用程序设计语言、支持语言标准化、指导语言设计、帮助开发更好的编译器以及分析证明程序的性质和程序之间的等价性, 需要对程序语言的语义进行抽象和严密的定义.为此, 出现了使用数学结构来定义程序语言语义的研究, 后扩展到各类形式规约语言, 形成了形式语义学.形式语义学(理论)研究形式规约语言语义的数学基础和构建方法, 提供研究形式语言表达能力、可靠性和完备性的数学手段.依据使用的数学结构和语义表示方法的不同, 形式语义研究方法可以分为4类, 即操作语义、指称语义、代数语义和公理语义.关于计算机语言的形式语义的综合论著可参阅文献[118, 119].
2.2.1 操作语义
操作语义(operational semantics)使用抽象解释器(有时也称为抽象机或者抽象函数)定义语言语义, 着重模拟数据加工过程中计算机系统的操作.定义操作语义需要一个抽象机模型.最早有形式语义的语言是McCarthy用Lambda-演算定义的LISP, Lambda-演算的表达式求值过程是用抽象机定义的.1981年, Plotkin提出了结构化操作语义[120]作为定义程序设计语言的方法.目前最为常见的是标号迁移系统(labeled transition system), 基本想法是把程序执行描述成标号迁移系统, 其中的状态为程序执行期间任意时刻观察到的变量取值, 迁移关系规定如何从一个状态迁移到下一个状态, 一般定义为一组迁移规则, 每条迁移规则对应一个语句, 称为标号.一条语句的语义是由一组以其为标号的规则定义; 标号规则具有组合性, 即, 一个复合语句的规则可以由其成分语句的规则组合而成.
操作语义是最早使用的形式语义方法, 用来给出顺序程序的语义, 此时, 状态均是一些简单的数据结构, 迁移关系一般都是确定的、离散的, 也不需要考虑标号间的通信和同步.为了定义复杂程序的操作语义, 例如面向对象程序、并发程序、实时程序、概率程序、混成系统等, 人们对迁移系统进行了各种扩充, 或扩充它的状态, 或扩充它的迁移关系, 亦或两者同时扩充.例如, 为了定义面向对象程序, 人们扩充了程序状态, 引入堆和栈等复杂数据结构[121]; 为了处理并发程序, 人们扩充了标号迁移关系, 允许使用标号描述通信和同步[83]; 为了描述概率和随机程序, 允许以给定的概率或者随机选取迁移规则[122]等等.
操作语义基于抽象机, 与计算机最为接近, 可描述实现方面的执行细节, 操作性比较强, 适合于开发语言编译器以及编译优化的应用.在语义中, 状态是被直接表示和操作的, 也比较适用于形式验证中基于状态搜索的模型检验方法里的语义模型.然而, 在大规模或无穷状态的系统中, 抽象机上的推理系统比较弱, 不易进行基于演绎推理的形式验证.
2.2.2 指称语义
指称语义(denotational semantics)将语言的基本语法成分解释成为数学对象(称为指称), 用数学对象上的运算来定义语言的语义.论域理论是指称语义的数学基础, 讨论各种语言成分的指称的数学结构, 并提供数学工具, 从而在各种数学结构之上定义语言语义和推导语言成分特性.例如, 将程序语言的基本语法实体的指称定义为程序状态空间上的函数和泛函, 复合语法实体的指称由构成它的子成分的指称复合得到.
建立指称语义的首要任务是确定一个相应的论域理论, 即确定程序语言的解释域[123].处理不同的计算现象需要不同的语义, 例如, 可以定义不关心是否停机的顺序程序的语义, 也可以定义需要刻画停机的语义.显然, 不同的语义需要不同的论域.以CSP为例, Hoare等人提出了CSP的迹语义模型、失效-发散-迹语义模型等[14, 124], 这些语义的区别在于失效-发散的语义可以刻画程序死锁以及活锁, 从而分析系统的活性.论域理论的研究随着程序对象的不同而不断地发展着, 例如, 针对Timed CSP, 人们扩充了迹语义模型和失效-发散-迹语义模型, 分别提出了带时间戳的迹语义模型和带时间戳的失效-发散-迹语义模型[23, 125].
指称语义的论域理论具有较多可利用的数学性质, 有利于探讨不同语义论域及不同语义间的关系, 特别是与公理语义和操作语义间的关系.论域表示理论讨论了不同语义论域间的关系, 提供了不同语言形式语义间的关系[126]; Hoare和何积丰基于一阶关系演算提出了程序统一理论(unifying theories of programming, 简称UTP)[39], 其基本想法是, 通过伽罗瓦连接(Galois connection)给出同一语言不同语义间的转换关系.指称语义可以较好地支持形式规约的精化.
2.2.3 代数语义
代数语义(algebraic semantics)用代数结构来定义计算机语言(特别是代数规约语言)的语义, 是在抽象数据类型的基础上发展起来的[118].在抽象数据类型中, 基调是用代数结构描述数据类型的语法(类子和类子间的运算), 运算的推导规则用一组公理(等式或者条件等式)描述, 这样, 满足这组公理的模型就是这个抽象数据类型的一个代数语义(称为∑-代数, 其中, ∑是基调).基于代数语义, 可以利用模型论和范畴论方法来推理该语言的程序性质.
抽象数据类型将数据对象及对象上的操作封装、数据类型的特性与实现分离, 具有模块化和可复用的性质.它与软件开发过程匹配比较自然, 首先设计较小的抽象数据类型, 然后逐步扩充形成较大的抽象数据类型体系; 这个过程中, 抽象数据类型间可讨论层次一致和充分完备等性质.一个抽象数据类型可能有多个语义模型, 其中, 初始代数(initial algebra)和终结代数(terminal algebra)在∑-同构意义下都分别唯一, 采用初始(终结)代数模型作为语义的方法称为初始(终结)语义方法.抽象数据类型基始完备的描述可以唯一地扩充为相对完备, 原描述的终结模型恰好就是其极大扩充的初始模型, 表明了初始代数语义与终结代数语义之间的内在联系[127].把一个规约或程序视为抽象数据类型时, 就有了它的代数语义.对于规约或程序, 可能对某些输入是无定义的, 故定义了偏抽象数据类型和偏∑-代数.另外, 在处理程序开发中, 两个不同的程序会有相同的执行效果, 相应的代数语义要处理好等价的问题.
代数语义与代数规约的关系密切, 主要用于解决基于代数规约的形式化开发中程序正确性的推理, 抽象程度比较高.如果将等式看作是从左至右的重写规则, 代数规约就以项重写的形式可执行, 成为了一种可执行规约.
2.2.4 公理语义
公理语义(axiomatic semantics)直接使用形式逻辑来描述程序的语义, 其基本思路是, 在已有的形式逻辑系统的基础上增加所有程序必须满足的基本命题(程序公理).每个程序的基本语句都有一组公理和推理规则, 它们与断言逻辑一起构成程序逻辑的证明系统.程序性质的规约和验证就可直接在该形式系统中进行.程序逻辑的表达能力、可靠性、完备性以及可判定性都可归结为数理逻辑上的元性质, 程序逻辑的解释模型通常就是程序语言的指称语义或操作语义.
最为常见的有基于一阶逻辑扩展的Floyd-Hoare逻辑、谓词转换器(predicate tranformer)等.Floyd-Hoare逻辑最初是针对顺序程序提出来的, 并扩展至并发程序、实时系统、混成系统甚至量子系统等.面向指针程序和面向对象程序产生了分离逻辑及其变种, 这些研究把Floyd-Hoare逻辑的应用真正地推进到实际的程序验证.人们还提出了动态逻辑、模态逻辑、时序逻辑等用来作为定义程序公理语义的形式系统.公理语义在形式验证中的应用是比较多的.
表 2给出了这4种语义之间的一个比较.程序语言的形式语义的机器定义是建立形式验证的基础.例如, 可以使用定理证明器的元语言来机器实现程序语言的语义, 也可直接用函数式语言来实现目标程序语言的语义. K框架基于重写的可执行语义框架, 用来定义程序语言的操作语义, 能够解释执行程序、空间搜索和模型检验, 支持该语言程序的验证[128].基于K框架, 定义了C99和Java 1.4的形式语义[128, 129].
 |
Table 2 Comparsion of formal semantics表 2 形式语义风格之间的比较 |
2.3 形式化开发与软件构造
形式规约和开发方法遵循软件开发方法的基本原理, 包括关注点分离和逐步精化.在形式规约和验证的基础上, 软件形式化构造活动包括针对形式规约多视角建模、不同抽象层上规约间的精化以及程序综合等.
2.3.1 基于规约的形式化开发
形式规约必须具有良好的性质.形式系统的一致性表明其是否语义可满足, 换言之, 形式规约的一致性刻画了其是否是可实现的.即:它对应满足关系的语义域非空, 说明这个规约有满足其约束的实现, 理论上是可实现的.当形式规约用来描述需求时, 则成为判断需求规约可行性的重要途径.另一方面, 一般不要求形式规约是完备的, 不完备的规约可以给实现者更多实现方法上的空间, 也给了开发人员平衡未来实现在功能和性能上的空间.一个规约本身就可以有多个不同的实现, 例如实现的数据结构和算法.
与软件的其他建模方法一样, 形式规约可以从不同的角度用不同/相同的规约语言来描述系统, 即所谓的多维视角规约方式, 如图 2所示.例如, 一个系统(需求)规约可包括数据模型规约、数据功能规约、交互通信协议规约以及动态的状态迁移行为模型.复杂的系统还会有更多的视角, 尤其是非功能方面的.数据模型可以用代数规约或Z-语言[73]描述, 数据功能规约可以用Floyd-Hoare逻辑[93], 交互通信协议可以用CCS[15]、CSP[14]等, 而动态行为可以用自动机[130]或Statecharts[87].功能规约描述系统功能和子功能之间的关系, 例如数据功能规约和交互模型.行为规约描述系统的时序、容错、时空等约束.系统规约往往是相互关联的, 各个视角规约内部和规约之间都有一致性约束, 以保证规约是可实现的, 而系统同时满足这些约束就能得到系统完整的正确性.多视角的形式规约有模型的, 也有性质的, 或者两者混合的.使用不同语言需要各种语言语法和语义的一致统一, 对此, rCOS在UTP基础上有初步的研究结果[131].也可以用单一的形式规约语言, 如Event-B[29].但是每种语言一般都有局限性, 理论和工具支持也不够充分, 所以有必要进一步推进各种形式化方法在Institutions[39]或者UTP[40]等的基础上的统一及工具的集成.
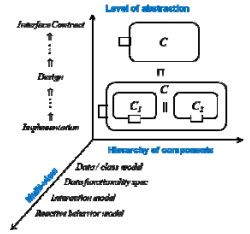 |
Fig. 2 Formal development methods—Multiple views图 2 形式化开发方法——多维视图 |
环境建模是软件开发中不可忽略的内容, 形式规约同样需要包括对环境模型或性质约束的规约.在包含了环境的形式规约中, 要区分环境与系统建模的不同, 环境规约是一组假设[64].例如在模型规约中, 环境状态和变迁在可观、可控上的不同.对于大型复杂系统的规约, 我们需要尽可能显式地表达出对环境的假设, 同时选择合适的部分规约的抽象层次和形式, 以灵活应对环境的动态和多变.含环境的规约一般可以定义为系统或构件的接口合约(interface contract).合约的抽象形式是一组关于系统和环境的谓词(A, G), 其中, A描述系统环境应该满足的条件, G是在环境满足A的前提下系统行为所满足的要求.
软件开发过程中, 形式规约方法与设计方法一样是逐步开发的.以形式规约为制品的设计形成了形式化开发的主线.形式化开发中最重要的设计活动是精化, 它是将形式规约的抽象层次向实现加以变换.例如, 一个层次的模块分解为下一个层次的若干模块, 或者具体化一个抽象数据类型的表示类型.精化需要保持正确性, 并具有组合性, 不同抽象层次逐步开发的形式规约形成了规约的精化链.基于合约的规约有很好的可组合性并支持建立精化演算.图 2所示的需求分析结果可以是系统或构件与环境的合约规约, 而架构设计中子系统或构件C1和C2在各自的合约基础上加以组合, 计算出组合系统的合约规约, 并保证是上层合约的精化, 即保证满足上层规约的所有需求性质.整个设计过程可以理解为一个逐步分解和精化的过程.
精化演算是以组合化方式支持逐步求精的形式推理系统, 最早是面向顺序程序[132, 133], 近年来发展到了反应式系统精化[134, 135]和构件化软件的精化[34].在形式化逐步求精过程中, 精化都可以是形式化的, 每步精化需要证明下一层的规约满足上一层的规约, .在实际应用中, 因为成本问题, 工业界往往不这么做.但是, 有精化演算指导的设计过程无疑能提高设计质量.软件工程中建立的一系列设计模式(design pattern)在一定意义上就是对精化技术的一种非形式化的工程实践.如果在安全攸关的应用开发时能够尽可能地形式化, 则对于确保安全性是有显著意义的.在形式化开发中, 精化过程的一种重要技术是程序综合, 即, 从规约能够直接生成程序, 参见第2.3.2节.
在逐步求精的过程中, 形式化方法有效支持关注点分离的软件工程原则.一般情况下, 数据功能、交互通信协议和动态规约可以分别求精; 从无时间的规约到有时间的规约一般可以是精化(时间模型的健康条件)[40], 容错也可以视为原来设计规约的精化[136].另外, 基于形式化的设计精化一般有很好的可组合性, 分解和精化支持模型重用、证明分析过程重用、代码重用, 所以有效支持分而治之的工程原则, 尤其是基于构件和服务化系统的开发.
研究、理解和处理软件开发的复杂性, 一直是驱动软件工程发展的核心问题.针对Brooks指出的软件开发复杂性来源[137], 形式化开发从需求规约到软件代码, 将软件开发建立在一个有理论基础和规则的工程过程中, 这正是1968年NATO软件工程会议所提出的目标.我们可以使用形式化方法讨论和说明一种软件开发方法的科学性以及开发过程的可信性.在这个过程中, 形式化可以提高开发的严密性, 用抽象和分解手段有效处理复杂性, 尤其是通过精确描述复杂系统行为、基于精化的设计、将开发过程制品转换成可以分析验证的规约等手段, 能够有效地提高在巨大的设计空间中逼近最合适设计的能力.
2.3.2 程序综合
程序综合(program synthesis)是指使用指定的编程语言自动生成符合程序规约的技术.程序综合问题由Church[138]于1960年代初提出, 一直是计算机科学的核心问题和挑战, 被认为是计算机科学的圣杯[139].最初关于程序综合的方法是基于转换的程序综合(transformation-based synthesis)[140], 它将一个高层的程序规约通过反复转换为较低层的程序规约, 最终生成期望得到的程序代码.规约间或规约与程序间的转换要么归结为树自动机接受语言是否为空的问题[130], 要么归结为两个玩家博弈取胜的策略问题[141].但这种方法能够自动生成的代码非常有限, 很长一段时间没有发展.近些年, 随着Pnueli提出由时序逻辑公式自动综合反应式系统控制程序的成功, 有复苏迹象[139].
现在较为流行的程序综合的方法主要基于演绎推理的方法及其变种, 特别是与人工智能相结合的方法.在构造数学中, 1930年代即有了通过把子问题的解组合到一起的方式来构建证明的思想[142].在第一个自动定理证明器开发出来之后, 人们提出了许多基于演绎推理的演绎综合(deductive synthesis)方法[143-145], 主要思想是:首先, 使用定理证明器构造用户提供的程序规约的一个证明; 然后, 基于Curry-Howard同构关系[146], 使用该证明来生成相应的程序代码.
基于演绎的综合方法假定用户可以提供需求的一个完整的形式规约.但在很多情况下, 提供一个完整的形式规约并不比写出一段程序更加容易.为此, 人们提出归纳式程序综合(inductive program synthesis).归纳式程序综合基于归纳式规约, 例如输入输出对、示例(demonstration)等.Shaw等人[147]发展了从单个输入输出样例中学习语法受限的LISP程序的框架.Summers[148]和Biermann[149]发展了一种从多个输入输出对中学习语法更加丰富的LISP程序的方法.Smith[150]发展了以一系列程序执行记录为示例来推断递归程序的方法.除此之外, 有很多开创性的工作通过基因编程的技术来自动进化出符合规约的程序[151].这些方法从达尔文的进化论中得到启发, 通过持续不断地将一个随机种群进化到新的世代, 最终生成所需的代码.
还有一些方法允许用户在程序规约以外提供代码框架(或是语法).这样做有如下两个优点:首先, 提供的语法极大地缩小了代码空间, 从而极大地提升了搜索效率; 其次, 由于程序是按照给定的语法生成的, 学习到的程序更容易读懂.SKETCH[152]系统允许用户提交代码片段, 然后再根据用户提交的规约补全代码片段.FlashFill[153, 154]使用正则表达式定义了一个操作字符串的领域专用语言, 然后基于解释空间(version-space)的代数来高效地从输入输出对中获取对应的程序, 在微软表格中得到了广泛的应用.
很多现代程序综合方法建立在多种生成框架之上.这些框架不仅允许用户定义程序空间, 也允许用户定义生成程序的一些性质.然后, 程序综合框架将这些定义包装成一个在给定问题域内的高效的程序生成工具, 例如SKETCH[152]、PROSE框架[155]和ROSETTE虚拟机[156].
3 形式验证
形式化方法最显著的作用是能够对形式规约进行验证.形式验证常见的有两种形式:一种是推理“系统模型规约是否满足其性质规约”, 这时, 模型规约偏向操作型, 性质往往是说明型的; 另一种是推理“系统的一个模型规约是否与另一模型规约有精化或等价关系”.这些推理过程给出了一套静态方法来预测系统的行为:用户可以描述系统行为的所期望性质或者开发过程中不同抽象之间关系的猜想, 形式验证通过机械化的方式来证实或者证伪这个性质或者猜想, 从而提高用户对规约和系统的可信程度.形式验证方法主要包括演绎式的定理证明和算法式的模型检验.
3.1 定理证明
基于定理证明的形式验证将“系统满足其规约”这一论断作为逻辑命题, 通过一组推理规则, 以演绎推理的方式对该命题开展证明.基于定理证明的验证大部分是以程序逻辑为理论基础的, 但是程序逻辑并非唯一的验证方法, 例如, 我们可以基于程序的操作语义直接表达程序执行的安全性、正确性等各种性质并证明相关定理[58, 157].
Floyd-Hoare逻辑[10, 93]是一种经典的基于定理证明的验证系统, 其验证对象是顺序程序.Floyd-Hoare逻辑通过一组和程序语言语句对应的公理和规则, 将对程序的验证转化为一组数学命题的证明, 这组数学命题往往称为验证条件(verification condition, 简称VC).Owicki和Gries提出一种通用的并发程序验证方法[96], 该方法将每个并发任务当作顺序程序单独进行验证, 然后检查任务之间的无干扰性(non-interference), 以确保单个并发任务的验证过程不会因为其他并发任务的执行而变得无效.这种方法的问题是缺少可组合性, 这是由于在进行无干扰性检查时, 需要检查所有并发任务的代码, 因此并不能在真正意义上实现对单个并发任务进行独立验证. Jones在此方法的基础上进行扩充, 提出了Rely-Guarantee方法[98], 解决了可组合性问题.Rely-Guarnatee方法将并发任务间的接口抽象为Rely和Guarantee两种不变式——Guarantee是对任务自身行为的抽象, 而Rely则是对任务所能接受的环境行为的抽象.在检查任务之间的无干扰性时, 不需要逐行检查任务的代码, 只要检查不同任务之间的Rely和Guarantee接口的匹配即可, 要求每个任务的Rely被其他每一个任务的Guarantee蕴含(即Rely得到满足).由于不再需要逐行检查所有任务的代码, Rely-Guarnatee方法允许对单个任务进行独立验证, 因此是一种具备可组合性的方法.
除了通用的Owicki-Gries方法[96]外, Owicki和Gries还针对良好同步(properly synchronized)的并发程序提出了一种简化的程序逻辑[97].逻辑要求并发任务对共享数据的访问必须在互斥锁所保护的临界区内进行.共享数据必须满足一定的不变式, 该不变式构成了并发任务之间共享数据的协议.每个任务进入和退出临界区时, 必须保证共享数据满足不变式.这是一种具有可组合性的验证方法:每个并发任务可以单独进行验证, 只要任务对共享数据的访问满足不变式, 任务之间自然具备无干扰性.然而, 如同Floyd-Hoare逻辑不支持指针和内存数据结构一样, 该方法也不支持带指针和内存数据结构的并发程序.并发分离逻辑[100]是结合分离逻辑思想对这种Owicki-Gries方法的扩充, 实现对带指针和内存数据结构的并发程序的模块化验证.它充分利用了分离逻辑中的分离合取能够方便地描述内存空间分离这一特点, 将内存从逻辑上分为共享内存以及每个任务自己的私有内存, 并要求不同内存之间是分离的.这时, 针对共享数据的不变式便只需要描述共享数据自身, 而无需描述内存的其他部分.
关系型程序逻辑是对Floyd-Hoare逻辑从一个新的角度进行的扩展, 它可以验证两个程序之间的关系, 或者一个程序在两种输入下的行为之间的关系.前者可用于程序精化的验证, 而后者则可用于信息安全性质, 例如信息流控制(information flow control)机制的验证.Benton[158]和Yang[159]较早提出关系型程序逻辑.Beringer和Hofmann提出将关系型程序逻辑应用于信息流控制[160].Bathe在关系型程序逻辑方面开展了较多研究, 主要将其应用于信息安全性质验证[161].Turon等人[162]和Liang等人[163]提出了关系型程序逻辑开展并发程序的精化验证.作为对关系型程序逻辑的扩展, Sousa和Dillig提出了笛卡尔霍尔逻辑, 用于验证k-safety, 即, 程序k次不同执行之间的关系[164].
按照证明方式和自动化程度的不同, 基于定理证明的验证又可以分为两类, 即基于自动定理证明器的自动验证和基于人机交互的半自动验证.
3.1.1 基于自动定理证明器的自动验证
近年来, 随着自动证明理论的发展和计算机处理器能力的大幅增强, 自动定理证明器的能力得到大幅提升, 基于自动定理证明的验证也得到很大发展.目前常见的程序证明器(program verifier)包括Dafny[165]、Why3[166]、VeriFast[167]、Smallfoot[168]等.这些程序证明器大多基于某种具体的程序逻辑.给定程序及其规约, 证明器能够自动决定针对程序的每条语句使用程序逻辑中的何种公理或规则, 并产生相应的验证条件作为证明义务.最终, 产生的验证条件被送到自动定理证明器中, 由定理证明器完成对验证条件的证明.目前使用最广泛的定理证明器是微软开发的Z3[42], 其他常见的证明器还包括CVC4[43]、Yices 2[169]等.
使用各种定理证明器和自动化程序验证技术, 人们已经实现了对一些相对实用的、较大规模的具体系统的验证.具体工作包括微软研究院Hawblitzel等人对操作系统内核、分布式系统等系统的验证[170, 171].Hawblitzel等人将源程序翻译到中间语言Boogie[172], 在Boogie上开展验证, 并将生成的验证条件交给Z3自动证明.近年来, 类似的工作还包括华盛顿大学对操作系统内核[173]和文件系统[174]的自动验证工作.
基于自动定理证明的验证工作的优点在于验证的效率较高, 不需要人手工写证明.然而, 由于自动定理证明中很多问题是不可判定问题, 而且各个定理证明器又有各自的能力限制, 因此能够表达和证明的性质有限.为了能够实现自动证明, 很多时候需要对待证明的性质和待验证的代码本身都进行重写, 甚至为了迁就验证的自动化而牺牲待验证的性质以及代码的功能.例如, 在对操作系统内核的自动化验证工作[173]中, 为了实现“一键完成(push button verification)”这一特性, 内核中带有循环语句的代码都被移到了内核外部, 从而这部分代码不再属于自动化验证的目标.
3.1.2 人机交互的半自动化证明
基于定理证明的另一类验证工作, 则不强调使用计算机实现验证的自动化, 而是利用计算机来解决证明在计算机中的表示问题以及自动检查证明的正确性的问题, 证明的构造则由人手工和机器交互, 以半自动化的方式完成.很多辅助定理证明工具, 如Coq[40]和Isabelle/HOL[45]等, 都是针对这一目的进行开发的.这类工具往往是利用类型系统和逻辑之间的Curry-Howard同构关系[146], 将构造证明的过程转化为编写程序的过程, 而证明的正确性检查也变成了类型检查问题.
这类人机交互的半自动化验证工作往往需要大量的手工劳动来构造证明, 虽然在辅助定理证明工具中提供了一些基本的证明策略(tactics)和引理库来减少证明负担, 但在实际代码的验证中, 往往平均一行程序需要手工书写20~30行证明脚本.然而, 这种方法的优点在于无需牺牲规约和代码的表达能力, 特别是程序规约可以用表达能力很强的逻辑(如在Coq和Isabelle/HOL中使用的高阶逻辑)来表示.而且证明自身在机器中有显式表示, 其正确性可以被自动检查, 因而我们无需依赖自动定理证明算法的正确性, 验证的结论也就更加可信.
3.2 模型检验
定理证明中, 形式验证把待证明的性质直接作为了一个数学定理来证明, 也称为演绎式验证.与演绎式相对应的一种方式是模型检验[175-177].模型检验分别由Clarke和Emerson、Queille和Sifakis在1980年代初各自独立提出[19, 176], 其基本思想是:检验一个结构是否满足一个公式要比证明公式在所有结构下均被满足容易得多, 进而面向并发系统创立了在有穷状态模型上检验公式可满足性的验证新形式[178].
模型检验通过自动遍历系统模型的有穷状态空间来检验系统的语义模型与其性质规约之间的满足关系, 其基本框架如图 3所示.模型检验中最常见的是时序模型检验或逻辑模型检验, 其系统规约大多是基于模型的规约, 使用操作语义描述系统行为, 形式模型使用自动机、标记迁移系统等; 待检验的性质是用时序逻辑描述的基于性质的规约.如果系统模型不满足性质, 模型检验算法会给出系统行为不满足性质规约的反例, 用户可以根据反例进行分析和调试; 如果模型检验未发现反例, 则系统一定满足所检验的性质.
 |
Fig. 3 Framework of model checking图 3 模型检验框架 |
3.2.1 基本途径
模型检验的核心是有穷状态空间上的遍历策略和算法, 主要有显式方法和隐式方法.显式方法是通过状态计算来遍历状态空间, 隐式方法是通过不动点计算来遍历状态空间.两者的本质都是有穷状态空间的穷尽搜索.因而, 模型检验的关键问题就是如何应对系统状态爆炸, 在可表示的状态空间和有效的时间内完成搜索.对于这个问题, 主要有3类途径[179].
(1) 结构化方法:利用定义系统的语法表达(模型)结构来缓解状态空间爆炸问题, 典型的方法有对称模型检验[180-182]、On-the-fly的状态空间搜索[183, 184]、偏序模型检验[185-187]、参数化模型检验[188, 189]等等;
(2) 符号化方法:将模型的迁移结构的状态和迁移编码为逻辑公式, 这种符号化编码能够有效压缩表示状态集合的数据结构, 状态变迁的操作也相应高效.符号化的编码方法常常基于BDD[190]、命题公式[191]或者无量词的一阶约束[192]等等;
(3) 抽象方法:将复杂系统的状态空间结构归约为较小的同态映像, 后者是前者的一个上近似(over- approximation), 从而把原系统的验证转化成模型检验可以处理的问题[193], 例如谓词抽象方法等.而作为一种更一般化的方法, 抽象解释是一种基于序集合上单调函数对程序形式语义进行可靠近似的理论, 为程序自动分析提供了一个通用的框架[194, 195].
模型检验的其他途径还包括基于自动机理论的模型检验, Vardi和Wolper提出可以基于ω-自动机来进行自动验证[184].时序逻辑模型检验问题可以归结为基于自动机理论的模型检验.在这个途径中, 时序逻辑性质自动转换为一个自动机, 这样, 系统和性质都建模为自动机, 模型检验问题就归结为自动机的语言包含、判空等问题.SPIN模型检验工具就是基于这种方法.
模型检验在建立了系统模型和性质描述后, 验证过程是自动的, 并且在证伪时能够给出调试用的反例.它对于并发系统的验证比较有优势, 而且可以在不同抽象层次的模型上应用, 性质规约也往往是部分规约, 可以在系统设计全周期使用.但是它要求模型是有穷状态空间的, 或者能够在验证中转换到有穷的状态空间抽象上, 这在一定程度上限制了模型检验的应用.无穷状态系统的模型检验在相当一部分重要的应用场景是可行的, 其基本思路是利用符号化方法或数据抽象的方法将无穷状态系统转换为一个“性质等价”的有穷状态表示系统的抽象[196-198].例如实时时序逻辑性质的模型检验问题, 由于时钟变量是稠密的, 实时系统模型(时间自动机)的状态空间是无穷的, 模型检验时用Region来抽象系统状态的集合, 建立基于Region的状态变迁系统, 用来遍历状态空间以检验性质[199].典型的实时模型检验工具有UPPAAL[200].但是, 实时模型检验的可扩展性仍然是所面临的巨大挑战.
实际系统中存在不确定性, 这在信息物理融合系统是固有的, 例如系统中物理部件的信息感知不稳定、传输丢失等等.在这些系统模型的描述中, 通过引入概率或者随机元素来表达系统的不确定性, 并在设计策略中, 通过容错、容变机制来获得期望的量化性质.这类系统量化性质的模型检验有两种途径.
● 概率模型检验[201], 其在系统(例如标记变迁系统)中引入概率迁移, 采用可描述随机行为数学结构(例如马尔可夫链)为形式语义, 通过数值计算的方式检验此类系统是否满足所期望的概率时序逻辑性质(例如, 系统在给定时间内完成相应功能的概率).典型的概率模型检验工具有PRISM[202];
● 统计模型检验[203, 204], 其模拟有穷多次的系统执行, 然后通过假设检验来推断这些样本是否提供了统计证据以表明系统满足或违反性质.
概率模型检验的复杂度高; 统计模型检验避免了穷尽搜索, 但其结果具有一定的置信区间.
3.2.2 软件模型检验
软件系统属于无穷状态系统, 即使状态有穷, 其状态空间规模也往往远超当前计算机可处理的范围.在硬件系统模型检验取得巨大成功的时候, 软件模型检验所面临的挑战依然严峻.对于无穷状态系统, 符号化可达性分析都可能不终止.软件模型检验的核心问题是如何建立规模可检验的软件模型(抽象).给定软件S及待验证的性质p, 抽象模型检验就是建立一个抽象映射α, 并建立S⊨p(即S满足性质p)和α(S)⊨ p的关系.若S⊆α(S), 则称α(S)为S的上近似(over-approximation); 如果α(S)⊆S, 则称α(S)为S的下近似(under-approximation).
我们可以知道:当抽象不满足性质, 得到的反例一定是真的反例.但是, 抽象满足性质不能得到软件行为满足性质, 故下近似往往用于调试.如果采用上近似, 我们可以知道, 当抽象满足性质就可以得到软件行为一定满足性质, 但是当抽象即使证伪, 得到的反例不一定是真的违反了性质的软件行为, 可能是伪反例.如果不能成功地检验得到抽象满足性质且不能成功找到可行反例, 则说明建模可能过于抽象了.软件模型检验要获得足够精确的上近似, 需要通过抽象精化的方法得到更为精确的模型, 而且这个过程能够通过伪反例的信息来指导获得, 这就是软件模型检验的反例制导的抽象精化方法(CEGAR)[205, 206], 如图 4所示.
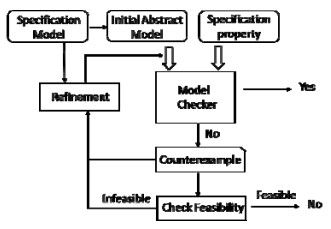 |
Fig. 4 Framework of counter-example guided abstraction refinement图 4 反例制导的抽象精化框架 |
当模型检验抽象得到反例时, 首先检验反例路径是否是可行的, 这通常通过基于反例路径的编码约束求解得到.如果不是可行的, 即反例的路径公式是不可满足的, 基于语法的精化就可以通过加减合适的谓词进行抽象精化.该方法的精化局限于程序中显式可刻画的关系.另外一种精化方法是基于插值的方法, 通过Craig插值发现可验证待验证安全性质的隐含关系的谓词.基于插值的方法能够获得比基于语法的精化更高的效率.基于抽象精化的模型检验工具有SLAM[207]、Blast[208]、CPA checker[209]等等.对于无穷状态的软件模型, 还可以通过编码为Horn短句形式求解来进行模型检验[210, 211].
与一般意义上的模型检验不同, 限界模型检验[191, 212, 213]通过对模型参数限界, 即将模型空间爆炸涉及的参数(例如循环次数、并发数等)限制在一定范围内, 验证系统模型在此深度内是否满足系统规约.具体做法是:将系统在有限步长内的行为编码成一组约束, 然后使用约束求解器(例如SAT、SMT求解器)检验是否存在相应可行的行为.需要注意的是, 限界模型检验已经把模型语义改变了, 因此即便限界模型检验没有发现错误, 也并不严格保证原系统在参数限定范围之外的行为也一定满足所检验的性质.随着约束求解技术的提高, 限界模型检验方法得到较大范围的应用.这主要有两方面的原因:一方面, 限界模型检验着眼于发现系统中的问题, 证伪时保持了模型检验能够反例发现的特点; 另一方面, 经验表明, 系统的缺陷往往在较小的深度就可以检测出来.同时, 限界模型检验方法中也可以综合应用基于数据约减和控制约减的方法, 提高了可扩展性.限界模型检验在软件自动验证中是常见的途径, 尤其是在并发程序的模型检验中.在目前的SV-COMP并发组比赛中, 限界模型检验方法具有绝对的优势[214].它的优点在于避免了开销大的不动点计算、较高的错误发现效率、不需要处理不变式, 并且可以根据计算资源能力调整验证的限界值.然而其不足也很明显, 方法上它不是可靠的.从提高系统可信的角度上看, 限界模型检验是一种简单、有效的复杂软件自动检验方法.
在软件模型检验中, 利用静态分析、符号执行等方法抽取程序模型, 以及基于路径的模型检验等静态和动态结合的方法, 也是有效提高模型检验扩展性的重要途径[3].近年来, 将模型检验与定理证明有效地结合也是一个有前景的方向.
4 形式化方法的应用
形式化方法在工业界硬件系统设计应用上十分成功.1992年, Clarke团队利用SMV验证了IEEE Futurebus+标准896.1-1991中Cache一致性协议.协议用SMV输入语言(规约语言)建模, 然后使用SMV验证规约行为(迁移系统)是否满足Cache一致性的性质规约, 结果发现了一些过去未发现的潜在错误[215].SRI和Rockwell Int’l合作使用PVS系统, 规约和验证了209条AAMP5指令中的108条, 验证了11条代表指令的微码, 发现了微处理器设计中若干微码的错误[216].1994年出现的Intel Pentium浮点单元中的缺陷产生了巨大的影响, 促使了形式化方法在硬件工业界的使用.Intel的Kaivola团队在Intel Core i7验证项目中, 利用形式化方法, 花费了约20人年验证了Core execution cluster, 在Intel建立了算术功能验证的金标准, 并为其他CPU和GPU的项目所采纳[217].该项研究获得了2013年的Microsoft Research Verified Software Milestone Award.20世纪90年代后, 形式化方法, 特别是模型检验在硬件设计验证上的成功, 效果得到了工业界的认可.其主要原因是:系统边界相对清晰、模式较为明显、动态性不强以及本质上状态空间有穷.随着计算能力的提高, 形式化方法能得到较好的费效比.
软件形式化方法的应用比硬件要早, 但在工业界的影响要小很多, 其主要原因是软件系统的复杂性远高于硬件, 相应的软件系统形式化工具水平也远低于硬件形式化工具, 特别是在形式验证工具方面.即使如此, 形式化方法也得到了一些具有显示度的应用.一个早期的成功案例是, 在IBM CICS(客户信息控制系统)项目中, 采用Z方法来描述这个大型交易处理系统的部分系统的规约, 结果显示, 与传统的开发方法相比, 开发成本降低了9%, 而在开发后期发现的错误数量减少了一半左右[218].这是一个对遗留系统进行形式规约重新开发的例子.在软件开发中, 使用形式规约保证系统质量的例子还包括丹麦数据中心DDC在1980年代利用形式化方法开发的ADA语言编译系统, 该系统成为了一个长期服役的商用产品[219].B方法使用在了Paris地铁的14号线系统和Paris Roissy机场无人驾驶线系统的关键部分中, 大约占整个软件系统的三分之一[220].Tokeneer ID Station是Altran Praxis为美国NSA开展的项目, 该项目希望通过实证研究来验证通过CC高等级安全测评、ISO/IEC 15408计算机安全认证是否经济可行.它可以看作是一个关于生产率和质量的对照实验.在这个小规模的安全系统中, 形式规约使用的是Z语言, 设计和形式规约精化使用的是INFORMED过程, 实现语言是SPARK Ada, 验证工具是SPARK工具集, 并使用自顶向下的系统测试[221].Tokeneer项目是工业界有效应用软件形式化开发的成功案例, 该项目获得了2011年Microsoft Research Verified Software Milestone Award.
形式化方法应用在工业界的影响不断增大, 自2001年, 形式化方法工具获得了4次ACM软件系统奖, 包括SPIN(2001)、The Boyer-Moore Theorem Prover(2005)、Statemate(2007)、Coq(2013).形式化方法的实践和相关经验可参见综述性文献[220].
由于形式化方法本身是有开销的, 故在应用中合理考量其应用的经济性是必须的.形式化方法在安全攸关的系统(航空、航天、核、铁路等领域)中往往得到较多的应用, 一些软件安全性保证标准, 例如DO-178B、DO- 178C、DO-333、Common Criteria、SIL1-4都在最(较)高层对系统开发中使用形式化方法提出了要求.美国JPL飞行软件团队使用SPIN模型检验器及其C代码模型抽取扩展, 分析了火星科学实验室任务(MSL)中多线程代码的竞争条件, 这些代码有120个并行任务在实时操作系统控制下运行[222].在国家自然科学基金委员会“可信软件基础研究”重大研究计划的资助下, 我国首次建立了结合形式化方法、覆盖软件研制全周期、以可信要素为核心的航天嵌入式软件可信保障技术体系以及相应的可信保障集成环境, 并在“嫦娥”等重大工程软件的可信性保障中发挥了重要作用[55].有趣的是, 人们时常在高等级安全标准中通过形式化方法发现其中的错误.例如, 通过形式验证发现了ARINC653 P1-3的6个功能安全问题[223].除了功能安全之外, 面向信息安全的形式化方法应用也受到关注, 几乎所有的形式化方法, 例如定理证明、模型检验、符号执行、抽象解释在软件安全、可信平台等方面都有应用.Subramanyan等人形式化定义了支持可信计算硬件平台(包括Intel SGX和MIT Sactum)的统一抽象模型TAP (trusted abstract platform), 形式化定义了TAP所需要满足的3种关键性质, 并验证了Intel SGX和MIT Sactum与TAP之间的精化关系[224].
根据形式化程度的不同, 形式化方法应用首先要确定是在整个系统应用亦或在关键部分应用.确定了应用的系统范围或边界之后, 可在相关部分中不同程度地应用形式化方法.一个基本要求是, 这些部分都将建立形式规约, 而开发中规约精化过程可以有所区分, 规约与性质的关系可以通过非形式的说明、严格的讨论、形式验证等不同的形式加以论证.质量、生产率和成本是3个相互制约的因素, 形式化方法的应用能够提高软件的可靠性和安全性, 同时, 在当前的技术和工具水平下, 也存在着较大的开销.过度使用形式化方法会使得方法应用的性价比降低, 形式化使用程度需要与费效比有一个权衡, 这与软件工程经济学一样不可忽视.形式化方法的语用很重要, 包括谁来用、使用对象、何时用以及如何用的指南.为提高方法应用的性价比, 在形式化方法研究和应用中, 领域特定的特点比较突出, 往往是应用在部分关键模块, 并使用一些其他方法和形式化方法相结合的轻量级形式化方法.
计算机系统软件自身的可靠性、安全性是整个计算机系统能够正常工作的前提, 因而用形式化方法来验证系统软件、为其可靠性和安全性提供严格保证, 一直是人们长期关注的应用方向.早在20世纪80年代, Moore等人就开展了对CLI软件栈(CLI stack)的形式验证[225].CLI软件栈自上而下包括一个编程语言的编译器、汇编器、链接器、一个多任务的操作系统内核以及硬件体系结构.验证工作涵盖了上述整个软件栈, 并且构造了抽象层次, 使得高层的验证工作基于低层抽象完成, 整个验证工作形成了一个整体.近10多年以来, 基于交互式定理证明的形式化方法在可验证的系统软件上取得显著的突破.这有3方面的因素:一是基础软件在整个信息系统体系中的价值日益提高, 这在一定程度上使得重量级的形式化方法在其上应用的成本变得有可能接受; 二是系统软件与应用软件相比, 其核心部分的边界和功能比较稳定而不多变, 一次验证完成后可以为社区共享; 三是形式验证工具的自动化能力有了明显改善, 并且系统软件也可以作为形式化方法发展的磨刀石.在编译器方面, CompCert始于2005年, 一直持续至今, 形式验证了一个基本上符合ISO-C-90和ANSI-C标准的工业级的C语言编译器, 它可以有效生成PowerPC、ARM和x86处理器上的代码.整个验证工作集中在编译过程核心部分, 涉及了14遍扫描和11种中间语言.CompCert C编译的验证规模在当时是空前的, 该项研究获得了2012年Microsoft Research Verified Software Milestone Award.比较有代表性的操作系统内核验证则包括澳大利亚NICTA对seL4的验证[59]、耶鲁大学团队对CertiKOS的验证[157]、中科大团队对μC/OS-II的验证[226]等.seL4在DARPA HACMS项目实验中, 作为无人机系统OS抵御了信息安全攻击.此外, 还有对分布式系统的验证[227]、安全系统的验证[228, 229]、文件系统的验证[230, 231]等.在系统软件上的成功, 鼓励了形式化方法在计算机全栈系统形式验证的努力.2016年, 美国NSF支持了大规模的探索项目DeepSpec, 拟形成一种形式化方法开发的全栈工具链.
形式化方法不仅能够保证系统软件自身的可靠性和安全性, 它反过来也能为系统结构的优化提供重要启发和支持.微软研究院的Singularity项目团队指出[232, 233]:操作系统中经典的虚拟内存机制其实是一种动态防护机制, 防止一个进程的内存错误或恶意进程会影响内核或者其他进程.然而, 高级程序设计语言的类型安全机制已经能够确保通过类型检查的程序不会发生内存错误, 而且携带证明代码(proof-carrying code, 简称PCC[234])和带类型的汇编语言(typed assembly language, 简称TAL[235])则能确保这种内存安全不仅在源程序上可以保证, 在可执行代码层面依然可以保证.有了这种保证, 我们就不再需要虚拟内存机制所提供的保护, 从而可以减少为实现虚拟内存所做的动态地址翻译带来的运行时开销.
5 形式化方法面临的挑战与未来
具有数学基础的方法或者建立方法的数学基础是工程方法走向成熟、理性的必由之路.从应用上看, 不断增加软件开发的机械化和自动化程度, 提高软件的质量和生产率、尽可能减低成本是工程实践的愿景.尽管形式化方法对于提高软件质量的作用已经形成共识, 但其对大规模软件生产率和成本的影响还没有明确的认识, 对形式化方法的认可度和应用度的进展仍然缓慢.在已有的形式化方法的规模应用中, 使用者大多是有良好形式化方法素养/培训的人员, 甚至是方法、技术和工具本身的研发者.一些软件工程实践表明:除了把程序视作形式规约以外, 工程师们并不愿意大量编写形式规约, 认为形式化方法本身比较复杂, 在某种程度上增加了软件系统的设计复杂度.因此, 形式化方法的首要挑战是发展形式化方法的应用形态, 包括技术形态和工具形态, 提高形式化方法的易用性、有效性和扩展性, 降低形式化方法的应用门槛.
程序设计语言和程序正确性是形式化方法发展的最初源泉.面向程序设计语言和代码, 研究和运用形式化方法、技术与工具是一个重要的方向.人们在实际的程序设计语言上开展了很多验证技术的研究, 围绕程序代码的形式验证技术的发展趋势将会明显, 验证将成为程序设计环境的一部分, 如同程序测试、代码推荐的功能一般.程序设计语言与规约语言的融合将成为趋势.形式化方法的许多思想和方法在程序设计语言的设计中有重要的影响.许多新型程序设计语言设计之初的想法和应用源自于形式化方法.Rust语言[236]的成功是形式化方法研究对系统开发提供支持的代表性案例, 它主要面向系统编程:一方面, 语言支持并发以及手工内存分配和释放; 另一方面, 语言借鉴类型系统、线性逻辑和并发分离逻辑的思想, 在语言中引入内存所有权(ownership)以及所有权传递(ownership transfer)的概念, 避免了内存错误以及并发程序中常见的数据竞争错误.目前, Rust语言受到了工业界和学术界的广泛关注, 已有多个使用Rust开发的较有影响力的系统, 包括浏览器、操作系统和其他各种工具.与这一趋势相伴, 对可视化编程机制以及领域相关特性的支持, 将进一步推动新型语言的可用性和可行性.
近10年来, 形式化方法进入一个振兴的阶段.无论是轻量级的形式化方法与主流方法的结合, 还是重量级的形式化方法在工业级软件上的应用, 都取得了较大的进步和成功[237].在这些成功应用的后面, 工具起到了决定性的作用.系统一旦使用了形式规约语言建模, 它就能用工具进行语义分析.工具也缓解了问题规模带来的压力.因此, 构建更加可用和鲁棒的工具支持大规模规约的并行语义分析和验证, 构建可复用的形式规约库和方法社区, 推动形式化方法工具和可复用库设施的进步, 包括工具的集成、工具的无形化、规约与验证资产, 毫无疑问都会是形式化方法努力的方向.
规约、开发和验证的系统与环境的形态变化是形式化方法发展的驱动力.形式化方法的目标在于高质量的描述、开发和确认软件系统, 因而软/硬件的形态进步和地位的变化对形式化方法有着直接的影响.例如, 形式化方法发展的一条重要线索是从顺序程序到并行程序、混成系统、信息物理融合系统乃至人机物融合系统, 而人机物融合社会中混成系统对形式化方法的基础、方法、技术和工具都形成了全面的挑战[238, 239].
软件正在成为社会基础设施, 而形式化方法在计算机系统基础软/硬件的可靠性中发挥了十分重要的作用, 这正是人们最能认识到的形式化方法在关键的信息基础设施中发挥作用的应用点.在软件基础设施方面, 全栈的可验证软件将会持续地进展, 并有可能在实用主流操作系统中逐渐地渗透.例如, 为了保证云服务基础设施的可靠性, Amazon利用TLA+方法对其S3云存储服务的关键算法进行了形式验证, 发现了不少缺陷[240].2017年, Linux基金会宣称, 将对一些Linux内核模块进行形式验证以提高系统的安全性[241].基于形式化方法的信息安全性研究毫无疑问是一个方向[242].面向未来的软件基础设施, 区块链和智能合约的正确性及信息安全性验证正蓬勃展开[243, 244].
在软件定义一切的时代, 形式化方法将定义软件.形式化方法如何与其他软件开发方法、领域特定的融合显得尤为重要.对应于软件定义时代的软件形态的特征变化、质量的需求变化, 形式化方法需要在基础概念、规约、开发和验证技术与工具上适应更为复杂开放、动态多变、持续演化的软件形态.例如, 在人机物融合下, 需要准确、恰当地处理非形式化需求到形式规约、形式化抽象到非形式化场景和现实世界的边界建模, 大量非功能规约包括社会化人因的规约, 自主自适应自组织等新型软件结构和行为的规约、推理与验证等等.在形式化方法的发展中, 数学与形式化方法有着密切的互动, 数学为形式化模型和推理提供了基础, 而形式化方法也促进了数学的发展.形式化方法可以机械、高效、准确无误地写出复杂数学问题的可靠证明, 甚至帮助解决一些长期悬而未决的数学难题, 例如四色定理[245]、罗宾斯猜想(Robbins conjecture)[246]、开普勒猜想(Kepler conjecture)[247](该原始证明超过300多页, 正式发表的证明也近130页, 其正确性无法保证[248])等等.形式化(工程)数学[249]对于构建高可信智能制造软件环境也具有重要价值.
形式化方法和人工智能有着密切的联系.定理证明和约束求解是符号主义流派人工智能的重要内容.如何利用人工智能的其他成果提高形式化方法的水平是一个值得关注的方向, 例如基于机器学习帮助构建形式规约、发现不变式或者推荐证明策略辅助形式验证、辅助规约精化和程序综合等等.程序综合与机器学习交叉, 出现了基于深度学习和框架生成相结合的程序综合方法.另一方面, 机器学习软件也是程序, 研究它们的形式化方法是非常有价值的[250, 251].例如, 概率程序设计的形式语义、验证和调试、大数据处理程序的验证、深度学习程序的形式规约与鲁棒性验证、利用形式化方法建立更好的训练方法、研究机器学习的可解释性, 都是值得探索的课题.
在新的计算模型方面, 量子程序设计[252]的理论成为了形式化方法发展的新内容.形式化方法已经应用到了量子程序设计语言的语义分析、关键性质的推理, 也出现了量子计算的程序逻辑和模型检验方法.由于量子程序和传统程序相比有很大的不同, 特别是由于量子叠加和纠缠的存在, 建立系统的量子计算的形式化方法并开发有效的验证技术才刚刚起步.
计算思维的渗透性也带动了形式化方法与其他学科的交叉融合, 例如在生物研究领域, 计算建模和分析已经成为一种重要方法[253], 例如Naïve T cell differentiation的时序行为建模和分析[254].这些研究有力地促进了混成系统形式化方法的发展, 也促进了医疗生命科学的发展, 并为医工结合交叉提供了一个明确的方向[255].
教育是形式化方法持续发展的重要推手.受限于可用性和可扩展性, 形式化方法学习曲线长, 高强度运用需要较高的门槛, 严重制约了形式化方法在软件开发中的广泛应用.而计算系统的可信愈来愈重要, ACM和IEEE制定的计算机科学和软件工程课程计划都包含了程序正确性的内容[256, 257].我国的形式化方法教育现状调查结果指出, 需要加强专业教育中形式化方法认知[258].形式化方法的轻量级运用已经能够显著提高人们对系统需求和设计的理解, 而且程序就是一种形式规约, 可以机械化自动地处理(编译或执行).形式化方法对于软件开发人员而言实际上都在接触, 只是形式化程度不同而已.因而在计算思维养成过程中, 在程序设计、数据结构等基础课增加形式化概念的讨论, 在离散数学、算法、软件工程等后续专业课程突出形式化方法与主流方法的关系和结合, 对于形式化方法的推广和水平提高是非常重要的.
6 结束语
形式化方法可以严格分析、处理、证明计算机系统和程序及其性质, 对于确保系统正确性和提高可信性具有基础性的作用.形式化方法的应用已经取得了长足的进步, 实践证实, 其在大规模程序设计中起到了一个直接的指导作用, 提供了形式化开发的概念框架和基本理解, 促进了目前的最佳实践, 其成果深刻影响了未来软件学科的发展方向[259].同时, 形式化方法需要适应软件定义使能的软件新形态, 适应软件作为社会基础设施的地位, 在基础概念、规约、验证和工具等方面进一步发展, 并与人工智能、网络空间安全、量子计算、生物计算等领域和方向交叉、融合.