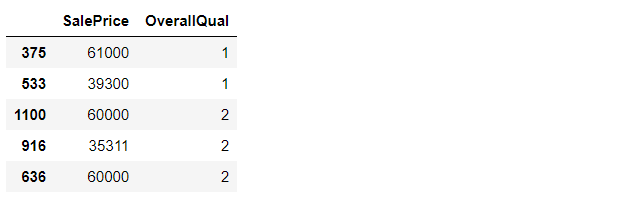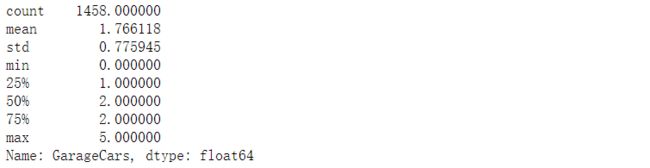Kaggle房价预测详解
Kaggle房价预测详解
-
-
- 1.导入数据
- 2.查看各项主要特征与房屋售价的关系
-
- 查看中央空调与售价关系
- 查看装修水平与房价关系
- 查看建造日期与售价关系
- 不同地段与房价关系
- 查看地皮面积与房价关系
- 查看地下室总面积与房价关系
- 查看关联性
- 3.训练集数据预处理
-
- 训练数据预处理
- 创建机器学习模型
- 得出预测结果
- 4.导入测试集数据
-
- 测试集数据预处理
- 创建训练集特征值
- 得到预测数据
- 4.保存预测结果
-
1.导入数据
导入库
# 导入需要的模块
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
# 离散统计分布以及连续统计分布
from scipy import stats
# 正态分布
from scipy.stats import norm
# 数据标准化
from sklearn.preprocessing import StandardScaler
# 消除红色警告
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
导入数据
https://pan.baidu.com/s/1bugy1D4YKSJjOnns5_YZXA
提取码:x13i
# 导入训练数据
data_train = pd.read_csv("E:/PythonData/machine_learning/train.csv")
# 查看训练数据(前5行数据)
data_train.head()
2.查看各项主要特征与房屋售价的关系
查看房子售价统计信息
# 查看房子售价的统计信息
data_train['SalePrice'].describe()
data_train.isnull().sum()
# 绘制密度曲线
sns.distplot(data_train['SalePrice'])
plt.show()
# 计算房价的峰度和偏度
SP_skew = data_train['SalePrice'].skew()
SP_kurt = data_train['SalePrice'].kurt()
print('峰度:',SP_skew)
print('偏度:',SP_kurt)
峰度(Kurtosis)是描述某变量所有取值分布形态陡缓程度的统计量。
它是和正态分布相比较的。
Kurtosis=0 与正态分布的陡缓程度相同。
Kurtosis>0 比正态分布的高峰更加陡峭——尖顶峰
Kurtosis<0 比正态分布的高峰来得平台——平顶峰计算公式:β = M_4 /σ^4 偏度:
偏度:
偏度(Skewness)是描述某变量取值分布对称性的统计量。
Skewness=0 分布形态与正态分布偏度相同
Skewness>0 正偏差数值较大,为正偏或右偏。长尾巴拖在右边。
Skewness<0 负偏差数值较大,为负偏或左偏。长尾巴拖在左边。 计算公式: S= (X^ - M_0)/δ Skewness 越大,分布形态偏移程度越大。
分析:
将上面的计算结果、理论和图形相对比可以看到,长尾巴确实拖在右边,而且高峰陡峭。
查看中央空调与售价关系
# CentralAir;是否有中央空调
var = 'CentralAir'
data1 = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
fig = sns.boxplot(x=var, y="SalePrice", data=data1)
fig.axis(ymin=0, ymax=800000);
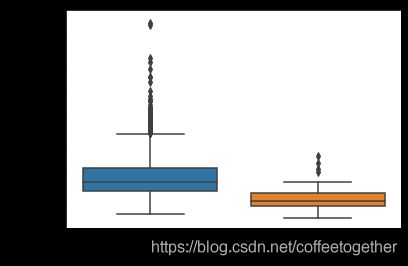
查看装修水平与房价关系
1. 绘制装修水平与房价箱线图
# OverallQual 房子材料与装修水平
var = 'OverallQual'
data2 = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
fig = sns.boxplot(x=var, y="SalePrice", data=data2)
fig.axis(ymin=0, ymax=800000);
data2 = data[["SalePrice","OverallQual"]].sort_values(by="OverallQual",ascending=True)
data2.head()
data2 = data[["SalePrice","OverallQual"]].sort_values(by="OverallQual",ascending=True)
data2.head()
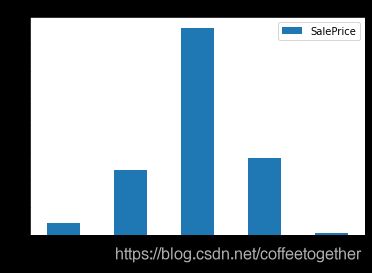
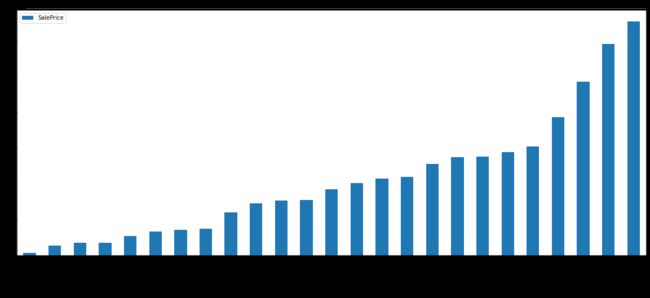
O_S = data2[['OverallQual','SalePrice']].groupby(['OverallQual']).sum().sort_values(by='OverallQual',ascending=True)
O_S.plot(kind='bar')
plt.show()

分析:由上图,房价随着装修水平的提升也逐渐提升。而根据柱状图可知:在装修水平为6-7时房价的销售额最对。即6-7水平的房间卖得最火。
查看建造日期与售价关系
# YearBuilt boxplot 房子建造日期
data3 = pd.concat([data_train['SalePrice'], data_train'YearBuilt']], axis=1)
data3.head()
plt.scatter(data3['YearBuilt'],data1['SalePrice'])
plt.show()
Y_S = data3[['YearBuilt','SalePrice']].groupby(['YearBuilt']).sum().sort_values(by='YearBuilt',ascending=True)
Y_S.plot()
plt.show()
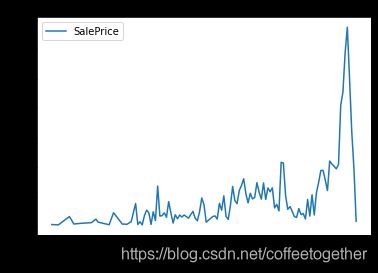
总结:房子售价随着年份的推移越来越高。2005年左右房价销售额达到顶峰。
不同地段与房价关系
绘制不同地段与房价箱线图
# Neighborhood 地段与售价关系
var = 'Neighborhood'
data4 = pd.concat([data_train['SalePrice'], data_train[var]], axis=1)
f, ax = plt.subplots(figsize=(26, 12))
fig = sns.boxplot(x=var, y="SalePrice", data=data4)
fig.axis(ymin=0, ymax=800000);
N_S = data4[['Neighborhood','SalePrice']].groupby(['Neighborhood']).sum().sort_values(by='SalePrice',ascending=True)
N_S.plot(kind='bar',figsize=(20,8))
plt.show()
分析:由上图,CollgCr地段与NAmes地段房子销售额最高。
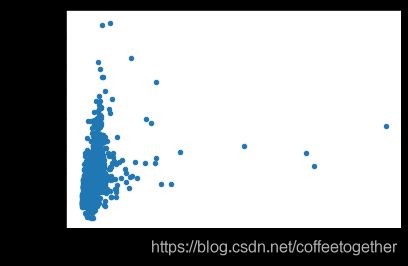
查看地皮面积与房价关系
# 地皮面积与售价散点图
# 创建售价与地皮面积表格
data5 = pd.concat([data_train['SalePrice'], data_train['LotArea']], axis=1)
data5.plot.scatter(x='LotArea' , y='SalePrice', ylim=(0, 800000))
plt.show()
# 绘制生活面积与售价散点图
data6 = pd.concat([data_train['SalePrice'], data_train['GrLivArea']], axis=1)
data6.plot.scatter(x='GrLivArea', y='SalePrice', ylim=(0, 800000))
plt.show()
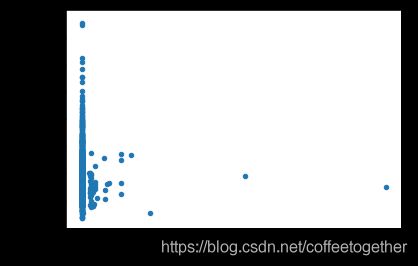
查看地下室总面积与房价关系
绘制地下室总面积与房价散点图
# 地下室总面积与售价散点图
data7 = pd.concat([data_train['SalePrice'], data_train['TotalBsmtSF']], axis=1)
data7.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))
plt.show()
# 绘制其他资产与售价散点图
data8 = pd.concat([data_train['SalePrice'], data_train['MiscVal']], axis=1)
data8.plot.scatter(x='MiscVal', y='SalePrice', ylim=(0, 800000))
plt.show()
# 绘制车库与售价散点图
var = ['GarageArea', 'GarageCars']
data9 = pd.concat([data_train['SalePrice'], data_train[var[0]]], axis=1)
data9.plot.scatter(x=var[0], y='SalePrice', ylim=(0, 800000))
plt.show()
data10 = pd.concat([data_train['SalePrice'], data_train[var[1]]], axis=1)
GC_S = data10.groupby(data10['GarageCars']).sum().sort_values(by='GarageCars',ascending=True)
GC_S.plot(kind='bar')
plt.xticks(rotation=360)
plt.show()
查看关联性
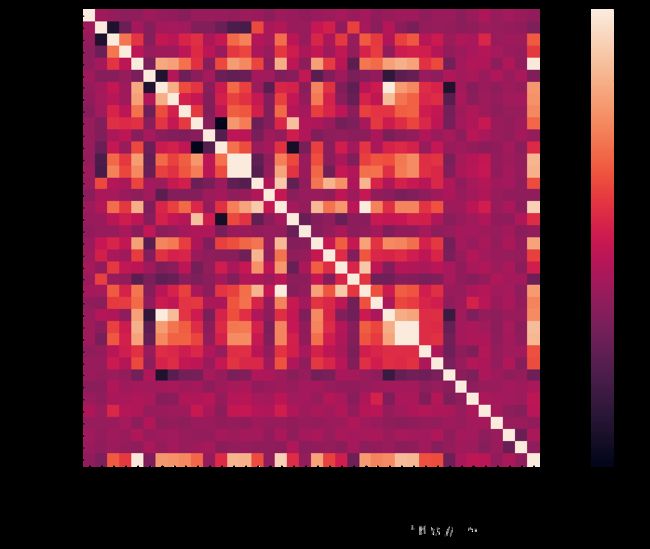
# 查看关联性
corrmat = data_train.corr()
f, ax = plt.subplots(figsize=(20, 9))
sns.heatmap(corrmat, vmax=0.8, square=True)
from sklearn import preprocessing
f_names = ['CentralAir', 'Neighborhood']
for x in f_names:
label = preprocessing.LabelEncoder()
data_train[x] = label.fit_transform(data_train[x])
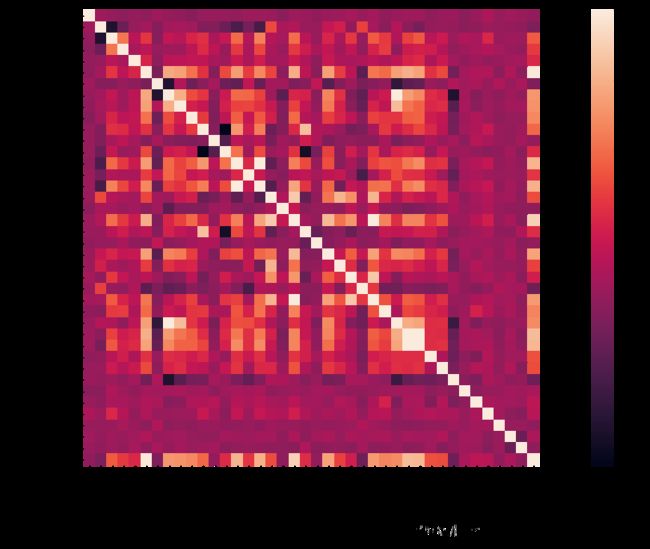
corrmat = data_train.corr()
f, ax = plt.subplots(figsize=(20, 9))
sns.heatmap(corrmat, vmax=0.8, square=True)
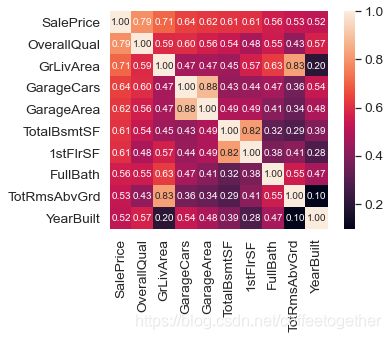
# 关系矩阵中将显示10个特征
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(data_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, \
square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
3.训练集数据预处理
训练数据预处理
# 数据预处理
from sklearn import preprocessing
# 导入机器学习模型最小二乘法,支持向量机,高斯分布
from sklearn import linear_model, svm, gaussian_process
# 导入机器学习随机森林
from sklearn.ensemble import RandomForestRegressor
# 划分数据
from sklearn.model_selection import train_test_split
import numpy as np
选取特征数据(将数据转换成转换成正态分布)
# 获取数据
# 一共7个特征数据
cols = ['OverallQual','GrLivArea', 'GarageCars','TotalBsmtSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt']
x = data_train[cols].values
y = data_train['SalePrice'].values
# fit_transform不仅计算训练数据的均值和方差,还会基于计算出来的均值和方差来转换训练数据,从而把数据转换成标准的正太分布
# 将x数据转换成正态分布
x_scaled = preprocessing.StandardScaler().fit_transform(x)
y_scaled = preprocessing.StandardScaler().fit_transform(y.reshape(-1,1))
# 分割数据,测试集展1/3
X_train,X_test, y_train, y_test = train_test_split(x_scaled, y_scaled, test_size=0.33, random_state=42)
创建机器学习模型
创建字典,分别创建三个模型
# 创建字典,分别创建三个模型
clfs = {
'svm':svm.SVR(),
'RandomForestRegressor':RandomForestRegressor(n_estimators=400),
'BayesianRidge':linear_model.BayesianRidge()
}
# 分别对3个模型记性训练,并得出预测结果误差
for clf in clfs:
try:
clfs[clf].fit(X_train, y_train)
y_pred = clfs[clf].predict(X_test)
print(clf + " cost:" + str(np.sum(y_pred-y_test)/len(y_pred)) )
except Exception as e:
print(clf + " Error:")
print(str(e))

分析:随机森林得到的结果误差相对时最小的。
再次创建特征参数
# 创建特征列表
cols = ['OverallQual','GrLivArea', 'GarageCars','TotalBsmtSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt']
# 将特征值赋值给x
x = data_train[cols].values
# 将房价结果赋值给y
y = data_train['SalePrice'].values
# 将训练数据2/3作为训练集,1/3作为测试集
X_train,X_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=42)
clf = RandomForestRegressor(n_estimators=400)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
得出预测结果
# 显示预测结果
y_pred[::5]
# 显示测试集结果
y_test[::5]
4.导入测试集数据
测试集数据预处理
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
# 之前训练的模型
rfr = clf
# 导入测试集数据
data_test = pd.read_csv("E:/PythonData/machine_learning/test.csv")
处理测试集数据缺失值
# 查看缺失值情况
data_test[cols].isnull().sum()
# 查看统计情况
data_test['GarageCars'].describe()
data_test['TotalBsmtSF'].describe()
创建训练集特征值
# 创建5个特征值
cols2 = ['OverallQual','GrLivArea', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt']
# 缺失值处理,利用对应字段的平均值填充缺失值
cars = data_test['GarageCars'].fillna(1.766118)
bsmt = data_test['TotalBsmtSF'].fillna(1046.117970)
# 横向合并
data_test_x = pd.concat( [data_test[cols2], cars, bsmt] ,axis=1)
data_test_x.isnull().sum()
x = data_test_x.values
y_te_pred = rfr.predict(x)
print(y_te_pred)
print(y_te_pred.shape)
print(x.shape)
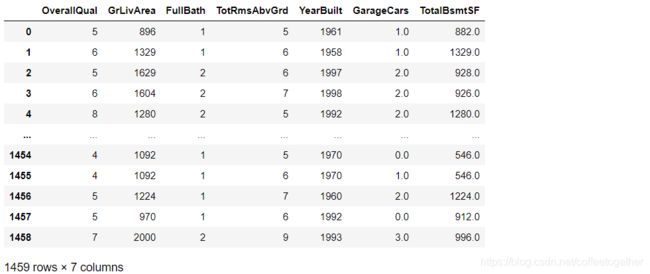
data_test_x
得到预测数据
prediction = pd.DataFrame(y_te_pred, columns=['SalePrice'])
result = pd.concat([ data_test['Id'], prediction], axis=1)
# result = result.drop(resultlt.columns[0], 1)
result.head()
4.保存预测结果
# 保存预测结果
result.to_csv('E:/PythonData/machine_learning/Predictions1.csv', index=False)
注:先将训练集划分成2/3的训练集和测试集。通过不同的训练模型对其进行训练学习,得出每个训练模型的误差。用误差最小的随机森林模型对测试集数据进行训练,得出预测结果。