内存高效的可逆 GAN 网络:Reversible GANs for Memory-efficient Image-to-Image Translation
Reversible GANs for Memory-efficient Image-to-Image Translation
[pdf]
目录
Abstract
Introduction
Background and Related Work
Method
Abstract
The Pix2pix [17] and CycleGAN [40] losses have vastly improved the qualitative and quantitative visual quality of results in image-to-image translation tasks.
We extend this framework by exploring approximately invertible architectures which are well suited to these losses.
These architectures are approximately invertible by design and thus partially satisfy cycle-consistency before training even begins. Furthermore, since invertible architectures have constant memory complexity in depth, these models can be built arbitrarily deep.
We are able to demonstrate superior quantitative output on the Cityscapes and Maps datasets at near constant memory budget.
Pix2pix 和 CycleGAN 损失,极大地改善了图像到图像转换任务中结果的视觉质量。本文扩展了这个框架,探索了近似可逆的体系结构,它非常适合这些损失。这些架构在设计上是近似可逆的,因此在训练开始之前就部分地满足了周期一致性。此外,由于可逆体系结构在深度上具有恒定的存储复杂性,这些模型可以建立任意深度。我们能够在接近恒定内存预算的情况下,在 Cityscapes 和 Maps 数据集上展示卓越的输出。
Introduction
Computer vision was once considered to span a great many disparate problems, such as superresolution [12], colorization [8], denoising and inpainting [38], or style transfer [14]. Some of these challenges border on computer graphics (e.g. style transfer), while others are more closely related to numerical problems in the sciences (e.g. superresolution of medical images [35]). With the new advances of modern machine learning, many of these tasks have been unified under the term of image-to-image translation [17].
背景介绍:图像翻译任务
计算机视觉曾经被认为跨越了许多不同的问题,如超分辨率,着色,去噪,恢复,风格转移[14]。其中一些挑战接近于计算机图形学 (如风格转换),而另一些则更接近于科学中的数值问题 (如医学图像的超分辨率)。随着现代机器学习的新进展,许多任务被统一为图像到图像的翻译。
Mathematically, given two image domains X and Y , the task is to find or learn a mapping F : X → Y , based on either paired examples {(xi , yi)} or unpaired examples {xi} ∪ {yj}. Let’s take the example of image superresolution. Here X may represent the space of low-resolution images, and Y would represent the corresponding space of high-resolution images. We might equivalently seek to learn a mapping G : Y → X. To learn both F and G it would seem sufficient to use the standard supervised learning techniques on offer, using convolutional neural networks (CNNs) for F and G.
For this, we require paired training data and a loss function
to measure performance. In the absence of paired training data, we can instead exploit the reciprocal relationship between F and G. Note how we expect the compositions G ◦ F
Id and F ◦ G
Id, where Id is the identity. This property is known as cycle-consistency [40]. The unpaired training objective is then to minimize
(G◦F(x), x) or
(F ◦G(y), y) with respect to F and G, across the whole training set. Notice how in both of these expressions, we never require explicit pairs (xi , yi). Naturally, in superresolution exact equality to the identity is impossible, because the upsampling task F is one-to-many, and the downsampling task G is many-to-one.
本文算法提出的思路过程:
给定两个图像域 X 和 Y,任务是根据成对的例子 {(xi, yi)} 或未成对的例子 {xi} ∪ {yj} 找到或学习映射 F: X→Y。以图像超分辨率为例。这里 X 可以表示低分辨率图像的空间,Y 表示高分辨率图像对应的空间。寻求学习映射 G: Y→X。使用标准的监督学习技术,如利用卷积神经网络 (CNN) ,学习两个 F 和 G 似乎很难。
为此,需要成对训练数据和损失函数 ![]() 测量性能。在没有成对训练数据的情况下,可以利用 F 和 G 之间的互相关系(reciprocal relationship)。注意,我们期望组合 G◦F
测量性能。在没有成对训练数据的情况下,可以利用 F 和 G 之间的互相关系(reciprocal relationship)。注意,我们期望组合 G◦F ![]() Id 和 F◦G
Id 和 F◦G ![]() Id,其中Id是恒等式(identity)。这个特性被称为循环一致性。非配对的训练目标是在整个训练集,最小化
Id,其中Id是恒等式(identity)。这个特性被称为循环一致性。非配对的训练目标是在整个训练集,最小化 ![]() (G◦F(x), x) 或
(G◦F(x), x) 或 ![]() (F◦G(y), y) 。注意,在这两个表达式中,不需要显式的数据对 (xi, yi)。当然,在超分辨率中不可能与恒等式完全相等,因为上采样任务 F 是一对多的,而下采样任务 G 是多对一的。
(F◦G(y), y) 。注意,在这两个表达式中,不需要显式的数据对 (xi, yi)。当然,在超分辨率中不可能与恒等式完全相等,因为上采样任务 F 是一对多的,而下采样任务 G 是多对一的。
The problem with the cycle-consistency technique is that while we can insert whatever F and whatever G we deem appropriate into the model, we avoid making use of the fact that F and G are approximate inverses of one another. In this paper, we consider constructing F and G as approximate inverses, by design. This is not a replacement to cycleconsistency, but an adjunct to it.
A key benefit of this is that we need not have a separate X → Y and Y → X mapping, but just a single X → Y model, which we can run in reverse to approximate Y → X.
Furthermore, note by explicitly weight-tying the X → Y and Y → X models, we can see that training in the X → Y direction will also train the reverse Y → X direction, which does not necessarily occur with separate models.
Lastly, there is also a computational benefit that invertible networks are very memory-efficient [15]; intermediate activations do not need to be stored to perform backpropagation. As a result, invertible networks can be built arbitrarily deep, while using a fixed memory-budget—this is relevant because recent work has suggested a trend of wider and deeper networks performing better in image generation tasks [4]. Furthermore, this enables dense pixel-wise translation models to be shifted to memory-intensive arenas, such as 3D (see Section 5.3 for our experiements on dense MRI superresolution).
本文方法的优点:
循环一致性技术的问题是,虽然我们可以插入任何我们认为合适的 F 和 G 到模型中,但我们避免使用 F 和 G 是彼此近似的倒数这一事实。在本文中,我们考虑通过设计来构造近似逆函数 F 和 G。这不是循环一致性的替代,而是它的补充。
一个关键的好处是我们不需要一个单独的 X→Y 映射,只需要一个 X→Y 模型,我们可以运行在反向近似 Y→X 。
此外,注意通过显式地 weight-tying X→Y 和 Y→X 模型,我们可以看到,在训练 X→Y 方向时还训练反向 Y→X 方向,这在单独的模型中不一定会发生。
最后,还有一个计算上的好处,可逆网络的内存效率非常高;执行反向传播时不需要存储中间激活。因此,当使用固定的内存预算时,可逆网络可以构建任意深度——这是相关的,因为最近的研究表明,在图像生成任务中,更宽、更深的网络表现得更好。此外,这使得密集像素转换模型可以转移到内存密集的领域,如 3D (见 5.3 节关于密集 MRI 超分辨率的实验)。
Our results indicate that by using invertible networks as the central workhorse in a paired or unpaired image-to-image translation model such as Pix2pix [17] or CycleGAN [40], we can not only reduce memory overhead, but also increase fidelity of the output. We demonstrate this on the Cityscapes and Maps datasets in 2D and on a diffusion tensor image MRI dataset for the 3D scenario (see Section 5).
实验结果:
我们的结果表明,在成对或不成对的图像到图像转换模型 (如 Pix2pix[17] 或 CycleGAN[40]) 中,使用可逆网络作为中心 workhorse,不仅可以减少内存开销,而且还可以提高输出保真度。我们在 2D 的 Cityscapes 和 Maps 数据集以及 3D 场景的扩散张量图像 MRI 数据集上展示了这一点 (参见第5节)。
Background and Related Work
Invertible Neural Networks (INNs)
In recent years, several studies have proposed invertible neural networks (INNs) in the context of normalizing flow-based methods [33] [23]. It has been shown that INNs are capable of 1)generating high quality images [22], 2)perform image classification without information loss in the hidden layers [18] and 3)analyzing inverse problems [1]. Most of the work on INNs, including this study, heavily relies upon the transformations introduced in NICE [10] later extended in RealNVP [11]. Although INNs share interesting properties they remain relatively unexplored.
近年来,在基于归一化流的方法的背景下,一些研究提出了可逆神经网络 (INNs)。研究表明,INNs 能够生成高质量的图像,能够在不丢失信息的隐层中进行图像分类,能够分析逆问题。大多数关于 INN 的工作,包括本研究,都严重依赖于 NICE[10] 中和 RealNVP[11]。尽管客栈拥有一些有趣的特性,但它们仍相对未被发掘。
[10] NICE: Non-linear independent components estimation. [2015 ICLR]
[11] Density estimation using Real NVP. [2017 ICLR]
Additive Coupling
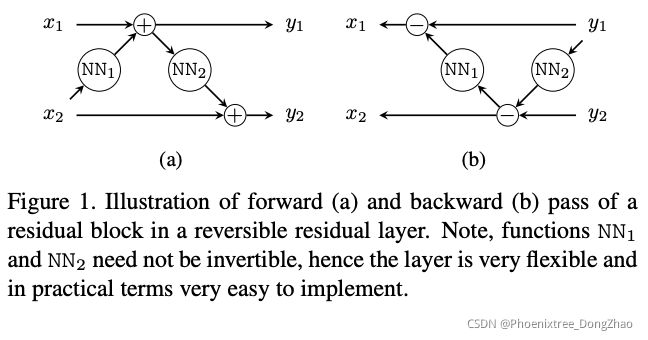
In our model, we obtain an invertible residual layer, as used in [15], using a technique called additive coupling [10]: first we split an input x (typically over the channel dimension) into (x1, x2) and then transform them using arbitrary complex functions NN1 and NN2 (such as a ReLU-MLPs) in the form (left):
The inverse mappings can be seen on the right. Figure 1 shows a schematic of these equations.
耦合(Coupling)
在本文模型中,使用一种称为 additive coupling 来获得一个可逆的残差层。首先,将一个输入 x (通常在频道维度) 到 (x1, x2),然后把它们使用任意复杂函数 NN1 和 NN2 (方程(8)和(9)左的形式 (如 ReLU-MLPs))。
公式右边是逆映射。图 1 显示了这些方程的示意图。
Memory efficiency
Interestingly, invertible residual layers are very memory-efficient because intermediate activations do not have to be stored to perform backpropagation [15]. During the backward pass, input activations that are required for gradient calculations can be (re-)computed from the output activations because the inverse function is accessible. This results in a constant spatial complexity (O(1)) in terms of layer depth (see Table 1).
有趣的是,可逆剩余层的内存效率非常高,因为执行反向传播时不需要存储中间激活。在向后传递期间,梯度计算所需的输入激活可以从输出激活 (重新) 计算,因为逆函数是可访问的。这导致在层深度方面具有恒定的空间复杂性 (O(1))(见表1)。
Method
Our goal is to create a memory-efficient image-to-image translation model, which is approximately invertible by design. Below we describe the basic outline of our approach of how to create an approximately-invertible model, which can be inserted into the existing Pix2pix and CycleGAN frameworks. We call our model RevGAN.
我们的目标是创建一个内存效率高的图像-图像转换模型,该模型设计为近似可逆的。下面我们描述了如何创建近似可逆模型的基本轮廓,该模型可以插入到现有的 Pix2pix 和 CycleGAN 框架中。我们称我们的模型为 RevGAN。
Lifting and Projection
In general, image-to-image translation tasks are not one-to-one. As such, a fully invertible treatment is undesirable, and sometimes in the case of dimensionality mismatches, impossible.
Furthermore, it appears that the high-dimensional, overcomplete representations used by most modern networks lead to faster training [29] and better all-round performance [4].
We therefore split the forward F : X → Y and backward G : Y → X mappings into three components. With each domain, X and Y , we associate a high-dimensional feature space X˜ and Y˜ , respectively. There are individual, noninvertible mappings between each image space and its corresponding high-dimensional feature-space; for example, for image space X we have Enc_X : X → X˜ and Dec_X : X˜ → X. Enc_X lifts the image into a higher dimensionality space and Dec_X projects the image back down into the lowdimensional image space. We have used the terms encode and decode in place of ‘lifting’ and ‘projection’ to stay in line with the deep learning literature.
通常,图像到图像的转换任务不是一对一的。因此,完全可逆处理是不可取的,有时在维度不匹配的情况下,是不可能的。
此外,似乎大多数现代网络所使用的高维、过完备表示导致更快的训练和更好的全面性能。
因此,我们将前向 F: X→Y 和后向 G: Y→X 映射分成三个组件。在每个域 X 和 Y 中,我们分别关联一个高维特征空间 X˜ and Y˜ 。Enc_X 将图像提升到更高维度的空间,Dec_X 将图像投影回低维度的图像空间。每个图像空间与其对应的高维特征空间之间存在独立的、不可逆转的映射;例如,对于图像空间 X,我们有 Enc_X: X→X˜ 和 Dec_X: X˜→X。我们用 “编码” 和 “解码” 来代替 “提升” 和 “投射”,以保持与深度学习文献一致。
Invertible core
Between the feature spaces, we then place an invertible core C : X˜ → Y˜ , so the full mappings are
For the invertible cores we use invertible residual networks based on additive coupling as in [15]. The full mappings F and G will only truly be inverses if Enc_X ◦ Dec_X = Id and Enc_Y ◦ DecY = Id, which cannot be true, since the image spaces are lower dimensional than the feature spaces. Instead, these units are trained to be approximately invertible pairs via the end-to-end cycle-consistency loss. Since the encoder and decoder are not necessarily invertible they can consist of non-invertible operations, such as pooling and strided convolutions.
在特征空间之间,我们放置一个可逆的核心 C: X˜ → Y˜ ,因此完整的映射为方程 (10) 和 (11)。
对于可逆性核 (invertible cores),我们使用了基于可加耦合 (additive coupling) 的可逆性残差网络。对于 如果 Enc_X◦Dec_X = Id,完整的映射 F 和 G 是可逆的,但对于 Enc_Y◦Dec_Y = Id,是不可逆的,因为图像空间比特征空间低维。相反,这些单元通过端到端周期一致性损失被训练成近似可逆对。由于编码器和解码器不一定是可逆的,它们可以由不可可逆的操作组成,如池化和跨步卷积。
Because both the core C and its inverse C^{−1} are differentiable functions (with shared parameters), both functions can both occur in the forward-propagation pass and are trained simultaneously. Indeed, training C will also train C^{−1} and vice versa. The invertible core essentially weight-ties in the X → Y and Y → X directions.
因为 core C 和它的逆 C^{−1} 都是可微函数 (具有共享参数),这两个函数都可以在前向传播过程中发生并同时被训练。事实上,训练 C 也将训练 C^{−1},反之亦然。可逆性 core 本质上是在 X→Y和 Y→X 方向上的权重捆绑 (weight-ties)。
Given that we use the cycle-consistency loss it may be asked, why do we go to the trouble of including an invertible network? The reason is two-fold:
firstly, while image-to-image translation is not a bijective task, it is close to bijective. A lot of the visual information in an image x should reappear in its paired image y, and by symmetry a lot of the visual information in the image y should appear in x. It thus seems sensible that the networks F and G should be at least initialized, if not loosely coupled to be weak inverses of one another. If the constraint of bijection is too high, then the models can learn to diverge from bijection via the non-invertible encoders and decoders.
Secondly, there is a potent argument for using memory efficient networks in these memory-expensive, dense, pixel-wise regression tasks. The use of two separate reversible networks is indeed a possibility for both F and G. These would both have constant memory complexity in depth. Rather than having two networks, we can further reduce the memory budget by a rough factor of about two by exploiting the loose bijective property of the task, sharing the X → Y and Y → X models.
既然我们使用了周期一致性损失,我们可能会问,为什么要麻烦地加入可逆网络呢?原因有二:
首先,图像翻译不是一个双射任务,但它接近于双射任务。大量的视觉信息在图像 x 应该出现在其配对的图像 y,以及对称图像中大量的视觉信息 y 应该出现在 x。因此似乎合理的网络 F 和 G 至少应该初始化,如果不是松散耦合弱逆。如果双射约束过高,则模型可通过非可逆编码器和译码器学习偏离双射。
其次,在这些内存昂贵、密集、像素化的回归任务中使用内存高效网络是有说服力的。对于 F 和 G 来说,确实有可能使用两个独立的可逆网络。这两个网络在深度上都具有恒定的存储复杂性。与其拥有两个网络,我们还可以通过利用任务的松散双目标特性,共享 X→Y 和 Y→X 模型,进一步将内存预算减少约 2 个粗略因子。
Paired RevGAN
We train our paired, reversible, imageto-image translation model, using the standard Pix2pix loss functions of Equation 4 from [17], applied in the X → Y and Y → X directions:
We also experimented with extra input noise for the conditional GAN, but found it not to help.
在 X→Y 和 Y→X 方向上,我们使用公式 (4) 的标准 Pix2pix 损失函数训练成对的可逆图像-图像平移模型,具体为公式 (12)。
我们还实验了条件 GAN 的额外输入噪声,但发现它没有帮助。
Unpaired RevGAN
For unpaired RevGAN, we adapt the loss functions of the CycleGAN model [40], by replacing the L1 loss with a cycle-consistency loss, so the total objective is:
对于未配对的 RevGAN,我们采用 CycleGAN 模型的损失函数,将 L1 损失替换为周期一致性损失,因此总目标为公式 (13)。