java灰度图像增强_数字图像处理——图像增强
图像增强
图像增强的目的是:改善图像的视觉效果或使图像更适合于人或机器的分析处理
$$ 图像增强 \begin{cases} 空域法 \begin{cases} 点操作 \begin{cases} 直接灰度变换\ 直方图修正 \end{cases}\ 邻域操作 \begin{cases} 图像平滑\ 图像锐化 \end{cases} \end{cases}\ 频域法 \begin{cases} 低通滤波\ 高通滤波 \end{cases} \end{cases} $$
点操作
直接灰度变换
$g(x,y)=T[f(x,y)]$
$T$ => 灰度映射函数
坐标位置 $(x,y)$ 为 $f$ 的自变量,表示当前灰度值,经过函数$T$ 转变为$g$, 注意在T函数中$f(x,y)$为其自变量
直接灰度变换又可以分为:
线性变换
分段线性变换
非线性变换
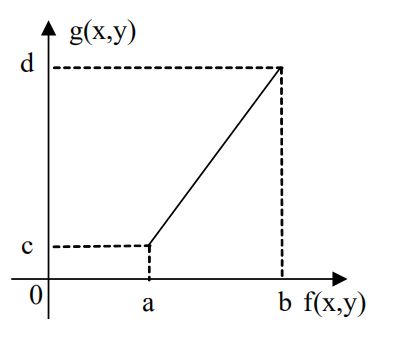
线性变换 & 分段线性变换
对于$f(x,y)$灰度范围为$[a,b]$的部分,进行线性变换
$$g(x,y) = {d-c\over b-a}[f(x,y)-a]+c$$
我们可以用它来做什么?
举个简单的例子,我们可以很容易的通过调整灰度分布,使得图片白的部分更白,黑的部分更黑
void increase(Mat &inputImage, Mat& outputImage){
outputImage = inputImage.clone();
int rows = outputImage.rows;
int cols = outputImage.rows;
for (int i = 0; i < rows; i++){
for (int j = 0; j < cols; j++){
Vec3b & tmp = outputImage.at(i, j);
for (int k = 0; k < 3; k++){
if (tmp[k] < 48)
tmp[k] = tmp[k] / 1.5;
else if (tmp[k] > 191)
tmp[k] = (tmp[k] - 192) * 0.5 + 223;
else tmp[k] = (tmp[k] - 38) * 1.33;
}
}
}
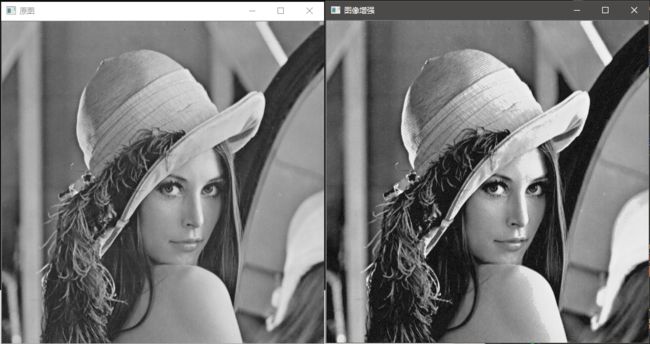
效果图:
非线性灰度变换
$$g(x,y)=clog_{10}[1+f(x,y)]$$
直方图
在数字图像处理中,直方图是最简单并且最有用的工具
灰度直方图是灰度级的函数,描述的是图像中该灰度级的像素个数
横坐标表示灰度级,纵坐标表示图像中该灰度级出现的像素个数
数据表示:
变量
含义
n
图像的像素总数
L
灰度级的个数
$r_k$
第 k 个灰度级
$n_k$
第 k 个灰度级的像素数
$p_r(r_k)$
该灰度级出现的频率
则 归一化形式:
$$p_r(r_k) = {n_k\over n},~k = 0,1,2,\cdots,L-1$$
公式利于归纳但是不利于理解,我们举个例子说明:
原始图像数据(每个位置上面的数字表示灰度级)
1
2
3
4
5
6
6
4
3
2
2
1
1
6
6
4
6
6
3
4
5
6
6
6
1
4
6
6
2
3
1
3
6
4
6
6
直方图
灰度系数
1
2
3
4
5
6
像素个数
5
4
5
6
2
14
归一化直方图数据
1/6
2/6
3/6
4/6
5/6
6/6
5/36
4/36
5/36
6/36
2/36
14/36
图像略
直方图性质
直方图未反映某一灰度级像素所在位置,即丢失了位置信息
一幅图像对应一个灰度直方图,但是不同的图像可能有相同的直方图
灰度直方图具有可加性,整幅图像的直方图等于素有不重叠子区域的直方图之和
直方图用途
反映图像的亮度、对比度、清晰度。用来判断一幅图像是否合理地利用了全部被允许的灰度级范围
图像分割阈值选取,如果某图像的灰度直方图具有二峰性,那么这个图像的较亮区域与较暗区域可以较好分离,取谷底做为阈值点
直方图计算
先求出图像灰度级总数,然后遍历图像,对应像素点的灰度级的像素个数++,最后归一化即可
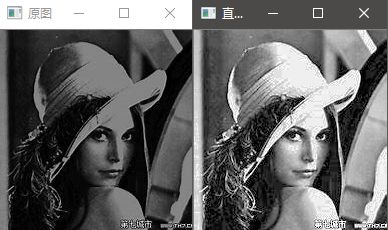
直方图均衡化
目的:将$p_r(k_r)$ 修正为均匀分布形式,使动态范围增加,图像清晰度增加,对比度增加
方法:
求出灰度直方图
计算累积分布$p's(s_k) = \sum{j=0}^kp_r(r_j)$
计算新的灰度值$s_k=int[(L-1)p's(s_k)+0.5]$
$r_k$
$n_k$
$p_r(r_k)$
$p'_s(s_k)$
$s_k$
$N'_k$
$p_s(s_k)$
0
790
0.19
0.19
1
0
0
1
1023
0.25
0.44
3
790
0.19
2
850
0.21
0.65
5
0
0
3
656
0.16
0.81
6
1023
0.25
4
329
0.08
0.89
6
0
0
5
245
0.06
0.95
7
850
0.21
6
122
0.03
0.98
7
985
0.24
7
81
0.02
1.00
7
488
0.11
新的 $N'_k$ 由上一级的$n_k$ 而来
//可以直接调用opencv库写好的方法
void equalization(Mat &input, Mat &output){
Mat imageRGB[3];
split(input, imageRGB);
for (int i = 0; i < 3;i++)
equalizeHist(imageRGB[i], imageRGB[i]);
merge(imageRGB, 3, output);
}