onnx标准 & onnxRuntime加速推理引擎
onnx标准 & onnxRuntime加速推理引擎
文章目录
- onnx标准 & onnxRuntime加速推理引擎
-
- 一、onnx简介
- 二、pytorch转onnx
- 三、tf1.0 / tf2.0 ckpt转onnx
- 四、python onnx的使用
-
- 1、环境安装
-
- 1)CPU版本
- 2)GPU版本
- 3)存在的问题1
- 4)存在的问题2
- 2、获得onnx模型权重参数(可视化)
- 3、onnx模型推理
- 五、onnx推理效率:和Module & DataParallel比较
参考博客:
- ONNX运行时:跨平台、高性能ML推断和训练加速器
- python关于onnx模型的一些基本操作
- ONNX 與 Azure Machine Learning:建立並加速 ML 模型
- 超有用ONNX参考资料整理
- 模型部署之 ONNX ONNXRuntime
参考官方文档:
- onnx training-start
- Get started with ORT for Python
- onnxruntime API
- MPI: Parallel Programming in Python with Message Passing Interface (mpi4py)
- onnx使用介绍 (PPT)
一、onnx简介
通常我们在训练模型时可以使用很多不同的框架,比如有的同学喜欢用 Pytorch,有的同学喜欢使用 TensorFLow,也有的喜欢 MXNet,以及深度学习最开始流行的 Caffe等等,这样不同的训练框架就导致了产生不同的模型结果包,在模型进行部署推理时就需要不同的依赖库,而且同一个框架比如tensorflow 不同的版本之间的差异较大, 为了解决这个混乱问题,LF AI 这个组织联合 Facebook, MicroSoft等公司制定了机器学习模型的标准,这个标准叫做ONNX, Open Neural Network Exchage,所有其他框架产生的模型包 (.pth, .pb) 都可以转换成这个标准格式,转换成这个标准格式后,就可以使用统一的 ONNX Runtime等工具进行统一部署。(和Java生成的中间文件可以在JVM上运行一样,onnx runtime引擎为生成的onnx模型文件提供推理功能)
onnx主页: onnxruntime.ai
开发文档和教程: onnxruntime.ai/docs
Companion sample repositories:
- 基于ONNX Runtime 的推理: microsoft/onnxruntime-inference-examples
- 基于ONNX Runtime 的训练: microsoft/onnxruntime-training-examples
onnx支持的算子:https://github.com/onnx/onnx/blob/main/docs/Operators.md
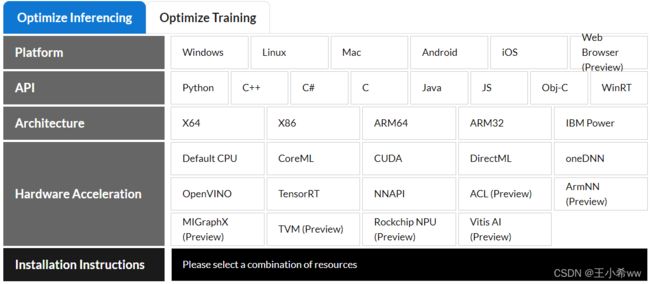
onnx支持哪些平台、为哪些语言提供了API、支持的指令集架构、支持哪些硬件的加速:
Note:
onnx为机器学习模型定义了一个标准,和TensorFlow,Caffe都属于主流的模型格式,并且提供了onnx runtime并行加速推理包,包括对ONNX 模型进行解读,优化(融合conv-bn等操作),运行,方便AI模型的移植和部署。在使用SCRFD发现,原生的
onnx runtime加载onnx模型并完成推理的确比cv2.dnn.readNet(onnx)的效率高得多,差不多是后者的一倍多,该博主也给出相同的结论:https://blog.csdn.net/woshicver/article/details/113764970。onnx也为主流的机器学习框架提供模型训练,这里主要是pytorch,官网说会比之前在pytorch训练快上1.4倍。只需要在加载模型时修改成:
from torch_ort import ORTModule model = ORTModule(model)有兴趣的参考microsoft/onnxruntime-training-examples,https://cloudblogs.microsoft.com/opensource/2021/07/13/accelerate-pytorch-training-with-torch-ort/
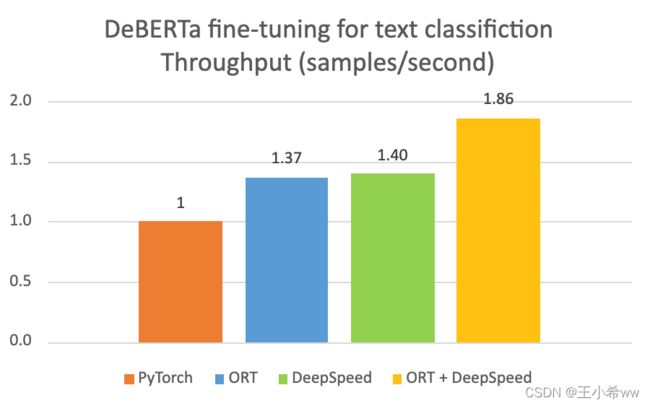
其实除了onnx提供了onnxRuntime推理引擎,还有比如阿里的**MNN轻量级高性能推理引擎,腾讯的NCNN,Nvidia的TensorRT**等
参考主流的深度学习推理架构有哪些呢?
ONNX源码阅读
- onnxruntime源码解析:引擎运行过程总览
- pytorch-onnx-operator-export-type设置
- onnxruntime与pytorch对接方法汇总
- onnxruntime的设计理念
二、pytorch转onnx
参考
- (OPTIONAL) EXPORTING A MODEL FROM PYTORCH TO ONNX AND RUNNING IT USING ONNX RUNTIME
- 将 PyTorch 模型转换为 ONNX
在模型的推理阶段中,通过传入模型和输入的Tensor,利用torch.onnx即可实现pth文件到onnx文件的转化
#Function to Convert to ONNX
def Convert_ONNX(model,input):
# set the model to inference mode
model.eval()
# Let's create a dummy input tensor
dummy_input = input
# Export the model
torch.onnx.export(model, # model being run
dummy_input, # model input (or a tuple for multiple inputs)
"ImageClassifier.onnx", # where to save the model
export_params=True, # store the trained parameter weights inside the model file
opset_version=13, # the ONNX version to export the model to
do_constant_folding=True, # whether to execute constant folding for optimization
input_names = ['modelInput'], # the model's input names
output_names = ['modelOutput'], # the model's output names
dynamic_axes={'modelInput' : {0 : 'batch_size'}, # variable length axes
'modelOutput' : {0 : 'batch_size'}})
print(" ")
print('Model has been converted to ONNX')
if __name__ == '__main__':
checkpoints = torch.load("./pth/mobileNetV3_SMART_CE.pth",map_location="cpu") #全部权重加载到模型中
model.load_state_dict(checkpoints)
# device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device = torch.device("cpu")
model = model.to(device)
Convert_ONNX(model, sample)
但是在使用MobileNetV3的pth文件转onnx时,存在问题:
RuntimeError: Exporting the operator relu6 to ONNX opset version 11 is not supported. Please feel free to request support or submit a pull request on PyTorch GitHub.
原因是relu6(也就是hardSigmoid)只在MobileNetV3中实现,onnx中不存在该算子,参考https://github.com/pytorch/vision/issues/3463,https://github.com/onnx/onnx/blob/main/docs/Operators.md。
解决方法:
- Native support exporting
F.hardsigmoidto onnx.- Replace
F.hardsigmoidwithF.hardtanhthat is friendly for exporting and equal numerically as I did above.class hswish(nn.Module): def forward(self, x): out = x * F.hardtanh(x + 3, inplace=True) / 6 return out class hsigmoid(nn.Module): def forward(self, x): out = F.hardtanh(x + 3, inplace=True) / 6 return out
三、tf1.0 / tf2.0 ckpt转onnx
参考将tensorflow 1.x & 2.x转化成onnx文件
四、python onnx的使用
- Get started with ORT for Python
- onnxruntime API
1、环境安装
If using pip, run pip install --upgrade pip prior to downloading.
| Artifact | Description | Supported Platforms |
|---|---|---|
| onnxruntime | CPU (Release 稳定版) | Windows (x64), Linux (x64, ARM64), Mac (X64), |
| ort-nightly | CPU (Dev 测试版) | Same as above |
| onnxruntime-gpu | GPU (Release) | Windows (x64), Linux (x64, ARM64) |
| ort-nightly-gpu | GPU (Dev) | Same as above |
pip命令如下:
pip install onnxruntime
1)CPU版本
self.ort_sess = onnxruntime.InferenceSession(rootPath + landmark_model_path) # Create inference session using ort.InferenceSession
2)GPU版本
-
和cpu一样,导入onnxruntime包即可,无需加上’-gpu’;
-
只需加个provider即可,参考onnx 需要指定provider
self.ort_sess = onnxruntime.InferenceSession(rootPath + landmark_model_path,providers=['CUDAExecutionProvider']) # Create inference session using ort.InferenceSession
3)存在的问题1
安装的onnxruntime-gpu和cuda不匹配
RuntimeError: D:\a\_work\1\s\onnxruntime\python\onnxruntime_pybind_state.cc:531 onnxruntime::python::CreateExecutionProviderInstance CUDA_PATH is set but CUDA wasn't able to be loaded. Please install the correct version of CUDA and cuDNN as mentioned in the GPU requirements page (https://onnxruntime.ai/docs/reference/execution-providers/CUDA-ExecutionProvider.html#requirements), make sure they're in the PATH, and that your GPU is supported.
解决方法:参考 https://onnxruntime.ai/docs/execution-providers/CUDA-ExecutionProvider.html
-
查看CUDA:
nvcc --version nvcc: NVIDIA (R) Cuda compiler driver Copyright (c) 2005-2018 NVIDIA Corporation Built on Sat_Aug_25_21:08:04_Central_Daylight_Time_2018 Cuda compilation tools, release 10.0, V10.0.130 -
查看cuDNN:参考Linux 和 Windows 查看 CUDA 和 cuDNN 版本
# 使用 PyTorch 查看 CUDA 和 cuDNN 版本 import torch print(torch.__version__) print(torch.version.cuda) print(torch.backends.cudnn.version()) --- 1.9.0+cu102 10.2 7605 -
对照下面表格:安装
onnxruntime-gpu==1.2ONNX Runtime CUDA cuDNN Notes 1.10 11.4 8.2.4 (Linux) 8.2.2.26 (Windows) libcudart 11.4.43 libcufft 10.5.2.100 libcurand 10.2.5.120 libcublasLt 11.6.1.51 libcublas 11.6.1.51 libcudnn 8.2.4 1.9 11.4 8.2.4 (Linux) 8.2.2.26 (Windows) libcudart 11.4.43 libcufft 10.5.2.100 libcurand 10.2.5.120 libcublasLt 11.6.1.51 libcublas 11.6.1.51 libcudnn 8.2.4 1.8 11.0.3 8.0.4 (Linux) 8.0.2.39 (Windows) libcudart 11.0.221 libcufft 10.2.1.245 libcurand 10.2.1.245 libcublasLt 11.2.0.252 libcublas 11.2.0.252 libcudnn 8.0.4 1.7 11.0.3 8.0.4 (Linux) 8.0.2.39 (Windows) libcudart 11.0.221 libcufft 10.2.1.245 libcurand 10.2.1.245 libcublasLt 11.2.0.252 libcublas 11.2.0.252 libcudnn 8.0.4 1.5-1.6 10.2 8.0.3 CUDA 11 can be built from source 1.2-1.4 10.1 7.6.5 Requires cublas10-10.2.1.243; cublas 10.1.x will not work 1.0-1.1 10.0 7.6.4 CUDA versions from 9.1 up to 10.1, and cuDNN versions from 7.1 up to 7.4 should also work with Visual Studio 2017 -
由于我的CUDA是10.0,所以onnxruntime也要降至1.2版本(如果不行,安装
onnxruntime-gpu == 1.1),否则会报错from onnxruntime.capi._pybind_state import get_all_providers, get_available_providers, get_device, set_seed, RunOptions, SessionOptions, set_default_logger_severity, NodeArg, ModelMetadata, GraphOptimizationLevel, ExecutionMode, OrtDevice, SessionIOBinding ImportError: cannot import name 'get_all_providers'会发现
onnxruntime和onnxruntime-gpu版本是一致的:onnxruntime, onnxruntime-gpu
而且还要注意一点:
需要先安装onnxruntime,再安装onnxruntime-gpu,这样才能使用GPU,否则下面
print(onnxruntime.get_device()) #检测当前的硬件情况 self.ort_sess = onnxruntime.InferenceSession(rootPath + landmark_model_path,providers=['CUDAExecutionProvider']) # Create inference session using ort.InferenceSessionprint(onnxruntime.get_device())一直输出CPU
4)存在的问题2
打包的onnx文件不适用于该版本的onnxruntime,需要重新打包
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : This is an invalid model. Error in Node:Conv_0 : No Op registered for Conv with domain_version of 13
参考https://blog.csdn.net/qq_279033270/article/details/109583514
重新将pth文件转换成onnx
'''pth转onnx'''
# Export the model
torch.onnx.export(landmark_detector, # model being run
input, # model input (or a tuple for multiple inputs)
"ImageClassifier.onnx", # where to save the model
export_params=True, # store the trained parameter weights inside the model file
opset_version=9, # the ONNX version to export the model to
do_constant_folding=True, # whether to execute constant folding for optimization
input_names=['modelInput'], # the model's input names
output_names=['modelOutput'], # the model's output names
dynamic_axes={'modelInput': {0: 'batch_size'}, # variable length axes
'modelOutput': {0: 'batch_size'}})
print(" ")
print('Model has been converted to ONNX')
2、获得onnx模型权重参数(可视化)
-
https://netron.app/
-
模型部署之 ONNX ONNXRuntime
这里以SCRFD模型为例
import cv2
import onnx
from onnx import helper
import onnxruntime
import numpy as np
'''一、获取onnx模型的输出层,输出层和模型中的节点数'''
if __name__ == '__main__':
# 参考 , https://onnxruntime.ai/docs/get-started/with-python.html
# 加载模型
# model = onnx.load('./weights/mbv2_ID_recognition.onnx') # Load the onnx model with onnx.load
model = onnx.load('./weights/scrfd_500m_kps.onnx')
# model = onnx.load('./weights/mbv3_fire_classifier.onnx')
# 检查模型格式是否完整及正确
onnx.checker.check_model(model)
'''
ref: https://github.com/onnx/onnx/blob/main/docs/IR.md
Graphs have the following properties:
name: string The name of the model graph.
node: Node[] A list of nodes, forming a partially ordered computation graph based on input/output data dependencies. It is in topological order.
initializer: Tensor[] A list of named tensor values. When an initializer has the same name as a graph input, it specifies a default value for that input. When an initializer has a name different from all graph inputs, it specifies a constant value. The order of the list is unspecified.
doc_string: string Human-readable documentation for this model. Markdown is allowed.
input: ValueInfo[] The input parameters of the graph, possibly initialized by a default value found in ‘initializer.’
output: ValueInfo[] The output parameters of the graph. Once all output parameters have been written to by a graph execution, the execution is complete.
value_info: ValueInfo[] Used to store the type and shape information of values that are not inputs or outputs.
'''
input = model.graph.input # 获取输入层,包含层名称、维度信息
output = model.graph.output # 获取输出层,包含层名称、维度信息
depth = len(model.graph.node) # 获取节点数
doc_string = model.graph.doc_string # 获取关于onnx模型的相关文档,是在哪里转换的
print(f"input = {input}")
print(f"output = {output}")
print(f"depth = {depth}")
print(f"doc_string = {doc_string}")
# 参考 https://www.jianshu.com/p/476478c17b8e
# Print a human readable representation of the graph
print(onnx.helper.printable_graph(model.graph))
输出结果:
input = [name: "images"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 3
}
dim {
dim_value: 640
}
dim {
dim_value: 640
}
}
}
}
]
output = [name: "out0"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 12800
}
dim {
dim_value: 1
}
}
}
}
, name: "out1"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 3200
}
dim {
dim_value: 1
}
}
}
}
, name: "out2"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 800
}
dim {
dim_value: 1
}
}
}
}
, name: "out3"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 12800
}
dim {
dim_value: 4
}
}
}
}
, name: "out4"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 3200
}
dim {
dim_value: 4
}
}
}
}
, name: "out5"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 800
}
dim {
dim_value: 4
}
}
}
}
, name: "out6"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 12800
}
dim {
dim_value: 10
}
}
}
}
, name: "out7"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 3200
}
dim {
dim_value: 10
}
}
}
}
, name: "out8"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 1
}
dim {
dim_value: 800
}
dim {
dim_value: 10
}
}
}
}
]
depth = 191
doc_string =
graph torch-jit-export (
%images[FLOAT, 1x3x640x640]
) initializers (
%neck.lateral_convs.0.conv.weight[FLOAT, 16x72x1x1]
%neck.lateral_convs.0.conv.bias[FLOAT, 16]
%neck.lateral_convs.1.conv.weight[FLOAT, 16x152x1x1]
%neck.lateral_convs.1.conv.bias[FLOAT, 16]
%neck.lateral_convs.2.conv.weight[FLOAT, 16x288x1x1]
%neck.lateral_convs.2.conv.bias[FLOAT, 16]
%neck.fpn_convs.0.conv.weight[FLOAT, 16x16x3x3]
%neck.fpn_convs.0.conv.bias[FLOAT, 16]
%neck.fpn_convs.1.conv.weight[FLOAT, 16x16x3x3]
%neck.fpn_convs.1.conv.bias[FLOAT, 16]
%neck.fpn_convs.2.conv.weight[FLOAT, 16x16x3x3]
%neck.fpn_convs.2.conv.bias[FLOAT, 16]
%neck.downsample_convs.0.conv.weight[FLOAT, 16x16x3x3]
%neck.downsample_convs.0.conv.bias[FLOAT, 16]
%neck.downsample_convs.1.conv.weight[FLOAT, 16x16x3x3]
%neck.downsample_convs.1.conv.bias[FLOAT, 16]
%neck.pafpn_convs.0.conv.weight[FLOAT, 16x16x3x3]
%neck.pafpn_convs.0.conv.bias[FLOAT, 16]
%neck.pafpn_convs.1.conv.weight[FLOAT, 16x16x3x3]
%neck.pafpn_convs.1.conv.bias[FLOAT, 16]
%bbox_head.stride_cls.(8, 8).weight[FLOAT, 2x64x3x3]
%bbox_head.stride_cls.(8, 8).bias[FLOAT, 2]
%bbox_head.stride_cls.(16, 16).weight[FLOAT, 2x64x3x3]
%bbox_head.stride_cls.(16, 16).bias[FLOAT, 2]
%bbox_head.stride_cls.(32, 32).weight[FLOAT, 2x64x3x3]
%bbox_head.stride_cls.(32, 32).bias[FLOAT, 2]
%bbox_head.stride_reg.(8, 8).weight[FLOAT, 8x64x3x3]
%bbox_head.stride_reg.(8, 8).bias[FLOAT, 8]
%bbox_head.stride_reg.(16, 16).weight[FLOAT, 8x64x3x3]
%bbox_head.stride_reg.(16, 16).bias[FLOAT, 8]
%bbox_head.stride_reg.(32, 32).weight[FLOAT, 8x64x3x3]
%bbox_head.stride_reg.(32, 32).bias[FLOAT, 8]
%bbox_head.stride_kps.(8, 8).weight[FLOAT, 20x64x3x3]
%bbox_head.stride_kps.(8, 8).bias[FLOAT, 20]
%bbox_head.stride_kps.(16, 16).weight[FLOAT, 20x64x3x3]
%bbox_head.stride_kps.(16, 16).bias[FLOAT, 20]
%bbox_head.stride_kps.(32, 32).weight[FLOAT, 20x64x3x3]
%bbox_head.stride_kps.(32, 32).bias[FLOAT, 20]
%555[FLOAT, 16x3x3x3]
%556[FLOAT, 16]
%558[FLOAT, 16x1x3x3]
%559[FLOAT, 16]
%561[FLOAT, 16x16x1x1]
%562[FLOAT, 16]
%564[FLOAT, 16x1x3x3]
%565[FLOAT, 16]
%567[FLOAT, 40x16x1x1]
%568[FLOAT, 40]
%570[FLOAT, 40x1x3x3]
%571[FLOAT, 40]
%573[FLOAT, 40x40x1x1]
%574[FLOAT, 40]
%576[FLOAT, 40x1x3x3]
%577[FLOAT, 40]
%579[FLOAT, 72x40x1x1]
%580[FLOAT, 72]
%582[FLOAT, 72x1x3x3]
%583[FLOAT, 72]
%585[FLOAT, 72x72x1x1]
%586[FLOAT, 72]
%588[FLOAT, 72x1x3x3]
%589[FLOAT, 72]
%591[FLOAT, 72x72x1x1]
%592[FLOAT, 72]
%594[FLOAT, 72x1x3x3]
%595[FLOAT, 72]
%597[FLOAT, 152x72x1x1]
%598[FLOAT, 152]
%600[FLOAT, 152x1x3x3]
%601[FLOAT, 152]
%603[FLOAT, 152x152x1x1]
%604[FLOAT, 152]
%606[FLOAT, 152x1x3x3]
%607[FLOAT, 152]
%609[FLOAT, 288x152x1x1]
%610[FLOAT, 288]
%612[FLOAT, 288x1x3x3]
%613[FLOAT, 288]
%615[FLOAT, 288x288x1x1]
%616[FLOAT, 288]
%618[FLOAT, 288x1x3x3]
%619[FLOAT, 288]
%621[FLOAT, 288x288x1x1]
%622[FLOAT, 288]
%624[FLOAT, 288x1x3x3]
%625[FLOAT, 288]
%627[FLOAT, 288x288x1x1]
%628[FLOAT, 288]
%630[FLOAT, 288x1x3x3]
%631[FLOAT, 288]
%633[FLOAT, 288x288x1x1]
%634[FLOAT, 288]
%636[FLOAT, 288x1x3x3]
%637[FLOAT, 288]
%639[FLOAT, 288x288x1x1]
%640[FLOAT, 288]
%642[FLOAT, 16x1x3x3]
%643[FLOAT, 16]
%645[FLOAT, 64x16x1x1]
%646[FLOAT, 64]
%648[FLOAT, 64x1x3x3]
%649[FLOAT, 64]
%651[FLOAT, 64x64x1x1]
%652[FLOAT, 64]
%654[FLOAT, 16x1x3x3]
%655[FLOAT, 16]
%657[FLOAT, 64x16x1x1]
%658[FLOAT, 64]
%660[FLOAT, 64x1x3x3]
%661[FLOAT, 64]
%663[FLOAT, 64x64x1x1]
%664[FLOAT, 64]
%666[FLOAT, 16x1x3x3]
%667[FLOAT, 16]
%669[FLOAT, 64x16x1x1]
%670[FLOAT, 64]
%672[FLOAT, 64x1x3x3]
%673[FLOAT, 64]
%675[FLOAT, 64x64x1x1]
%676[FLOAT, 64]
%677[INT64, 1]
%678[INT64, 1]
%679[INT64, 1]
%680[INT64, 1]
%681[INT64, 1]
%682[INT64, 1]
%683[INT64, 1]
%684[INT64, 1]
%685[INT64, 1]
%686[INT64, 1]
%687[INT64, 1]
%688[INT64, 1]
%689[INT64, 1]
%690[INT64, 1]
%691[INT64, 1]
%692[INT64, 1]
%693[INT64, 1]
%694[INT64, 1]
) {
%554 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%images, %555, %556)
%288 = Relu(%554)
%557 = Conv[dilations = [1, 1], group = 16, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%288, %558, %559)
%291 = Relu(%557)
%560 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%291, %561, %562)
%294 = Relu(%560)
%563 = Conv[dilations = [1, 1], group = 16, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%294, %564, %565)
%297 = Relu(%563)
%566 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%297, %567, %568)
%300 = Relu(%566)
%569 = Conv[dilations = [1, 1], group = 40, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%300, %570, %571)
%303 = Relu(%569)
%572 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%303, %573, %574)
%306 = Relu(%572)
%575 = Conv[dilations = [1, 1], group = 40, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%306, %576, %577)
%309 = Relu(%575)
%578 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%309, %579, %580)
%312 = Relu(%578)
%581 = Conv[dilations = [1, 1], group = 72, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%312, %582, %583)
%315 = Relu(%581)
%584 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%315, %585, %586)
%318 = Relu(%584)
%587 = Conv[dilations = [1, 1], group = 72, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%318, %588, %589)
%321 = Relu(%587)
%590 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%321, %591, %592)
%324 = Relu(%590)
%593 = Conv[dilations = [1, 1], group = 72, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%324, %594, %595)
%327 = Relu(%593)
%596 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%327, %597, %598)
%330 = Relu(%596)
%599 = Conv[dilations = [1, 1], group = 152, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%330, %600, %601)
%333 = Relu(%599)
%602 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%333, %603, %604)
%336 = Relu(%602)
%605 = Conv[dilations = [1, 1], group = 152, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%336, %606, %607)
%339 = Relu(%605)
%608 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%339, %609, %610)
%342 = Relu(%608)
%611 = Conv[dilations = [1, 1], group = 288, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%342, %612, %613)
%345 = Relu(%611)
%614 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%345, %615, %616)
%348 = Relu(%614)
%617 = Conv[dilations = [1, 1], group = 288, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%348, %618, %619)
%351 = Relu(%617)
%620 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%351, %621, %622)
%354 = Relu(%620)
%623 = Conv[dilations = [1, 1], group = 288, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%354, %624, %625)
%357 = Relu(%623)
%626 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%357, %627, %628)
%360 = Relu(%626)
%629 = Conv[dilations = [1, 1], group = 288, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%360, %630, %631)
%363 = Relu(%629)
%632 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%363, %633, %634)
%366 = Relu(%632)
%635 = Conv[dilations = [1, 1], group = 288, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%366, %636, %637)
%369 = Relu(%635)
%638 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%369, %639, %640)
%372 = Relu(%638)
%373 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%324, %neck.lateral_convs.0.conv.weight, %neck.lateral_convs.0.conv.bias)
%374 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%336, %neck.lateral_convs.1.conv.weight, %neck.lateral_convs.1.conv.bias)
%375 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%372, %neck.lateral_convs.2.conv.weight, %neck.lateral_convs.2.conv.bias)
%376 = Shape(%374)
%377 = Constant[value = <Scalar Tensor []>]()
%378 = Gather[axis = 0](%376, %377)
%379 = Shape(%374)
%380 = Constant[value = <Scalar Tensor []>]()
%381 = Gather[axis = 0](%379, %380)
%382 = Unsqueeze[axes = [0]](%378)
%383 = Unsqueeze[axes = [0]](%381)
%384 = Concat[axis = 0](%382, %383)
%385 = Shape(%375)
%386 = Constant[value = <Tensor>]()
%387 = Constant[value = <Tensor>]()
%388 = Constant[value = <Tensor>]()
%389 = Slice(%385, %387, %388, %386)
%390 = Cast[to = 7](%384)
%391 = Concat[axis = 0](%389, %390)
%392 = Constant[value = <Tensor>]()
%393 = Constant[value = <Tensor>]()
%394 = Resize[coordinate_transformation_mode = 'asymmetric', cubic_coeff_a = -0.75, mode = 'nearest', nearest_mode = 'floor'](%375, %392, %393, %391)
%395 = Add(%374, %394)
%396 = Shape(%373)
%397 = Constant[value = <Scalar Tensor []>]()
%398 = Gather[axis = 0](%396, %397)
%399 = Shape(%373)
%400 = Constant[value = <Scalar Tensor []>]()
%401 = Gather[axis = 0](%399, %400)
%402 = Unsqueeze[axes = [0]](%398)
%403 = Unsqueeze[axes = [0]](%401)
%404 = Concat[axis = 0](%402, %403)
%405 = Shape(%395)
%406 = Constant[value = <Tensor>]()
%407 = Constant[value = <Tensor>]()
%408 = Constant[value = <Tensor>]()
%409 = Slice(%405, %407, %408, %406)
%410 = Cast[to = 7](%404)
%411 = Concat[axis = 0](%409, %410)
%412 = Constant[value = <Tensor>]()
%413 = Constant[value = <Tensor>]()
%414 = Resize[coordinate_transformation_mode = 'asymmetric', cubic_coeff_a = -0.75, mode = 'nearest', nearest_mode = 'floor'](%395, %412, %413, %411)
%415 = Add(%373, %414)
%416 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%415, %neck.fpn_convs.0.conv.weight, %neck.fpn_convs.0.conv.bias)
%417 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%395, %neck.fpn_convs.1.conv.weight, %neck.fpn_convs.1.conv.bias)
%418 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%375, %neck.fpn_convs.2.conv.weight, %neck.fpn_convs.2.conv.bias)
%419 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%416, %neck.downsample_convs.0.conv.weight, %neck.downsample_convs.0.conv.bias)
%420 = Add(%417, %419)
%421 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [2, 2]](%420, %neck.downsample_convs.1.conv.weight, %neck.downsample_convs.1.conv.bias)
%422 = Add(%418, %421)
%423 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%420, %neck.pafpn_convs.0.conv.weight, %neck.pafpn_convs.0.conv.bias)
%424 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%422, %neck.pafpn_convs.1.conv.weight, %neck.pafpn_convs.1.conv.bias)
%641 = Conv[dilations = [1, 1], group = 16, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%416, %642, %643)
%427 = Relu(%641)
%644 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%427, %645, %646)
%430 = Relu(%644)
%647 = Conv[dilations = [1, 1], group = 64, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%430, %648, %649)
%433 = Relu(%647)
%650 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%433, %651, %652)
%436 = Relu(%650)
%437 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%436, %bbox_head.stride_cls.(8, 8).weight, %bbox_head.stride_cls.(8, 8).bias)
%438 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%436, %bbox_head.stride_reg.(8, 8).weight, %bbox_head.stride_reg.(8, 8).bias)
%439 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%436, %bbox_head.stride_kps.(8, 8).weight, %bbox_head.stride_kps.(8, 8).bias)
%440 = Shape(%437)
%441 = Constant[value = <Scalar Tensor []>]()
%442 = Gather[axis = 0](%440, %441)
%443 = Transpose[perm = [0, 2, 3, 1]](%437)
%446 = Unsqueeze[axes = [0]](%442)
%449 = Concat[axis = 0](%446, %677, %678)
%450 = Reshape(%443, %449)
%out0 = Sigmoid(%450)
%452 = Transpose[perm = [0, 2, 3, 1]](%438)
%455 = Unsqueeze[axes = [0]](%442)
%458 = Concat[axis = 0](%455, %679, %680)
%out3 = Reshape(%452, %458)
%460 = Transpose[perm = [0, 2, 3, 1]](%439)
%463 = Unsqueeze[axes = [0]](%442)
%466 = Concat[axis = 0](%463, %681, %682)
%out6 = Reshape(%460, %466)
%653 = Conv[dilations = [1, 1], group = 16, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%423, %654, %655)
%470 = Relu(%653)
%656 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%470, %657, %658)
%473 = Relu(%656)
%659 = Conv[dilations = [1, 1], group = 64, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%473, %660, %661)
%476 = Relu(%659)
%662 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%476, %663, %664)
%479 = Relu(%662)
%480 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%479, %bbox_head.stride_cls.(16, 16).weight, %bbox_head.stride_cls.(16, 16).bias)
%481 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%479, %bbox_head.stride_reg.(16, 16).weight, %bbox_head.stride_reg.(16, 16).bias)
%482 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%479, %bbox_head.stride_kps.(16, 16).weight, %bbox_head.stride_kps.(16, 16).bias)
%483 = Shape(%480)
%484 = Constant[value = <Scalar Tensor []>]()
%485 = Gather[axis = 0](%483, %484)
%486 = Transpose[perm = [0, 2, 3, 1]](%480)
%489 = Unsqueeze[axes = [0]](%485)
%492 = Concat[axis = 0](%489, %683, %684)
%493 = Reshape(%486, %492)
%out1 = Sigmoid(%493)
%495 = Transpose[perm = [0, 2, 3, 1]](%481)
%498 = Unsqueeze[axes = [0]](%485)
%501 = Concat[axis = 0](%498, %685, %686)
%out4 = Reshape(%495, %501)
%503 = Transpose[perm = [0, 2, 3, 1]](%482)
%506 = Unsqueeze[axes = [0]](%485)
%509 = Concat[axis = 0](%506, %687, %688)
%out7 = Reshape(%503, %509)
%665 = Conv[dilations = [1, 1], group = 16, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%424, %666, %667)
%513 = Relu(%665)
%668 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%513, %669, %670)
%516 = Relu(%668)
%671 = Conv[dilations = [1, 1], group = 64, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%516, %672, %673)
%519 = Relu(%671)
%674 = Conv[dilations = [1, 1], group = 1, kernel_shape = [1, 1], pads = [0, 0, 0, 0], strides = [1, 1]](%519, %675, %676)
%522 = Relu(%674)
%523 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%522, %bbox_head.stride_cls.(32, 32).weight, %bbox_head.stride_cls.(32, 32).bias)
%524 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%522, %bbox_head.stride_reg.(32, 32).weight, %bbox_head.stride_reg.(32, 32).bias)
%525 = Conv[dilations = [1, 1], group = 1, kernel_shape = [3, 3], pads = [1, 1, 1, 1], strides = [1, 1]](%522, %bbox_head.stride_kps.(32, 32).weight, %bbox_head.stride_kps.(32, 32).bias)
%526 = Shape(%523)
%527 = Constant[value = <Scalar Tensor []>]()
%528 = Gather[axis = 0](%526, %527)
%529 = Transpose[perm = [0, 2, 3, 1]](%523)
%532 = Unsqueeze[axes = [0]](%528)
%535 = Concat[axis = 0](%532, %689, %690)
%536 = Reshape(%529, %535)
%out2 = Sigmoid(%536)
%538 = Transpose[perm = [0, 2, 3, 1]](%524)
%541 = Unsqueeze[axes = [0]](%528)
%544 = Concat[axis = 0](%541, %691, %692)
%out5 = Reshape(%538, %544)
%546 = Transpose[perm = [0, 2, 3, 1]](%525)
%549 = Unsqueeze[axes = [0]](%528)
%552 = Concat[axis = 0](%549, %693, %694)
%out8 = Reshape(%546, %552)
return %out0, %out1, %out2, %out3, %out4, %out5, %out6, %out7, %out8
}
可以看到其输出有3个dict,一个是 input, 一个是 initializers,以及最后一个是operators把输入和权重 initialization 进行类似于 forward操作,在最后一个dict operators中其返回是 %191,也就是 gemm 最后一个全连接的输出。
利用netron在线工具https://netron.app/ 查看SCRFD模型结构(SCRFD中FPN每一层对应3个head)
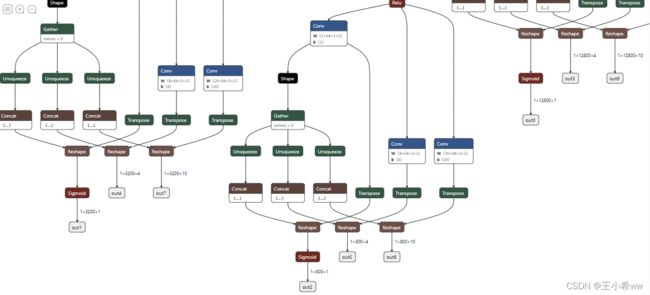
3、onnx模型推理
这里使用SCRFD模型进行推理
import cv2
import onnx
from onnx import helper
import onnxruntime
import numpy as np
'''三、onnx模型推理'''
if __name__ == '__main__':
ort_sess = onnxruntime.InferenceSession('./weights/scrfd_500m_kps.onnx') # Create inference session using ort.InferenceSession
# 加载图片
img = cv2.imread("./img/calibrate_glasses.jpg")
img = cv2.resize(img, (640, 640))
img = img.astype(np.float32) / 255.
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img = img.reshape((3,640,640))
if len(img.shape) == 3:
img = np.expand_dims(img, 0)
outputs = ort_sess.run(None, {'images': img}) # 调用实例sess的run方法进行推理
print(f"length of outputs = {len(outputs)}")
---
length of outputs = 9
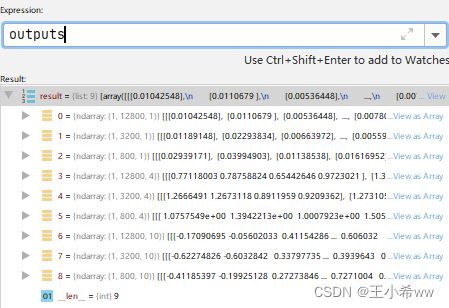
模型的输出结果和上面的可视化的模型结果是一致的,FPN有3层,每层FPN有3个head,共9个输出。
五、onnx推理效率:和Module & DataParallel比较
跳转至onnx效率问题:和Module & DataParallel比较