算法：Trie字典（前缀）树

什么是“Trie树”

Trie 树，也叫“字典树”。顾名思义，它是一个树形结构。是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题、

当然，这样一个问题可以有多种解决方法，比如散列表、红黑树，Trie树等。

那Trie树到底长什么样子呢？

• 举个例子，我们有6个字符串，它们分别是：how、hi、her、hello、so、see。我们希望在里面多次查找某个字符串是否存在。如果每次查找，都是拿要查找的字符串跟这6个字符串依次进行字符串匹配，那效率就比较低，有没有更高效的方法呢？
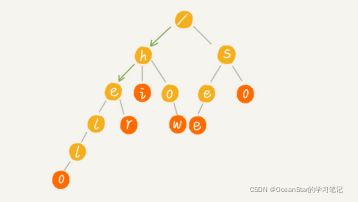
• 这个时候，我们就可以先对这6个字符串做一下预处理，组织成Trie树的结构，之后，每次查找，都是在Trie树中进行匹配查找。Trie树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。最后构造出来的就是下面这样图中的样子。

• 其中：
  • 根节点不包含字符，除根节点以外每个节点只包含一个字符
  • 从根节点到红色节点的一条路径，路径上经过的字符连接起来，为该节点对应的字符串（注意，红色节点不是叶子节点）
  • 每个节点的所有子节点包含的字符串不相同。

其具体构建过程如下图。

• 构造过程的每一步，都相当于往Trie树中插入一个字符串。当所有字符串都插入完成之后，Tire树就构建好了。

• 当我们在Tire树中查找一个字符串的时候，比如查找字符串“her”，那我们将要查找的字符串分隔成单个的字符h、e、r，然后从Trie树的根节点开始匹配。如下图，绿色的路径就是在Trie树中匹配的路径。

• 如果我们将要查找的字符串是“he”呢？我们还是上面同样的方法，从根节点开始，沿着某条路径来匹配，如下图，绿色的路径，是字符串“he”匹配的路径。但是，路径的最后一个节点“e”并不是红色的。也就是说，“he”是某个字符串的前缀子串，但并不能完全匹配任何字符串。

如何实现一棵 Trie 树？

• AC平台：208. 实现 Trie (前缀树)

java实现

Trie树主要有两个操作：

• 一个是将字符串集合构造成Trie树。也就是一个将字符串插入到Tire树的过程
• 一个是在Trie树中查找一个字符串

那应该如何存储一个Trie树呢？

• 从上面图中，我们可以看出，Trie树是一个多叉树。那对于多叉树来说，我们怎么存储一个节点的所有子节点的指针呢？
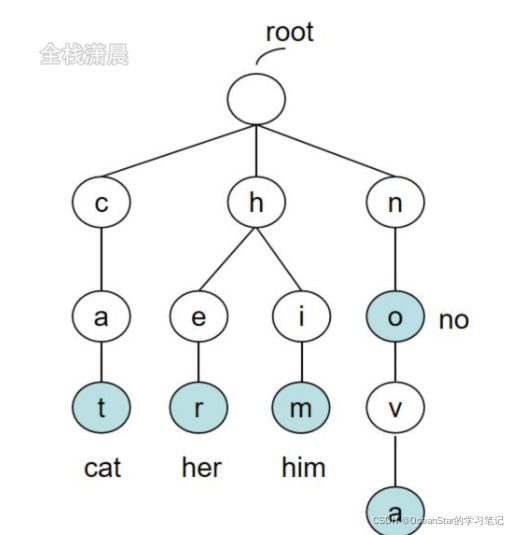
• 一种比较经典的方法是借助散列表的思想，我们通过一个下标与字符一一映射的数组，来存储子节点的指针。如下图：
  
• 假设我们的字符串只有从a到z这26个小写字母，我们在数组中下标为0的位置，存储指向子节点a的指针，下标为1的位置存储指向子节点b的指针，以此类推，下标为26的位置，存储的是指向子节点z的指针。如果某个字符的子节点不存在，我们就在对应的下标的位置存储null

  class TrieNode{
        char data;
        TrieNode children[26];
    };

• 当我们在 Trie 树中查找字符串的时候，我们就可以通过字符的 ASCII 码减去“a”的 ASCII码，迅速找到匹配的子节点的指针。比如，d 的 ASCII 码减去 a 的 ASCII 码就是 3，那子节点 d 的指针就存储在数组中下标为 3 的位置中。

java代码实现

public class TrieNode {
    public char data;
    public TrieNode []children = new TrieNode[26];
    public boolean isEndingChar = false;
    public TrieNode(char data){
        this.data = data;
    }
}


public class Trie {
    private TrieNode root = new TrieNode('/'); // 存储无意义的字符

    // 往Trie树中插入一个字符串
    public void insert(char []text){
        TrieNode p = root;
        for (int i = 0; i < text.length; i++) {
            int index = text[i] - 'a';
            if(p.children[index] == null){
                TrieNode newNode = new TrieNode(text[i]);
                p.children[index] = newNode;
            }
            p = p.children[index];
        }
        p.isEndingChar = true;
    }

    // Trie树中查找一个字符串
    public boolean find(char []pattern){
        TrieNode p = root;
        for (int i = 0; i < pattern.length; i++) {
            int index = pattern[i] - 'a';
            if(p.children[index] == null){
                return false; //不存在
            }
            p = p.children[index];
        }
        if(p.isEndingChar == false){
            return false; // 不能完全匹配，只是前缀
        }else{
            return true; //找到pattern
        }
    }
}

那么在 Trie 树中，查找某个字符串的时间复杂度是多少？

• 如果要在一组字符串中，频繁的查询某些字符串，用Trie树会非常高效。构建Trie树的过程，需要扫描所有的字符串，时间复杂度是O(n)（n表示所有字符串的长度和）。但是一旦构建成功之后，后继的查询操作会非常高效
• 每次查询时，如果要查询的字符串长度是 k，那我们只需要比对大约 k 个节点，就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说，构建好 Trie 树后，在其中查找字符串的时间复杂度是 O(k)，k 表示要查找的字符串的长度。

C++实现

实现前缀树，最常见的有数组保存（静态开辟数组），当然也可以开动态的指针类型（动态开辟内存）。至于结点对儿子的指向，一般有三种方法：

• 对每个节点开一个字母集大小的数组，对应的下标是儿子所表示的字母，内容则是这个儿子对应在大数组上的位置，即标号；
• 对每个结点挂一个链表，按一定顺序记录每个儿子是谁；
• 使用左儿子右兄弟表示法记录这棵树。

三种方法，各有特点。

• 第一种易实现，但实际的空间要求较大
• 第二种，较易实现，空间要求相对较小，但比较费时；
• 第三种，空间要求最小，但相对费时且不易写。

下面是第二种方法实现：

从二叉树说起

前缀树，也是一种树，为了理解前缀树，我们先从二叉树说起。

常见的二叉树结构是下面这样的：

class TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
}

可以看到一个数的节点中包含了三个元素：

• 该节点本身的值
• 左节点的指针
• 右节点的指针

二叉树可视化是下面这样的：

二叉树的每个节点只有两个孩子，那如果每个节点可以有多个孩子呢？这就形成了多叉树。多叉树的子节点一般不是固定的，所以会用变长数组来保存所有的子节点的指针。多叉树的结构如下：

class TreeNode {
    int val;
    vector<TreeNode*> children;
}

多叉树可视化是下面这样：

对于普通的多叉树，每个节点的所有子节点可能是没有任何规律的。而前缀树是每个节点的children 有规律的多叉树。

前缀树

（只保存小写字符的）「前缀树」是一种特殊的多叉树，字母的字典树每个节点要定义一个大小为 26 的子节点指针数组，分别对应了26个英文字符 ‘a’ ~ ‘z’，也就是说形成了一棵 26叉树。

前缀树的结构可以定义为下面这样。里面存储了两个信息：

• children 是该节点的所有子节点，字母的字典树每个节点要定义一个大小为 26 的子节点指针数组。初始化的时候讲 26 个子节点都赋为空。
• isWord 是一个标识符，用来记录到当前位置为止是否为一个词。

class TrieNode {
public:
    vector<TrieNode*> children;
    bool isWord;
    TrieNode() : isWord(false), children(26, nullptr) {
    }
    ~TrieNode() {
        for (auto& c : children)
            delete c;
    }
};

插入

在构建前缀树的时候，按照下面的方法：

• 根节点不保存任何信息
• 对于每个要插入的字符，需要算出其位置应该插入的位置，然后找是否存在这个子节点。如果不存在，则创建一个，然后再查找下一个
• 当插入结束的时候，需要把该节点的 isWord 标记为 true，说明形成了一个关键词。

下面是一棵「前缀树」，其中保存了 {“am”, “an”, “as”, “b”, “c”, “cv”} 这些关键词。图中红色表示 isWord 为 true。可以看到：

• 所有以相同字符开头的字符串，会聚合到同一个子树上。比如 {“am”, “an”, “as”} ；
• 并不一定是到达叶子节点才形成了一个关键词，只要 isWord 为true，那么从根节点到当前节点的路径就是关键词。比如 {“c”, “cv”} ；

这里并没有把字符画在了节点中。是因为前缀树是根据 字符在 children 中的位置确定子树，而不真正在树中存储了 ‘a’ ~ ‘z’ 这些字符。

查询

在判断一个关键词是否在「前缀树」中时，需要依次遍历该关键词所有字符，在前缀树中找出这条路径。可能出现三种情况：

• 在寻找路径的过程中，发现到某个位置路径断了。比如在上面的前缀树图中寻找 “d” 或者 “ar” 或者 “any” ，由于树中没有构建对应的节点，那么就查找不到这些关键词；
• 找到了这条路径，但是最后一个节点的 isWord 为 false。这也说明没有该关键词。比如在上面的前缀树图中寻找 “a” ；
• 找到了这条路径，并且最后一个节点的 isWord 为 true。这说明前缀树存储了这个关键词，比如上面前缀树图中的 “am” , “cv” 等。

实现

class TrieNode {
public:
    TrieNode () : children(26, nullptr), is_string(false){
        
    }
    ~TrieNode (){
        for(auto  it : children){
            delete it;
        }
    }

    std::vector<TrieNode  *> children;
    bool is_string;
};


class Trie {
public:
    Trie (){
        root = new TrieNode();
    }
    ~Trie (){
        delete root;
    }
    
    void insert(std::string text){
        TrieNode *p = root;
        for(auto ch : text){
            int i = ch - 'a';
            if(p->children[i] == NULL){
                p->children[i] = new TrieNode();
            }
            p = p->children[i];
        }
        p->is_string = true;
    }

    bool search(string text){
        TrieNode *p = root;
        for(auto ch : text){
            int i = ch - 'a';
            if(p->children[i] == NULL){
                return false;
            }
            p = p->children[i];
        }
        
        return p->is_string;
    }
    
    bool startsWith(string prefix) {
        TrieNode *p = root;
        for(auto ch : prefix){
            int i = ch - 'a';
            if(p->children[i] == NULL){
                return false;
            }
            p = p->children[i];
        }

        return true;
    }
private:
    TrieNode *root;
};

Trie 树真的很耗内存吗？

Trie 树是一种非常独特的、高效的字符串匹配方法。但是，关于 Trie 树，有一种说法：“Trie 树是非常耗内存的，用的是一种空间换时间的思路”。这是什么原因呢？

• 上面Trie树的实现时，是用数组来存储一个节点的子节点的指针。如果字符串中包含从a到z这26个字符，那每个节点都要存储一个长度为26的数组，并且每个数组存储一个8字节指针（或者4字节指针，这个大小跟CPU、操作字符、编译器等有关系）。而且，即便一个节点只有很少的子节点，远小于26个，比如3、4个，我们也要维护一个长度为26的数组。
• 而Trie树的本质是避免重复存储一组字符串的相同前缀子串，但是现在每个字符（对应一个节点）的存储远远大于1个字节。按照上面的例子，数组长度为26，每个元素是 8 字节，那每个节点就会额外需要 26*8=208 个字节。而且这还是只包含26 个字符的情况。
• 如果字符串中不仅包含小写字母，还包含大写字母、数字、甚至是中文，那需要的存储空间就更多了。所以，在某些情况下，Trie树不一定会节省存储空间。在重复的前缀并不多的情况下，Trie树不但不能节省内存，还有可能会浪费更多的内存。

Trie树尽管有可能很浪费内存，但是确实非常高效。那为了解决这个内存问题，我们是否有其他办法呢？

• 我们可以稍微牺牲一点查询的效率，将每个节点中的数组换成其他数据结构，来存储一个节点的子节点指针。用哪种数据结构呢？可以用有序数组、跳表、散列表、红黑树等等
• 比如我们用有序数组，数组中的指针按照所指向的字符的大小顺序排列。查询的时候，我们可以通过二分查找的方法，快速查找到某个字符应该匹配的子节点的指针。但是，在往Trie树中插入一个字符串的时候，我们为了维护数组中数据的有序性，就会稍微慢一点

实际上，Trie树的变体有很多，都可以在一定程度上解决内存消耗的问题。比如，缩点优化，就是对只有一个子节点的节点，而且此节点不是一个串的结束节点，可以将此节点与子节点合并。这样可以节省空间，但却增加了编码难度。如下：

Trie 树与散列表、红黑树的比较

实际上，字符串的匹配问题，其实就是数据的查找问题。支持动态数据高效查找的数据结构有散列表、红黑树、跳表等。那它们各种有什么优缺点和应用场景呢？

Trie树对要处理的字符串有着及其严苛的要求：

• 第一，字符串中包含的字符集不能太大。如果字符集太大，那存储空间可能就会浪费很多。即便可以优化，也要付出牺牲查询、插入效率的代价
• 第二，要求字符串的前缀重合比较多，不然空间消耗会变大很多
• 第三，如果要用Trie树解决问题，那我们就要自己从0开始实现一个Trie树，还要保证没有bug，这个在工程上是将简单问题复杂化，除非必须，一般不建议这样做。
• 第四，通过指针串起来的数据块是不连续的，而Trie树中用到了指针，所以，对缓存并不友好，性能上会打个折扣。

因此，针对在一组字符串中查找字符串的问题，在工程中我们倾向用散列表或者红黑树。因为这两种数据结构，我们都不需要自己去实现，直接利用编程语言中提供的现成类库就行了。

实际上，Trie树只是不适合精确匹配查找，这种问题更适合用散列表或者红黑树来解决。Trie树比较适合查找前缀匹配的字符串

小结

• Trie 树是一种解决字符串快速匹配问题的数据结构。如果用来构建 Trie 树的这一组字符串中，前缀重复的情况不是很多，那 Trie 树这种数据结构总体上来讲是比较费内存的，是一种空间换时间的解决问题思路。

• 尽管比较耗费内存，但是对内存不敏感或者内存消耗在接受范围内的情况下，在 Trie 树中做字符串匹配还是非常高效的，时间复杂度是 O(k)，k 表示要匹配的字符串的长度。

• 但是，Trie 树的优势并不在于，用它来做动态集合数据的查找，因为，这个工作完全可以用更加合适的散列表或者红黑树来替代。Trie 树最有优势的是查找前缀匹配的字符串，比如搜索引擎中的关键词提示功能这个场景，就比较适合用它来解决，也是 Trie 树比较经典的应用场景。

• 参考

相关题目

题目
leetcode：208.Trie字典（前缀）树 Implement Trie (Prefix Tree)
leetcode：211. 添加与搜索单词 - 数据结构设计 Add and Search Word - Data structure design
leetcode：642.设计搜索自动补全系统 Design Search Autocomplete System
leetcode：648. 单词替换 replace-words
leetcode：676. 实现一个魔法字典 implement-magic-dictionary
leetcode：677. 键值映射map-sum-pairs