基于波动率模型对上证综指的建模与实证分析
绪论
上海证券综合指数简称“上证指数”或“上证综指”,其样本股是在上海证券交易所全部上市股票,包括A股和B股,反映了上海证券交易所上市股票价格的变动情况,自1991年7月15日起正式发布。
2017年11月23日,A股低开低走,全线深幅调整。上证综指失守3400点整数位,创下年内最大单日跌幅。上一交易日率先回调的深市三大股指同步出现3%以上的跌幅。
上证综合指数是最早发布的指数,是以上证所挂牌上市的全部股票为计算范围,以发行量为权数的加权综合股价指数。这一指数自1991年7月15日起开始实时发布,基日定为1990年12月19日,基日指数定为100点。
中国股票市场虽然起步较晚,但其发展是相当迅猛的,尤其是进入2000年以后,中国的股市更加活跃了。在价格变化多端的股票市场中,投资者们因盲目买卖股票使自己的收益或盈或亏,大多数会带有从众或投机的心理去投资,从而形成一定形式的买卖跟风。股票市场价格序列的残差都具有时变波动性、波动集聚等特点,但是传统的时间序列分析方法无法很好的刻画和解释这一点,恩格尔(Engle)于1982年提出了“条件异方差自回归模型”简称ARCH模型,它能集中地反映方差的变化特点,现已被广泛地应用于经济领域的时间序列分析、验证金融理论中的规律描述、金融市场的预测和决策。因此本文基于ARCH模型结合沪深两证券交易所大盘的收盘价格指数日数据及其波动变化进行实证分析,借鉴国内外专家已有的研究成果,运用极大似然估计方法、ARCH LM检验和残差的白噪声检验等一系列时间序列分析方法,对大盘的日收盘价格指数的波动进行实证分析并对其短期内的走势做出试探性预测。
关键词:上证综指, Arch,Garch,均值模型,波动率模型
- 研究背景
中国股票市场起步的相对于国外的股票市场较晚,但其发展是相当迅猛的。无论是国内还是国外,股票市场的价格序列残差都具有时变波动性、波动集聚等特点,为了能够运用更好的分析方法来解释这一点,许多经济学家开始尝试用不同的模型和方法来解决这个问题。其中具有代表性的是恩格尔(Engle)提出的“条件异方差自回归模型”,简称ARCH模型。因此,利用ARCH类模型分析股票市场的波动特性并对其进行分析具有一定的理论和现实意义。在对股市行情中的研究中,需涉及到时间序列分析这一学科中的ARCH模型分析,经过近二十年的发展,目前该模型已被认为是最集中地反映了方差的变化特点,从而广泛地应用于经济领域的时间序列分析。对金融市场不确定性的探讨和实证分析,是现代金融研究的核心问题之一。近年发展起来的金融市场价格波动非线性时间序列模型及其分析方法,在理论探讨和实际应用方面,都取得迅速的进展,形成了ARCH类计量模型[1]。
- 研究现状
自进入21世纪,中国经济稳健而快速的发展着。我国的证券市场成为经济市场中不可或缺的重要部分[6],越来越具备投资理财意识的现代人把自己的热钱从部分的储蓄里拿出投资到其中,以上海和深圳为代表的股票市场在这样的投资活动中变得更加活跃了。尤其是2006年股市中的投资者们基本上都能盈利,于是更多的人也就跟着进入,形成一定形式的买卖跟风。但是,从2007年美国次贷危机开始席卷各国金融市场,使得中国股票市场在2008年一直处于低迷的熊市状态。许多投资者对此持观望态度,不愿意将热钱倾注于现在的股票市场中。现本文将对我国股票市场的沪深股市的大盘收盘价格指数进行以下的实证分析。
三.数据收集整理
1.数据收集
根据分析所需内容,搜集以下数据:
2005年1月到2018年4月上证综指月度数据
(数据来源:中经网统计数据库)
2.数据整理
将以上数据整理成表:
| time |
closeprice |
time |
closeprice |
| 2005-01 |
1191.82 |
2011-09 |
2359.22 |
| 2005-02 |
1306 |
2011-10 |
2468.25 |
| 2005-03 |
1181.24 |
2011-11 |
2333.41 |
| 2005-04 |
1159.15 |
2011-12 |
2199.42 |
| 2005-05 |
1060.74 |
2012-01 |
2292.61 |
| 2005-06 |
1080.94 |
2012-02 |
2428.49 |
| 2005-07 |
1083.03 |
2012-03 |
2262.79 |
| 2005-08 |
1162.8 |
2012-04 |
2396.32 |
| 2005-09 |
1155.61 |
2012-05 |
2372.23 |
| 2005-10 |
1092.82 |
2012-06 |
2225.43 |
| 2005-11 |
1099.26 |
2012-07 |
2103.63 |
| 2005-12 |
1161.1 |
2012-08 |
2047.52 |
| 2006-01 |
1258.1 |
2012-09 |
2086.17 |
| 2006-02 |
1299 |
2012-10 |
2068.88 |
| 2006-03 |
1298.3 |
2012-11 |
1980.12 |
| 2006-04 |
1440.2 |
2012-12 |
2269.13 |
| 2006-05 |
1641.3 |
2013-01 |
2385.42 |
| 2006-06 |
1672.2 |
2013-02 |
2365.59 |
| 2006-07 |
1612.7 |
2013-03 |
2236.62 |
| 2006-08 |
1658.6 |
2013-04 |
2177.91 |
| 2006-09 |
1752.4 |
2013-05 |
2300.6 |
| 2006-10 |
1838 |
2013-06 |
1979.21 |
| 2006-11 |
2099.3 |
2013-07 |
1993.8 |
| 2006-12 |
2675.5 |
2013-08 |
2098.38 |
| 2007-01 |
2786.3 |
2013-09 |
2174.67 |
| 2007-02 |
2881.1 |
2013-10 |
2141.61 |
| 2007-03 |
3184 |
2013-11 |
2220.5 |
| 2007-04 |
3841.3 |
2013-12 |
2115.98 |
| 2007-05 |
4109.7 |
2014-01 |
2033.08 |
| 2007-06 |
3820.7 |
2014-02 |
2056.3 |
| 2007-07 |
4471 |
2014-03 |
2033.31 |
| 2007-08 |
5218.8 |
2014-04 |
2026.36 |
| 2007-09 |
5552.3 |
2014-05 |
2039.21 |
| 2007-10 |
5954.8 |
2014-06 |
2048.33 |
| 2007-11 |
4871.8 |
2014-07 |
2201.56 |
| 2007-12 |
5261.6 |
2014-08 |
2217.2 |
| 2008-01 |
4383.4 |
2014-09 |
2363.87 |
| 2008-02 |
4348.54 |
2014-10 |
2420.18 |
| 2008-03 |
3472.71 |
2014-11 |
2682.84 |
| 2008-04 |
3693.11 |
2014-12 |
3234.68 |
| 2008-05 |
3433.35 |
2015-01 |
3210.36 |
| 2008-06 |
2736.1 |
2015-02 |
3310.3 |
| 2008-07 |
2775.72 |
2015-03 |
3747.9 |
| 2008-08 |
2397.37 |
2015-04 |
4441.66 |
| 2008-09 |
2293.78 |
2015-05 |
4611.74 |
| 2008-10 |
1728.79 |
2015-06 |
4277.22 |
| 2008-11 |
1871.16 |
2015-07 |
3663.73 |
| 2008-12 |
1820.81 |
2015-08 |
3205.99 |
| 2009-01 |
1990.66 |
2015-09 |
3052.78 |
| 2009-02 |
2082.85 |
2015-10 |
3382.56 |
| 2009-03 |
2373.21 |
2015-11 |
3445.41 |
| 2009-04 |
2477.57 |
2015-12 |
3539.18 |
| 2009-05 |
2632.93 |
2016-01 |
2737.6 |
| 2009-06 |
2959.36 |
2016-02 |
2687.98 |
| 2009-07 |
3412.06 |
2016-03 |
3003.92 |
| 2009-08 |
2667.75 |
2016-04 |
2938.32 |
| 2009-09 |
2779.43 |
2016-05 |
2916.62 |
| 2009-10 |
2995.85 |
2016-06 |
2929.61 |
| 2009-11 |
3195.3 |
2016-07 |
2979.34 |
| 2009-12 |
3277.14 |
2016-08 |
3085.49 |
| 2010-01 |
2989.29 |
2016-09 |
3004.7 |
| 2010-02 |
3051.94 |
2016-10 |
3100.49 |
| 2010-03 |
3109.11 |
2016-11 |
3250.03 |
| 2010-04 |
2870.61 |
2016-12 |
3103.64 |
| 2010-05 |
2592.15 |
2017-01 |
3159.17 |
| 2010-06 |
2398.37 |
2017-02 |
3241.73 |
| 2010-07 |
2637.5 |
2017-03 |
3222.51 |
| 2010-08 |
2638.8 |
2017-04 |
3154.66 |
| 2010-09 |
2655.66 |
2017-05 |
3117.18 |
| 2010-10 |
2978.84 |
2017-06 |
3192.43 |
| 2010-11 |
2820.18 |
2017-07 |
3273.03 |
| 2010-12 |
2808.08 |
2017-08 |
3360.81 |
| 2011-01 |
2790.69 |
2017-09 |
3348.94 |
| 2011-02 |
2905.05 |
2017-10 |
3393.34 |
| 2011-03 |
2928.11 |
2017-11 |
3317.19 |
| 2011-04 |
2911.51 |
2017-12 |
3307.17 |
| 2011-05 |
2743.47 |
2018-01 |
3480.83 |
| 2011-06 |
2762.08 |
2018-02 |
3259.41 |
| 2011-07 |
2701.73 |
2018-03 |
3168.9 |
| 2011-08 |
2567.34 |
2018-04 |
3082.23 |
3.时间序列对象
本数据分析将使用R stdio 3.4.4。
4. .绘制时间序列图
4.1平稳性检验
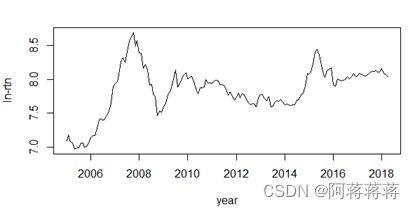
(一)绘制原始上证综指序列的时序图
> da<-read.xlsx("C:/Users/26259/Documents/R/shangzheng2.xlsx")
> head(da)
time closeprice
1 2005-01 1191.82
2 2005-02 1306.00
3 2005-03 1181.24
4 2005-04 1159.15
5 2005-05 1060.74
6 2005-06 1080.94
> closeprice=log(da$closeprice+1)
> rtn=ts(closeprice,frequency = 12,start = c(2005,1))
> plot(rtn,xlab='year',ylab='ln-rtn')
> t.test(closeprice)
One Sample t-test
data: closeprice
t = 278.13, df = 159, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
7.783276 7.894605
sample estimates:
mean of x
7.838941
> Box.test(closeprice,lag=12,type = 'Ljung')
Box-Ljung test
data: closeprice
X-squared = 787.44, df = 12, p-value < 2.2e-16
T.test 和Box.test统计量表明p值接近于0,表明序列没有显著的序列相关性。
4.2模型及方法介绍
4.2.1.建立ARCH模型
ARCH模型建立大致分为以下几步:
步骤(1):通过检验数据的序列相关性建立一个均值方程,如有必要,对收益率序列建立一个计量经济模型(如ARMA)来消除任何线形依赖。
步骤(2):对均值方程的残差进行ARCH效应检验
步骤(3):如果具有ARCH效应,则建立波动率模型
步骤(4):检验拟合的模型,如有必要则进行改进
- 均值模型
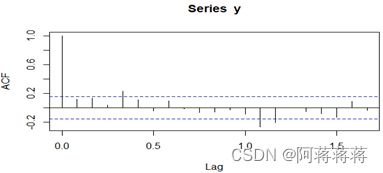
做出acf图,确定模型阶数:
> cp=log(da$closeprice+1)
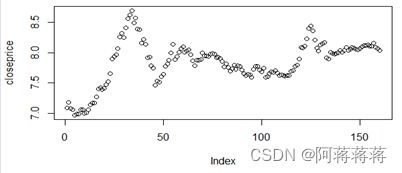
> rtn=ts(cp,frequency = 12,start = c(2005,1))
> plot(rtn,type='1')
> x=diff(rtn,4)
> y=diff(rtn)
> sy=diff(y)
> acf(rtn,lag=20)
> acf(x,lag=20)
> acf(y,lag=20)
> acf(sy)
> m1=arima(rtn,order=c(1,0,0),seasonal=list(order=c(0,1,1),perid=4))
> m1
Call:
arima(x = rtn, order = c(1, 0, 0), seasonal = list(order = c(0, 1, 1), perid = 4))
Coefficients:
ar1 sma1
0.9930 -0.9999
s.e. 0.0216 0.0931
sigma^2 estimated as 0.007215: log likelihood = 139.31, aic = -272.62
Box.test(m1$residuals,lag=12,type = 'Ljung')
Box-Ljung test
data: m1$residuals
X-squared = 25.142, df = 12, p-value = 0.08416
因为对应的Ljung-box统计量的p值>0.05,所以拟合模型能充分描述数据中的序列相关性。
> armamodel=arima(rtn)
> armamodel
Call:
arima(x = rtn)
Coefficients:
intercept
7.8389
s.e. 0.0281
sigma^2 estimated as 0.1263: log likelihood = -61.51, aic = 127.01
(2)由于均值方程为简单的常数加新息,所以用y=rt-r来检验ARCH效应,这里r是rt的样本均值,yt是at的估计。Yt^2的Ljung-Box统计量Q(12)=640.79,其p值接近于0,因此表明它有很强的ARCH效应。
R代码演示:
> y=closeprice-mean(closeprice)
> Box.test(y^2,lag=12,type = 'Ljung')
Box-Ljung test
data: y^2
X-squared = 640.79, df = 12, p-value < 2.2e-16
(3)模型估计和检验
> library(fGarch)
载入需要的程辑包:timeDate
载入需要的程辑包:timeSeries
载入需要的程辑包:fBasics
> resi=(residuals(m1,standardize=T))
> acf(resi,lag=20)
> pacf(resi,lag=20)
从PACF图中,我们看出在间隔为1,2,16上有显著的相关性,为保持模型简单,我们对波动率建立一个ARCH(2)模型,相应地,我们为上证综指月度数据建立以下形式的波动率模型: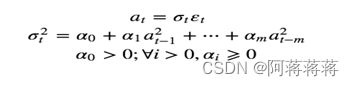
假定εt是独立同分布的标准正态序列,我们得到的拟合模型是:
Rt=7.9875+at, δt^2=0.0040+0.9999a2t-1+0.0001 a2t-2
其中,各个参数估计值的标准误差分别是3.529e-02,2.225e-03,2.034e-01,2.182e-01,参见下面的R输出结果,尽管估计值满足ARCH(3)模型的一般要求,但α2的估计值在0.05的水平下不是统计显著的,因此模型可以简化。
R代码演示:
> m1=garchFit(~1+garch(2,0),data=closeprice,trace = F)
> summary(m1)
Title:
GARCH Modelling
Call:
garchFit(formula = ~1 + garch(2, 0), data = closeprice, trace = F)
Mean and Variance Equation:
data ~ 1 + garch(2, 0)
[data = closeprice]
Conditional Distribution:
norm
Coefficient(s):
mu omega alpha1 alpha2
7.98749489 0.00401985 0.99999999 0.00000001
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 7.987e+00 3.529e-02 226.368 < 2e-16 ***
omega 4.020e-03 2.225e-03 1.807 0.0708 .
alpha1 1.000e+00 2.034e-01 4.916 8.82e-07 ***
alpha2 1.000e-08 2.182e-01 0.000 1.0000
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Log Likelihood:
17.0278 normalized: 0.1064237
Description:
Mon May 21 08:35:54 2018 by user: 26259
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 8.015361 0.01817551
Shapiro-Wilk Test R W 0.9294648 4.455211e-07
Ljung-Box Test R Q(10) 403.6291 0
Ljung-Box Test R Q(15) 408.2778 0
Ljung-Box Test R Q(20) 409.9474 0
Ljung-Box Test R^2 Q(10) 7.758695 0.6523939
Ljung-Box Test R^2 Q(15) 9.657796 0.8406957
Ljung-Box Test R^2 Q(20) 13.44348 0.8575561
LM Arch Test R TR^2 6.52695 0.8872287
Information Criterion Statistics:
AIC BIC SIC HQIC
-0.16284745 -0.08596811 -0.16405729 -0.13162941
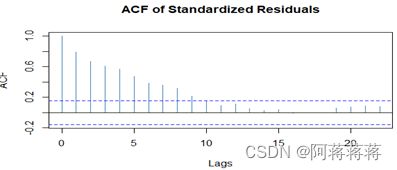
图4-4显示的是标准化的残差,PACF图表明在标准化残差的平方序列的高阶间隔上仍然有序列相关性。
标准化残差at的Ljung-Box统计量为Q(10)=403.63,p值为0,而Q(20)=409.95,p值为0,at2的Ljung-Box统计量为Q(10)=7.76,p=-0.65,at2的Ljung-Box统计量为Q(20)=13.44,p=0.85.因此,如果只是关注高阶的模型,那么在0.05的显著性水平下,ARCH(2)模型就能充分地描述给定数据的条件异方差性。
> "archTest" <- function(rtn,m=10){
+ # Perform Lagrange Multiplier Test for ARCH effect of a time series
+ # rtn: time series
+ # m: selected AR order
+ #
+ y=(rtn-mean(rtn))^2
+ T=length(rtn)
+ atsq=y[(m+1):T]
+ x=matrix(0,(T-m),m)
+ for (i in 1:m){
+ x[,i]=y[(m+1-i):(T-i)]
+ }
+ md=lm(atsq~x)
+ summary(md)
+ }
> archTest(closeprice)
Call:
lm(formula = atsq ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.20795 -0.01912 -0.00575 0.01437 0.22267
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.009183 0.005444 1.687 0.09389 .
x1 0.980898 0.080897 12.125 < 2e-16 ***
x2 0.176958 0.114598 1.544 0.12482
x3 -0.502028 0.114311 -4.392 2.21e-05 ***
x4 0.319990 0.120080 2.665 0.00861 **
x5 0.064114 0.120771 0.531 0.59635
x6 -0.322010 0.120827 -2.665 0.00861 **
x7 0.129510 0.119943 1.080 0.28212
x8 0.078734 0.112441 0.700 0.48496
x9 -0.176240 0.108607 -1.623 0.10691
x10 0.119150 0.073997 1.610 0.10962
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.05265 on 139 degrees of freedom
Multiple R-squared: 0.8772, Adjusted R-squared: 0.8684
F-statistic: 99.3 on 10 and 139 DF, p-value: < 2.2e-16
ARCH效应检验表明上证综指月度序列有显著的ARCH效应。
(4)画图
> plot(m1)
Make a plot selection (or 0 to exit):
1: Time Series
2: Conditional SD
3: Series with 2 Conditional SD Superimposed
4: ACF of Observations
5: ACF of Squared Observations
6: Cross Correlation
7: Residuals
8: Conditional SDs
9: Standardized Residuals
10: ACF of Standardized Residuals
11: ACF of Squared Standardized Residuals
12: Cross Correlation between r^2 and r
13: QQ-Plot of Standardized Residuals
5.总结及建议
5.1 我国股市存在异方差性
从上海证券交易所的收盘价格指数波动的统计特征呈现出明显的尖峰厚尾特征及残差的线图,到ARCH LM检验出的结果,可看出我国股市是存在很强的异方差性的。
5.2 ARCH类模型能够消除股市异方差
通过时间序列分析的ARCH模型和GARCH模型能够很好的描述大盘股票收盘价格指数波动变化的尖峰厚尾特征,经过ARCH LM检验及残差平方图的显示,发现大盘股价收盘指数的异方差性确实是被消除了。对于此,ARCH模型能够更加广泛的应用于股票市场行情的分析中。
参考文献
[1] (美)博迪等著,朱宝宪等译.投资学[M]. 北京:机械工业出版社,2007.12
[2] 胡海鹏,方兆本.股市波动性预测模型改进研究[J].数理统计与管理,2004(9)
[3] 郑梅,苗佳,王升.预测沪深股市市场波动性[J],系统工程理论与实践,2005
[4] 唐小凤.ARCH模型在金融市场中的应用[J].数学研究,2007.3
[5] 严定琪,李育锋.基于GARCH族模型的沪深300指数波动率预测[J].兰州交通大学学报,2008(2)