&4_单机优化(确定性算法,优化框架)
优化框架
- 机器学习的优化框架
-
- 正则化经验风险最小化
- 优化算法的收敛速率
- 假设条件
-
- 凸函数定义
- 强凸函数定义
- 光滑函数定义
- 优化算法的分类
机器学习的优化框架
正则化经验风险最小化
有监督的机器学习问题:
假设输入输出数据 S n = { ( x i , y i ) ; i = 1 , . . . , n } S_n = \left\{(x_i, y_i); i = 1, ..., n\right\} Sn={(xi,yi);i=1,...,n} 是依据输入输出空间 X × Y X \times Y X×Y 上的真实分布 P x , y P_{x,y} Px,y 独立同分布地随机生成的。
学习的目标:找到输入输出之间的函数映射关系,即预测模型 g ( ⋅ ; w ) g(· ; w) g(⋅;w) ,其中w是模型g的参数。
为方便叙述,有时会把参数w所对应的预测模型简称为模型w。
对于新的输入x,希望所习得的模型g能够给出足够接近真实输出y的预测结果 g ( x ; w ) g(x; w) g(x;w)。
预测的好坏:用损失函数 l ( w ; x , y ) l(w ; x,y) l(w;x,y) 来衡量。
对于真实分布 P x , y P_{x,y} Px,y未知,我们依据训练数据 S n S_n Sn来学习预测模型g。 假设训练过程遵循正则化经验风险最小化原则,也就是,我们希望预测模型g在训练数据上的平均损失函数值(即经验风险)尽可能小;同时,我们对模型g的复杂度进行惩罚,防止过拟合。
正则化经验风险最小化(R-ERM)问题的目标函数可以表达如下:
l ^ n ( w ) = 1 n ∑ i = 1 n l ( w ; x i , y i ) + λ R ( w ) \hat{l}_n(w) = \frac{1}{n} \sum_{i=1}^{n}l(w;x_i,y_i)+\lambda R(w) l^n(w)=n1i=1∑nl(w;xi,yi)+λR(w)
其中, R ( ⋅ ) R(·) R(⋅)是对于模型w的正则项(比如 L 2 L_2 L2正则 R ( w ) = ∣ ∣ w ∣ ∣ 2 2 R(w)=||w||_{2}^{2} R(w)=∣∣w∣∣22)
由于在优化算法的运行过程中,训练数据已经生成并保持固定,为了讨论方便且在不影响严格性的情形下,我们将上述R-ERM目标函数关于训练数据的符号进行简化,如下:
f ( w ) = 1 n ∑ i = 1 n f i ( w ) f(w) = \frac{1}{n} \sum_{i=1}^{n}f_i(w) f(w)=n1i=1∑nfi(w)
其中, f i ( w ) = l ( w ; x i , y i ) + λ R ( w ) f_i(w) = l(w;x_i,y_i)+\lambda R(w) fi(w)=l(w;xi,yi)+λR(w) 是模型w在第i各训练样本 ( x i , y i ) (x_i, y_i) (xi,yi)上的正则损失函数。不同的优化算法采用不同的方法对上述目标函数进行优化,以寻找最优的预测模型。
看似殊途同归,但实践中的性能和效果可能有很大差别。其中,最主要的是优化算法的收敛性和收敛速率。
优化算法的收敛速率
假设优化算法在其结束时的第T步迭代中输出的模型是 w T w_T wT,R-ERM问题的最优模型为 w ∗ = arg min w f ( w ) w^*=\arg \min_wf(w) w∗=argminwf(w)。
一个有效的的优化算法会随着迭代的进行使输出的模型 w T w_T wT越来越接近于最优模型 w ∗ w^* w∗。
二者的接近程度通常用它们在参数空间中的距离或者它们对应的正则化经验风险的差值来衡量,即
E = ∣ ∣ w T − w ∗ ∣ ∣ 2 ⩽ ε ( T ) E =||w_T-w^*||^2 \leqslant \varepsilon (T) E=∣∣wT−w∗∣∣2⩽ε(T) 或者 E f ( w T ) − f ( w ∗ ) ⩽ ε ( T ) Ef(w_T) - f(w^*) \leqslant \varepsilon (T) Ef(wT)−f(w∗)⩽ε(T)
如果 ε ( T ) → 0 \varepsilon (T)\rightarrow0 ε(T)→0,那么优化算法是收敛的。对于收敛的优化算法,它们的收敛速率可能并不相同。通常,用 log ε ( T ) \log \varepsilon (T) logε(T) 的衰减速率来定义优化算法的收敛速率:
- 如果 log ε ( T ) \log \varepsilon (T) logε(T)与-T同阶,称该算法具有线性收敛速率;
- 如果 log ε ( T ) \log \varepsilon (T) logε(T)比-T衰减速度慢,称该算法具有次线性收敛速率;
- 如果 log ε ( T ) \log \varepsilon (T) logε(T)比-T衰减速度快,称该算法具有超线性收敛速率;
- 如果 log log ε ( T ) \log\log \varepsilon (T) loglogε(T)与-T同阶,称该算法具有二阶收敛速率。
然而,正则化风险最小化的优化算法并不一定总是收敛的,需要目标函数具有相对良好的性质,为此要引入一些基本的假设条件。
假设条件
目前大多数关于优化算法的收敛性质都需要依赖目标函数具有某些良好的数学属性,比如凸性和光滑性。
凸性:刻画的是函数的一种几何性质:直观上,凸性要求函数在自变量的任何取值处的切线都在函数曲面下方。
光滑性:刻画了函数变化的缓急程度。直观上,如果自变量的微小变化只会引起函数值的微小变化,则称这个函数是光滑的。对于可导和不可导函数,这个直观性质有不同的数学定义。对于不可导函数,通常用Lipschitz性质来描述光滑性。
凸函数定义
考虑实值函数 f : R d → R f: R^d\rightarrow R f:Rd→R,如果对任意自变量w, v ∈ R d v \in R^d v∈Rd都有下面不等式成立:
f ( w ) − f ( v ) ⩾ ▽ f ( v ) T ( w − v ) f(w) -f(v) \geqslant \triangledown f(v)^T(w-v) f(w)−f(v)⩾▽f(v)T(w−v)
则称函数f是凸的。
凸性会给优化带来很大的方便:凸函数的任何一个局部极小值都是全局最优解。
强凸函数定义
考虑实值函数 f : R d → R f: R^d\rightarrow R f:Rd→R和 R d R^d Rd上的模 || · ||,如果对任意自变量w, v ∈ R d v \in R^d v∈Rd都有下面不等式成立:
f ( w ) − f ( v ) ⩾ ▽ f ( v ) T ( w − v ) + α 2 ∣ ∣ w − v ∣ ∣ 2 f(w) -f(v) \geqslant \triangledown f(v)^T(w-v)+ \frac{\alpha }{2}||w-v||^2 f(w)−f(v)⩾▽f(v)T(w−v)+2α∣∣w−v∣∣2
则称函数 f f f关于模 || · || 是 α − \alpha- α− 强凸的。
函数 f f f是 α − \alpha- α− 强凸的当且仅当 f − α 2 ∣ ∣ ⋅ ∣ ∣ 2 f-\frac{\alpha }{2}||·||^2 f−2α∣∣⋅∣∣2是凸的。
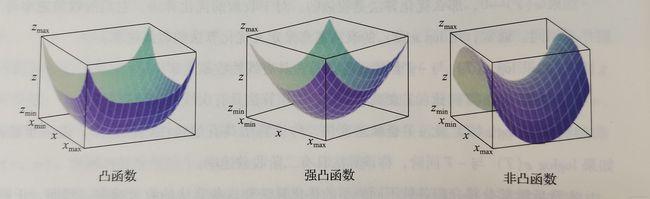
光滑函数定义
考虑实值函数 f : R d → R f: R^d\rightarrow R f:Rd→R和 R d R^d Rd上的模 || · ||,如果存在常数 β > 0 \beta >0 β>0,对任意自变量w, v ∈ R d v \in R^d v∈Rd都有下面不等式成立:
f ( w ) − f ( v ) ⩾ ▽ f ( v ) T ( w − v ) + β 2 ∣ ∣ w − v ∣ ∣ 2 f(w) -f(v) \geqslant \triangledown f(v)^T(w-v)+ \frac{\beta }{2}||w-v||^2 f(w)−f(v)⩾▽f(v)T(w−v)+2β∣∣w−v∣∣2
则称函数 f f f关于模 || · || 是 β − \beta- β− 光滑的。
凸函数 f f f是 β − \beta- β− 光滑的充分必要条件为其导数 ▽ f \triangledown f ▽f是 β − L i p s c h i t z \beta- Lipschitz β−Lipschitz 连续的。
所以, β − \beta- β−光滑的函数的光滑性质比Lipschitz联系的函数的光滑性质要更好。
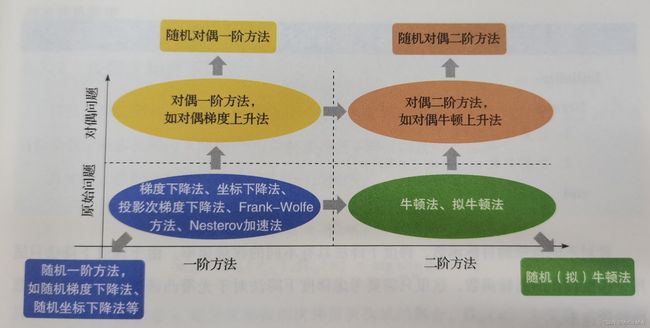
优化算法的分类
随着机器学习问题中数据规模不断增大,优化问题的复杂度不断增高,越来越多的优化算法发展出随机版本和并行化版本。
为更好地对众多优化算法进行分析,对其进行如下分类: