机器学习—无监督学习（一）KMeans聚类

机器学习—无监督学习（一）KMeans聚类

---

---

前言

最近在学习python机器学习，做了几个相关的比赛正好专业也有相关的课程。在浅浅记录一下学习的过程，和大家分享，欢迎大家批评指正啦！

---

提示：以下是本篇文章正文内容，下面案例仅供参考

一、无监督学习？

无监督学习意味着数据集只包含一个部分：描述对象/事件的特征向量。 如果没有真实标签，我们希望使用样本之间的相似性对数据进行聚类，以最小化类内差距并最大化类间差距。 一般来说，在实际应用中，很多情况下，样本的标签是无法提前知道的，也就是说训练样本没有对应的类别，所以分类器设计只能从原始样本集中学习 没有样品标签。。

二、用k-均值进行相似性分组

聚类是一种能够找到相似对象的一种分析方法，例如在爱奇艺中对不同的电影主题进行分组；或者通过顾客的购物清单发现有相同兴趣的客户。找到实物的内在联系，在茫茫人海中发现你，即为聚类；

k-均值算法是无监督聚类算法中的经典之作，也是目前较热的无监督学习算法。其算法极易实现、计算效率较高，属于基于原型聚类的范畴。

1、什么是基于原型的聚类？

基于原型的聚类呢？顾名思义，意味着每一个类相应的都对应一个原型。那么问题接踵而至，什么是原型？（怎么这么多问题！！！）我们刚才提到无监督学习的training dataset中只包含描述对象/事件的特征向量，所以那原型就是每一类中最能代表此类特征的特征。对于连续特征而言，原型为平均值，而对于分类的离散特征而言，则为类中心——最能代表此类的特征点。k-均值算法擅长识别球型集群：

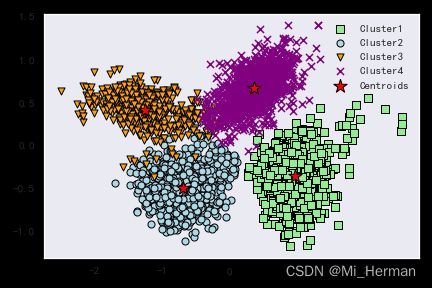
但需要指出的是：k-均值算法是先验算法，所以在使用前需要指出集群数K。K值得选择将很大程度上决定了其算法的聚类性能，在下面得示例演示中我会简单使用一种elbow方法来评估和确定集群上数目K。

2.k-均值算法流程

1）随机从样本中挑选k个质心作为初始集群质心（elbow或silhouette plot）；
2）将每个样本分配到最近得质心；
3）把质心移到已分配样本的中央；
4）重复步骤2、3，直到集群赋值不再改变，或者tol值或最大迭代次数达到最大；

3.度量对象之间相似性

既然聚类的任务是把具有相似特征的事件或物品分为一类，那么如何确定数据之间的相似性呢？

这里，我们可以把相似性定义为特征间距离的倒数。对于m维空间中x和y两点之间的常用距离是其两点间欧式距离的平方：

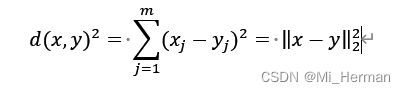
基于欧式距离度量，我们可以将k-means算法描述为一种简单的优化问题，是一种最小化群内的SSE的迭代方法，也被称为惯性集群（cluster inertia):

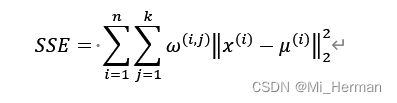
对于样本Xi，如果其在集群j中，则令w(i,j) = 1，否则为0；
接下来，我们将采用scikit-learn cluster模块对KMeans算法进行简单应用；

三、利用Python简单实现k-均值算法：

1.导入数据：

为了方便可视化分析，利用sklearn datasets模块随机创建一个二维数据集：

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
X,y = make_blobs(n_samples = 3000,n_features = 2,centers = 4,cluster_std = 0.6,shuffle = True,random_state = 0)# 创建随机数据集

对于初始数据集我们利用matplotlib对数据集分布有一个初步的印象：

plt.scatter(X[:,0],X[:,1],c = 'lightblue', marker= 'o',edgecolors='black',s = 50)
plt.grid()
plt.tight_layout()
plt.savefig("CSDN_KMEANS初始数据集.png")plt.scatter(X[y_km == 0,0],X[y_km == 0,1],s = 50, c = 'lightgreen', marker= 's',edgecolors='black',label = 'Cluster1')
plt.scatter(X[y_km == 1,0],X[y_km == 1,1],s = 50, c = 'lightblue', marker= 'o',edgecolors='black',label = 'Cluster2')
plt.scatter(X[y_km == 2,0],X[y_km == 2,1],s = 50, c = 'orange', marker= 'v',edgecolors='black',label = 'Cluster3')
plt.scatter(X[y_km == 3,0],X[y_km == 3,1],s = 50, c = 'purple', marker= 'x',edgecolors='black',label = 'Cluster4')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s = 200, c = 'red', marker= '*',edgecolors='black',label = 'Centroids')
plt.legend(scatterpoints = 1)
plt.grid()
plt.tight_layout()
# plt.savefig('CSDN-Cluster_results.png')
plt.show()
plt.show()

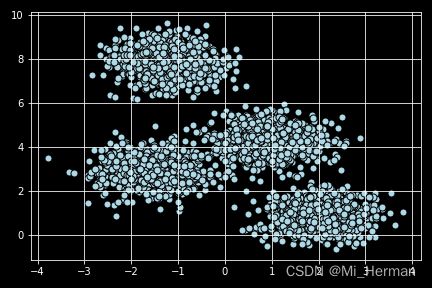
通过初步印象，认为n_cluster = 4 应该是一个不错的选择，但是这是依靠经验而谈，缺少数据的支撑接下来看看对于此简单二维数据，如何确定其集群数K。

2、利用肘部方法（elbow）确定集群数量K

作为无监督分类的最大挑战及和K-均值聚类之间最大的矛盾在于k-均值是一种先验算法，需要率先知道K值的大小，因此我们需要一个可以确定其聚类性能的指标，在这里我们用到的是前文提到的SSE（集群内失真）来比较不同K值下的聚类性能；

对于scikit-learn中可以通过调用KMeans中的intertia_来访问SSE，不需要自定义计算：
简言之，如果k增大，失真会减小；而肘部方法就是利用此寻找失真增速最快的k值，因此绘制不同k值下的失真图就会更加直观的挑选合适的k值：

from sklearn.cluster import KMeans
distortions = []
for i in range(1,11):
    km = KMeans(n_clusters=i,init='random',n_init=10,max_iter=300,tol=1e-04,random_state=0)
    km= KMeans(n_clusters=i)
    km.fit(X)
    distortions.append(km.inertia_)
plt.plot(range(1,11),distortions,marker = 'o')
plt.xlabel('number of clusters')
plt.ylabel('Disortion')
plt.tight_layout()
plt.savefig('CSDN-elbow_figure.png')plt.scatter(X[y_km == 0,0],X[y_km == 0,1],s = 50, c = 'lightgreen', marker= 's',edgecolors='black',label = 'Cluster1')
plt.scatter(X[y_km == 1,0],X[y_km == 1,1],s = 50, c = 'lightblue', marker= 'o',edgecolors='black',label = 'Cluster2')
plt.scatter(X[y_km == 2,0],X[y_km == 2,1],s = 50, c = 'orange', marker= 'v',edgecolors='black',label = 'Cluster3')
plt.scatter(X[y_km == 3,0],X[y_km == 3,1],s = 50, c = 'purple', marker= 'x',edgecolors='black',label = 'Cluster4')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s = 200, c = 'red', marker= '*',edgecolors='black',label = 'Centroids')
plt.legend(scatterpoints = 1)
plt.grid()
plt.tight_layout()
# plt.savefig('CSDN-Cluster_results.png')
plt.show()
plt.show()

结果如图：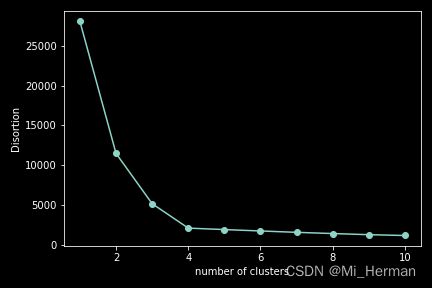
显然n = 4是一个不错的选择，对于不断增加的K虽然其值仍在减小，但是变化不大，反而会出现其他error，因此，我们选择 K = 4；

3、对数据集进行聚类

扫除了最大的K-均值算法中最大的障碍，下面我们对上述数据集进行聚类：

km = KMeans(n_clusters=4,init='random',n_init=10,max_iter=300,tol=1e-04,random_state=0)
y_km = km.fit_predict(X)

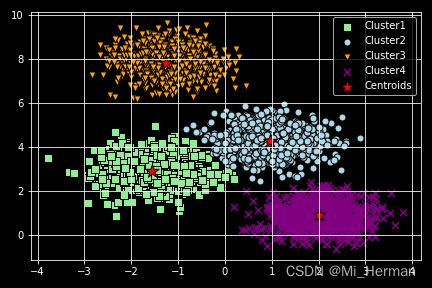
利用matplotlib画出聚类结果：

plt.scatter(X[y_km == 0,0],X[y_km == 0,1],s = 50, c = 'lightgreen', marker= 's',edgecolors='black',label = 'Cluster1')
plt.scatter(X[y_km == 1,0],X[y_km == 1,1],s = 50, c = 'lightblue', marker= 'o',edgecolors='black',label = 'Cluster2')
plt.scatter(X[y_km == 2,0],X[y_km == 2,1],s = 50, c = 'orange', marker= 'v',edgecolors='black',label = 'Cluster3')
plt.scatter(X[y_km == 3,0],X[y_km == 3,1],s = 50, c = 'purple', marker= 'x',edgecolors='black',label = 'Cluster4')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s = 200, c = 'red', marker= '*',edgecolors='black',label = 'Centroids')
plt.legend(scatterpoints = 1)
plt.grid()
plt.tight_layout()
# plt.savefig('CSDN-Cluster_results.png')
plt.show()

写在最后

当然，K-Means算法只是在无监督学习聚类算法中较为常见的一种方法，后续还会更新其他的聚类方法，更高维数据的聚类方法等。希望小伙伴们一起学习一起进步呀！！！！冲冲冲！！！！

Reference

【1】Sebastian Raschka, Vahid Mirjalili Python Machine Learning /third edition/