Games101:作业6解析(含提高部分SAH)
目录
1、作业概览
2、更新Render和Triangle
2.1 Render
2.2 getIntersection
3、IntersectP
4、getIntersection
5、SAH
6、参考链接
1、作业概览
2、更新Render和Triangle
对于本次作业,其实初看起来是有点让人没有头绪的,我建议先看一看上次已经写好的代码,定位到原来的框架,如果你能正确更新,那么就能对这次要做的任务有一个具体的认识了。
2.1 Render
首先来说一下render.cpp的Render函数,其作用是从光源到屏幕依次发出若干条光线。在本次作业中老师给出的框架已经写上了基本的计算,需要更新的是对于frame的赋值方式,此时可以发现render.cpp已经没有原本的castRay函数了,但是在scene.cpp中定义了同名的castRay函数,是不是一样的?可以看一下上次作业中castRay部分的注释及代码,它实现的功能是从摄像机的位置经过当前像素位置发出一条光线,判断光线达到物体的位置的材质,由此确定光线作用方式并确定颜色,而对比可以发现此时Scene中的castRay函数方法也是一样的。当然其实直接比较代码也可以看出来,二者结构基本一致,唯一的不同在于参数,在此次作业中,需要传的参数为一个Ray结构的变量和depth。
我个人认为depth类似于“视深”,在后续的代码中对于可以反光的材质如会发生反射、折射或者透明的材质,会继续递归调用castRay并且把depth+1,而在最初又规定了可处理的depth的最大深度,故我认为这里反映了一个像素已反射其他像素的次数,即当前的光线是第几层次的间接光源,程序设定的最大depth为5,故一个像素点最多能显示五次光线反射的效果。
而Ray结构,则需要去看此次新定义出的Ray.hpp,了解一下该数据类型的初始化方式以及参数列表、相关方法等:光线类,包含一条光的源头、方向、传递时间 t,并且重定义了()运算符,在其中传入传递时间,即可返回当前光线所在位置。想要初始化定义Ray结构变量至少要传入光源位置和方向,也可传入传递时间,其默认值为0,所以此时光源位置即为照相机eye_pos,方向是算出来的dir,即可轻易定义出Ray。
另外由于此时castRay是scene.cpp定义的方法,所以需要用Scene类型的变量调用该方法,最终代码如下:
// The main render function. This where we iterate over all pixels in the image,
// generate primary rays and cast these rays into the scene. The content of the
// framebuffer is saved to a file.
void Renderer::Render(const Scene& scene)
{
std::vector framebuffer(scene.width * scene.height);
float scale = tan(deg2rad(scene.fov * 0.5));
float imageAspectRatio = scene.width / (float)scene.height;
Vector3f eye_pos(-1, 5, 10);
int m = 0;
for (uint32_t j = 0; j < scene.height; ++j) {
for (uint32_t i = 0; i < scene.width; ++i) {
// generate primary ray direction
float x = (2 * (i + 0.5) / (float)scene.width - 1) *
imageAspectRatio * scale;
float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
// TODO: Find the x and y positions of the current pixel to get the
// direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable
// *scale*, and x (horizontal) variable with the *imageAspectRatio*
// Don't forget to normalize this direction!
Vector3f dir = normalize(Vector3f(x, y, -1)); // Don't forget to normalize this direction!
// ori = eye_pos
Ray ray(eye_pos, dir, 0);
// castRay函数位置改变
framebuffer[m++] = scene.castRay(ray, 0);
}
UpdateProgress(j / (float)scene.height);
}
UpdateProgress(1.f);
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
} 2.2 getIntersection
该函数的作用是计算光线与三角形相交的交点,更新与上面的处理方式基本相同。首先定位这个函数在Triangle.hpp中,给出的框架已经把三角形相交需要计算的各个参数进行了判断,命名方式可能与公式有所不同但计算流程都是一样的,并且对于没有相交的情况都直接返回了初始状态的inter值,现只需关注t_tmp即光线传播的时间即可。
函数最终要返回intersection类型的变量,那么需要看一下这个变量应该怎么定义和赋值。
struct Intersection
{
Intersection(){
happened=false;
coords=Vector3f();
normal=Vector3f();
distance= std::numeric_limits::max();
obj =nullptr;
m=nullptr;
}
bool happened;
Vector3f coords;
Vector3f normal;
double distance;
Object* obj;
Material* m;
};
#endif //RAYTRACING_INTERSECTION_H 如上,关键的属性值即为happened(是否相交),coords(交点坐标),normal(交点所在平面法线),distance(光线起点到交点的距离),obj(交点所在物体的物体类型),m(交点所在物体的材料类型)。
要想正确定义所有变量,就要靠当前函数getIntersection中已计算出来的值和当前类Triangle中本身定义的值:
happened,很好判断,既然各种条件判断都没有问题,则相交已发生,直接赋值为true即可
coords,交点坐标,即光线原点+t*光线方向,可直接利用Ray函数重定义的()符号操作的得到。
normal,交点所在平面法线,即当前的小三角形的法线,即Triangle中的normal。
distance,距离即可为t_tmp。
obj,注意Object类型本身是一个超类,具体的object类型有三个,一个是Sphere,一个是Triangle,一个是MeshTriangle,而此时的obj即为当前的三角形面类型,引用自身this。
class Sphere : public Object
class Triangle : public Object
class MeshTriangle : public Objectm,材质,与三角形面本身保持一致,为Triangle中的 m。
代码如下:
inline Intersection Triangle::getIntersection(Ray ray)
{
Intersection inter;
if (dotProduct(ray.direction, normal) > 0)
return inter;
double u, v, t_tmp = 0;
//S1
Vector3f pvec = crossProduct(ray.direction, e2);
//分母
double det = dotProduct(e1, pvec);
//接近0
if (fabs(det) < EPSILON)
return inter;
double det_inv = 1. / det;
//S
Vector3f tvec = ray.origin - v0;
//b1
u = dotProduct(tvec, pvec) * det_inv;
if (u < 0 || u > 1)
return inter;
//S2
Vector3f qvec = crossProduct(tvec, e1);
//b2
v = dotProduct(ray.direction, qvec) * det_inv;
if (v < 0 || u + v > 1)
return inter;
//t
t_tmp = dotProduct(e2, qvec) * det_inv;
// TODO find ray triangle intersection
if(t_tmp < 0)
return inter;
inter.happened = true;
inter.coords = ray(t_tmp);
inter.normal = normal;
// 距离用时间代替
inter.distance = t_tmp;
inter.obj = this;
inter.m = m;
return inter;
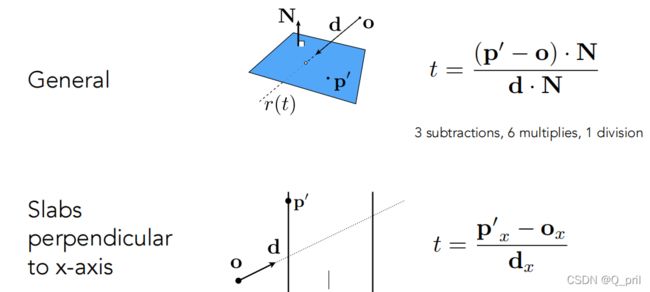
}3、IntersectP
这一部分是为了判断光线能否与当前的包围盒相交,判断方法为计算当前光线到达包围盒的最短时间和最长时间,比较是否满足:![]() &&
&& ![]()
要写好这一部分代码,需要好好阅读Bounds3的各个属性值,可以知道一个包围盒有8个点,每个点由(x,y,z)3个值表示,同时它也是有上下、左右、前后6组平面围成的,所以x,y,z各有2个值,总共8种组合、8个点,pMin和pMax即为包围盒的斜对角分别记录了最小的(x1,y1,z1)和最大的(x2,y2,z2)
class Bounds3
{
public:
//bounds的斜对角,详见第三个初始化函数
Vector3f pMin, pMax; // two points to specify the bounding box
Bounds3()
{
double minNum = std::numeric_limits::lowest();
double maxNum = std::numeric_limits::max();
pMax = Vector3f(minNum, minNum, minNum);
pMin = Vector3f(maxNum, maxNum, maxNum);
}
Bounds3(const Vector3f p) : pMin(p), pMax(p) {}
Bounds3(const Vector3f p1, const Vector3f p2)
{
pMin = Vector3f(fmin(p1.x, p2.x), fmin(p1.y, p2.y), fmin(p1.z, p2.z));
pMax = Vector3f(fmax(p1.x, p2.x), fmax(p1.y, p2.y), fmax(p1.z, p2.z));
} 所以对于每一组平面都需要分别计算一个最小时间和最大时间,代入公式即可,这里的invDir分别记录了光线传播沿xyz方向的倒数,便于计算公式中的 “÷某一传播方向” 。另外,pMin和pMax记录的数值上的大小,但光线传播方向不同的情况下计算的最短、最长时间不一样,需要再矫正一下,具体代码如下:
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
const std::array& dirIsNeg) const
{
// invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z),
// use this because Multiply is faster that Division
// dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)],
// use this to simplify your logic
// TODO test if ray bound intersects
float t_Min_x = (pMin.x - ray.origin.x)*invDir[0];
float t_Min_y = (pMin.y - ray.origin.y)*invDir[1];
float t_Min_z = (pMin.z - ray.origin.z)*invDir[2];
float t_Max_x = (pMax.x - ray.origin.x)*invDir[0];
float t_Max_y = (pMax.y - ray.origin.y)*invDir[1];
float t_Max_z = (pMax.z - ray.origin.z)*invDir[2];
//dirIsNeg表面光线的方向,如果是正方向则为1,pmin-O为最短路径
//反之为负方向0,pmax-O是最短路径
if(!dirIsNeg[0])
{
float t = t_Min_x;
t_Min_x = t_Max_x;
t_Max_x = t;
}
if(!dirIsNeg[1])
{
float t = t_Min_y;
t_Min_y = t_Max_y;
t_Max_y = t;
}
if(!dirIsNeg[2])
{
float t = t_Min_z;
t_Min_z = t_Max_z;
t_Max_z = t;
}
float t_enter = std::max(t_Min_x,std::max(t_Min_y,t_Min_z));
float t_exit = std::min(t_Max_x,std::min(t_Max_y,t_Max_z));
if(t_enter=0)
return true;
else
return false;
} 4、getIntersection
该部分用于计算分出的包围盒是否相交,要正确写出这部分的代码最好先理解一下BVHBuildNode* BVHAccel::recursiveBuild函数,其作用在于递归建造包围盒,首先判断当前空间中的物体个数,如果是1个或者2个可以直接建立1个或2个叶节点,否则先分出当前空间中最长的轴,再将这个轴从中间分开,递归处理左边和右边部分的物体们,为它们建立包围盒。
再来看getIntersection函数,其参数分别为当前BVH树的节点和光线,对于节点node,先看其结构,分为当前节点的包围盒,左子树和右子树,当前包围盒内部物体类型(三角形等)。
struct BVHBuildNode {
Bounds3 bounds;
BVHBuildNode *left;
BVHBuildNode *right;
Object* object;
public:
int splitAxis=0, firstPrimOffset=0, nPrimitives=0;
// BVHBuildNode Public Methods
BVHBuildNode(){
bounds = Bounds3();
left = nullptr;right = nullptr;
object = nullptr;
}
};那么计算节点和光线的交点分为以下情况:
1、当前节点所代表的大的包围盒与光线无交点:
则左右子树也不比再计算,可直接返回空交点
2、当前节点所代表的大的包围盒与光线有交点:
2.1、当前节点为叶子节点:
只需判断其包围盒内部的物体是否与光线相交
2.2、当前节点还含有左右子树:
递归判断左右子树的包围盒情况
这里提示一点,判断当前包围盒和光线相交与否时,需要调用IntersectP,这个函数是Bounds3的方法,所以由Node->bounds调用;而计算包围盒内部物体是否与光线相交需要利用Object的方法,即getIntersection,它被写在每一个继承Object类的类里,如Triangle,Sphere等等;对于递归情况则需要对于左右子树分别再次调用当前的getIntersection。
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
// TODO Traverse the BVH to find intersection
std::array dirIsNeg;
dirIsNeg[0] = (ray.direction[0]>0);
dirIsNeg[1] = (ray.direction[1]>0);
dirIsNeg[2] = (ray.direction[2]>0);
Intersection inter;
// 对于任意结点,如果其boundbox与光线无交点,则不需进一步的判断,
// 否则依次递归,直到叶子节点,判断叶子节点中存的各个物体如三角形、球形等是否与光线有交点
if(!node->bounds.IntersectP(ray,ray.direction_inv,dirIsNeg)){
return inter;
}
if(node->left == nullptr && node->right == nullptr){
return node->object->getIntersection(ray);
}
Intersection l = getIntersection(node->left,ray);
Intersection r = getIntersection(node->right,ray);
// 返回距离光源进的物体的相交信息
return l.distance 5、SAH
提高部分采用SAH处理包围盒建造过程,具体原理可以见参考链接,这里简单概括一下。
SAH是基于表面积的启发式评估划分方法(Surface Area Heuristic,SAH),因为有时候当物体分布不均匀时,划分结果可能会导致包围盒之间有很多重叠,这种重叠会导致后续求交冗余,而求交的代价要比遍历物体划分包围盒的代价高的多,所以这种方法即通过对求交代价和遍历代价进行评估,给出了每一种划分的代价(Cost),而我们的目的便是去寻找代价最小的划分。
所以该算法的核心在于使求交代价最低,而对于某一个大的包围盒,求交代价取决于当前包围盒的大小(影响光线击中包围盒的概率)和包围盒中的物体个数(多少个物体就意味着要求交多少次),现用表面积来代表包围盒大小并假设对每个物体求交的代价是相同的(设为1),并设遍历当前所有包围盒的代价为0.125(因为遍历代价小于求交代价),则可以得到:
如果对于每个结点,每次遍历所有包围盒再决定当前的划分方式则:
BVHBuildNode* BVHAccel::recursiveBuild(std::vector objects)
{
// 通过树形结构,划分物体以此划分包围盒
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
//计算根节点的所有bounds
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
else if (objects.size() == 2) {
node->left = recursiveBuild(std::vector{objects[0]});
node->right = recursiveBuild(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else {
Bounds3 centroidBounds;
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
// 交换选择纬度错切分,划分子节点
int dim = centroidBounds.maxExtent();
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
// 递归分离节点
auto beginning = objects.begin();
auto middling = objects.begin() + (objects.size() / 2);
auto ending = objects.end();
bool SAH = true;
if(SAH){
// 递归分离节点
auto size = objects.size();
int proper_cut = 0;
double mintime = 0x3f3f3f;
for(int index=0; index(beginning, middling);
auto rightshapes = std::vector(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
Bounds3 leftBounds,rightBounds;
// time = S_1面积 /S_0面积 *S_1空间物体数 * t_obj
// + S_2面积 /S_0面积 *S_2空间物体数 * t_obj
for (int i = 0; i < leftshapes.size(); ++i)
leftBounds =
Union(leftBounds, leftshapes[i]->getBounds().Centroid());
for (int i = 0; i < rightshapes.size(); ++i)
rightBounds =
Union(rightBounds, rightshapes[i]->getBounds().Centroid());
auto leftS = leftBounds.SurfaceArea();
auto rightS = rightBounds.SurfaceArea();
auto S = leftS + rightS;
auto time = leftS / S * leftshapes.size() + rightS / S * rightshapes.size();
if(time(beginning, middling);
auto rightshapes = std::vector(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
return node;
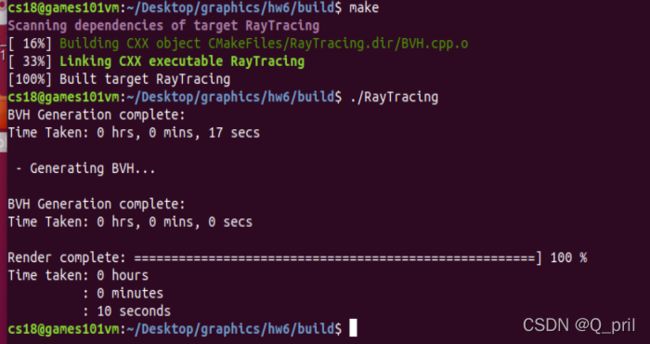
} 这样会导致BVH生成变得很慢(0—>17s),但是渲染过程会快约2s(12—>10s):
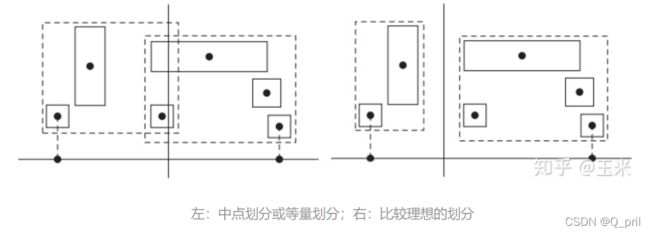
所以,在实现的时候,相比于计算可能划分的代价然后寻找代价最小的划分,一种更好的办法是将节点所包围的空间沿着跨度最长的那个坐标轴的方向将空间均等的划分为若干个桶(Buckets),划分只会出现在桶与桶之间的位置上。如图所示,若桶的个数为 n 则只会有 n-1 种划分的可能。
BVHBuildNode* BVHAccel::recursiveBuild(std::vector objects)
{
// 通过树形结构,划分物体以此划分包围盒
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
//计算根节点的所有bounds
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
else if (objects.size() == 2) {
node->left = recursiveBuild(std::vector{objects[0]});
node->right = recursiveBuild(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else {
Bounds3 centroidBounds;
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
// 交换选择纬度错切分,划分子节点
int dim = centroidBounds.maxExtent();
switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
// 递归分离节点
auto beginning = objects.begin();
auto middling = objects.begin() + (objects.size() / 2);
auto ending = objects.end();
bool SAH = true;
if(SAH){
// 递归分离节点
int part = 10;
auto size = objects.size();
int proper_cut = 0;
double mintime = 0x3f3f3f;
for(int index=0; index(beginning, middling);
auto rightshapes = std::vector(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
Bounds3 leftBounds,rightBounds;
// time = S_1面积 /S_0面积 *S_1空间物体数 * t_obj
// + S_2面积 /S_0面积 *S_2空间物体数 * t_obj
for (int i = 0; i < leftshapes.size(); ++i)
leftBounds =
Union(leftBounds, leftshapes[i]->getBounds().Centroid());
for (int i = 0; i < rightshapes.size(); ++i)
rightBounds =
Union(rightBounds, rightshapes[i]->getBounds().Centroid());
auto leftS = leftBounds.SurfaceArea();
auto rightS = rightBounds.SurfaceArea();
auto S = leftS + rightS;
auto time = leftS / S * leftshapes.size() + rightS / S * rightshapes.size();
if(time(beginning, middling);
auto rightshapes = std::vector(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
}
return node;
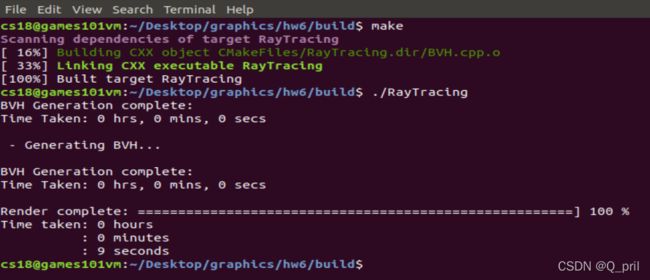
} 速度如下所示:
最终结果如图,是否使用SAH不影响图的结果:
6、参考链接
PBRT-E4.3-层次包围体(BVH)(一) - 知乎