DeeplabV3+解码器复现
1.全局通道注意力
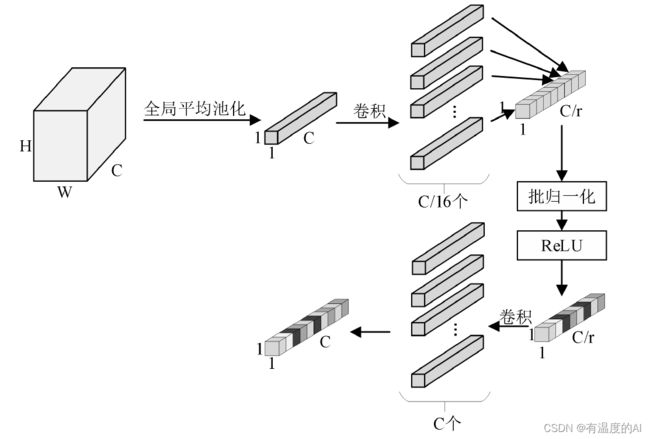
全局通道注意力结构可以使神经网络在训练过程中建模特征图各个通道的重要性,自动判断哪些通道上的信息为有用信息,哪些通道上的信息为噪声信息。全局通道注意力结构以SENet的通道注意力结构为基础,添加了批归一化和ReLU激活用于调整权重分布,残差结构增强了模型对强噪声和高冗余数据的处理能力。全局通道注意力模块的输入为尺寸为H×W×C的特征图X,输出为维度是1×1×C的通道权重矩阵。
class global_SE(nn.Module):
# 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接下降通道的倍数
def __init__(self, in_channel, ratio=16):
# 继承父类初始化方法
super(global_SE, self).__init__()
# 全局平均池化,输出的特征图的宽高=1
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
self.conv1 = nn.Sequential(
nn.Conv2d(in_channel, in_channel // ratio, kernel_size=1, stride=1, padding=0),
nn.BatchNorm2d(in_channel // ratio),
nn.ReLU()
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channel // ratio, in_channel, kernel_size=1, stride=1, padding=0),
)
def forward(self, inputs): # inputs 代表输入特征图
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
x = self.avg_pool(inputs)
x = self.conv1(x)
x = self.conv2(x)
return x2.局部通道注意力
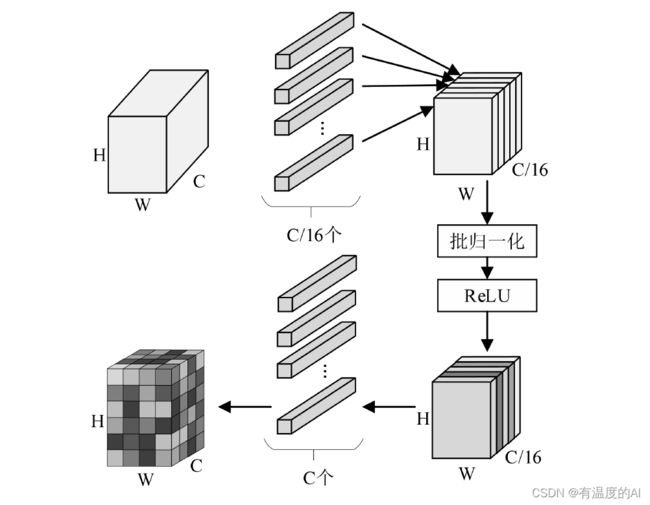
局部通道注意力与全局通道注意力相似,输入同样为H×W×C的特征图,输出为维相同维度的通道权重矩阵。局部通道注意力模块没有对输入特征图进行全局平均池化,直接采用1×1卷积将输入特征图的通道数降为原来的1/16。通过卷积建模各通道间的相关性,并将特征图通道数恢复为C。
class local_SE(nn.Module):
def __init__(self, in_channel):
super(local_SE, self).__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(in_channel, in_channel//16, kernel_size=1, stride=1, padding=0),
nn.BatchNorm2d(in_channel // 16),
nn.ReLU()
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channel // 16, in_channel, kernel_size=1, stride=1, padding=0),
)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
return x3.多尺度通道注意力
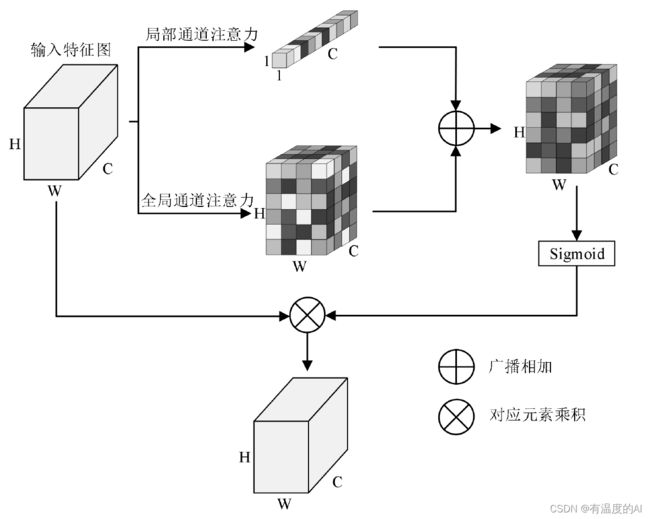
多尺度通道注意力整合区局通道信息和局部通道信息,可以提高神经网络对小尺度目标的关注度,降低特征融合过程中的噪声干扰,提升图像语义分割算法的鲁棒性。
class global_SE(nn.Module):
# 初始化, in_channel代表输入特征图的通道数, ratio代表第一个全连接下降通道的倍数
def __init__(self, in_channel, ratio=16):
# 继承父类初始化方法
super(global_SE, self).__init__()
# 全局平均池化,输出的特征图的宽高=1
self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
self.conv1 = nn.Sequential(
nn.Conv2d(in_channel, in_channel // ratio, kernel_size=1, stride=1, padding=0),
nn.BatchNorm2d(in_channel // ratio),
nn.ReLU()
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channel // ratio, in_channel, kernel_size=1, stride=1, padding=0),
)
def forward(self, inputs): # inputs 代表输入特征图
# 全局平均池化 [b,c,h,w]==>[b,c,1,1]
x = self.avg_pool(inputs)
x = self.conv1(x)
x = self.conv2(x)
return x
class local_SE(nn.Module):
def __init__(self, in_channel):
super(local_SE, self).__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(in_channel, in_channel//16, kernel_size=1, stride=1, padding=0),
nn.BatchNorm2d(in_channel // 16),
nn.ReLU()
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channel // 16, in_channel, kernel_size=1, stride=1, padding=0),
)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
return x
class scSE(nn.Module):
def __init__(self, in_channel, ratio=16):
super(scSE, self).__init__()
self.cSE = global_SE(in_channel,ratio)
self.sSE = local_SE(in_channel)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
res = self.cSE(x) + self.sSE(x)
resul = self.sigmoid(res)
return x * resul
4.多尺度特征融合过程
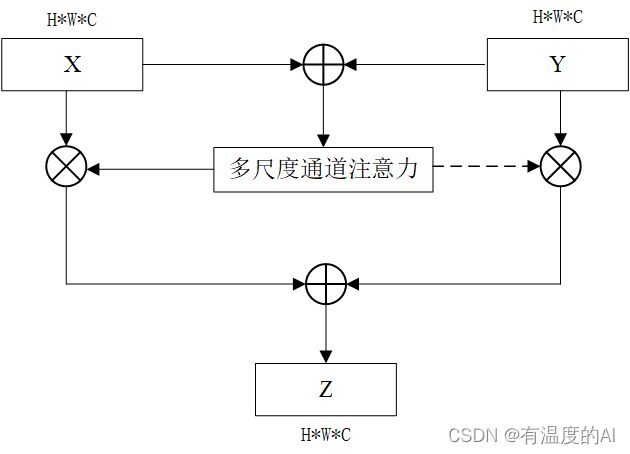
首先将输入特征进行对应元素相加经过多尺度通道注意力模块获取通道权重矩阵,记为M。使用通道权重矩阵分别对中的通道重要程度进行引导,最后将Add操作后的特征图作为通道注意力机制特征融合模块的输出。
虚线表示1-M,通道权重矩阵M中的值由0~1的数组成,1-M中值的范围也是0~1。这种计算方式等价于对输入特征X和Y中对应元素做加权平均,均衡了输入特征所携带信息所占比重。
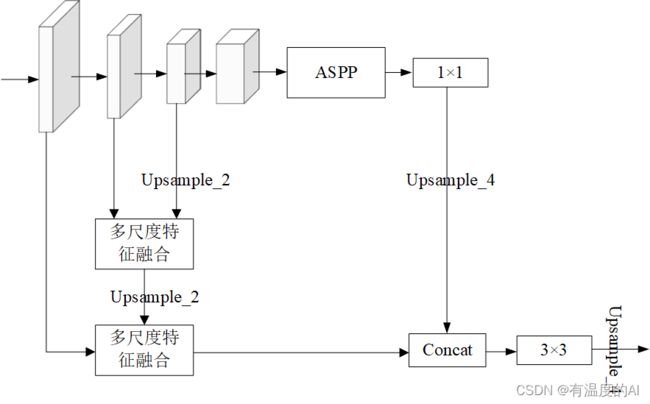
5.解码器设计one
def forward(self, x):
H, W = x.size(2), x.size(3)
low_level_features, the_three_features, the_four_features, x = self.backbone(x)
x = self.aspp(x) #32*32*256
x1 = F.interpolate(x, size=(low_level_features.size(2), low_level_features.size(3)),
mode='bilinear', align_corners=True) # 32*32*256-128*128*256
the_four_features1 = F.interpolate(the_four_features, size=(the_three_features.size(2), the_three_features.size(3)),
mode='bilinear', align_corners=True) #32*32*64-64*64*64
the_three_features0 = self.down_conv1(the_three_features) #64*64*32-64*64*64
F1 = the_three_features0 + the_four_features1 #64*64*64
# print(F1)
# print(F1.shape)
M = self.scSE(F1) #64*64*64
Z = M * the_three_features0 + (1-M) * the_four_features1 #64*64*64
Z1 = F.interpolate(Z,size=(low_level_features.size(2), low_level_features.size(3)),
mode='bilinear', align_corners=True) #64*64*64-128*128*64
low_level_features1 = self.down_conv0(low_level_features) #128*128*24-128*128*64
F2 = low_level_features1 + Z1 #128*128*64
M2 = self.scSE(F2) #128*128*64
Z2 = M2 * low_level_features1 + (1-M2) * Z1 #128*128*64
x2 = torch.cat((x1, Z2), dim=1) #128*128*320
x3 = self.cat_conv(x2) #128*128*320-128*128*256
x4 = self.cls_conv(x3) #128*128*256-128*128*cla_num
x5 = F.interpolate(x4, size=(H, W), mode='bilinear', align_corners=True)
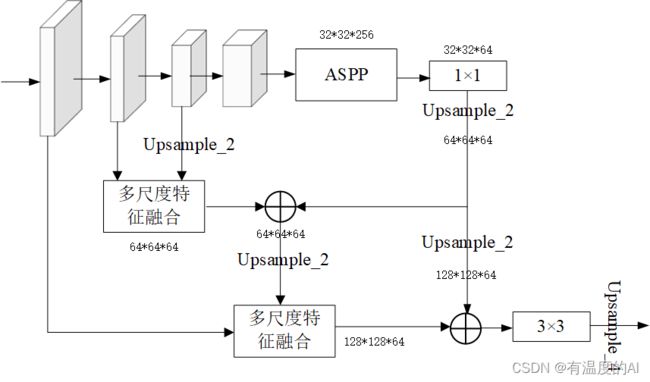
return x56.解码器设计two
def forward(self, x):
H, W = x.size(2), x.size(3)
low_level_features, the_three_features, the_four_features, x = self.backbone(x)
x = self.aspp(x) #32*32*256
x1_0 = self.downaspp(x) # 32*32*256-32*32*64
x1 = F.interpolate(x1_0, size=(the_three_features.size(2), the_three_features.size(3)),
mode='bilinear', align_corners=True) #32*32*64-64*64*64
# -----------------------------------------#
the_four_features1 = F.interpolate(the_four_features, size=(the_three_features.size(2), the_three_features.size(3)),
mode='bilinear', align_corners=True) #32*32*64-64*64*6
the_three_features0 = self.down_conv1(the_three_features) #64*64*32-64*64*64
F1 = the_three_features0 + the_four_features1 #64*64*64
# print(F1)
# print(F1.shape)
M = self.scSE(F1) #64*64*64
Z = M * the_three_features0 + (1-M) * the_four_features1 #64*64*64
# -----------------------------------------#
Z0 = Z + x1 #64*64*64
# -----------------------------------------#
Z1 = F.interpolate(Z0,size=(low_level_features.size(2), low_level_features.size(3)),
mode='bilinear', align_corners=True) #64*64*64-128*128*64
low_level_features1 = self.down_conv0(low_level_features) #128*128*24-128*128*64
F2 = low_level_features1 + Z1 #128*128*64
M2 = self.scSE(F2) #128*128*64
Z2 = M2 * low_level_features1 + (1-M2) * Z1 #128*128*64
# -----------------------------------------#
x1_1 = F.interpolate(x1, size=(low_level_features.size(2), low_level_features.size(3)),
mode='bilinear', align_corners=True) #64*64*64-128*128*64
x2 = x1_1 + Z2 #128*128*64
x3 = self.cls_conv(x2) #128*128*64-128*128*cla_num
x4 = F.interpolate(x3, size=(H, W), mode='bilinear', align_corners=True)
return x4