数据结构与算法

统一声明：
博客转载 声 明 ： 本博客部分内容来源于网络、书籍、及各类手册。
        内容宗旨为方便查询、总结备份、开源分享。
        部分转载内容均有注明出处，如有侵权请联系博客告知并删除，谢谢！
百度云盘提取码：统一提取码： ziyu

个人网站入口：http://www.baiziqing.cn/

一、基本概念

1.1、数据结构起源

由于最初涉及的运算对象是简单的整型、实型或布尔型数据，所以程序设计者的主要精力集中于程序设计的技巧上，而无需重视数据结构。随着计算机应用领域的扩大和软硬件的发展，非数值计算问题显得越来越重要。

据统计，当今处理非数值计算问题占用了90%以上的机器时间。
这类问题涉及的数据结构更为复杂，数据元素之间的相互关系一般无法用数学方程式加以描述。因此，解决这类问题的关键不再是数学分析和计算方法，而是要设计出合适的数据结构。

所以，数据结构是一门研究非数值计算的程序设计问题中的操作对象，以及它们之间的关系和操作等相关问题的学科。

1968年，美国DonaldEKnuth教授在其所写的《计算机程序艺术》第一卷《基本算法》中，较系统地阐述了数据的逻辑结构和存储结构以及操作，开创了“数据结构”的课程体系。同年，数据结构作为一门独立课程，在计算机科学学位课程中开始出现。

数据结构是介于数学、计算机硬件、计算机软件、逻辑学等学科之间的综合学科，是计算机学科的一门核心课程，是设计实现编译系统、操作系统、数据库等其他课程和大型应用程序的基础。

进入70年代，出现了大型计算机程序，软件开始相对独立，结构程序设计成为程序设计方法学的主要内容。

程序设计的实质是对实际问题设计/选择好的数据结构和好的算法，
而好的算法在很大程度上取决于描述实际问题的数据结构。

著名的瑞士计算机科学家沃思（N.Wirth）教授曾提出：
程序设计 = 数据结构 + 算法

1.2、数据结构

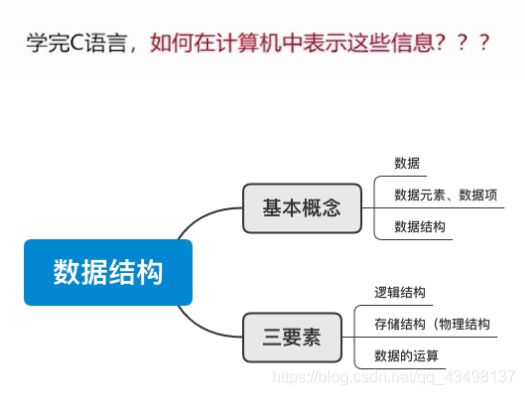
1.3、数据结构基本概念

正所谓“巧妇难为无米之炊”，数据结构是针对数据进行研究的学科，那么这里的“米”就是数据。

数据不仅仅包含整型、字符型、浮点型等数值类型，还包括字符、图像、声音、视频等非数值类型。

数据元素：例如，若我们要对家畜类进行调查，则牛、羊、马、狗、猪等都是家畜类的数据元素。
数据项： 例如，人这样的数据元素，可以有眼、耳、鼻、口、手等数据项，也可以有姓名、年龄、性别、出生日期、出生地址、联系电话等数据项。具体使用哪些数据项，要视你做的程序决定。

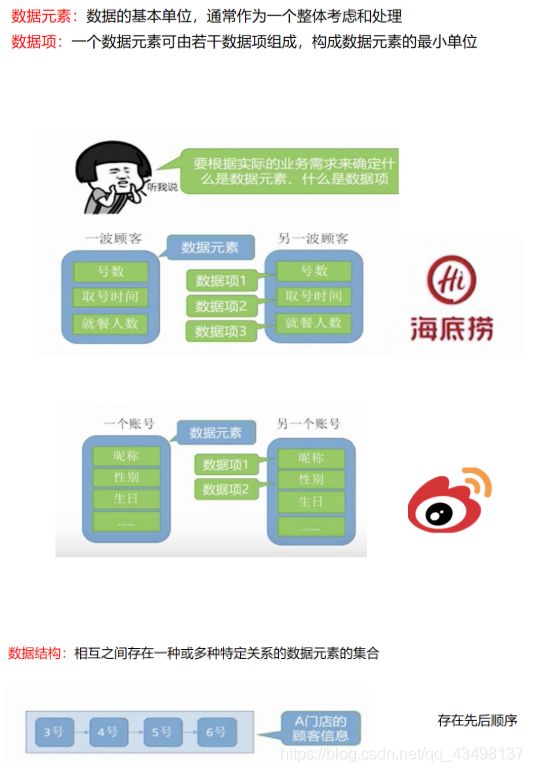
• 数据：描述客观事实的符号，能被计算机所识别、操作，并输入到计算机中的一些符号的集合，信息的载体
• 数据项：一个数据元素可由若干数据项组成，构成数据元素的最小单位
• 数据元素：数据基本单位，通常作为一个整体考虑和处理
• 数据结构：相互之间存在一种或多种特定关系的数据元素的结合

1.4、数据结构三要素

1.4.1. 逻辑结构： 线性、树形、图状

1.4.2. 存储结构：顺序存储、链式存储

1.4.3. 数据的运算：增删改查

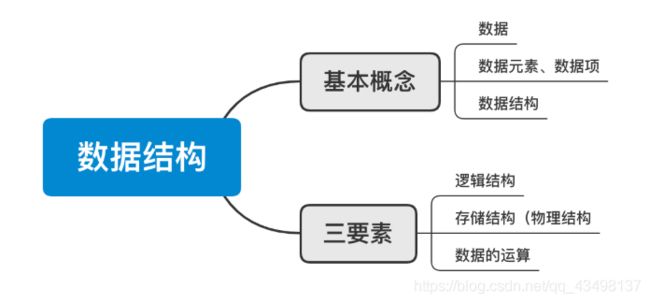
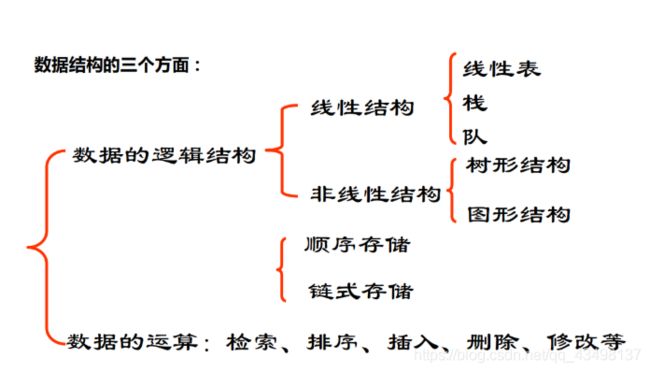
1.5、数据结构三个方面

二、线性表（逻辑结构）

2.1、线性表的概念

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。
线性结构：一对一

假设有n个数据元素，满足线性结构；
特点：1.n = 0， 该表为空
   2.a0为表头，没有直接前驱， a（n-1），表尾，没有直接后继
   3.其他有且仅有一个直接前驱和一个直接后继

顺序存储结构存放线性表：顺序表
链式存储结构存放线性表：链表

2.2、顺序表

2.2.1、顺序表运算：
顺序表初始化：
  typedef struct list{
    int data[size];
    int last;
  }seqlist;

2.2.2、静态分配：
如果“数组”放满怎么办？
如果刚开始就声明一个内存空间呢？

2.2.3、动态分配：
int *p = (int *)malloc(3 * sizeof(int));

2.2.4、顺序表的基本运算：
初始化
判空
判满
求表长
插入
删除
查找
修改
清空
销毁
输出

2.2.5、顺序表的实现
（1）seqlist_malooc.c

#include 
#include 
#include 
#include 

#define SIZE 100

typedef int data_t;		//重命名int 类型

//顺序表
typedef struct list{
	data_t data[SIZE];	//数组，用来存放数据元素
	int last;		//最后一个元素下标
}seqlist;			//重命名，struct list == seqlist，结构体的数据类型

//初始化
seqlist *creatSeqlist()
{
	//动态分配
	seqlist *seq = (seqlist *)malloc(sizeof(seqlist));//结构体指针
	if(seq == NULL)
	{
		printf("malloc failed!\n");
		return NULL;
	}

	memset(seq->data, 0, sizeof(seq->data));//把结构体的成员data数组清零
	seq->last = -1;	//如果下标为-1，说明顺序表中没有元素存在

	return seq;
}

//判空
int seqlist_is_empty(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last == -1)?1:0);
}

//判满
int seqlist_is_full(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last+1 == SIZE)?1:0);
}

//求表长
int seqlist_length(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return (seq->last+1);
}

//插入：按位置插入数据元素
int inserSeqlistByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)			//malloc是否成功
		return -1;

	if(seqlist_is_full(seq) == 1)	//判满
		return -1;

	int len = seqlist_length(seq);	//插入的位置
	if(pos < 0 || pos > len)
		return -1;

	int i = 0;
	for(i= seq->last; i>=pos; i--)
	{
		seq->data[i+1] = seq->data[i];
	}
	seq->data[pos] = data;
	seq->last++;
}

//删除：按位置删除数据元素
int deleteSeqlistByPos(seqlist *seq, int pos)
{
	if(NULL == seq)
		return -1;

	if(seqlist_is_empty(seq) == 1)	//判空
		return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	int i = 0;

	for(i=pos; i<seq->last; i++)
	{
		seq->data[i] = seq->data[i+1];
	}
	seq->last--;
}

//查找：按位置来查找数据元素
data_t findSeqlistByPos(seqlist * seq, int pos)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	return seq->data[pos];
}

//修改：按位置来修改数据元素
int changSeqlisByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;
	
	seq->data[pos] = data;	//按位置来修改数据元素
}

//查找：按值来查找数据元素,返回那个值的下标
int findSeqlistByData(seqlist *seq, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
		return -1;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		if(seq->data[i] == data)
		{
			return i;
		}
	}
}

//删除：按值来删除数据元素
int deleteSeqlistByData(seqlist *seq, data_t data)
{
	int pos = findSeqlistByData(seq, data);

	deleteSeqlistByPos(seq, pos);
}

//修改：按值来修改数据元素
int changeSeqlistByData(seqlist *seq, data_t old_data, data_t new_data)
{
	int pos = findSeqlistByData(seq, old_data);

	changSeqlisByPos(seq, pos, new_data);
}

//清空
void clearSeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	seq->last = -1;
}

//销毁：把地址的地址回收掉
void destroySeqlist(seqlist **seq)
{
	free(*seq);

	*seq = NULL;
}

//输出
void displaySeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	if(seqlist_is_empty(seq) == 1)
		return ;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		printf("%d ", seq->data[i]);
	}

	puts(" ");
}

int main(int argc, const char *argv[])
{
	seqlist *seq = creatSeqlist();
	if(seq == NULL)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = seqlist_is_empty(seq);
	printf("line:%d, n:%d\n",__LINE__, n);			//：line:221, n:1

	int m = seqlist_is_full(seq);
	printf("line:%d, m:%d\n",__LINE__, m);			//：line:224, n:0

	int len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);		//：line:227, n:0

	//按位置插入数据元素
	int i = 0;
	while(i<10)
	{
		inserSeqlistByPos(seq, i, i+1);			
		i++;
	}
	len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);		//： 10
	//打印输出
	displaySeqlist(seq);							//：1 2 3 4 5 6 7 8 9 10 

	//按位置删除
	deleteSeqlistByPos(seq, 2);
	//打印输出
	displaySeqlist(seq);							//：1 2 4 5 6 7 8 9 10 

	//按位置来查找数据元素
	data_t data = findSeqlistByPos(seq, 5);
	printf("data = %d\n", data);					//：data = 7

	//按位置来修改数据元素
	changSeqlisByPos(seq, 1, 250);
	//打印yy输出
	displaySeqlist(seq);							//：1 250 4 5 6 7 8 9 10

	//查找：按值来查找数据元素,返回那个值的下标
	int pos = findSeqlistByData(seq, 250);
	printf("line:%d, pos = %d\n", __LINE__, pos);	//：line:257, pos = 1

	//删除：按值来删除数据元素
	deleteSeqlistByData(seq, 7);
	displaySeqlist(seq);							//：1 250 4 5 6 8 9 10

	//修改：按值来修改数据元素
	changeSeqlistByData(seq, 10, 100);
	displaySeqlist(seq);							//：1 250 4 5 6 8 9 100

	//清空
	clearSeqlist(seq);
	displaySeqlist(seq);							//：
	len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);		//：line:271, n:0

	//销毁
	destroySeqlist(&seq);
	printf("seq = %p\n", seq);						//：seq = (nil)

	return 0;
}										

（2）seqlist_static.c

#include 
#include 
#include 
#include 

#define SIZE 100

typedef int data_t;		//重命名int 类型

//顺序表
typedef struct list{
	data_t data[SIZE];	//数组，用来存放数据元素
	int last;		//最后一个元素下标
}seqlist;			//重命名，struct list == seqlist，结构体的数据类型

//判空
int seqlist_is_empty(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last == -1)?1:0);
}

//判满
int seqlist_is_full(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last+1 == SIZE)?1:0);
}

//求表长
int seqlist_length(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return (seq->last+1);
}

//插入：按位置插入数据元素
int inserSeqlistByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)			//malloc是否成功
		return -1;

	if(seqlist_is_full(seq) == 1)	//判满
		return -1;

	int len = seqlist_length(seq);	//插入的位置
	if(pos < 0 || pos > len)
		return -1;

	int i = 0;
	for(i= seq->last; i>=pos; i--)
	{
		seq->data[i+1] = seq->data[i];
	}
	seq->data[pos] = data;
	seq->last++;
}

//插入：按位置插入数据元素
int deleteSeqlistByPos(seqlist *seq, int pos)
{
	if(NULL == seq)
		return -1;

	if(seqlist_is_empty(seq) == 1)	//判空
		return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	int i = 0;

	for(i=pos; i<seq->last; i++)
	{
		seq->data[i] = seq->data[i+1];
	}
	seq->last--;
}

//查找：按位置来查找数据元素
data_t findSeqlistByPos(seqlist * seq, int pos)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	return seq->data[pos];
}

//修改：按位置来修改数据元素
int changSeqlisByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;
	
	seq->data[pos] = data;	//按位置来修改数据元素
}

//查找：按值来查找数据元素,返回那个值的下标
int findSeqlistByData(seqlist *seq, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
		return -1;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		if(seq->data[i] == data)
		{
			return i;
		}
	}
}

//删除：按值来删除数据元素
int deleteSeqlistByData(seqlist *seq, data_t data)
{
	int pos = findSeqlistByData(seq, data);

	deleteSeqlistByPos(seq, pos);
}

//修改：按值来修改数据元素
int changeSeqlistByData(seqlist *seq, data_t old_data, data_t new_data)
{
	int pos = findSeqlistByData(seq, old_data);

	changSeqlisByPos(seq, pos, new_data);
}

//清空
void clearSeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	seq->last = -1;
}

//输出
void displaySeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	if(seqlist_is_empty(seq) == 1)
		return ;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		printf("%d ", seq->data[i]);
	}

	puts(" ");
}

int main(int argc, const char *argv[])
{
	//静态分配，定义一个结构体变量即可
	seqlist seq = {{0},-1};

	int n = seqlist_is_empty(&seq);
	printf("line:%d, n:%d\n",__LINE__, n);

	int m = seqlist_is_full(&seq);
	printf("line:%d, n:%d\n",__LINE__, m);

	int len = seqlist_length(&seq);
	printf("line:%d, n:%d\n",__LINE__, len);

	//按位置插入数据元素
	int i = 0;
	while(i<10)
	{
		inserSeqlistByPos(&seq, i, i+1);
		i++;
	}
	len = seqlist_length(&seq);
	printf("line:%d, n:%d\n",__LINE__, len);
	//打印输出
	displaySeqlist(&seq);

	//按位置删除
	deleteSeqlistByPos(&seq, 2);
	//打印输出
	displaySeqlist(&seq);

	//按位置来查找数据元素
	data_t data = findSeqlistByPos(&seq, 5);
	printf("data = %d\n", data);

	//按位置来修改数据元素
	changSeqlisByPos(&seq, 1, 250);
	//打印yy输出
	displaySeqlist(&seq);

	//查找：按值来查找数据元素,返回那个值的下标
	int pos = findSeqlistByData(&seq, 250);
	printf("line:%d, pos = %d\n", __LINE__, pos);

	//删除：按值来删除数据元素
	deleteSeqlistByData(&seq, 7);
	displaySeqlist(&seq);

	//修改：按值来修改数据元素
	changeSeqlistByData(&seq, 10, 100);
	displaySeqlist(&seq);

	//清空
	clearSeqlist(&seq);
	displaySeqlist(&seq);
	len = seqlist_length(&seq);
	printf("line:%d, n:%d\n",__LINE__, len);

	return 0;
}							

（3）模块化编程
seqlist.h

#ifndef _SEQLIST_H
#define _SEQLIST_H

#include 
#include 
#include 
#include 

#define SIZE 100

typedef int data_t;		//重命名int 类型

//顺序表
typedef struct list{
	data_t data[SIZE];	//数组，用来存放数据元素
	int last;		//最后一个元素下标
}seqlist;			//重命名，struct list == seqlist，结构体的数据类型


//初始化
seqlist *creatSeqlist();

//判空
int seqlist_is_empty(seqlist *seq);

//判满
int seqlist_is_full(seqlist *seq);

//求表长
int seqlist_length(seqlist *seq);

//插入：按位置插入数据元素
int inserSeqlistByPos(seqlist *seq, int pos, data_t data);

//插入：按位置插入数据元素
int deleteSeqlistByPos(seqlist *seq, int pos);

//查找：按位置来查找数据元素
data_t findSeqlistByPos(seqlist * seq, int pos);

//修改：按位置来修改数据元素
int changSeqlisByPos(seqlist *seq, int pos, data_t data);

//查找：按值来查找数据元素,返回那个值的下标
int findSeqlistByData(seqlist *seq, data_t data);

//删除：按值来删除数据元素
int deleteSeqlistByData(seqlist *seq, data_t data);

//修改：按值来修改数据元素
int changeSeqlistByData(seqlist *seq, data_t old_data, data_t new_data);

//清空
void clearSeqlist(seqlist *seq);

//销毁：把地址的地址回收掉
void destroySeqlist(seqlist **seq);

//输出
void displaySeqlist(seqlist *seq);

#endif												

seqlist.c

#include 
#include 
#include 
#include 

#include "seqlist.h"

//初始化
seqlist *creatSeqlist()
{
	//动态分配
	seqlist *seq = (seqlist *)malloc(sizeof(seqlist));//结构体指针
	if(seq == NULL)
	{
		printf("malloc failed!\n");
		return NULL;
	}

	memset(seq->data, 0, sizeof(seq->data));//把结构体的成员data数组清零
	seq->last = -1;	//如果下标为-1，说明顺序表中没有元素存在

	return seq;
}

//判空
int seqlist_is_empty(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last == -1)?1:0);
}

//判满
int seqlist_is_full(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return ((seq->last+1 == SIZE)?1:0);
}

//求表长
int seqlist_length(seqlist *seq)
{
	if(seq == NULL)
		return -1;
	return (seq->last+1);
}

//插入：按位置插入数据元素
int inserSeqlistByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)			//malloc是否成功
		return -1;

	if(seqlist_is_full(seq) == 1)	//判满
		return -1;

	int len = seqlist_length(seq);	//插入的位置
	if(pos < 0 || pos > len)
		return -1;

	int i = 0;
	for(i= seq->last; i>=pos; i--)
	{
		seq->data[i+1] = seq->data[i];
	}
	seq->data[pos] = data;
	seq->last++;
}

//插入：按位置插入数据元素
int deleteSeqlistByPos(seqlist *seq, int pos)
{
	if(NULL == seq)
		return -1;

	if(seqlist_is_empty(seq) == 1)	//判空
		return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	int i = 0;

	for(i=pos; i<seq->last; i++)
	{
		seq->data[i] = seq->data[i+1];
	}
	seq->last--;
}

//查找：按位置来查找数据元素
data_t findSeqlistByPos(seqlist * seq, int pos)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;

	return seq->data[pos];
}

//修改：按位置来修改数据元素
int changSeqlisByPos(seqlist *seq, int pos, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
	return -1;

	int len = seqlist_length(seq);
	if(pos < 0 || pos > seq->last)
		return -1;
	
	seq->data[pos] = data;	//按位置来修改数据元素
}

//查找：按值来查找数据元素,返回那个值的下标
int findSeqlistByData(seqlist *seq, data_t data)
{
	if(NULL == seq)
		return -1;
	if(seqlist_is_empty(seq) == 1)
		return -1;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		if(seq->data[i] == data)
		{
			return i;
		}
	}
}

//删除：按值来删除数据元素
int deleteSeqlistByData(seqlist *seq, data_t data)
{
	int pos = findSeqlistByData(seq, data);

	deleteSeqlistByPos(seq, pos);
}

//修改：按值来修改数据元素
int changeSeqlistByData(seqlist *seq, data_t old_data, data_t new_data)
{
	int pos = findSeqlistByData(seq, old_data);

	changSeqlisByPos(seq, pos, new_data);
}

//清空
void clearSeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	seq->last = -1;
}

//销毁：把地址的地址回收掉
void destroySeqlist(seqlist **seq)
{
	free(*seq);

	*seq = NULL;
}

//输出
void displaySeqlist(seqlist *seq)
{
	if(NULL == seq)
		return;

	if(seqlist_is_empty(seq) == 1)
		return ;
	
	int i = 0;
	for(i=0; i<=seq->last; i++)
	{
		printf("%d ", seq->data[i]);
	}

	puts(" ");
}
						
						

main.c

#include 
#include 
#include 
#include 

#include "seqlist.h"

int main(int argc, const char *argv[])
{
	seqlist *seq = creatSeqlist();
	if(seq == NULL)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = seqlist_is_empty(seq);
	printf("line:%d, n:%d\n",__LINE__, n);

	int m = seqlist_is_full(seq);
	printf("line:%d, n:%d\n",__LINE__, m);

	int len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);

	//按位置插入数据元素
	int i = 0;
	while(i<10)
	{
		inserSeqlistByPos(seq, i, i+1);
		i++;
	}
	len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);
	//打印输出
	displaySeqlist(seq);

	//按位置删除
	deleteSeqlistByPos(seq, 2);
	//打印输出
	displaySeqlist(seq);

	//按位置来查找数据元素
	data_t data = findSeqlistByPos(seq, 5);
	printf("data = %d\n", data);

	//按位置来修改数据元素
	changSeqlisByPos(seq, 1, 250);
	//打印yy输出
	displaySeqlist(seq);

	//查找：按值来查找数据元素,返回那个值的下标
	int pos = findSeqlistByData(seq, 250);
	printf("line:%d, pos = %d\n", __LINE__, pos);

	//删除：按值来删除数据元素
	deleteSeqlistByData(seq, 7);
	displaySeqlist(seq);

	//修改：按值来修改数据元素
	changeSeqlistByData(seq, 10, 100);
	displaySeqlist(seq);

	//清空
	clearSeqlist(seq);
	displaySeqlist(seq);
	len = seqlist_length(seq);
	printf("line:%d, n:%d\n",__LINE__, len);

	//销毁
	destroySeqlist(&seq);
	printf("seq = %p\n", seq);

	return 0;										

2.3、链表

转载 数据结构：链表 参考链接：https://www.jianshu.com/p/73d56c3d228c

2.3.1、线性表
顺序表
链表

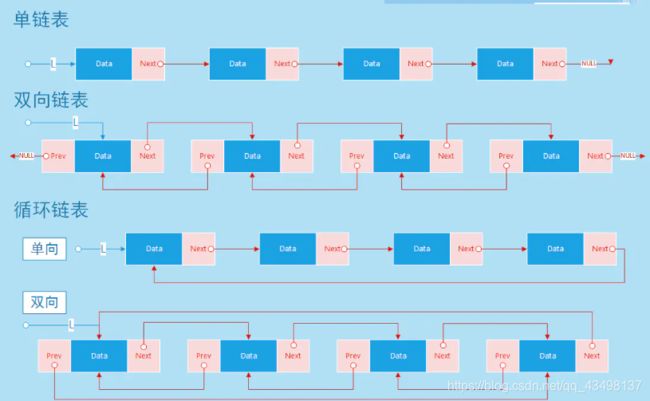
2.3.2、链表（练式存储）：单链表、双链表、循环链表、双向循环链表

2.3.3、单链表
(1)用链表存储实现的线性结构

(2)一个结点存储一个数据元素

(3)各结点之间先后关系用一个指针表示

2.3.4、单链表基本运算
初始化-创建
判空
求链表节点个数
按位置添加节点
按位置删除节点
按位置查找节点
按位置修改节点
打印链表
清空链表
销毁链表

按值查找节点
按值删除节点
按值修改节点
链表逆序

2.3.5、单链表的实现
(1)、linklist.c

#include 
#include 
#include 

typedef int data_t;

//链表
typedef struct node{
	data_t data; //数据域
	struct node *next; //指针域 ： 保存下一个结点的地址
}linklist;

//初始化：链表
linklist *createLinklist()
{
	linklist *head = (linklist *)malloc(sizeof(linklist));
	if(NULL == head)
		return NULL;

	//head->data = -1;
	head->next = NULL;

	return ;
}

//判空
int linklist_is_empty(linklist *head)
{
	if(NULL == head)
		return -1;

	return ((head->next == NULL)?1:0);
}

//求链表的有效结点的个数
int linklist_length(linklist *head)
{
	if(NULL == head)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while( p != NULL)
	{
		num++;
		p = p->next;
	}
	return num;
}

//插入： 按位置添加结点
int insertLinklistByPos(linklist *head, int pos, data_t data)
{
	if(NULL == head)
		return -1;

	int len = linklist_length(head);

	if(pos < 0 || pos > len)
		return -1;

	//初始化一个new结点
	linklist *new = (linklist *)malloc(sizeof(linklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->next = NULL;

	//找到pos的上一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//把新的new结点，连线，先连后断
	new->next = p->next;
	p->next = new;
}

//删除： 按位置删除结点
int deleteLinklistByPos(linklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	//首先找到pos的前一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//连线
	linklist *q = p->next;
	p->next = q->next;

	//把结点回收掉
	free(q);
	q = NULL;
}

//查找: 按位置查找结点
data_t findLinklistByPos(linklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	linklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	return p->data;
}

//修改: 按位置修改结点
int changeLinklistByPos(linklist *head, int pos , data_t data)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	linklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	p->data = data;
}

//查找： 按值查找,返回要找的值所在的结点的下标
int findLinklistByData(linklist *head, data_t data)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while(p != NULL)
	{
		if(p->data == data)
		{
			break;
		}
		else{
			num++;
			p = p->next;
		}
	}

	return num;
}

//删除： 按值删除
int deleteLinklistByData(linklist *head, data_t data)
{
	int pos = findLinklistByData(head, data);
	deleteLinklistByPos(head, pos);
}

//修改： 按值修改
int changeLinklistByData(linklist *head, data_t old, data_t new)
{
	int pos = findLinklistByData(head, old);
	changeLinklistByPos(head, pos, new);
}


//逆序： 头插法
int linklistNixu(linklist *head)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	linklist *p = head->next;

	linklist *q = NULL;

	head->next = NULL;

	while( p != NULL)
	{
		q = p->next;

		p->next = head->next;
		
		head->next = p;
		
		p = q;
	}
}

//遍历链表，打印结点的数据域的值
int displayLinklist(linklist *head)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	linklist *p = head->next; 

	while(p != NULL)
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

//清空链表
void clearLinklist(linklist *head)
{
	if(NULL == head)
		return ;

	if(linklist_is_empty(head) == 1)
		return ;

	linklist *p = head->next;

	head->next = NULL;

	linklist *q = NULL;

	while(p != NULL)
	{
		q = p->next;
	
		free(p);
		p = q;
	}
}

//销毁链表
void destroyLinklist(linklist **head)
{
	clearLinklist(*head);
	
	free(*head);

	*head = NULL;
}

int main(int argc, const char *argv[])
{
	linklist *head = createLinklist();
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = linklist_is_empty(head);
	printf("line:%d n=%d\n", __LINE__, n);

	int m = linklist_length(head);
	printf("line:%d m=%d\n", __LINE__, m);

	//按位置

	int i = 0;
	while(i<10)
	{
		insertLinklistByPos(head, i, i+1);
		i++;
	}

	int len = linklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);

	displayLinklist(head);

	deleteLinklistByPos(head, 5);
	displayLinklist(head);

	data_t data = findLinklistByPos(head, 1);
	printf("line:%d data= %d\n", __LINE__, data);	

	changeLinklistByPos(head, 7, 666);
	displayLinklist(head);


	//按值：查找、删除、修改
	int pos = findLinklistByData(head, 7);
	printf("line:%d pos= %d\n", __LINE__, pos);	
	
	deleteLinklistByData(head, 4);
	displayLinklist(head);
	
	changeLinklistByData(head, 666, 999);
	displayLinklist(head);

	//链表逆序
	linklistNixu(head);
	displayLinklist(head);


	clearLinklist(head);
	displayLinklist(head);

	destroyLinklist(&head);
	printf("%p\n", head);

	return 0;
}
					
					

(2)、模块化编程
linklist.h

#ifndef _LINKLIST_H
#define _LINKLIST_H

#include 
#include 
#include 

typedef int data_t;			//重命名int

//链表
typedef struct node{

	data_t data;			//数据域	
	struct node *next;		//指针域：保存下一个结点的地址
}linklist;

linklist *createLinklist();										//初始化：链表
int linklist_is_empty(linklist *head);							//判空
int linklist_length(linklist *head);							//求链表的有效结点数
int insertLinklistByPos(linklist *head, int pos, data_t data);	//插入：按位置添加结点
int deleteLinklistByPos(linklist *head, int pos);				//删除：按位置删除结点
int findLinklistByPos(linklist *head, int pos);					//查找：按位置查找结点
int changeListByPos(linklist *head, int pos, data_t data);		//修改：按位置修改结点

int findLinklistByData(linklist *head, data_t data);			//查找：按值查找，返回要找的值所在的结点的下标
int deletLinklistByData(linklist *head, data_t data);			//删除：按值删除
int changLinklistByData(linklist *head, data_t old, data_t new);//修改：按值修改

int linklistNixu(linklist *head);		//链表逆序：头插法
int displayLinklist(linklist *head);	//遍历链表：打印结点的数据域的值
void clearLinklist(linklist *head);		//清空链表
void destroyLinklist(linklist **head);	//销毁链表

#endif												

linklist.c

#include 
#include 
#include 
#include 

#include "linklist.h"

linklist *createLinklist()					//初始化：链表
{
	linklist *head = (linklist *)malloc(sizeof(linklist));
	if(NULL == head)
		return NULL;

	head->next = NULL;

	return head;
}

int linklist_is_empty(linklist *head)				//判空
{
	if(NULL == head)
		return -1;

	return ((head->next == NULL)?1:0);
}

int linklist_length(linklist *head)				//请链表的有效结点数
{
	if (NULL == head)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while(p != NULL)
	{
		num++;
		p = p->next;
	}
	return num;
}

int insertLinklistByPos(linklist *head, int pos, data_t data)	//插入：按位置添加结点
{
	if(NULL == head)
		return -1;

	int len = linklist_length(head);

	if(pos < 0 || pos > len)
		return -1;

	//初始化一个new结点
	linklist *new = (linklist *)malloc(sizeof(linklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->next = NULL;

	//找到pos的上一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//把新的new结点，连线，先连后断
	new->next = p->next;
	p->next = new;
}

int deleteLinklistByPos(linklist *head, int pos)		//删除：按位置删除结点
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);
	if(pos<0 || pos>len-1)
		return -1;

	//首先找到pos的前一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//连线
	linklist *q = p->next;
	p->next = q->next;

	//把结点收回掉
	free(q);
	q = NULL;
}

int findLinklistByPos(linklist *head, int pos)			//查找：按位置查找结点
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);
	if(pos<0 || pos>len-1)
		return -1;

	linklist *p = head->next;				//第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	return p->data;
}

int changeListByPos(linklist *head, int pos, data_t data)	//修改：按位置修改结点
{
	if(NULL == head)
		return -1;
	
	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);
	if(pos<0 || pos > len-1)
		return -1;

	linklist *p = head->next;				//第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	p->data = data;
}

int findLinklistByData(linklist *head, data_t data)		//查找：按值查找，返回要找的值所在的结点的下标
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while(p != NULL)
	{
		if(p->data == data)
		{
			break;
		}
		else
		{
			num++;
			p = p->next;
		}
	}
	return num;
}

int deletLinklistByData(linklist *head, data_t data)		//删除：按值删除
{
	int pos = findLinklistByData(head, data);
	deleteLinklistByPos(head, pos);
}

int changLinklistByData(linklist *head, data_t old, data_t new) //修改：按值修改
{
	int pos = findLinklistByData(head, old);
	changeListByPos(head, pos, new);
}

int linklistNixu(linklist *head)				//链表逆序：头插法
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;
	
	linklist *p = head->next;

	linklist *q = NULL;

	head->next = NULL;

	while(p != NULL)
	{
		q = p->next;

		p->next = head->next;

		head->next = p;

		p = q;
	}
}

int displayLinklist(linklist *head)				//遍历链表：打印结点的数据域的值
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	linklist *p = head->next;

	while(p != NULL)
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

void clearLinklist(linklist *head)				//清空链表
{
	if(NULL == head)
		return ;

	if(linklist_is_empty(head) == 1)
		return ;

	linklist *p = head->next;

	head->next = NULL;

	linklist *q = NULL;

	while(p != NULL)
	{
		q = p->next;

		free(p);
		p = q;
	}
}

void destroyLinklist(linklist **head)				//销毁链表
{
	clearLinklist(*head);

	free(*head);

	*head = NULL;
}
						
						

main.c

#include 
#include 
#include 
#include 

#include "linklist.h"

int main(int argc, char *argv[])
{
	linklist *head = createLinklist();			//初始化链表
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = linklist_is_empty(head);			//判空
	printf("line:%d, n=%d\n", __LINE__, n);		//：
	
	int m = linklist_length(head);				//链表有效结点数
	printf("line:%d, m=%d\n", __LINE__, m);		//：

	//按位置：增、删、改、查
	int i = 0;
	while(i < 10)
	{
		insertLinklistByPos(head, i, i+1);		//按位置插入
		i++;
	}

	int len = linklist_length(head);			//链表有效结点数
	printf("line:%d, len=%d\n", __LINE__, len);	//：   

	displayLinklist(head);						//：   

	deleteLinklistByPos(head, 1);				//按位置删除
	displayLinklist(head);						//：   	

	data_t data = findLinklistByPos(head, 1);	//按位置查找
	printf("line:%d, data=%d\n", __LINE__, data);	//：   

	changeListByPos(head, 7, 666);				//按位置修改
	displayLinklist(head);						//：   
	
	//按值：增、删、改、查
	int pos = findLinklistByData(head, 7);		//按值查找
	printf("line:%d, pos=%d\n", __LINE__, pos);	//：   

	deletLinklistByData(head, 4);				//按值来删
	displayLinklist(head);						//：   

	changLinklistByData(head, 666, 999);		//按值来改
	displayLinklist(head);						//：   

	linklistNixu(head);							//链表逆序
	displayLinklist(head);						//：   

	clearLinklist(head);						//清空链表
	displayLinklist(head);						//：   

	destroyLinklist(&head);						//销毁链表
	printf("%p\n",head);						//：   

	return 0;
}					

输出结果：

line:29, n=1
line:32, m=0
line:43, len=10
1 2 3 4 5 6 7 8 9 10 
1 3 4 5 6 7 8 9 10 
line:51, data=3
1 3 4 5 6 7 8 666 10 
line:58, pos=5
1 3 5 6 7 8 666 10 
1 3 5 6 7 8 999 10 
10 999 8 7 6 5 3 1 
(nil)

2.4、顺序表 vs 链表

2.4.1、顺序表

• (1)支持随机访问。
• (2)存储密度高。
• (3)大片连续空间分配不方便，改变容量不方便。
• (4)插入或删除元素要将后续元素都后移或前移。

2.4.2、链表

• (1)不支持随机访问。
• (2)存储密度低。
• (3)离散的小空间分配方便，改变容量方便。
• (4)插入或删除元素只需修改指针即可。

2.4.3、

• (1)在查询操作使用的比较频繁时，使用顺序表会好一些；
• (2)在插入、删除操作使用的比较频繁时，使用单链表会好一些。

2.5、双链表

双链表的实现

#include 
#include 
#include 

typedef int data_t;

typedef struct node{
	data_t data; //数据域
	struct node *next; //下一个结点的地址
	struct node *prior; //上一个结点的地址
}dlinklist;

//创建
dlinklist *createDlinklist()
{
	dlinklist *head = (dlinklist *)malloc(sizeof(dlinklist));
	if(NULL == head)
		return NULL;

	head->next = NULL;
	head->prior = NULL;

	return head;
}

//判空
int dlinklist_is_empty(dlinklist *head)
{
	if(NULL == head)
		return -1;

	return ((head->next == head->prior)?1:0);
}

//求表长
int dlinklist_length(dlinklist *head)
{
	if(NULL == head)
		return -1;

	dlinklist *p = head->next;

	int num = 0;
	while(p != NULL)
	{
		num++;
		p = p->next;
	}
	return num;
}


//按位置插入
int insertDlinklistByPos(dlinklist *head, int pos, data_t data)
{
	if(NULL == head)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0 || pos > len)
		return -1;

	//new一个新的结点
	dlinklist *new = (dlinklist *)malloc(sizeof(dlinklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->prior = NULL;
	new->next = NULL;

	//找到pos的上一个结点
	dlinklist *p = head;
	while(pos--)
		p = p->next;

	if(p->next != NULL)  //在中间位置插入
	{
		new->next = p->next;
		new->prior = p;

		p->next = new;
		new->next->prior = new;
	}
	else{  //在末尾位置插入
	
		p->next = new;
		new->prior = p;
	}

}

//按位置删除
int deleteDlinklistByPos(dlinklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;
	
	int len = dlinklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	dlinklist *p = head;
	while(pos--)
		p = p->next;

	dlinklist *q = p->next;


	if(q->next != NULL) //在中间位置删除
	{
		p->next = q->next;

		q->next->prior = p;

		：:(q);
		q = NULL;
	
	}
	else{ //在末尾位置删除
	
		p->next = NULL;
		free(q);
		q = NULL;
	}

}

//按位置查找
//按位置修改
//查找: 按位置查找结点
data_t findDlinklistByPos(dlinklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	dlinklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	return p->data;
}

//修改: 按位置修改结点
int changeDlinklistByPos(dlinklist *head, int pos , data_t data)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0 || pos > len-1)
		return -1;

	dlinklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	p->data = data;
}

//打印
void displayDlinklist(dlinklist *head)
{
	if(NULL == head)
		return;

	dlinklist *p = head->next; 

	while( p != NULL)
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

//清空
//销毁
//清空链表
void clearDlinklist(dlinklist *head)
{
	if(NULL == head)
		return ;

	dlinklist *p = head->next;

	head->next = NULL;

	dlinklist *q = NULL;

	while(p != NULL)
	{
		q = p->next;
	
		free(p);
		p = q;
	}
}

//销毁链表
void destroyDlinklist(dlinklist **head)
{
	clearDlinklist(*head);
	
	free(*head);

	*head = NULL;
}

int main(int argc, const char *argv[])
{
	dlinklist *head = createDlinklist();
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = dlinklist_is_empty(head);
	printf("line:%d n=%d\n", __LINE__, n);

	int len = dlinklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);	

	int i = 0;
	while(i<10)
	{
		insertDlinklistByPos(head, i, i+1);
		i++;
	}

	len = dlinklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);	

	displayDlinklist(head);


	deleteDlinklistByPos(head, 5);
	displayDlinklist(head);

	//查找
	data_t data = findDlinklistByPos(head, 3);
	printf("line:%d data=%d\n", __LINE__, data);

	//修改
	changeDlinklistByPos(head, 8, 80);
	displayDlinklist(head);

	//清空
	clearDlinklist(head);
	displayDlinklist(head);

	destroyDlinklist(&head);
	printf("%p\n", head);

	return 0;
}										

2.6、循环链表

2.6.1、单项循环链表的实现

#include 
#include 
#include 

typedef int data_t;

//链表
typedef struct node{
	data_t data; //数据域
	struct node *next; //指针域 ： 保存下一个结点的地址
}linklist;

//初始化：链表
linklist *createLinklist()
{
	linklist *head = (linklist *)malloc(sizeof(linklist));
	if(NULL == head)
		return NULL;

	//head->data = -1;
	head->next = head; //111111111111111111111111111111111111111

	return head;
}

//判空
int linklist_is_empty(linklist *head)
{
	if(NULL == head)
		return -1;

	return ((head->next == head)?1:0);  //2222222222222222222222222222222
}

//求链表的有效结点的个数
int linklist_length(linklist *head)
{
	if(NULL == head)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while( p != head)  //33333333333333333333333333333333
	{
		num++;
		p = p->next;
	}
	return num;
}

//插入： 按位置添加结点
int insertLinklistByPos(linklist *head, int pos, data_t data)
{
	if(NULL == head)
		return -1;

	int len = linklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%(len+1); //44444444444444444444444444444444

	//初始化一个new结点
	linklist *new = (linklist *)malloc(sizeof(linklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->next = NULL;

	//找到pos的上一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//把新的new结点，连线，先连后断
	new->next = p->next;
	p->next = new;
}

//删除： 按位置删除结点
int deleteLinklistByPos(linklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len; //555555555555555555555555555

	//首先找到pos的前一个结点
	linklist *p = head;
	while(pos--)
	{
		p = p->next;
	}

	//连线
	linklist *q = p->next;
	p->next = q->next;

	//把结点回收掉
	free(q);
	q = NULL;
}

//查找: 按位置查找结点
data_t findLinklistByPos(linklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len; //66666666666666666666666666666666

	linklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	return p->data;
}

//修改: 按位置修改结点
int changeLinklistByPos(linklist *head, int pos , data_t data)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int len = linklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len; //777777777777777777777777777777777

	linklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	p->data = data;
}

//查找： 按值查找,返回要找的值所在的结点的下标
int findLinklistByData(linklist *head, data_t data)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	int num = 0;
	linklist *p = head->next;
	while(p != head) //88888888888888888888888888888
	{
		if(p->data == data)
		{
			break;
		}
		else{
			num++;
			p = p->next;
		}
	}

	return num;
}

//删除： 按值删除
int deleteLinklistByData(linklist *head, data_t data)
{
	int pos = findLinklistByData(head, data);
	deleteLinklistByPos(head, pos);
}

//修改： 按值修改
int changeLinklistByData(linklist *head, data_t old, data_t new)
{
	int pos = findLinklistByData(head, old);
	changeLinklistByPos(head, pos, new);
}


//链表逆序： 头插法
int linklistNixu(linklist *head)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	linklist *p = head->next;

	linklist *q = NULL;

	head->next = head; //*****************************

	while( p != head) //9999999999999999999999999999999
	{
		q = p->next;

		p->next = head->next;
		
		head->next = p;
		
		p = q;
	}
}

//遍历链表，打印结点的数据域的值
int displayLinklist(linklist *head)
{
	if(NULL == head)
		return -1;

	if(linklist_is_empty(head) == 1)
		return -1;

	linklist *p = head->next; 

	while(p != head) //10 10 10 10 10 10 10 10 10 10
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

//清空链表
void clearLinklist(linklist *head)
{
	if(NULL == head)
		return ;

	if(linklist_is_empty(head) == 1)
		return ;

	linklist *p = head->next;

	head->next = head; //****************************

	linklist *q = NULL;

	while(p != head) // 11 11 11 11 11 11 11 11 11 11
	{
		q = p->next;
	
		free(p);
		p = q;
	}
}

//销毁链表
void destroyLinklist(linklist **head)
{
	clearLinklist(*head);
	
	free(*head);

	*head = NULL;
}

int main(int argc, const char *argv[])
{
	linklist *head = createLinklist();
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = linklist_is_empty(head);
	printf("line:%d n=%d\n", __LINE__, n);

	int m = linklist_length(head);
	printf("line:%d m=%d\n", __LINE__, m);

	//按位置
	int i = 0;
	while(i<3)
	{
		insertLinklistByPos(head, i, i+1);
		i++;
	}

	int len = linklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);

	//2 6 10
	insertLinklistByPos(head,10,4);
	displayLinklist(head);

/*
	displayLinklist(head);

	deleteLinklistByPos(head, 5);
	displayLinklist(head);

	data_t data = findLinklistByPos(head, 1);
	printf("line:%d data= %d\n", __LINE__, data);	

	changeLinklistByPos(head, 7, 666);
	displayLinklist(head);


	//按值：查找、删除、修改
	int pos = findLinklistByData(head, 7);
	printf("line:%d pos= %d\n", __LINE__, pos);	
	
	deleteLinklistByData(head, 4);
	displayLinklist(head);
	
	changeLinklistByData(head, 666, 999);
	displayLinklist(head);

	//链表逆序
	linklistNixu(head);
	displayLinklist(head);


	clearLinklist(head);
	displayLinklist(head);

	destroyLinklist(&head);
	printf("%p\n", head);
*/
	return 0;
}	
					
				

2.6.2、双向循环链表的实现

#include 
#include 
#include 

typedef int data_t;

typedef struct node{
	data_t data; //数据域
	struct node *next; //下一个结点的地址
	struct node *prior; //上一个结点的地址
}dlinklist;

//创建
dlinklist *createDlinklist()
{
	dlinklist *head = (dlinklist *)malloc(sizeof(dlinklist));
	if(NULL == head)
		return NULL;

	head->next = head;    //11111111111111111111111111
	head->prior = head;

	return head;
}

//判空
int dlinklist_is_empty(dlinklist *head)
{
	if(NULL == head)
		return -1;

	return ((head->next == head->prior)?1:0);
}

//求表长
int dlinklist_length(dlinklist *head)
{
	if(NULL == head)
		return -1;

	dlinklist *p = head->next;

	int num = 0;
	while(p != head)  //222222222222222222222222222
	{
		num++;
		p = p->next;
	}
	return num;
}

//按位置插入
int insertDlinklistByPos(dlinklist *head, int pos, data_t data)
{
	if(NULL == head)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%(len+1); //33333333333333333333333333333333

	//new一个新的结点
	dlinklist *new = (dlinklist *)malloc(sizeof(dlinklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->prior = NULL;
	new->next = NULL;

	//找到pos的上一个结点
	dlinklist *p = head;
	while(pos--)
		p = p->next;

	new->next = p->next;
	new->prior = p;

	p->next = new;
	new->next->prior = new;
}

//按位置删除
int deleteDlinklistByPos(dlinklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;
	
	int len = dlinklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len; //44444444444444444444444444444444444444

	dlinklist *p = head;
	while(pos--)
		p = p->next;

	dlinklist *q = p->next;

	p->next = q->next;

	q->next->prior = p;

	free(q);
	q = NULL;							
}

//按位置查找
//按位置修改
//查找: 按位置查找结点
data_t findDlinklistByPos(dlinklist *head, int pos)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len;//55555555555555555555555555555555

	dlinklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	return p->data;
}

//修改: 按位置修改结点
int changeDlinklistByPos(dlinklist *head, int pos , data_t data)
{
	if(NULL == head)
		return -1;

	if(dlinklist_is_empty(head) == 1)
		return -1;

	int len = dlinklist_length(head);

	if(pos < 0)
		return -1;

	pos = pos%len;//666666666666666666666666666666666666666

	dlinklist *p = head->next; //第一个有效结点
	while(pos--)
	{
		p = p->next;
	}

	p->data = data;
}

//打印
void displayDlinklist(dlinklist *head)
{
	if(NULL == head)
		return;

	dlinklist *p = head->next; 

	while( p != head)  //7777777777777777777777777
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

//清空
//销毁
//清空链表
void clearDlinklist(dlinklist *head)
{
	if(NULL == head)
		return ;

	dlinklist *p = head->next;

	head->next = head; //8888888888888888888

	dlinklist *q = NULL;

	while(p != head) //99999999999999999999999
	{
		q = p->next;
	
		free(p);
		p = q;
	}
}

//销毁链表
void destroyDlinklist(dlinklist **head)
{
	clearDlinklist(*head);
	
	free(*head);

	*head = NULL;
}

int main(int argc, const char *argv[])
{
	dlinklist *head = createDlinklist();
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = dlinklist_is_empty(head);
	printf("line:%d n=%d\n", __LINE__, n);

	int len = dlinklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);	

	int i = 0;
	while(i<3)
	{
		insertDlinklistByPos(head, i, i+1);
		i++;
	}

	len = dlinklist_length(head);
	printf("line:%d len=%d\n", __LINE__, len);	

	//2 6 10
	insertDlinklistByPos(head,10,4);
	displayDlinklist(head);


/*
	displayDlinklist(head);


	deleteDlinklistByPos(head, 5);
	displayDlinklist(head);

	//查找
	data_t data = findDlinklistByPos(head, 3);
	printf("line:%d data=%d\n", __LINE__, data);

	//修改
	changeDlinklistByPos(head, 8, 80);
	displayDlinklist(head);

	//清空
	clearDlinklist(head);
	displayDlinklist(head);

	destroyDlinklist(&head);
	printf("%p\n", head);
*/
	return 0;
}													

三、栈 stack

栈（Stack）是一种线性数据结构但是在存取数据的方式上还是不太一样，栈是一种先进后出的一种数据结构。

栈的插入和删除操作只允许在表的一端进行，这个可以操作的端就叫做栈顶，而另一端被称为栈底。

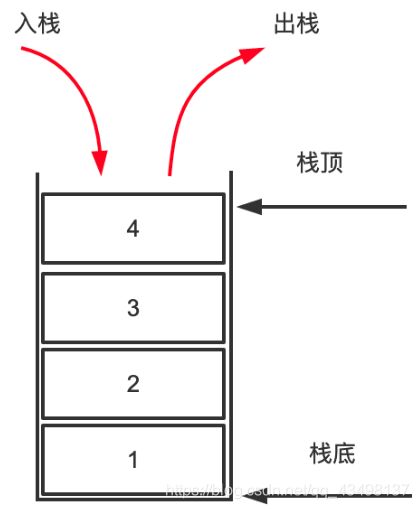
3.1、栈的概念及特点

栈是限制在一端进行插入操作和删除操作的线性表。

允许进行操作的一端称为“栈顶”，
另一固定端称为“栈底”，
当栈中没有元素时称为“空栈”。

特点： 先进后出、后进先出

3.2、顺序栈

3.2.1、基本运算：
创建
判空
判满
求长度
入栈
出栈
打印
清空
销毁

3.2.2、顺序栈的实现：

#include 
#include 
#include 

#define SIZE 100

typedef int data_t;

typedef struct list{
	data_t data[SIZE];
	int top;  //栈顶的下标
}seqstack;

//栈的初始化
seqstack *createSeqstack()
{
	seqstack *s = (seqstack *)malloc(sizeof(seqstack));
	if(NULL == s)
		return NULL;

	memset(s->data, 0, sizeof(s->data));

	s->top = -1;
	
	return s;
}

//栈空
int seqstack_is_empty(seqstack *s)
{
	if(NULL == s)
		return -1;

	return ( (s->top == -1)?1:0 );
}

//栈满
int seqstack_is_full(seqstack *s)
{
	if(NULL == s)
		return -1;

	return ( (s->top+1 == SIZE)?1:0 );
}

//栈长度
int seqstack_length(seqstack *s)
{
	if(NULL == s)
		return -1;

	return s->top+1;
}

//入栈
int seqstack_in(seqstack *s, data_t data)
{
	if(NULL == s)
		return -1;

	if(seqstack_is_full(s) == 1)
		return -1;
	
	s->data[s->top+1] = data;

	s->top++;
}

//出栈
data_t seqstack_out(seqstack *s)
{
	if(NULL == s)
		return -1;

	if(seqstack_is_empty(s) == 1)
		return -1;

	data_t data = s->data[s->top];

	s->top--;

	return data;
}

//打印
void displaySeqstack(seqstack *s)
{
	if(NULL == s)
		return ;

	if(seqstack_is_empty(s) == 1)
		return ;

	int i;
	for(i=s->top; i>=0; i--)
	{
		printf("%d ", s->data[i]);
	}

	puts("");
}

//清空
void clearSeqstack(seqstack *s)
{
	s->top = -1;
}

int main(int argc, const char *argv[])
{
	seqstack *s = createSeqstack();	
	if(NULL == s)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = seqstack_is_empty(s);
	printf("line:%d n = %d\n", __LINE__, n);

	int m = seqstack_is_full(s);
	printf("line:%d m = %d\n", __LINE__, m);

	int len = seqstack_length(s);
	printf("line:%d len = %d\n", __LINE__, len);

	//入栈
	int i = 0;
	while(i<10)
	{
		seqstack_in(s, i+1);
		i++;
	}

	len = seqstack_length(s);
	printf("line:%d len = %d\n", __LINE__, len);

	displaySeqstack(s);

	
	//出栈
	i=0;
	while(i<5)
	{
		data_t data = seqstack_out(s);
		printf("data:%d ", data);
		i++;
	}

	puts("");

	displaySeqstack(s);

	clearSeqstack(s);
	displaySeqstack(s);

	return 0;
}							

3.3、链式栈

3.3.1、基本运算：
创建
判空
求长度
入栈   //头插法，只能在头插
出栈
打印
清空
销毁

3.3.2、链式栈的实现：

#include 
#include 
#include 

typedef int data_t;

typedef struct stack{
	data_t data;
	struct stack *next;
}linkstack;

//栈的初始化
linkstack *createLinkstack()
{
	linkstack *head = (linkstack *)malloc(sizeof(linkstack));
	if(NULL == head)
		return NULL;

	head->next = NULL;

	return head;
}

//栈的判空
int linkstack_is_empty(linkstack *head)
{
	if(NULL == head)
		return -1;

	return ( ( head->next == NULL)?1:0 );
}

//栈的长度
int linkstack_length(linkstack *head)
{
	if(NULL == head)
		return -1;

	linkstack *p = head->next;

	int num = 0;
	while(p != NULL)
	{
		num++;
		p = p->next;
	}
	return num;
}

//入栈
int linkstack_in(linkstack *head, data_t data)
{
	if(NULL == head)
		return -1;
	
	linkstack *new = (linkstack *)malloc(sizeof(linkstack));
	if(NULL == new)
		return -1;

	new->data = data;
	new->next = NULL;

	//插入
	new->next = head->next;

	head->next = new;
}

//出栈
data_t linkstack_out(linkstack *head)
{
	if(NULL == head)
		return -1;
	
	if(linkstack_is_empty(head) == 1)
		return -1;

	linkstack *p = head->next;

	data_t data = p->data;

	head->next = p->next;

	free(p);

	p = NULL;

	return data;
}

//打印
void displayLinkstack(linkstack *head)
{
	if(NULL == head)
		return;

	linkstack *p = head->next;

	while(p != NULL)
	{
		printf("%d ", p->data);

		p = p->next;
	}

	puts("");
}

int main(int argc, const char *argv[])
{
	linkstack *head = createLinkstack();
	if(NULL == head)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = linkstack_is_empty(head);
	printf("line:%d n = %d\n", __LINE__, n);


	int len = linkstack_length(head);
	printf("line:%d len = %d\n", __LINE__, len);
	
	//入栈
	int i = 0;
	while(i<10)
	{
		linkstack_in(head, i+1);
		i++;
	}
	
	displayLinkstack(head);

	//出栈
	i = 0;
	while(i<5)
	{
		data_t data = linkstack_out(head);
		printf("data=%d ", data);
		i++;
	}

	puts("");

	displayLinkstack(head);
	
	return 0;
}			

四、队列 queun

4.1、队列的概念及特点

队列是限制在两端进行插入操作和删除操作的线性表，允许进行存入操作的一端称为“队尾”，允许进行删除操作的一端称为“队头”。当线性表中没有元素时，称为“空队”。

特点：先进先出

规定一：front指向队头元素的位置; rear指向队尾元素的下一个位置。

    或者front指向队头节点的前一个节点; rear指向队尾节点。

规定二：队列的初始化 front = rear = 0;

4.2、顺序队列的基本操作

创建
判空
判满
求长度
入队
出队
打印

顺序队列的实现：

#include 
#include 
#include 

#define SIZE 10

typedef int data_t;

typedef struct{
	data_t data[SIZE];
	int front; //对头元素的位置
	int rear; //队尾元素的下一个位置
}squeue;

//创建
squeue *createSqueue()
{
	squeue *sq = (squeue *)malloc(sizeof(squeue));
	if(NULL == sq)
		return NULL;

	memset(sq->data, 0, sizeof(sq->data));

	sq->front = sq->rear = 0;

	return sq;
}

//判空
int squeue_is_empty(squeue *sq)
{
	if(NULL == sq)
		return -1;

	return ((sq->front == sq->rear)?1:0);
}

//判满
int squeue_is_full(squeue *sq)
{
	if(NULL == sq)
		return -1;

	return (sq->front == (sq->rear+1)%SIZE )?1:0;
}

//求长度
int squeue_length(squeue *sq)
{
	if(NULL == sq)
		return -1;

	int num= 0;
	int temp = sq->front;

	while(temp != sq->rear)
	{
		num++;
	
		temp = (temp+1)%SIZE;
	}

	return num;
}

//入队, 在队尾进行入队操作
int squeue_in(squeue *sq, data_t data)
{
	if(NULL == sq)
		return -1;

	if(squeue_is_full(sq) == 1)
		return -1;

	sq->data[sq->rear] = data;

	sq->rear = (sq->rear+1)%SIZE;
}

//出队
data_t squeue_out(squeue *sq)
{
	if(NULL == sq)
		return -1;

	if(squeue_is_empty(sq) == 1)
		return -1;

	data_t data = sq->data[sq->front];

	sq->front = (sq->front+1)%SIZE;

	return data;
}

//打印
void dispalySqueue(squeue *sq)
{
	if(NULL == sq)
		return;

	int temp = sq->front;

	while(temp != sq->rear)
	{
		printf("%d ", sq->data[temp]);
	
		temp = (temp+1)%SIZE;
	}

	puts("");
}

int main(int argc, const char *argv[])
{
	squeue *sq = createSqueue();
	if(NULL == sq)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int n = squeue_is_empty(sq);
	printf("line:%d n=%d\n", __LINE__, n);

	int m = squeue_is_full(sq);
	printf("line:%d m=%d\n", __LINE__, m);

	int len = squeue_length(sq);
	printf("line:%d len=%d\n", __LINE__, len);
	
	int i= 0;
	while(i<10)
	{
		squeue_in(sq, i+1);
		i++;
	}

	dispalySqueue(sq);

	len = squeue_length(sq);
	printf("line:%d len=%d\n", __LINE__, len);


	i = 0;
	while(i<5)
	{
		data_t data = squeue_out(sq);
		printf("data=%d ", data);
		i++;
	}

	puts("");

	dispalySqueue(sq);
	
	return 0;
}

4.3、链式队列的基本操作

插入操作在队尾进行，删除操作在队头进行，由队头和队尾操控队列操作。

创建
判空
求节点个数
入队
出队
打印

链式队列的实现：

#include 
#include 
#include 

typedef int data_t;

typedef struct node{
	data_t data;
	struct node *next;
}linklist;

typedef struct{
	linklist *front; //指向对头元素的前一个位置
	linklist *rear; //指向队尾元素的位置
}lqueue;

lqueue *createLqueue()
{
	lqueue *lq = (lqueue *)malloc(sizeof(lqueue));
	if(NULL == lq)
		return NULL;

	lq->front = (linklist *)malloc(sizeof(linklist)); //返回头结点的地址
	if(NULL == lq->front)
		return NULL;

	lq->rear = lq->front;

	lq->front->next = NULL;

	return lq;
}

int lqueue_is_empty(lqueue *lq)
{
	if(NULL == lq)
		return -1;

	return (lq->front == lq->rear)?1:0;
}

//求长度
int lqueue_length(lqueue *lq)
{
	if(NULL == lq)
		return -1;

	linklist *p = lq->front->next; //p指向第一个有效结点

	int num = 0;
	while(p != NULL)
	{
		num++;

		p=p->next;
	}
	
	return num;
}

//入队
int lqueue_in(lqueue *lq, data_t data)
{
	if(NULL == lq)
		return -1;

	linklist *new = (linklist *)malloc(sizeof(linklist));
	if(NULL == new)
		return -1;

	new->data = data;
	new->next = NULL;


	lq->rear->next = new; 

	lq->rear = new;

}

//出队
data_t lqueue_out(lqueue *lq)
{
	if(NULL == lq)
		return -1;

	if(lqueue_is_empty(lq))
		return -1;

	linklist *p = lq->front->next; //指向对头元素

	data_t data = p->data;

	lq->front->next = p->next;

	if(lq->front->next == NULL)
		lq->front == lq->rear;

	free(p);
	p = NULL;

	return data;
}

//打印
void displayLqueue(lqueue *lq)
{
	if(NULL == lq)
		return;

	linklist *p = lq->front->next;

	while(p != NULL)
	{
		printf("%d ", p->data);

		p=p->next;
	}

	puts("");
}

int main(int argc, const char *argv[])
{
	lqueue *lq = createLqueue();	
	if(NULL == lq)
	{
		printf("malloc failed!\n");
		return -1;
	}

	int i = 0;
	while(i<10)
	{
		lqueue_in(lq, i+1);
		i++;
	}

	int len = lqueue_length(lq);
	printf("len = %d\n", len);

	displayLqueue(lq);

	i=0;
	while(i<5)
	{
		data_t data = lqueue_out(lq);
		printf("data = %d ", data);
		i++;
	}

	puts("");

	displayLqueue(lq);

	return 0;
}	

五、树

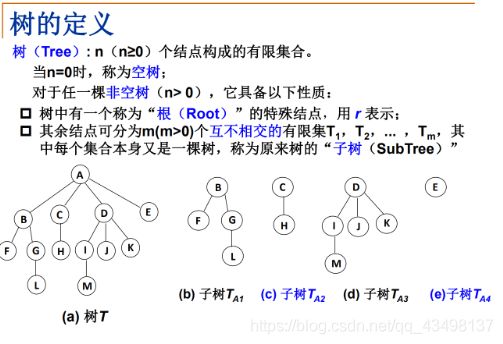
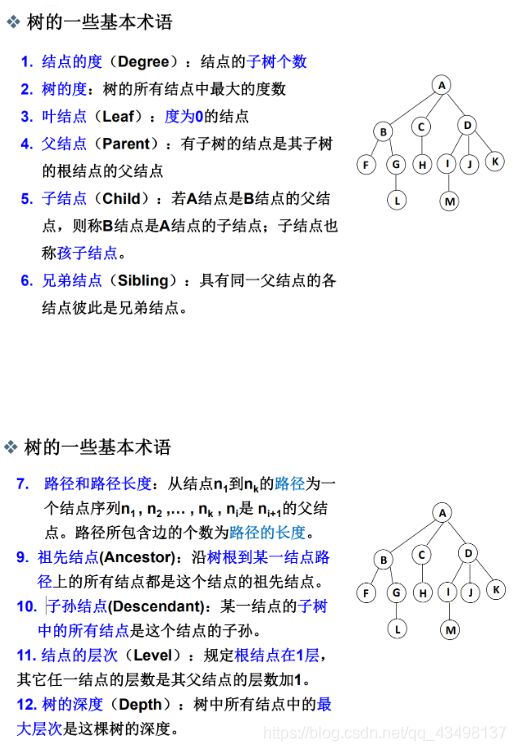
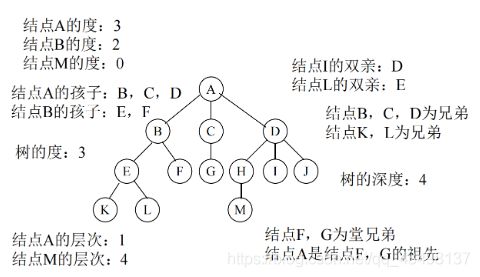
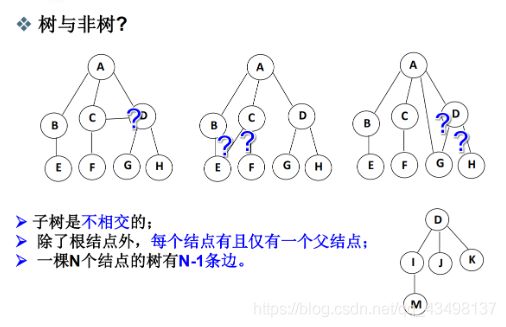
5.1、树的定义

• 有且仅有一个根节点
• 互不相交的有限集合，每一个集合又是一棵树
  
  
  
  

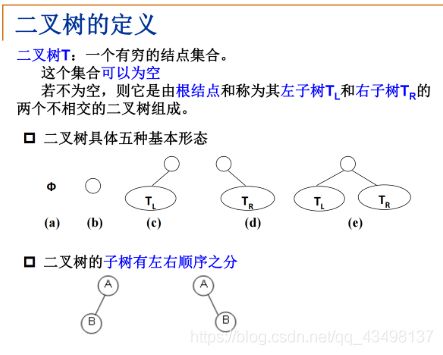
5.2、二叉树

子树 <= 2
二叉树严格区分左孩子和右孩子，即使只有一个字节点也要区分左右。

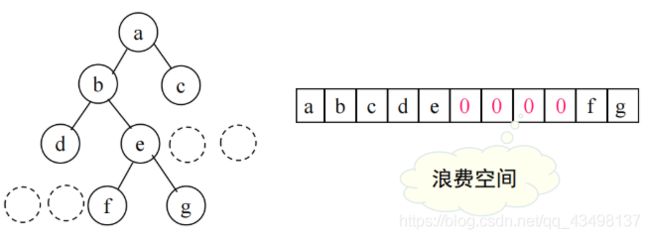
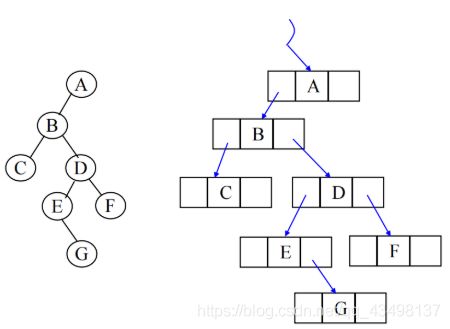
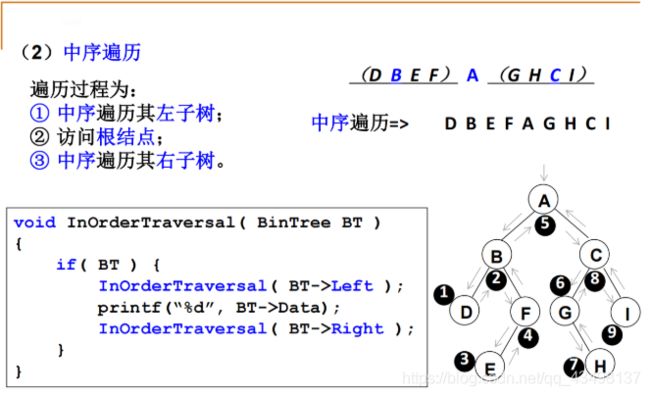
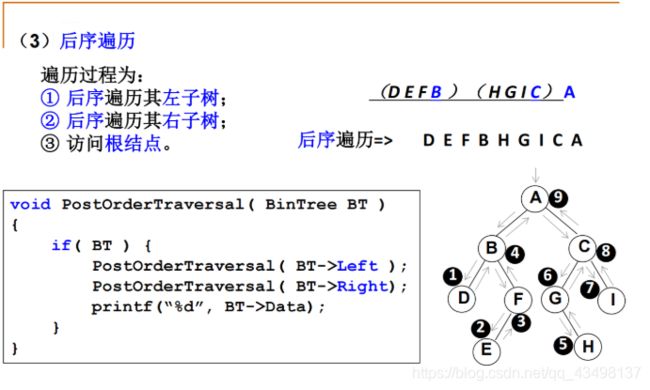
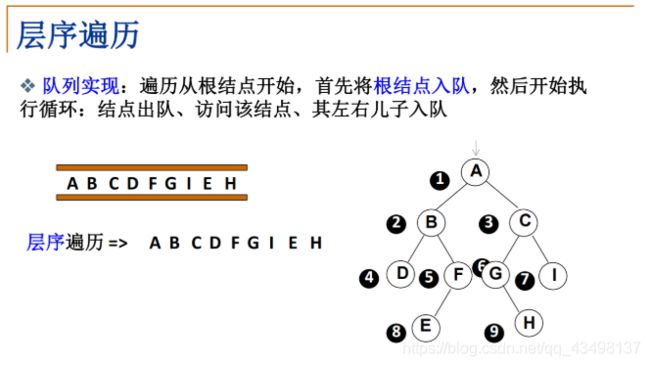
5.3、二叉树遍历

先序：根左右

中序：左根右

后序：左右根


二叉树的实现：

#include 
#include 
#include 

typedef int data_t;

typedef struct node{
	data_t data;
	struct node *lchild;
	struct node *rchild;
}tree;

//创建完全二叉树
//节点个数为：n
//节点编号为: i

tree *createTree(int i, int n)
{
	tree *root = (tree *)malloc(sizeof(tree));
	if(NULL == root)
		return NULL;

	root->data = i;

	if(2*i<=n) //现在有左孩子
	{
		root->lchild = createTree(2*i,n);
	}else
	{
		root->lchild = NULL; //没有左孩子
	}

	if(2*i+1<=n) //现在有右孩子
	{
		root->rchild = createTree(2*i+1, n);
	}else
	{
		root->rchild = NULL; //没有右孩子
	}

	return root;
}

//先序遍历二叉树, 根左右
void dlr(tree *root)
{
	if(NULL == root)
		return;

	printf("%d ", root->data); //根

	dlr(root->lchild);
	dlr(root->rchild);
}

//先序遍历; 根左右
void PreOrderTraversal(tree *root)
{
	if(NULL == root)
		return;
	if(root)
	{
		printf("%d ", root->data);
		PreOrderTraversal(root->lchild);
		PreOrderTraversal(root->rchild);
	}
}

//中序遍历; 左根右
void InOrderTraversal(tree *root)
{
	if(NULL == root)
		return;

	if(root)
	{
		InOrderTraversal(root->lchild);
		printf("%d ", root->data);
		InOrderTraversal(root->rchild);
	}
}

//后序遍历； 左右根
void PostOrderTraversal(tree *root)
{
	if(NULL == root)
		return;

	if(root)
	{
		PostOrderTraversal(root->lchild);
		PostOrderTraversal(root->rchild);
		printf("%d ", root->data);
	}
}

int main(int argc, const char *argv[])
{
	tree *root = createTree(1, 12);
	if(NULL == root)
	{
		printf("malloc failed\n");
		return -1;
	}
	
	dlr(root);					//：1 2 4 8 9 5 10 11 3 6 12 7 
	puts("");

	PreOrderTraversal(root);	//：1 2 4 8 9 5 10 11 3 6 12 7 
	puts("");

	InOrderTraversal(root);		//：8 4 9 2 10 5 11 1 12 6 3 7 
	puts("");

	PostOrderTraversal(root);	//：8 9 4 10 11 5 2 12 6 7 3 1 

	puts("");

	return 0;
}

六、图

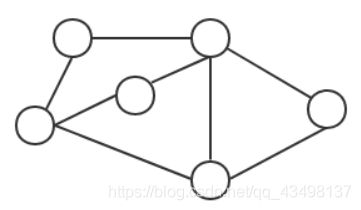
6.1、图的概念

百度云 关于图资料 文档分享：https://pan.baidu.com/s/1lKWWJoe56i3RVNmtHFlsyQ

• 图是非线性的线性表
• 图的存储结构：邻接矩阵
• 图的遍历：深度优先和广度优先

6.2、 图的存储

转载 图的几种存储方式 参考连接：https://blog.csdn.net/weixin_43721423/article/details/86681572

6.3、图的遍历

转载 图的遍历 参考连接：https://www.cnblogs.com/tgycoder/p/5031236.html

6.4、最短路径

迪杰斯特拉 求指定点到所有顶点的最短路径

转载 迪杰斯特拉算法 参考链接：http://data.biancheng.net/view/46.html

七、查询与排序

7.1、 常用的查询算法

顺序查找
折半查找
分块查找
Hash查找

百度云 查询算法 源码分享：https://pan.baidu.com/s/1YXxcHrkS3XGHy_ahYFP-4g

7.2、 常用的排序算法

插入（直插、折半直插）
冒泡
快排

百度云 排序算法 源码分享：https://pan.baidu.com/s/1wkMpKB81Qq2HIgNmG18qNg

转载 常用排序算法总结 参考链接：http://www.cnblogs.com/eniac12/p/5329396.html

八、复杂度

8.1、数据结构与算法的关系

虽然本门课程叫“数据结构”，但经常会讲到算法，以及它们之间的关系。在市面上也经常有诸如“数据结构与算法分析”这样名字的书。

实际上，数据结构与算法是依存关系。只谈数据结构而抛弃算法，则数据是“死”的，没有活力的；只谈算法而抛弃数据结构，则算法无法有所依赖的操作对象，只是空谈。

对于程序来说，数据结构赋予其血肉骨骼，算法赋予其灵魂思想，二者合一才是完整的程序，缺一不可。因此，我们在学习数据结构的时候，经常要学习算法的相关知识。

8.2、算法定义

定义：算法（Algorithm）：算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个动作。

对于给定的问题，是可以有多种算法来解决的。

现实世界中问题千奇百怪，算法当然也就千变万化，没有通用的算法可以解决所有的问题。甚至对于一些问题，优秀的算法却不见得适合它。

例如，对于数据量较少（万以下）的数据排序，快速排序算法的执行效率并没有比冒泡排序快上很多。

8.3、算法示例

辗转相除法求两个正整数的最大公约数

辗转相除法，又名欧几里得算法（Euclidean algorithm），大约3000年前由欧几里得在其著作《几何原本》中提出，是世界上已知最古老的算法。

算法描述：设两数为a、b（a>b），求最大公约数的步骤如下：
1>用a除以b，得到其商q和余数r
2>若r=0，则最大公约数就是b，算法结束
3>若r!=0，则 令a=b，b=r
4>循环执行，回到步骤1

代码描述：
/************
*函数Euclidean_algorithm()
*入参：两个整数int m,int n
*返回值：两数的最大公约数
*功能：计算两个数的最大公约数
**************/

int Euclidean_algorithm(int m,int n)
{
	int r;
	do{
		r=m%n;
		m=n;
		n=r;
	}while(r!=0);
	return m;
}

构造一个算法的常见方法有：递推法、递归法、穷举法、贪心法、分治法、动态规划法、迭代法、分支界限法、回溯法等。

一些大名鼎鼎的算法：
(1)、辗转相除法：已知世界上最古老的算法
(2)、割圆术：刘徽首创，祖冲之改进，计算圆周率
(3)、秦九韶算法：大大简化多项式的计算
(4)、快速排序算法：20世纪十大算法之一
(5)、赫夫曼编码：数据压缩的基本算法
(6)、RSA加密：现代计算机网络数据加密算法的基础
(7)、蒙特卡洛搜索树算法：人工智能基础算法，让计算机“可以像人类般思考”的算法

什么是好的算法？

8.4、算法的空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度记做S(n)=O(f(n))，其中n为问题的规模，f(n)为语句关于n所占存储空间的函数。

例如：写程序实现一个函数PrintN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数

#include 
#include 
#include 
#if 0
void printN(int N)
{
	if(N)
	{
		printN(N-1);
		printf("%d\n", N);
	}
	return;
}
#endif
#if 1

void printN(int N)
{
	int i;
	for(i=1; i<= N;i++)
	{
		printf("%d\n", i);
	}
	return;
}

#endif

int main(int argc, const char *argv[])
{
	int N;
	scanf("%d", &N);

	printN(N);

	return 0;
}

解决问题方法的效率，跟空间的利用效率有关

8.5、算法的时间复杂度

8.5.1、算法的时间复杂度与大O记法
定义：算法的时间复杂度：在进行算法分析时，时间开销T(n)是一个关于问题规模n的函数，进而分析T(n)随n的变化情况确定T(n)的数量级。

算法的时间复杂度记做：T(n)=O(f(n))

它表示随着问题规模n的增大，算法执行时间的增长率和函数f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。

这样用O()来体现算法时间复杂度的记法，我们称之为大O记法。
大O记法表示算法时间复杂度增长率的上限，即随着数据规模n的增大，所耗时的可能最大增长率。

8.5.2、推导大O阶的方法
已知语句执行次数T(n)，推导一个算法时间复杂度大O阶的方法如下：

1>先分析每一条语句的语句频度，进行相加
2>只保留最高阶项
3>如果最高阶项存在且不是1，则去除与这个项相乘的常数

示例：分析以下算法的时间复杂度。求两个n阶方阵乘积

void MATRIXM(int n)
{
	float A[n][n],B[n][n],C[n][n];
	int i,j,k;
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			C[i][j]=0;
			for(k=0;k<n;k++)
			{
				C[i][j]=C[i][j]+A[i][k]*B[j][k];
			}
		}
	}
}

第一步：计算语句执行次数T(n)
对于算法来说，我们要求得语句执行次数，需要先分析每一条语句的语句频度。对于以上代码来说，其每一条语句的语句频度为：

(语句的频度定义：可执行语句在算法中重复执行的次数。执行一次的时间 * 执行的次数)

void MATRIXM(int n)								该语句的语句频度
{
	float A[n][n],B[n][n],C[n][n];
	int i,j,k;
	for(i=0;i<n;i++)-------------------------------->n+1
	{
		for(j=0;j<n;j++)---------------------------->n*(n+1)次
		{
			C[i][j]=0;------------------------------>n^2
			for(k=0;k<n;k++)------------------------>n^2 * (n+1)次
			{
				C[i][j]=C[i][j]+A[i][k]*B[j][k];---->n^3
			}
		}
	}
}

将以上每个语句频度相加，得到 T(n)=2n^3+3*n2+2n+1

第二步：保留最高次项
T(n)----->O(2*n^3)

第三步：去除最高次项系数 T(n)----->O(n^3)

即T(n)=O(n^3)

8.5.3、常见时间复杂度
常数阶O(1)
线性阶O(n)
对数阶O(logN)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
K次方阶O(n^k)
指数阶(2^n)
常用算法的时间复杂度所耗费的时间从小到大依次是：
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

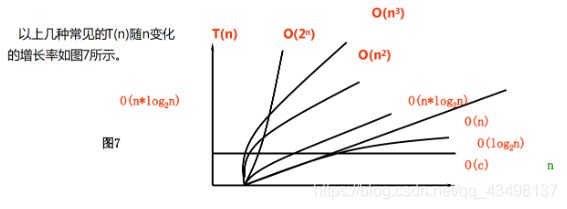
对于O(n^3) 以及以后的时间复杂度，过大的n都会使得算法耗时大大增加，因此过于大的时间复杂度一般不予讨论。

上面的算法并没有随着某个变量的增长而增长，也就是说语句的频度是1，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。

哈希算法就是典型的O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标（不考虑冲突的话）。

第1行会执行n+1次，第2行和第3行会分别执行n次，总的执行时间也就是 3n + 1 次，那它的时间复杂度表示是O(n)。

常见的遍历算法。

可以看到每次循环的时候 i 都会乘2，那么总共循环的次数就是log2n，因此这个代码的时间复杂度为O(logn)。

二分查找（折半）就是O(logn)的算法，每找一次排除一半的可能，256个数据中查找只要找8次就可以找到目标。

线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。

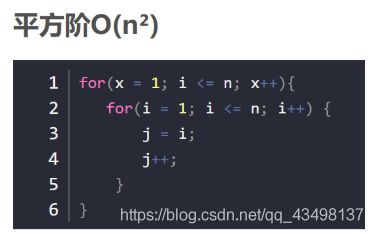
把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了。

冒泡排序，就是典型的O(n^2)的算法，对n个数排序，需要扫描n×n次。

九、数据结构与算法高阶

给大家推荐两本数据结构不错的书

《 数据结构（C语言版 第2版） /21世纪高等学校计算机规划教材》在选材与编排上，贴近当前普通高等院校“数据结构”课程的现状和发展趋势，符合最新研究生考试大纲，内容难度适度，突出实用性和应用性。

《数据结构》算法实现及解析[第二版]高一凡
配合严蔚敏的数据结构很好的一本书，把严蔚敏上的伪码都实现了，很适合初学者。

数据结构与算法PDF下载链接：https://download.csdn.net/download/qq_43498137/22190290

跳转：上一篇、Linux C高级！

跳转：上一篇、Linux C高级！

跳转：下一篇、IO进线程编程！

跳转：下一篇、IO进线程编程！

跳转：开头