机器学习与数据挖掘实验一：牛顿法，梯度下降实现对数几率回归【详细原理+python代码】

系列文章目录

机器学习与数据挖掘实验一：牛顿法，梯度下降实现对数几率回归【详细原理+python代码】
机器学习与数据挖掘实验二：以信息增益为划分准则构造决策树【例题求解】
机器学习与数据挖掘实验三：基于 CNN (VGG，GoogLeNet)的海面舰船图像分类【详细原理+python代码】
机器学习与数据挖掘实验四：基于特征工程的支持向量机分类实验【详细原理+python代码】

---

---

一、 问题重述

基于西瓜数据集3.0构建对率回归模型，通过python语言实现牛顿法和梯度下降法求解此模型，最终，给出求解结果分析。数据如下表所示：

ID	density	Sugar_content	label
1	0.697	0.46	1
2	0.774	0.376	1
3	0.634	0.264	1
4	0.608	0.318	1
5	0.556	0.215	1
6	0.403	0.237	1
7	0.481	0.149	1
8	0.437	0.211	1
9	0.666	0.091	0
10	0.243	0.0267	0
11	0.245	0.057	0
12	0.343	0.099	0
13	0.639	0.161	0
14	0.657	0.198	0
15	0.36	0.37	0
16	0.593	0.042	0
17	0.719	0.103	0

针对以上问题，我将其分为三个部分进行分析：

1. 通过附件西瓜数据集3.0中编号，密度，含糖率，好瓜四列数据，构建判断西瓜的对率回归模型。
2. 通过牛顿法和梯度下降法分别对对率回归模型进行求解。
3. 对 2 中求解结果进行分析对比，并得到最终结论。

二、 实验环境与依赖库

2.1 实验环境

pycharm，python 3.8

2.2 依赖库

• numpy:提供高性能的矩阵运算，实现多维数组计算。
• pandas:从各种文件格式比如CSV、JSON、Excel等导入数据，并进行数据预处理，简单计算等操作。
• matplotlib:绘制函数图像。
• pycallgraph:绘制函数调用关系图。

三、 判断西瓜好坏的对率回归模型

在3.1小节中，我对于附件的西瓜数据进行分析并分成无关数据，标签数据，特征数据三类。在3.2小节中，根据附件提供数据，建立对率回归模型判断对西瓜的好坏进行分类。

3.1 附件西瓜数据分析

对于附件的数据，我们将其分为三类：无关数据，西瓜特征数据，西瓜标签数据。由于西瓜编号与西瓜是否为好瓜无关，因此，我们将其设定为无关数据剔除；同时，西瓜的密度，含糖率与西瓜是否为好瓜密切相关，因此我们将其设定为西瓜特征数据；最后，我们用 0，1 表示西瓜是否为好瓜，当标签为 1 时表示西瓜为好瓜，当标签为 0 时表示西瓜为坏瓜。

3.2 基于对率回归模型的西瓜分类数学原理

进行数据初步分类后，我们构建西瓜是否为好瓜的对率回归模型。我们假设${\mathbf{X}}_{m\times (n+1)}$为西瓜特征矩阵的增广矩阵，其中有m个样本，每个样本具有n个特征。${\beta }_{(n+1)\times 1}$表示逻辑回归模型权重矩阵，${\hat{Y}}_{\mathrm{m}\times 1}$表示西瓜好坏的分类预测结果概率。则对数几率模型计算流程如图所示：

由此，我们得到西瓜好坏判断对率回归模型表达式如下：
$$\hat{\mathbf{Y}}=\frac{1}{1+e^{X\mathbf{\beta }}}$$

四、 对率回归模型求解

在4.1节中，根据概率论知识，利用极大似然法构造代价函数。在4.2节中，通过代价函数最小化构建对率回归模型的目标函数。在4.3节中，针对牛顿法和梯度下降法，分别计算两者的迭代更新公式，求解当目标函数达到最小值时，样本特征权重的值。

4.1 代价函数构建

在3.2节，我们得到了西瓜分类对率回归模型表达式，接下来通过极大似然法估计${\beta }_{(n+1)\times 1}$矩阵的数值。
首先，计算在$y=1$和$y=0$时的后验条件概率如下：

$$p_1(\hat{x};\beta )=p(y=1\mid \hat{x};\beta )=\frac{e^{x\beta }}{1+e^{x\beta }}$$

$$p_0(\hat{x};\beta )=p(y=0\mid \hat{x};\beta )=\frac{1}{1+e^{x\beta }}$$
其中$p_1(\hat{x};\beta )$表示在$\beta$和$\hat{x}$条件下$y=i$的后验条件概率。
然后，我们通过极大似然估计法构造对数函数如下：
$$L(\beta )=\sum _{i=1}^m\ln \left(\mathbf{p}\left(y_i\mid {\mathbf{x}}_i;\beta \right)\right)$$
将后验条件概率带入得：
$$L(\beta )=-\sum _{i=1}^m\left(\ln \left(y_i{e}^{{\hat{x}}_i\beta }+1-y_i\right)-\ln \left(1+e^{{\hat{x}}_i\beta }\right)\right)$$
当$y_i=0$或$y_i=1$时，可以化简得到：

$$L(\beta )=\{\begin{array}{ll}{\sum }_{i=1}^m\left(\ln \left(1+e^{{\hat{\mathbf{x}}}_i\beta }\right)\right),& {\mathbf{y}}_i=0\\ {\sum }_{i=1}^m\left(-{\hat{x}}_i\beta +\ln \left(1+e^{{\hat{x}}_i\beta }\right)\right),& y_i=1\end{array}$$

将两式综合可以得到最终的代价函数如下：
$$L(\beta )=-\sum _{i=1}^m\left(y_i{\hat{x}}_i\beta +\ln \left(1+e^{{\hat{x}}_i\beta }\right)\right)$$

4.2 目标函数构建

当对率回归模型的代价函数越小，则分类结果的误差越小。因此为了使得代价函数达到最小，构建如下目标函数：
$${\beta }^{\ast }=\underset{\beta }{\mathrm{argmin}}\mathbf{L}(\mathbf{\beta })$$

4.3 对率回归模型求解

根据凸优化理论，我们采用牛顿法和梯度下降法两种方法求解使得代价函数达到最小值时的 ${\mathbf{\beta }}^{\ast }$。

4.3.1 牛顿法迭代函数原理

首先，我们计算 ${\beta }_{(n+1)\times 1}$的一阶导数和二阶导数如下：
$$\frac{L(\beta )}{\partial \beta }=\left[\frac{\partial L}{\partial {\beta }_1},\frac{\partial L}{\partial {\beta }_2},\dots \dots .,\frac{\partial L}{\partial {\beta }_n}\right]$$
$$\frac{{\mathbf{L}}^2(\mathbf{\beta })}{\partial \mathbf{\beta }\partial {\mathbf{\beta }}^{\mathbf{T}}}=\left[\begin{array}{cccc}\frac{{\partial }^{2}L}{\partial {\beta }_1^2}& \frac{{\partial }^{2}L}{\partial {\beta }_1{\beta }_2}& \cdots & \frac{{\partial }^{2}L}{\partial {\beta }_1{\beta }_n}\\ \frac{{\partial }^{2}L}{\partial {\beta }_2{\beta }_1}& \frac{{\partial }^{2}L}{\partial {\beta }_2^2}& \cdots & \frac{{\partial }^{2}L}{\partial {\beta }_2{\beta }_n}\\ \frac{{\partial }^{2}L}{\partial {\beta }_n{\beta }_1}& \frac{{\partial }^{2}L}{\partial {\beta }_n{\beta }_2}& \cdots & \frac{{\partial }^{2}L}{\partial {\beta }_n^2}\end{array}\right]$$

其次，我们将目标函数进行包含二阶导数的泰勒展开，如下：
$$\mathrm{L}(\beta +\Delta \beta )=L(\beta )+\Delta {\beta }^T\frac{\partial L}{\partial \beta }+\frac{1}{2}\Delta {\beta }^T\frac{{\partial }^{2}L}{\partial {\beta }^2}\Delta \beta$$
根据函数最小值性质，当偏导数为0时，函数取得最值。因此得到：

$$\frac{L(\beta )}{\partial \beta }=0\frac{L^2(\beta )}{\partial \beta \partial {\beta }^T}=0$$

$$\Delta {\beta }^T\frac{\partial \mathrm{L}}{\partial \beta }+\frac{1}{2}\Delta {\beta }^T\frac{{\partial }^2\mathrm{L}}{\partial {\beta }^2}\Delta \beta =0$$
将其化简可得：

$$\Delta {\beta }^T\frac{\partial L}{\partial \beta }=-\Delta {\beta }^T\frac{{\partial }^{2}L}{\partial {\beta }^2}\Delta \beta \iff \Delta \beta =-{\left(\frac{{\partial }^{2}L}{\partial {\beta }^2}\right)}^{-1}\frac{\partial L}{\partial \beta }$$

由此，我们得到牛顿法的梯度下降公式如下：

$${\beta }^T={\beta }^{T+1}+\Delta \beta \iff {\beta }^{T+1}={\beta }^T-\Delta \beta \iff {\beta }^{T+1}={\beta }^T-{\left(\frac{{\partial }^{2}L}{\partial {\beta }^2}\right)}^{-1}\frac{\partial L}{\partial \beta }$$

4.3.2 梯度下降法迭代函数推导

首先，我们构建梯度 $\nabla L(\beta )$，它表示当前函数位置的导数，即函数在该点处的方向导数沿该方向可以取得较大值。

$$\nabla L(\beta )=\frac{dL(\beta )}{d\beta }$$
然后将目标函数进行包含一阶导数的泰勒展开，公式如下：

$$L(\beta )=L\left({\beta }_0\right)+\left(\beta -{\beta }_0\right)\cdot \nabla L\left({\beta }_0\right)$$
我们采用一个单位向量$v$与标量$\alpha $的内积表示。 $\mathbf{\beta }-{\mathbf{\beta }}_o$，公式如下：

$$\beta -{\beta }_0=\alpha v$$
将其带入泰勒展开式，化简如下：

$$L(\beta )=L\left({\beta }_0\right)+\alpha v\cdot \nabla L\left({\beta }_0\right)$$
为使得目标函数达到最小值，我们可以得知 $L(\beta )<L\left({\beta }_0\right)$，因此 $\alpha v\nabla L\left({\beta }_0\right)<0$，此时 $\nabla L\left({\beta }_0\right)$与$v$方向相反，因此可以得到两者之间的关系为：

$$v=-\frac{\nabla L\left({\beta }_0\right)}{\Vert \nabla L\left({\beta }_0\right)\Vert }.$$
将其带入 $\beta -{\beta }_0=\alpha v$得：

$$\beta ={\beta }_0-\alpha \frac{\nabla L\left({\beta }_0\right)}{\Vert \nabla L\left({\beta }_0\right)\Vert }={\beta }_0-{\alpha }^{\prime }\nabla L\left({\beta }_0\right)$$
由此，我们得到迭代公式如下：

$${\beta }^{T+1}={\beta }^{\top }-\alpha \nabla L\left({\beta }_0\right)$$

五、 对率回归模型求解代码实现

在5.1小节，概述对率回归模型求解LogisticRegression类的基本框架，并通过类图绘制其包含的操作函数。在5.2小节，对于构造函数，数据读取函数，迭代方法选择函数进行了详细描述并给出代码。在5.3和5.4小节，概述了牛顿法和梯度下降法求解对率回归模型的函数调用关系以及算法流程，并在附上两者实现的核心函数代码。在5.5小节，通过sklearn库中的逻辑回归模型LogisticRegression训练数据集得到sklearn机器学习库的训练结果。

5.1 对率回归模型程序框架

5.1.1 LogisticRegression类

为实现对率回归模型求解，我新建文件LogisticRegression.py，并在其中中创建LogisticRegression类，其中包含五类函数用于求解对率回归模型，LogisticRegression类结构如图所示。在接下来的4个小节中，我将对其中主要函数进行说明。

5.2 基本函数说明

5.2.1 构造函数.

对于构造函数init()，首先初始化特征权重$\beta$矩阵为[1,1,1]，误差阈值默认为1e-5，代价函数最小化求解方法为梯度下降法，代码如下：

def __init__(self, method="gradientdescent", err = 1e-5):
		# beta:特征权重，初始化为[1,1,1]
		# method:选择方法，包括牛顿法和梯度下降法以及sklearn方法
		# err：误差，默认1e-5
		self.beta = beta = np.ones((1, 3))
		self.method = method
		self.err = err

5.2.2 读取特征和标签数据

对于西瓜数据的读取，在这里我采用pandas库对附件watermelon3.0alpha.csv中数据进行读取，其中返回值表示西瓜特征向量$X$，标签向量$Y$以及DataFrame类型的西瓜原始数据data。其中原始数据用于绘图使用，西瓜特征向量和标签向量用于训练对率回归模型使用。其代码如下：

def read_watermelon_data(self,filename):
		data=pd.read_csv(filename)
		Xtrain=data[["density","Sugar_content"]]
		Ytrain=data["label"]
		X=np.array(Xtrain)
		Y=np.array(Ytrain).reshape((len(Ytrain),1))
		return data,X,Y

5.2.3 迭代方法选择函数

对于迭代方法选择函数，我们通过根据构造函数中self.method的取值分别调用self.newton，self.gradient，self.sklearn_method方法，如果self.method的值不在三个取值范围之中，则抛出异常。实现代码如下：

def fit(self, X, Y):
		if self.method == "newton":
				return self.newton(X, Y)
		elif self.method == "gradientdescent":
				return self.gradient(X, Y)
		elif self.method=="sklearn":
				return self.sklearn_method(X,Y)
		else:
				raise ValueError('Unknown method!')

5.2.4 迭代求解实现函数

在迭代求解实现时，创建了三种类型的函数，self.newton，self. gradient，self. sklearn_method，对于这三种方法的实现，我将在下一小节进行说明。

5.3 牛顿法求解实现

5.3.1 牛顿法算法核心.

首先，给出牛顿法算法核心流程图，如图所示。

初始化权重矩阵为[ 1 , 1 , 1 ]并设定误差阈值（默认1e-5），然后计算代价函数对权重矩阵beta的一阶导数和二阶导数，带入牛顿法的迭代公式对beta进行更新，当更新前的代价值与更新后的代价值相差小于阈值时，停止迭代，输出结果。

5.3.2 牛顿法python实现

通过pycallgraph类绘制牛顿法运行函数调用示意图如图所示。

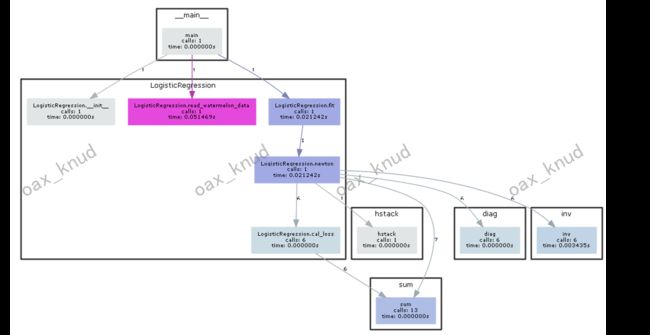
首先，初始化LogisticRegression类，创建optmizer1对象并设置其方法为newton，然后调用optmizer1.newton函数实现牛顿法迭代求解最小代价时的权重矩阵。
对于newton函数的实现，首先将西瓜特征矩阵$X$增加一列，生成增广矩阵X1，然后初始化原始代价值old_l为0，调用cal_loss(Y,z)函数计算beta权重矩阵下的新代价值new_l。循环计算代价函数对于权重矩阵beta的一阶导数first_order和二阶导数second_order，并通过牛顿法的迭代公式更新beta矩阵的值。然后更新old_l并调用cal_loss(Y,z)更新new_l，当old_l - new_l的绝对值小于误差阈值时，跳出循环并得到最终的beta值。实现代码如下：

def newton(self, X, Y):
		N = X.shape[0] #获取样本个数N
		one = np.ones((N, 1)) #生成[N,1]的数值为1的向量
		X1 = np.hstack([X, one]) #生成X的增广矩阵
		z = X1.dot(self.beta.T) #生成[N,1]的点乘向量
		old_l = 0 #初始化代价函数初值为0
		new_l = self.cal_loss(Y,z) #计算对数似然的代价函数值
		iters = 0#迭代次数
		while(np.abs(old_l - new_l) > self.err):#当两次代价函数值之差大于设定误差阈值时，停止迭代
		#计算y=1的后验概率，得到[N, 1]的p1向量
		p1 = np.exp(z) / (1 + np.exp(z))
		#y=1的后验概率和y=0的后验概率相乘并将其格式调整为 [1,N],然后生成对角矩阵[N, N]
		p = np.diag((p1 * (1-p1)).reshape(N))
		#计算L对于beta的一阶导数，生成[1, d+1]向量
		first_order = -np.sum(X1 * (Y - p1), 0, keepdims=True)
		#计算L对于beta的二阶导数，生成[d+1, d+1]向量
		second_order = X1.T.dot(p).dot(X1)
		#更新beta，迭代函数
		self.beta -= first_order.dot(np.linalg.inv(second_order))
		#更新代价函数
		z = X1.dot(self.beta.T)
		old_l = new_l
		new_l = self.cal_loss(Y,z)
		iters += 1#增加迭代次数
		return self.beta

5.4 梯度下降法.

5.4.1 梯度下降法算法核心

梯度下降法的核心算法流程如图所示。首先，初始化权重矩阵，设定误差阈值（默认1e-5）以及学习率$\alpha$（默认0.5），然后计算代价函数对权重矩阵beta的一阶导数，并对beta进行迭代更新。当更新前的代价值与更新后的代价值相差小于阈值时，停止迭代，输出结果。

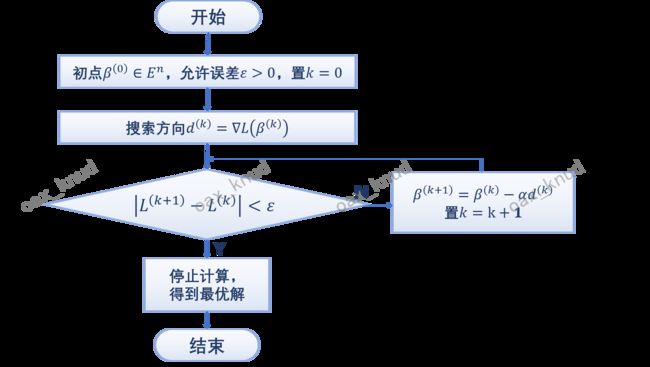
5.4.2 梯度下降法python实现

通过pycallgraph绘制梯度下降法运行函数调用图，如图所示。

首先，初始化LogisticRegression类，创建optmizer2对象并设置其方法为gradientdescent，然后调用optmizer2.newton函数实现梯度下降法迭代求解最小代价时的权重矩阵。
对于gradient函数的实现，首先将西瓜特征矩阵X增加一列，生成增广矩阵X1，然后初始化原始代价值old_l为0，调用cal_loss(Y,z)函数计算beta权重矩阵下的新的代价值new_l。循环计算代价函数对于权重矩阵beta的一阶导数first_order，并通过 函数更新beta矩阵的值（α为学习率），然后更新old_l并调用cal_loss(Y,z)更新new_l，当old_l - new_l的绝对值小于误差阈值时，跳出循环并得到最终的beta值。实现代码如下：

def gradient(self, X, Y, learn_rate=0.5):
		N = X.shape[0] #获取样本个数N
		one = np.ones((N, 1)) #生成[N,1]的数值为1的向量
		X1 = np.hstack([X, one]) #生成X的增广矩阵
		z = X1.dot(self.beta.T) #生成[N,1]的点乘向量
		old_l = 0 #初始化代价函数初值为0
		new_l = self.cal_loss(Y,z)   #计算对数似然的代价函数值
		iters = 0
		while(np.abs(old_l - new_l) > self.err):
		p1 = np.exp(z) / (1 + np.exp(z))#计算y=1的后验概率，得到[N, 1]的p1向量
		p = np.diag((p1 * (1-p1)).reshape(N))
		first_order = -np.sum(X1 * (Y - p1), 0, keepdims=True)
		#更新beta，迭代函数
		self.beta -= learn_rate * first_order
		z = X1.dot(self.beta.T)
		old_l = new_l
		new_l = self.cal_loss(Y,z)
		iters += 1
		return self.beta

5.5 机器学习sklearn库实现.

在sklearn库中，可以通过LogisticRegression类实现对于逻辑回归模型的求解。我们首先通过from sklearn.linear_model import LogisticRegression引入sklearn中LogisticRegression包，然后初始化逻辑回归模型，设置迭代求解方法为lbfgs（拟牛顿法），然后调用fit方法对西瓜数据集进行训练，最终得到权重矩阵beta。其代码如下：

def sklearn_method(self, X, Y):
		from sklearn.linear_model import LogisticRegression
		reg = LogisticRegression(solver='lbfgs', C=1000).fit(X, Y)
		self.beta = np.c_[reg.coef_, reg.intercept_]
		print("sklearn中使用lbfgs方法权重矩阵：",self.beta)
		return self.beta
\end{lstlisting}

六、 结果分析

6.1 定性结果分析

通过matplotlib中scatter函数以及plot函数绘制不同种类西瓜的散点图以及三种方法求解逻辑回归的结果图。如图所示：

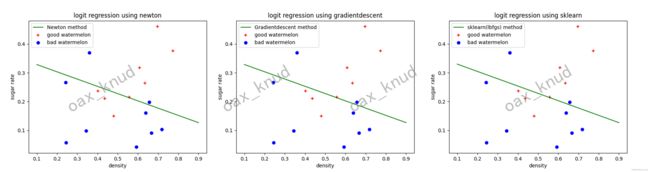
通过观察图可以发现，numpy实现的牛顿法，梯度下降法以及sklearn实现的拟牛顿法求解逻辑回归时，对于西瓜好坏的分类效果基本相当。三者对于好瓜的分类均存在3个样本的误判，对于坏瓜的分类存在1个样本的误判，准确率在76.47左右。准确率之所以不高的原因在于附件样本数据过少，只有17个。

6.2 定量结果分析

对于三种方法，输出其迭代次数，最终代价函数值以及beta矩阵进行定量分析，如下表：

方法	迭代次数	最终代价值	Beta权重矩阵
牛顿法	4	8.6836	[3.148203，12.485565，4.4154285]
梯度下降法	242	8.6841	[3.106223，12.3094587，4.3562010]
Sklearn	9	/	[3.039079，11.955709，4.2495913]

sklearn中未查询到计算逻辑回归最终代价值的属性，因此未计算。
对比三种方法的迭代次数以及最终权重矩阵beta，我们可以得到以下结论：

• 迭代次数对比：牛顿法和sklearn中lbgfs方法迭代次数较少，而梯度下降法在同等条件下迭代次数较多，耗费时间较长。

• 代价函数值对比：牛顿法和梯度下降法最终得到得代价值均为8.68左右，相差较小。因此其迭代效果可以认为基本相等。

• 特征权重矩阵对比：通过表，我们可以得出三种方法计算出得权重矩阵的值基本上稳定在 3 ，12 ，4 附近，相差较小。根据权重矩阵，我们可以得到三种方法的各指标权重以及常数项如表所示。

方法	Density权重	Sugar_content权重	常数
牛顿法	3.148203	12.485565	4.
梯度下降法	3.106223	12.3094587	4.
Sklearn	3.039079	11.955709	4.

附录

LogisticRegression代码实现

# -*- coding: utf-8 -*-
"""
@Time ： 2022-03-18 10:37
@Author ： oax_knud
@File ：LogisticRegression1.py
@IDE ：PyCharm
"""
#依赖库
"""
numpy:向量运算
matplotlib:绘图
pandas:读取csv文件数据
"""
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pycallgraph import PyCallGraph
from pycallgraph.output import GraphvizOutput
from pycallgraph import Config
from pycallgraph import GlobbingFilter


#构造逻辑回归类
class LogisticRegression(object):
		def __init__(self, method="gradientdescent", err = 1e-5):
				# 初始化
				"""
				beta:特征权重，初始化为[1,1,1]
				method:选择方法，包括牛顿法和梯度下降法
				eps：误差，默认1e-5
				"""
				self.beta = beta = np.ones((1, 3))
				self.method = method
				self.err = err
		#选择方法
		def fit(self, X, Y):
				"""
				param X: 西瓜特征数据
				param Y: 标签数据
				return: 逻辑回归特征权重beta
				"""
				if self.method == "newton":
				return self.newton(X, Y)
				elif self.method == "gradientdescent":
				return self.gradient(X, Y)
				elif self.method=="sklearn":
				return self.sklearn_method(X,Y)
				else:
				raise ValueError('Unknown method!')
		#计算代价函数
		def cal_loss(self,Y,z):
				"""
				:param Y: [N,1]Y向量，N表示样本个数，1表示标签个数
				:param z: X增广矩阵点成beta，生成[N,1]的点乘向量
				return: 代价函数值
				"""
				return np.sum(-Y*z + np.log(1+np.exp(z)))
		
		#牛顿法
		def newton(self, X, Y):
				"""
				param X: [N,d]X向量，N表示样本个数，d表示特征个数
				param Y: [N,1]Y向量，N表示样本个数，1表示标签个数
				return: [1,d+1]beta向量，特征权重向量(包括权重和常数)
				"""
				N = X.shape[0] #获取样本个数N
				one = np.ones((N, 1)) #生成[N,1]的数值为1的向量
				X1 = np.hstack([X, one]) #生成X的增广矩阵
				z = X1.dot(self.beta.T) #生成[N,1]的点乘向量
				old_l = 0 #初始化代价函数初值为0
				new_l = np.sum(-Y*z + np.log(1+np.exp(z))) #计算对数似然的代价函数值
				iters = 0#迭代次数
				while(np.abs(old_l - new_l) > self.err):#当两次代价函数值之差大于设定误差阈值时，停止迭代
				#计算y=1的后验概率，得到[N, 1]的p1向量
				p1 = np.exp(z) / (1 + np.exp(z))
				#y=1的后验概率和y=0的后验概率相乘并将其格式调整为 [1,N],然后生成对角矩阵[N, N]
				p = np.diag((p1 * (1-p1)).reshape(N))
				#计算L对于beta的一阶导数，生成[1, d+1]向量
				first_order = -np.sum(X1 * (Y - p1), 0, keepdims=True)
				#计算L对于beta的二阶导数，生成[d+1, d+1]向量
				second_order = X1.T.dot(p).dot(X1)
				
				#更新beta，迭代函数
				self.beta -= first_order.dot(np.linalg.inv(second_order))
				#更新代价函数
				z = X1.dot(self.beta.T)
				old_l = new_l
				new_l = self.cal_loss(Y,z)
				iters += 1#增加迭代次数
				print("牛顿法收敛的迭代次数: ", iters)
				print('牛顿法收敛后对应的代价函数值: ', new_l)
				print("牛顿法收敛后对应的权重矩阵:",self.beta)
				return self.beta
				
		#梯度下降法
		def gradient(self, X, Y, learn_rate=0.5):
				"""
				param X: [N,d]X向量，N表示样本个数，d表示特征个数
				param Y: [N,1]Y向量，N表示样本个数，1表示标签个数
				learn_rate:学习率，默认0.5
				return: [1,d+1]beta向量，特征权重向量(包括权重和常数)
				"""
				N = X.shape[0] #获取样本个数N
				one = np.ones((N, 1)) #生成[N,1]的数值为1的向量
				X1 = np.hstack([X, one]) #生成X的增广矩阵
				z = X1.dot(self.beta.T) #生成[N,1]的点乘向量
				old_l = 0 #初始化代价函数初值为0
				new_l = self.cal_loss(Y,z)   #计算对数似然的代价函数值
				iters = 0
				while(np.abs(old_l - new_l) > self.err):
				#计算y=1的后验概率，得到[N, 1]的p1向量
				p1 = np.exp(z) / (1 + np.exp(z))
				#y=1的后验概率和y=0的后验概率相乘并将其格式调整为 [1,N],然后生成对角矩阵[N, N]
				p = np.diag((p1 * (1-p1)).reshape(N))
				#计算L对于beta的一阶导数，生成[1, d+1]向量
				first_order = -np.sum(X1 * (Y - p1), 0, keepdims=True)
				#更新beta，迭代函数
				self.beta -= learn_rate * first_order
				z = X1.dot(self.beta.T)
				old_l = new_l
				new_l = self.cal_loss(Y,z)
				iters += 1
				print("梯度下降法收敛的迭代次数iters: ", iters)
				print('梯度下降法收敛后对应的代价函数值: ', new_l)
				print("梯度下降法收敛后对应的权重矩阵:", self.beta)
				return self.beta
		
		def sklearn_method(self, X, Y):
				'''
				sklearn 模块中的lbfgs方法求beta
				param X:(x,1) shape[N,d+1]
				@param Y:label shape[N,1]
				@return beta (w,b) shape [1,d+1]
				'''
				from sklearn.linear_model import LogisticRegression
				# print("请选择使用的求解方法：")
				# print("1:lbfgs,拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数")
				reg = LogisticRegression(solver='lbfgs', C=1000).fit(X, Y)
				self.beta = np.c_[reg.coef_, reg.intercept_]
				print("sklearn中使用lbfgs方法权重矩阵：",self.beta)
				print("iter:",reg.n_iter_)
				return self.beta
		
		def read_watermelon_data(self,filename):
				'''
				读取西瓜数据并转换
				filename:数据文件
				return:
				param data:pandas形式原始数据
				param X: [N,d]X向量，N表示样本个数，d表示特征个数
				param Y: [N,1]Y向量，N表示样本个数，1表示标签个数
				'''
				data=pd.read_csv(filename)
				Xtrain=data[["density","Sugar_content"]]
				Ytrain=data["label"]
				X=np.array(Xtrain)
				Y=np.array(Ytrain).reshape((len(Ytrain),1))
				return data,X,Y
		
if __name__ == "__main__":
		filename="watermelon3.0alpha.csv"
		print("请选择使用求解逻辑回归模型的方法：")
		print("1:牛顿法")
		print("2:梯度下降法")
		print("3:机器学习sklearn库调用")
		num=int(input())
		if num==1:
				#牛顿法
				graphviz = GraphvizOutput()
				graphviz.output_file = 'newton.png'
				with PyCallGraph(output=graphviz):
						optmizer1=LogisticRegression("newton")
						data,X, Y = optmizer1.read_watermelon_data(filename)
						beta_newton=optmizer1.fit(X,Y)
				#绘图
				label1 = np.array(data[data["label"]==1])
				label0 = np.array(data[data["label"]==0])
				plt.scatter(label1[:, 1], label1[:, 2], c='r', marker='+',label="good watermelon")
				plt.scatter(label0[:, 1], label0[:, 2], c='b', marker='o',label="bad watermelon")
				ymin = -(beta_newton[0, 0] * 0.1 + beta_newton[0, 2]) / beta_newton[0, 1]
				ymax = -(beta_newton[0, 0] * 0.9 + beta_newton[0, 2]) / beta_newton[0, 1]
				plt.plot([0.1, 0.9], [ymin, ymax], 'g-', label='Newton method')
				plt.xlabel('density')
				plt.ylabel('sugar rate')
				plt.title("logit regression using newton")
				plt.legend()
				plt.show()
		elif num==2:
		#梯度下降法
				graphviz = GraphvizOutput()
				graphviz.output_file = 'grad.png'
				with PyCallGraph(output=graphviz):
						optmizer2=LogisticRegression("gradientdescent")
						data,X, Y = optmizer2.read_watermelon_data(filename)
						beta_grad=optmizer2.fit(X,Y)
				#绘图
				label1 = np.array(data[data["label"]==1])
				label0 = np.array(data[data["label"]==0])
				plt.scatter(label1[:, 1], label1[:, 2], c='r', marker='+',label="good watermelon")
				plt.scatter(label0[:, 1], label0[:, 2], c='b', marker='o',label="bad watermelon")
				ymin = -(beta_grad[0, 0] * 0.1 + beta_grad[0, 2]) / beta_grad[0, 1]
				ymax = -(beta_grad[0, 0] * 0.9 + beta_grad[0, 2]) / beta_grad[0, 1]
				plt.plot([0.1, 0.9], [ymin, ymax], 'g-', label='Gradientdescent method')
				plt.xlabel('density')
				plt.ylabel('sugar rate')
				plt.title("logit regression using gradientdescent")
				plt.legend()
				plt.show()
		elif num==3:
		#梯度下降法
				optmizer3=LogisticRegression("sklearn")
				data,X, Y = optmizer3.read_watermelon_data(filename)
				beta_sklearn=optmizer3.fit(X,Y)
				#绘图
				label1 = np.array(data[data["label"]==1])
				label0 = np.array(data[data["label"]==0])
				plt.scatter(label1[:, 1], label1[:, 2], c='r', marker='+',label="good watermelon")
				plt.scatter(label0[:, 1], label0[:, 2], c='b', marker='o',label="bad watermelon")
				ymin = -(beta_sklearn[0, 0] * 0.1 + beta_sklearn[0, 2]) / beta_sklearn[0, 1]
				ymax = -(beta_sklearn[0, 0] * 0.9 + beta_sklearn[0, 2]) / beta_sklearn[0, 1]
				plt.plot([0.1, 0.9], [ymin, ymax], 'g-', label='sklearn(lbfgs) method')
				plt.xlabel('density')
				plt.ylabel('sugar rate')
				plt.title("logit regression using sklearn")
				plt.legend()
				plt.show()
		else:
		print("error")