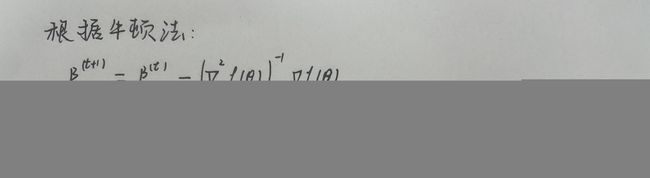铖铖的花嫁

机器学习之逻辑回归原理详解、公式推导（手推）、简单实例（牛顿法，梯度下降法，随机梯度法，sklearn调包）

1. 逻辑回归原理
2. 前置知识
- 2.1. 极大似然法
- 2.2. 梯度下降法
- 2.3. 牛顿法
3. 公式推导
4. 简单实例
- - 4.0. 数据集
  - 4.1. 逻辑回归
  - 4.2. 梯度下降求解
  - 4.3. 随机梯度下降求解
  - 4.4. 牛顿法求解
  - 4.5 sklearn
5. 运行（可直接食用）
参考

1. 逻辑回归原理

我们知道机器学习问题大致可以分为3大类：分类、回归、聚类。

我们之前提到过的线性回归就是非常经典的一种回归，那么问题来了，逻辑回归属于机器学习的哪类算法？
需要注意的是，虽然名字里带了个回归，但是逻辑回归是实打实的分类算法。

讲到这里，相信大家都会有这样的疑问：作为最简单的分类算法，逻辑回归算法跟最简单的回归算法线性回归有什么关系？
其实两者的关系还是比较密切的，因为逻辑回归实际上就是往线性回归的式子上套了个函数（如对数几率函数），也就是函数的复合。
当然我们套在外面的这层对数几率函数并不是随便选一个就好了，我们对它肯定是有要求的：

连续可导：这也是为什么西瓜书中会选择 sigmoid 函数代替单位阶跃函数，也是为什么 $\lvert x \rvert$ 在机器学习很多地方都不被推荐。
对率回归求导的目标函数任意阶可导：由此可见， $x^2$ 等函数也不被推荐，横向对比我们更能发现 sigmoid 函数的性质很好，虽然这并不意味着这里只有 sigmoid 函数才是最好的。

再提逻辑回归的优点：

它是直接对分类的可能性建模，所以无需事先假设数据分布，也避免了假设分布不准确带来的一系列问题。
它不仅能预测出“类别”，还可以得到近似概率的预测，这对许多利用概率辅助决策的任务很有用。

此外，因为不用假设分布、且因变量是概率，当然最重要的原因是用到了logit变换，逻辑回归特别适合二分类问题。

2. 前置知识

如果上来直接推导公式，可能对高数和概率论知识掌握不完全的读者不太友好，这里复习下几个会用到的方法。

2.1. 极大似然法

这个是概率论的知识，我们在后面会用它来估计参数。最大似然估计的目的就是：利用已知的样本结果，反推最有可能导致这个结果的参数。
$\theta_{c})$ 表示在由参数 $\theta_{c}$ 决定的条件c被满足的情况下，x 事件发生的概率。我们假设这些独立同分布的x事件组成的集合为 D，那么这个 D 发生的概率就可以表示为：
$\theta_{c}) = \prod_{x \in D}P(x| \theta_{c})$
极大似然法的目标是找到一个 $\theta_c$ ，使得事件 D 出现的可能性最大，所以为了好算，我们把连乘符号用 log 变成连加符号，称为对数似然。
$\theta_{c}) = \sum_{x \in D}log\ P(x| \theta_{c})$
最终的目的就转化为求极大似然估计参数 $\theta_c$ 的最大估计的估计参数 $\hat{\theta}_c$ ，表示为：
$\hat{\theta}_c=arg_{\theta_c}max LL( \theta_{c})$

2.2. 梯度下降法

我们将用梯度下降法求参数的最优解。
梯度下降法的思路其实就是不断地迭代，一直沿着当下最陡的方向前进，在迭代n次之后就会到达最小值。如下图所示，我们将从A1点到A2点到A3点，一步一步接近最小值。当然也可能陷入局部最优。

以二元函数 $z = f (x, y) $ 为例，假设其对每个变量都具有连续的一阶偏导数 $\frac{\partial z} {\partial x}$ 和 $\frac{\partial z} {\partial y}$ ，则这两个偏导数构成的向量 $\left [ \frac{\partial z} {\partial x},\frac{\partial z} {\partial y} \right ]$ 即为该二元函数的梯度向量，一般记作 $\nabla f\left ( x,y \right )$ 。
接下来只需要按照学习率a，往固定的方向前进，直到找到最低点。

2.3. 牛顿法

我们将用牛顿法求参数的最优解。
主要思路就是先对目标函数在 $x_0$ 点泰勒展开。忽略次数较高的项，直接对式子两边求梯度得到梯度向量。使梯度向量为0，就可以求得下一个点的位置。不断进行这个迭代，直到梯度的模趋于于0，或者函数值下降小于指定阈值。

这么看来牛顿法也存在被卡在局部最优的问题，所以牛顿法的初始点最好能够足够靠近最低点。

3. 公式推导

我们先根据逻辑回归的思路推导出 $\beta$ 的表达式

我们的目标是解出最大概率时参数 $\beta$ ，一般用梯度下降法或者牛顿法计算。

梯度下降法

牛顿法

4. 简单实例

4.0. 数据集

以西瓜数据集为例（我们把它存为csv，方便以后用）

watermelonData.csv

x1,x2,x3,x4,x5,x6,label
0,0,0,0,0,0,1
1,0,1,0,0,0,1
1,0,0,0,0,0,1
0,0,1,0,0,0,1
2,0,0,0,0,0,1
0,1,0,0,1,1,1
1,1,0,1,1,1,1
1,1,0,0,1,0,1
1,1,1,1,1,0,0
0,2,2,0,2,1,0
2,2,2,2,2,0,0
2,0,0,2,2,1,0
0,1,0,1,0,0,0
2,1,1,1,0,0,0
1,1,0,0,1,1,0
2,0,0,2,2,0,0
0,0,1,1,1,0,0

4.1. 逻辑回归

附上回归函数

# 其实就是sigmoid函数
# (m, n), (n, 1) => (m, 1)
def get_logic(data, w):
    return 1 / (1 + np.exp((-1) * np.dot(data, w)))

4.2. 梯度下降求解

对着之前的公式我们完成梯度下降算法，并画出损失函数

def my_gradient(data, w, label, lr=0.001, epoch=250):
    # 这里对应对数似然函数的平均损失
    def cost():
        left = np.dot(label.T, np.dot(data, w))
        right = np.log(sum(1 + np.exp(np.dot(data, w))))
        return float((left - right) / data.shape[0])

    # 这里是之前求偏导的结果
    def gredient():
        # (m, 1)
        hx = get_logic(data, w)
        # (m, 1)
        error = hx - label
        grad = np.matmul(error.T, data)
        return grad

    cost_list = []
    # 梯度下降终止的条件有很多，我们这里就直接简化，在迭代次数到了的时候直接结束
    for i in range(epoch):
        grad = gredient()
        w = w - lr * grad.T
        cost_list.append((cost()))
    return w, cost_list


def eveluate(predict, result):
    correct = 0
    for i in range(predict.shape[0]):
        correct += (int(predict[i][0]+0.5) == result[0])
    print("准确率为：", correct / predict.shape[0] * 100, "%")


def draw_cost(cost_list):
    print(cost_list)
    plt.plot([i for i in range(len(cost_list))], cost_list, label='Frist line', linewidth=3, color='r', marker='o', markerfacecolor='blue', markersize=12)
    plt.show()

epoch可以小一点，损失已经开始往上了。

4.3. 随机梯度下降求解

随机梯度下降是每次迭代使用一个样本来对参数进行更新，其实我也不是特别理解这个算是哪门子的优化，感觉有利有弊吧，收敛的应该会快点，但是没有充分考虑全局。
画图和准确率函数同上。

def random_gradient(data, w, label, lr=0.001, epoch=4000):
    # 修改楼上的函数
    def cost():
        left = np.dot(label.T, np.dot(data, w))
        right = np.log(sum(1 + np.exp(np.dot(data, w))))
        return float(left - right)

    # 修改楼上的函数
    def gredient(i):
        hx = get_logic(data[i], w)
        error = hx - label[i]
        grad = error * data[i]
        return grad.reshape(-1,1)

    cost_list = []
    # 这里我们加入随机
    for i in range(epoch):
        grad = gredient(random.randint(0, data.shape[0]-1))
        w = w - lr * grad
        cost_list.append(cost())
    return w, cost_list

效果如下，说实话并没有感觉有什么优化。

4.4. 牛顿法求解

个人认为牛顿法要好一点，因为考虑到了2阶导，收敛速度相对快一点且不容易陷入局部最优。
为了方便编程，我们把海森矩阵化成乘积形式：

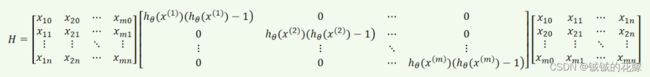
一阶导化为：

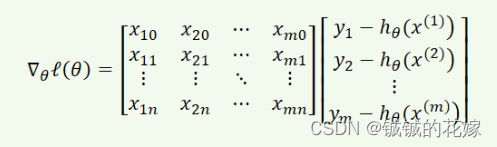
def my_newton(data_train, w, label_train, epoch=2):
    def my_loss(theta):
        z = data_train.dot(theta)
        probs = get_logic(data_train, theta)
        data_loss = np.power((probs - label_train), 2)
        return 0.5 * np.sum(data_loss)

    cost_list = []
    for i in range(epoch):
        # 逻辑函数
        hx = get_logic(data_train, w)
        # 求一阶导(n*1)
        first = data_train.T.dot(label_train-hx)
        # 对角矩阵(m*m)
        dia = np.diagflat(hx*(hx-np.ones(data_train.shape[0]).reshape(data_train.shape[0], 1)))
        # 海森矩阵(n*n)
        H = np.dot(data_train.T.dot(dia), data_train)
        w = w - np.linalg.solve(H, first)
        cost_list.append(my_loss(w))
    return w, cost_list

不知道是我的代码的问题还是其他原因，牛顿法求解的时候会遇到奇异矩阵的问题，这就导致了牛顿法的epoch不能设置的很高。希望路过的大佬在评论区指正。

4.5 sklearn

机器学习包直接用

def sk(data_train, label_train):
    # 定义模型
    logic_model = LogisticRegression(max_iter=5, random_state=1129)
    # 训练模型
    logic_model = logic_model.fit(data_train, label_train)
    return logic_model.coef_.T

效果如下

5. 运行（可直接食用）