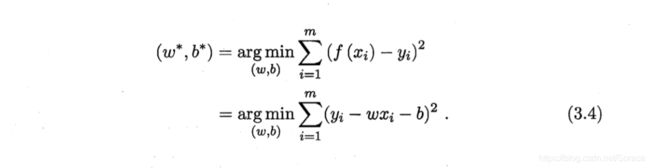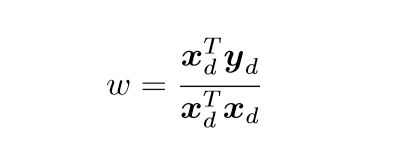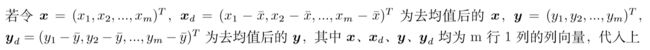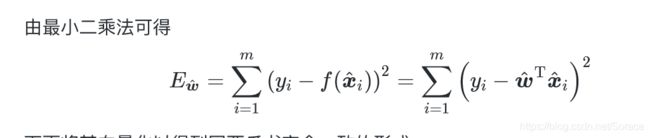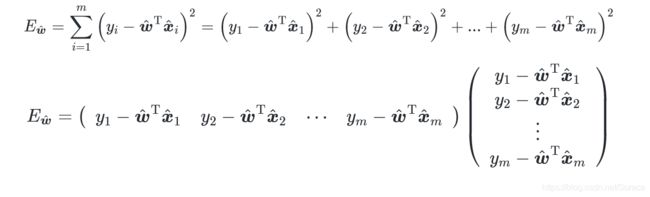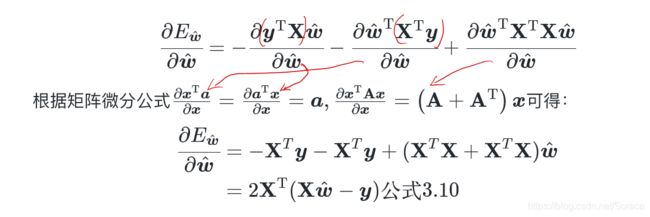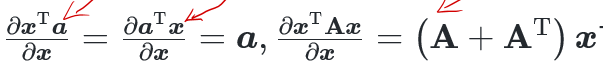Datawhale7月“吃瓜教程”Task02打卡

ps:本文为记录参与Datawhale-7月吃瓜教程的学习笔记

pss:文章所有PPT截图来自于：Datawhale吃瓜教程（https://www.bilibili.com/video/BV1Mh411e7VU），记得一键三连~

目录

Task02 详读西瓜书+南瓜书第3章

1 线性回归

1.1 一元线性回归

1.2 多元线性回归

2 对数几率回归

3 线性判别分析

4 多分类学习

5 类别不平衡问题

---

Task02 详读西瓜书+南瓜书第3章

1 线性回归

基本形式：

优点： 形式简单，易于建模。

 ω 可以直观表达了各属性在预测中的重要性，因此线性模型有很好的‘可解释性’，如下图所示呈现了ω的部分取值特征。

1.1 一元线性回归

先假设输入的属性的数目只有一个，此时线性回归试图学得

,使得

 

几何角度：
 

性能度量：

（1）最小二乘估计：基于均方误差最小化来进行模型求解的方法。

其中表示w和b的解；arg min()是使得式子达到最小值的w,b；,是已知的。 

在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小.。

求解w和b

一些概念记录

凸集与凸函数：

梯度：

 海塞矩阵：

证明 是关于w和b的凸函数 先证明海塞矩阵在D上是半正定的。

 证明求出的是最小值点。

公式（3.5）~（3.8）的推导过程：

 

 

 

 

（2）极大似然估计

 

 例题：

 对数似然函数：

证明在线性回归中，极大似然估计与最小二乘估计”殊途同归“

 

 将向量化的原因：想将下式用Python来实现的话，其中的求和公式需要用循环来实现，但是如果将其转换为向量的形式，就可以使用Python中的NumPy库来加速矩阵的运算。

 上式向量化：

 

 

 其中，

 

 机器学习三要素

1.2 多元线性回归

考虑更一般的情形即数据集D的样本由d个属性来描述。此时线性回归试图学到：

 ,使得

 

 

向量化 :

 

 

 

求解 :

 

 

 

 

 当为吗，满秩矩阵或正定矩阵时，

 

 矩阵微分公式：

 

 

2 对数几率回归

对数几率回归本质上是个分类算法，其在线性模型的基础上套一个映射函数来实现分类功能。

优点：可以直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确所带来的问题；可以得到近似概率预测，对许多需利用概率辅助决策的任务很有用；对率函数是任意阶可导的凸函数，许多数值优化算法可直接用于求取最优解。

线性回归模型简写为：

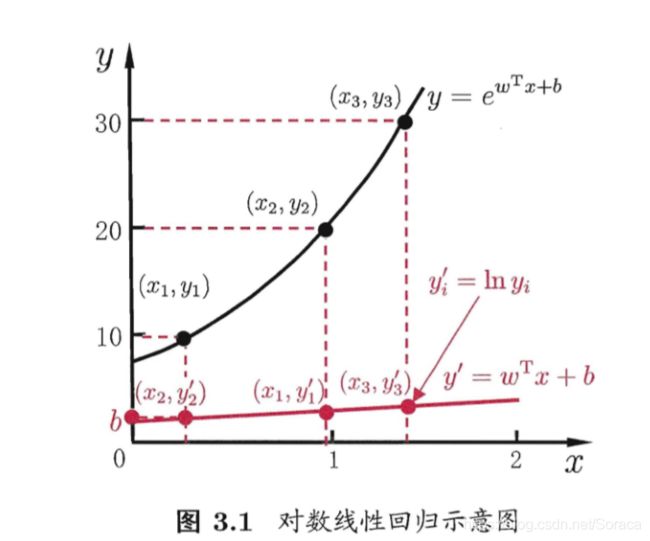
其对数线性回归为：

它试图让逼近y，对数函数能将线性回归模型的预测值与真实标记(如0,1）联系起来.

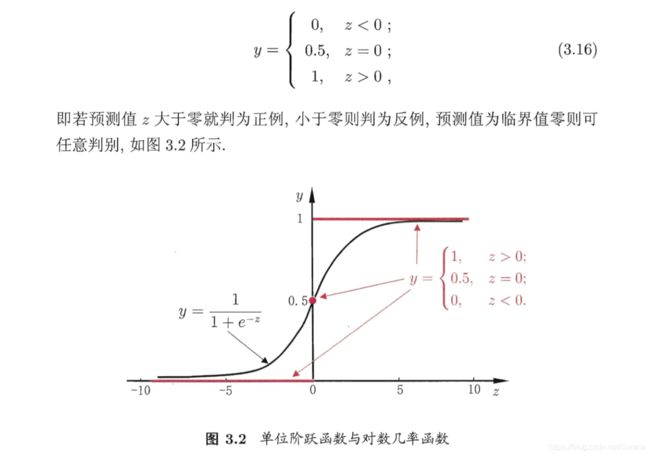
举个具体的例子：单位阶跃函数在二分类任务中的表现为：

 

 

对数几率回归也常称为逻辑回归，其表达式为

 

 可变化为

 用极大似然法来估计w和b：

 

 

 

 

 然后可以根据凸优化理论的经典数值优化算法如如梯度下降法(gradient descent method)、牛顿法(Newton method)等都可求得其最优解。

梯度下降法和牛顿法具体思想尚未了解，待补充........

3 线性判别分析

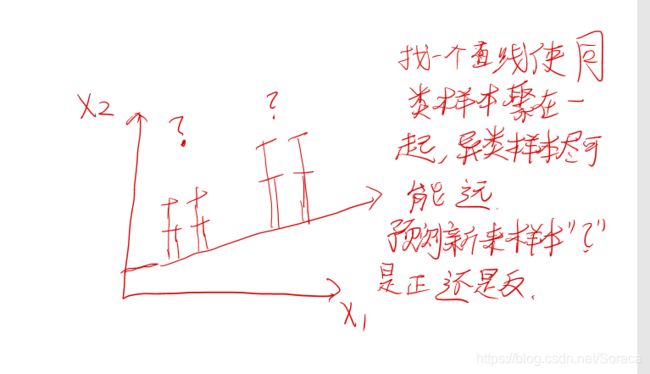
线性判别分析（Linear Discriminant Analysis,LDA）的基本思想是给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

几何思想：

自己画的：

 书上的：

 算法原理：

 损失函数推导：

 

 

 求解:

 补充拉格朗日乘子法：

 其中极值点不一定是最值点，可能仅是局部最优解，算出极值点后还需带回原函数来比较得出最优解。

 接上：

 

 补充广义特征值和广义瑞利商：

 

 

 LDA可应用于多分类任务中，其中一种常见实现是采用优化目标：

 根据交流群的补充说明为什么W是N-1维？

新样本必须分到一个类中，那么如果都不属于其他类就只剩下最后一个类。如做二分类任务，其实只需要分一次类即可。

4 多分类学习

多分类问题的话，可以拆解成多个二分类，那么拆解的方法就有一对一(One vs. One,OvO)、一对余(One vs. Rest,OvR)，多对多(Many vs. Many ,MvM)。

1.OvO

将N个类别两两配对,可以拆分N ( N − 1 ) / 2 个二分类的任务，得到N ( N − 1 ) / 2个分类结果，最终结果可以通过投票产生。

2.OvR
如果是一对余，那就把一个类的样例当正例，其他类放在一起算做反例。产生N 个二分类的任务。在测试时，若仅有一个分类器预测为正类，则对应类别标记为最终分类结果；若多个分类器预测为正类，通常考虑各个分类器的预测置信度，选置信度最大的类别标记作为分类结果。

 3.MvM

每次将若干个类作为正类，其他若干类作为反类。

MvM最常用的技术：”纠错输出码“(Error Correcting Output Codes,ECOC)。

5 类别不平衡问题

类别不平衡(class-imbalance)就是指分类任务中不同类别的训练样例数目差别很大的情况。例如有998个反例，但正例只有2个，那么学习方法只需返回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度;然而这样的学习器往往没有价值，因为它不能预测出任何正例。

用来举例，我们用该式子对新样本x进行分类时，实际上时再用预测的y值与一个阈值进行比较，在y>0.5时判定为正例，否则为反例，y实际上表达了正例的可能性，而反映了正例可能性与反例可能性之比，此时阈值设定为0.5，代表分类器认为真实的正反例的可能性相同，即分类器决策规则为时，预测为正例。

考虑更一般的情形，当训练集中正例数目(m+)、反例数目(m−)，两者不同时，观测几率是m+/m−，若,则预测为正例。又由于通常我们假设训练集是真实样本总体的无偏采样，因此观测几率就代表了真实几率。但事实上这个假设往往并不成立，也就是说我们未必能有效地基于训练集观测几率来推断出真实几率，为此现在以技术上说有三类解决策略：

1. 欠采样（undersampling）
2. 过采样（oversampling）
3. 阈值移动（threadhold-moving）

太菜了只能照着视频讲解的ppt才能看懂大部分所以没啥自己的输出多数是ppt截图，后续打算继续回看本章。

 ！！！！！！！！！！！！强烈推荐！！！！！！！！！！！！！！！

Datawhale吃瓜教程（https://www.bilibili.com/video/BV1Mh411e7VU）&&其组织所著的南瓜书（在线阅读地址：https://datawhalechina.github.io/pumpkin-book）