pytorch深度学习实战lesson22

第二十二课 LeNet 

    LeNet神经网络由深度学习三巨头之一的Yan LeCun提出，他同时也是卷积神经网络 (CNN，Convolutional Neural Networks)之父。

    LeNet主要用来进行手写字符的识别与分类，并在美国的银行中投入了使用。LeNet的实现确立了CNN的结构，现在神经网络中的许多内容在LeNet的网络结构中都能看到，例如卷积层，Pooling层，ReLU层。虽然LeNet早在20世纪90年代就已经提出了，但由于当时缺乏大规模的训练数据，计算机硬件的性能也较低，因此LeNet神经网络在处理复杂问题时效果并不理想。虽然LeNet网络结构比较简单，但是刚好适合神经网络的入门学习。

目录

理论部分

实践部分

---

理论部分

       Lenet最早是用来处理手写数字识别用的，随之出名的是mnist数据集。

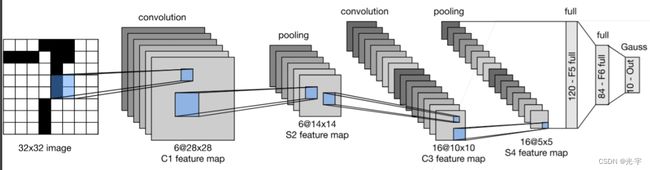
Lenet的具体结构：

       如图，LeNet-5（因为有5个卷积层而得名）是由卷积层、池化层、全连接层的顺序连接，网络中的每个层使用一个可微分的函数将激活数据从一层传递到另一层。LeNet-5开创性的利用卷积从直接图像中学习特征，在计算性能受限的当时能够节省很多计算量，同时也指出卷积层的使用可以保证图像的空间相关性（也是基于此，之后的一些网络开始慢慢摒弃全连接层，同时全连接层还会带来过拟合的风险）。

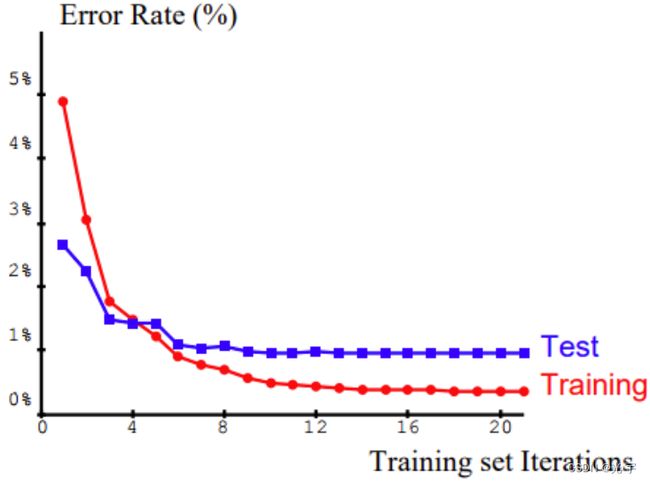
       此外，LeNet也是第一个成功的卷积神经网络应用，在当时主要用于识别数字和邮政编码，其用于手写数字识别的训练结果如图所示。

实践部分

代码：

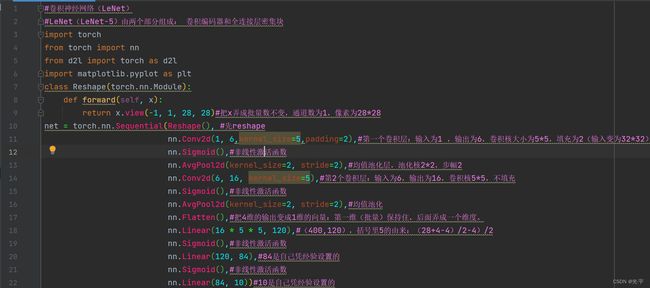
#卷积神经网络（LeNet）
#LeNet（LeNet-5）由两个部分组成： 卷积编码器和全连接层密集块
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
class Reshape(torch.nn.Module):
    def forward(self, x):
        return x.view(-1, 1, 28, 28)#把x弄成批量数不变，通道数为1，像素为28*28
net = torch.nn.Sequential(Reshape(), #先reshape
                          nn.Conv2d(1, 6,kernel_size=5,padding=2),#第一个卷积层：输入为1 ，输出为6，卷积核大小为5*5，填充为2（输入变为32*32）
                          nn.Sigmoid(),#非线性激活函数
                          nn.AvgPool2d(kernel_size=2, stride=2),#均值池化层，池化核2*2，步幅2
                          nn.Conv2d(6, 16, kernel_size=5),#第2个卷积层：输入为6，输出为16，卷积核5*5，不填充
                          nn.Sigmoid(),#非线性激活函数
                          nn.AvgPool2d(kernel_size=2, stride=2),#均值池化
                          nn.Flatten(),#把4维的输出变成1维的向量：第一维（批量）保持住，后面弄成一个维度。
                          nn.Linear(16 * 5 * 5, 120),#（400,120），括号里5的由来：（28+4-4）/2-4）/2
                          nn.Sigmoid(),#非线性激活函数
                          nn.Linear(120, 84),#84是自己凭经验设置的
                          nn.Sigmoid(),#非线性激活函数
                          nn.Linear(84, 10))#10是自己凭经验设置的
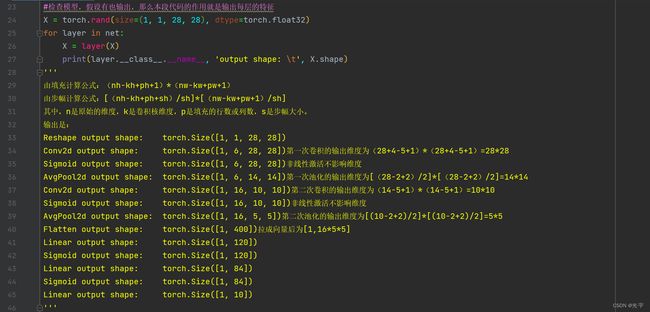
#检查模型，假设有也输出，那么本段代码的作用就是输出每层的特征
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape: \t', X.shape)
'''
由填充计算公式：（nh-kh+ph+1）*（nw-kw+pw+1）
由步幅计算公式：[（nh-kh+ph+sh）/sh]*[（nw-kw+pw+1）/sh]
其中，n是原始的维度，k是卷积核维度，p是填充的行数或列数，s是步幅大小。
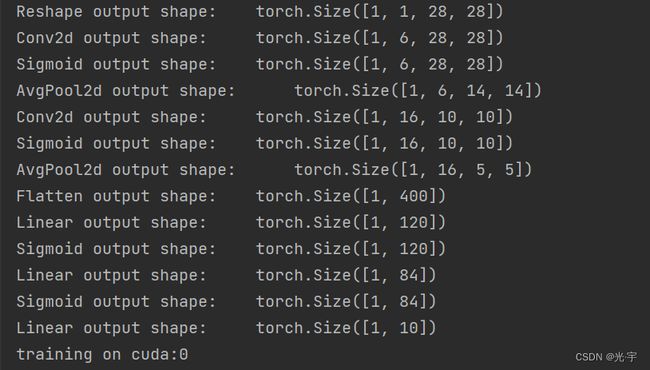
输出是：
Reshape output shape: 	 torch.Size([1, 1, 28, 28])
Conv2d output shape: 	 torch.Size([1, 6, 28, 28])第一次卷积的输出维度为（28+4-5+1）*（28+4-5+1）=28*28
Sigmoid output shape: 	 torch.Size([1, 6, 28, 28])非线性激活不影响维度
AvgPool2d output shape:  torch.Size([1, 6, 14, 14])第一次池化的输出维度为[（28-2+2）/2]*[（28-2+2）/2]=14*14
Conv2d output shape: 	 torch.Size([1, 16, 10, 10])第二次卷积的输出维度为（14-5+1）*（14-5+1）=10*10
Sigmoid output shape: 	 torch.Size([1, 16, 10, 10])非线性激活不影响维度
AvgPool2d output shape:  torch.Size([1, 16, 5, 5])第二次池化的输出维度为[(10-2+2)/2]*[(10-2+2)/2]=5*5
Flatten output shape: 	 torch.Size([1, 400])拉成向量后为[1,16*5*5]
Linear output shape: 	 torch.Size([1, 120])
Sigmoid output shape: 	 torch.Size([1, 120])
Linear output shape: 	 torch.Size([1, 84])
Sigmoid output shape: 	 torch.Size([1, 84])
Linear output shape: 	 torch.Size([1, 10])
'''
#LeNet在Fashion-MNIST数据集上的表现
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)#加载数据集
#对 evaluate_accuracy函数进行轻微的修改
def evaluate_accuracy_gpu(net, data_iter, device=None):
    """使用GPU计算模型在数据集上的精度。"""
    if isinstance(net, torch.nn.Module):#如果使用torch。nn的版本
        net.eval()#会变成评估模式
        if not device:#如果没指定设备的话
            device = next(iter(net.parameters())).device#就把第一个network（网络层）的device拿出来用
    metric = d2l.Accumulator(2)#累加器
    for X, y in data_iter:#对每一个xy
        if isinstance(X, list):#如果是torch.nn模式的话就让每一个xy都应用torch.nn使用的device
            X = [x.to(device) for x in X]
        else:#反之
            X = X.to(device)#就让每一个xy使用第一个网络层的device，意思就是都统一使用第一个网络层的device
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())#所有Y的个数
    return metric[0] / metric[1]#分类正确的个数除总数得到正确率
#为了使用 GPU，我们还需要一点小改动
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)。"""
    def init_weights(m):#初始化权重
        if type(m) == nn.Linear or type(m) == nn.Conv2d:#如果是线性层或卷积层
            nn.init.xavier_uniform_(m.weight)#就用定义好的初始化函数，根据输入输出大小，当进行随机初始化的时候，方差之类的数据差不多，
                                             #防止模型一开始梯度爆炸或梯度清零。
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
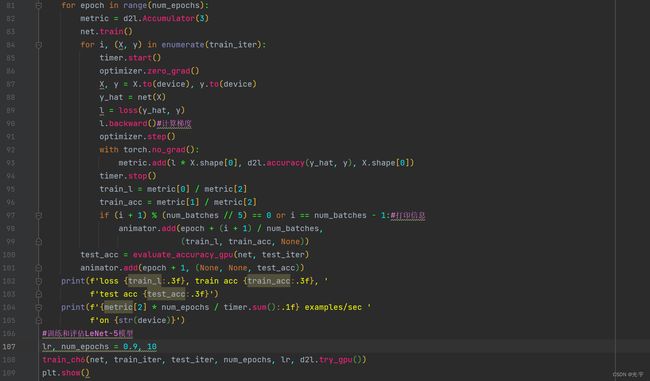
    for epoch in range(num_epochs):
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()#计算梯度
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:#打印信息
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
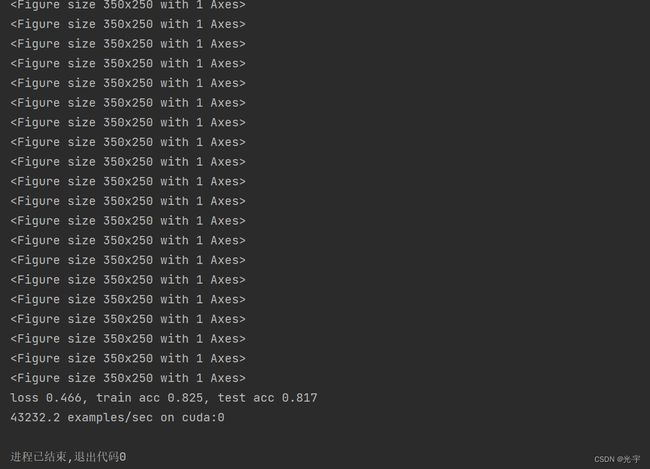
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')
#训练和评估LeNet-5模型
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()

Reshape output shape:      torch.Size([1, 1, 28, 28])
Conv2d output shape:      torch.Size([1, 6, 28, 28])
Sigmoid output shape:      torch.Size([1, 6, 28, 28])
AvgPool2d output shape:      torch.Size([1, 6, 14, 14])
Conv2d output shape:      torch.Size([1, 16, 10, 10])
Sigmoid output shape:      torch.Size([1, 16, 10, 10])
AvgPool2d output shape:      torch.Size([1, 16, 5, 5])
Flatten output shape:      torch.Size([1, 400])
Linear output shape:      torch.Size([1, 120])
Sigmoid output shape:      torch.Size([1, 120])
Linear output shape:      torch.Size([1, 84])
Sigmoid output shape:      torch.Size([1, 84])
Linear output shape:      torch.Size([1, 10])
training on cuda:0

*100
loss 0.466, train acc 0.825, test acc 0.817
43232.2 examples/sec on cuda:0

进程已结束,退出代码0