2022-01-24 每日打卡：周赛总结

2022-01-24 每日打卡：周赛总结

写在前面

“这些事儿在熟练之后，也许就像喝口水一样平淡，但却能给初学者带来巨大的快乐，我一直觉得，能否始终保持如初学者般的热情、专注，决定了在做某件事时能走多远，能做多好。” 该系列文章由python编写，所刷题目共三个来源：之前没做出来的 ；Leetcode中等，困难难度题目； 周赛题目；某个专题的经典题目，所有代码已AC。每日1-3道，随缘剖析，希望风雨无阻，作为勉励自己坚持刷题的记录。

周赛总结

最近两场周赛，比较明显的进步是最后一题偶尔也能做出来了，但是前面的题对于一次过的要求还是达不到，某些细节上的使用不能一步到位。
总结一下在提交之前需要检查：用例，题目信息，边界（特殊情况），重复样例。

2146. 价格范围内最高排名的 K 样物品（第 70 场双周赛T3）

广度搜索即可，只要是能走到的格子，一定被加入队列，所以广度搜索一定可以搜遍全部的格子，将符合条件的加入，不符合条件的去掉就可以了。

class Solution:
    def highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:
        N = len(grid)
        M = len(grid[0])
        low, high = pricing
        row, col = start
        visited = [[False] * M for _ in range(N)]
        if grid[row][col] == 0:
            return []
        visited[row][col] = True
        all_pos = []
        # 使用队列进行广度搜索
        q = [(row, col, 0)]
        f = 0
        while f < len(q):
            x, y, d = q[f]
            f += 1
            if low <= grid[x][y] <= high:
                all_pos.append((d, grid[x][y], x, y))
            # 对上下左右四个方向的搜索
            for dx, dy in ((-1, 0), (1, 0), (0, 1), (0, -1)):
                if 0 <= x + dx < N and 0 <= y + dy < M and not visited[x + dx][y + dy]\
                        and grid[x + dx][y + dy]:
                    visited[x + dx][y + dy] = True
                    q.append((x + dx, y + dy, d + 1))
        all_pos.sort()
        return [[x, y] for _, _, x, y in all_pos[:k]]
        

2151. 基于陈述统计最多好人数（第 277 场周赛T4）

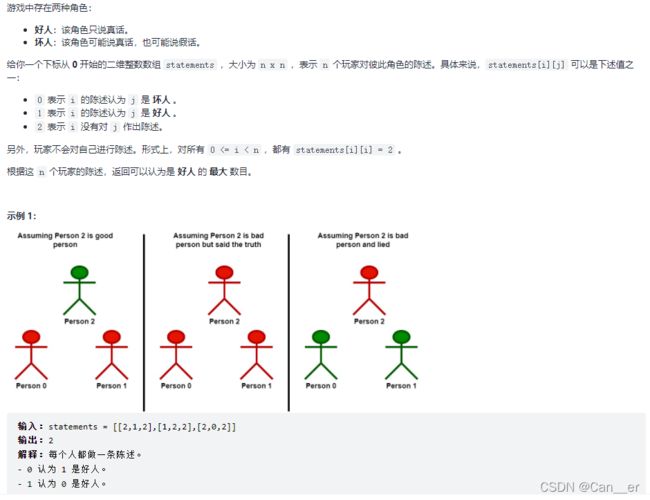
比赛的时候以为是dfs+博弈论，就像是翻转灯泡那样的，结果一直没找到【可以枚举出的】初始状态。在看题解的时候发现了一句很重要的话：由于本题中 $n\le 15$，因此我们可以使用 $O(2^n)$ 的时间枚举每一种情况：即每个人是好人或坏人有 2种情况，一共有 n 个人。
一方面可以看出平时自己不太重视的【数据范围】的重要性，另一方面可以看出【结果为1或0】往往是对位运算+枚举的暗示。

class Solution:
    def maximumGood(self, statements: List[List[int]]) -> int:
        def check():
            for i in range(cnt):
                for j in range(cnt):
                    if statements[i][j]==0 and mask &(1<<i) and mask & (1<<j):
                        return False
                    elif statements[i][j]==1 and mask &(1<<i) and not mask &(1<<j):
                        return False
            return True
        ans, cnt = 0, len(statements)
        # 正好需要枚举 0 ~ 2^(cnt)-1 共2^cnt位
        for mask in range(0, 1<<cnt):
            if check():
                ans = max(ans,bin(mask).count(1))
        return ans