Matlab学习笔记——fitlm
fitlm使用笔记
参考matlab文档及《数学建模算法与应用》第三版回归分析部分matlab代码的学习笔记。仅用于保存个人笔记学习使用参考。
文章目录
- fitlm使用笔记
- fitlm基本用法
-
- 基本操作:fitlm(X, Y)
- 输出图像
- 虚拟变量的建立
- 使用项矩阵拟合的回归模型(交互项)
- 具有分类的预测变量
-
- fitlm默认分类
- 手动分类
- 为线性模型指定响应变量和预测变量
- 稳健线性回归模型拟合
fitlm基本用法
基本操作:fitlm(X, Y)
代码
%% 导入数据
load carsmall % 导入matlab自带数据
X = [Weight,Horsepower,Acceleration]; % 自变量
Y = MPG; % 因变量
md1 = fitlm(X, Y)
plot(md1)
% md1.Coefficients
- 线性回归模型:y = β0 + β1 x1 + β2 x2 + β3 x2
- 估计系数:为table数据类型表格,通过md1.Coefficients调用。
- Estimate:从上到下分别为常系数,自变量x的系数。
- SE: 系数的标准误差
- tStat:每个系数的t统计量
- pValue:每个系数对应的p值
*注. t统计量为t检验的结果,当t < ta时该系数显著。ta通过matlab函数tinv求得,其用法:
ta = tinv(1 - alpha/2, n - m - 1) % alpha通常为0.05,n为样本点个数,m为自变量个数
- 模型输出的结果中最后的文字为对模型的评估,包括相关系数等。其中F值于p值为对模型的显著性检验,F > Fa则模型显著,Fa的matlab函数为
Fa = finv(1 - alpha, m, n - m - 1)
输出图像
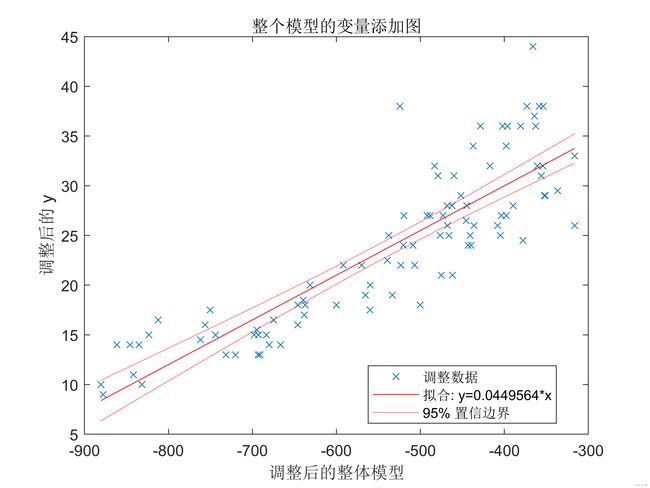
plot(md1)
虚拟变量的建立
% tbl表示建立table表格类型数据。
tbl = table(Weight ,Horsepower, Acceleration, MPG, 'VariableNames',...
{'Weight','Horsepower','Acceleration','MPG'});
% 对tbl中的数据进行建模,后面跟着的是回归方程样式
lm = fitlm(tbl,'MPG~Weight+Horsepower+Acceleration')
使用项矩阵拟合的回归模型(交互项)
代码:
T = [0 0 0; 1 0 0; 0 1 0; 1 1 0; 0 2 0];% 项矩阵
X = [Acceleration,Weight]; % 输入变量
Y = MPG; % 响应变量
md2 = fitlm(X, Y, T)
项矩阵T的理解:
从矩阵T的列来看,第一列代表x1, 第二列代表x2,第三列代表响应变量。注意,matlab中为做指定的情况下默认最后一列为响应变量,且响应变量在项矩阵T中为0列。
从矩阵的内容来看,由于第三列为响应变量列全为0我们不做讨论,其余列分别对x1, x2进行描述。0 0 0表示常系数;1 0 0表示x1的一次幂;0 2 0表示x2的二次幂;1 1 0表示x1于x2的一次幂且二者为交互关系(x1*x2)
输出结果

具有分类的预测变量
fitlm默认分类
代码
mdl = fitlm(Model_Year,MPG,'CategoricalVars',1,...
'VarNames',{'Model_Year','MPG'})
输出
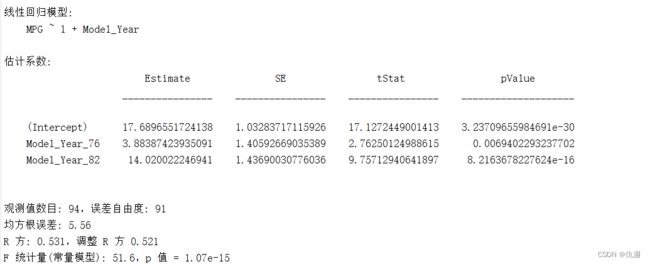
解释
1.如果 Model_Year 的值分别为 76 和 82,则其值为 1。Model_Year包含70,76,82。这里fitlm是基于最小值70作为参考水平创建的指示变量。
手动分类
代码
temp_Year = dummyvar(categorical(Model_Year));
% categorical:将Model_Year这个table类型的表格数据转换为数组数据
% dummyvar:将数组数据中的唯一值转换为逻辑矩阵表达
Model_Year_70 = temp_Year(:,1);
Model_Year_76 = temp_Year(:,2);
Model_Year_82 = temp_Year(:,3);
tbl = table(Model_Year_70,Model_Year_76,Model_Year_82,MPG);
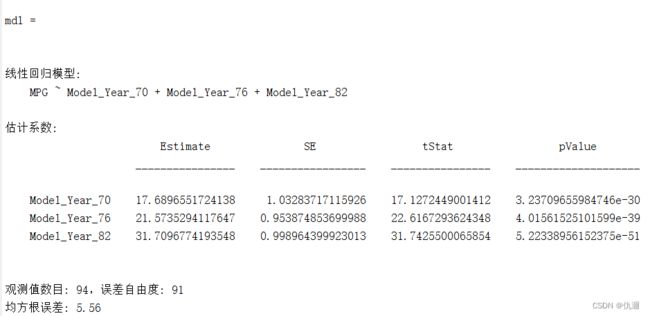
mdl = fitlm(tbl,'MPG ~ Model_Year_70 + Model_Year_76 + Model_Year_82 - 1')
为线性模型指定响应变量和预测变量
代码
load hospital % 导入数据
mdl = fitlm(hospital,'interactions','ResponseVar','Weight',...
'PredictorVars',{'Sex','Age','Smoker'},...
'CategoricalVar',{'Sex','Smoker'})
解释
‘interactions’:表示具有交互项
‘ResponseVar’:后面跟着的table列名为响应变量名
‘PredictorVars’:后面跟着的table列名为预测变量名
‘CategoricalVar’:后面跟着的table列名为分类变量名
输出

稳健线性回归模型拟合
代码:
md1 = fitlm(X, Y, 'RobustOpts', 'on')
说明
稳健线性回归是不同于最小二乘回归的一种回归算法,相比于最小二乘回归其具有更高的容错性。在这里不做具体分析,本科数学建模竞赛中通常使用最小二乘回归足矣,若有需要可参考其他文献。
仅用于保存个人笔记学习使用参考。