机器学习6：决策树相关的概念

先补充一个物理概念

熵

Entropy: 度量事物的不确定性，不确定性越高，熵就越大，反之越确定，熵越小；

随机事件(多类别)的熵可以表示为：

$$entropy=-p_{1}lo{g}_2(p1)-p_{2}lo{g}_2(p2)-...-p_{n}lo{g}_2(p_n)=-\sum _{i=1}^n{p}_{i}lo{g}_2(p_i)$$

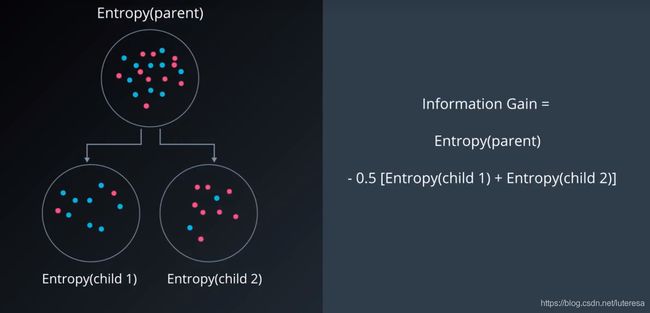
信息增益：

父结点的熵与子结点上的平均值之间的差值；

1.决策树算法原理：

信息增益最大化: 每步决策都选择信息增益最大的特征，作为当前分类特征依据

import numpy as np
def two_group_ent(first, tot):                        
    return -(first/tot*np.log2(first/tot) + (tot-first)/tot*np.log2((tot-first)/tot))

tot_ent = two_group_ent(10, 24)                       
g_feature_17_ent = 15/24 * two_group_ent(11,15) + 9/24 * two_group_ent(6,9)                  

answer = tot_ent - g17_ent  

print(answer)

0.11260735516748954

2.决策树的超参数

为了创建泛化能力好的决策树，我们可以调优决策树的多个方面。我们把决策树的这些可调优的多个方面称为“超参数”。以下是决策树中使用的一些最重要的超参数。

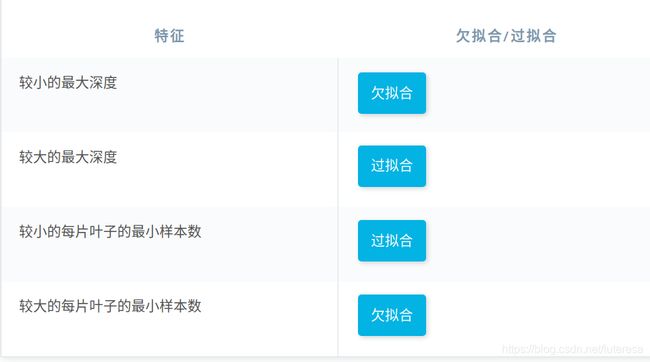
2.1最大深度

决策树的最大深度就是从根到叶之间可能的最大长度。一个最大深度为 k 的决策树最多有$2^k$ 个叶子。

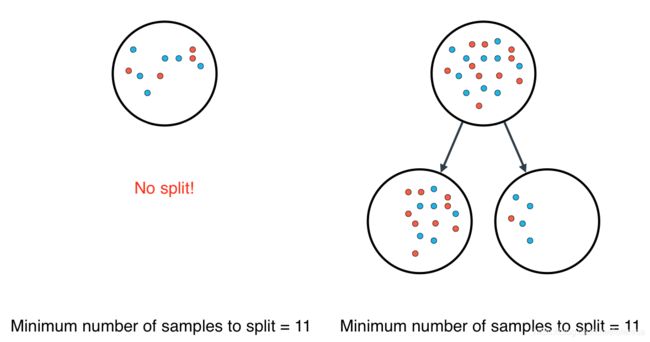
2.2最少样本分割数

一个节点必须至少有min_samples_split个样本才能足够大以进行拆分。如果一个节点的样本数少于 min_samples_split 个， 则分割过程停止，该节点不会被分割。

然而 min_samples_split 不会控制叶的最小尺寸。正如你在上面右边的示例中看到的，父节点有20个样本，大于min_samples_split = 11，因此这个节点被拆分。但在此节点被拆分后，有一个子节点的样本数为5，小于min_samples_split = 11。

2.3每片叶子的最小样本数

当分割一个节点时，可能会遇到的一个问题是分割不均匀，例如某个子节点有99个样本，另一个子节点可能只有1个样本。这会影响决策树的生成，也浪费计算资源和时间。为避免这种情况，我们可以为每个叶子上允许的样本数设置一个最小值。

2.4每次分裂的最小样本数

这个参数与每片叶子上的最小样本树相同，只不过是应用在节点的分裂当中。

2.5最大特征数

有时，我们会遇到特征数量过于庞大，而无法建立决策树的情况。在这种状况下，对于每一个分裂，我们都需要检查整个数据集中的每一个特征。这种过程极为繁琐。而解决方案之一是限制每个分裂中查找的特征数。如果这个数字足够庞大，我们很有可能在查找的特征中找到良好特征（尽管也许并不是完美特征）。然而，如果这个数字小于特征数，这将极大加快我们的计算速度。

3.sklearn 中的决策树

对于决策树模型，你将使用 scikit-learn 的 Decision Tree Classifier 类。该类提供了定义模型并将模型与数据进行拟合的函数。

from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
model.fit(x_values, y_values)
print(model.predict([ [0.2, 0.8], [0.5, 0.4] ]))

可设置超参数

当我们定义模型时，可以指定超参数。在实践中，最常见的超参数包括：

max_depth：树中的最大层级数量。

min_samples_leaf：叶子允许的最低样本数量。

min_samples_split：拆分内部节点所需的最低样本数量。

max_features：寻找最佳拆分方法时要考虑的特征数量。

例如，在此例中，我们定义了一个模型：树的最大深度 max_depth 为7，每个叶子的最低元素数量 min_samples_leaf 是 10。

model = DecisionTreeClassifier(max_depth = 7, min_samples_leaf = 10)

构建决策树步骤：

1.构建决策树模型

使用 scikit-learn 的 DecisionTree 类构建决策树分类模型，并将其赋值给变量 model。

2.将模型与数据进行拟合

你不需要指定任何超参数，因为默认的超参数将以 100% 的准确率拟合数据。

但是，建议你实验这些超参数，例如 max_depth 和 min_samples_leaf，并尝试找到最简单的潜在模型，即最不太可能过拟合的模型！

3.使用模型进行预测

预测训练集的标签，并将此列表赋值给变量 y_pred。

4.计算模型的准确率

为此，使用 sklearn 函数 accuracy_score。

代码实现:

# Import statements 
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import pandas as pd
import numpy as np

# Read the data.
data = np.asarray(pd.read_csv('data.csv', header=None))
# Assign the features to the variable X, and the labels to the variable y. 
X = data[:,0:2]
y = data[:,2]

# TODO: Create the decision tree model and assign it to the variable model.
# You won't need to, but if you'd like, play with hyperparameters such
# as max_depth and min_samples_leaf and see what they do to the decision
# boundary.
model = DecisionTreeClassifier()

# TODO: Fit the model.
model.fit(X,y)
# TODO: Make predictions. Store them in the variable y_pred.
y_pred = model.predict(X)

# TODO: Calculate the accuracy and assign it to the variable acc.
acc = accuracy_score(y_pred, y)

print(acc)

1.0

小结：

决策树的一个重要任务是为了理解数据中所蕴含的知识信息，因此决策树可以使用不熟悉的数据集合，并从中提取一系列规则。

这个机器根据数据集创建规则的过程，就是机器学习过程。

专家系统中，经常使用决策树，而且决策树给出结果往往可以匹配当前领域具有几十年工作经验的人类专家。

优点：计算复杂度不高，输出结果易于理解，对中间值的却是不敏感，可以处理不相关特征数据；

缺点：可能会产生过度匹配问题；

适用数据类型：数值型和标称型。