深度学习入门之激活函数
深度学习入门之激活函数
参考书籍:深度学习入门——基于pyhthon的理论与实现
文章目录
- 深度学习入门之激活函数
- 前言
- 一、sigmoid函数
-
- 1.简介
- 2.python实现
- 3.函数用法
- 二、阶跃函数
-
- 1.简介
- 2.python实现阶跃函数
- 3.函数用法
- 三、ReLU函数
- 1.简介
- 2.python实行ReLU函数
- 总结
前言
将输入信号的总和转换为输出信号,这种函数一般称为激活函数(activation function)。激活函数作用在于决定如何来激活输入信号的总和。激活函数作为感知机和神经网络的桥梁。它的出现使得输出从单一变为数值化。激活函数以阈值为界,一旦输入超过阈值,就切换输出,这样的函数称为‘阶跃函数’。因此,可以说感知机中使用了阶跃函数作为激活函数。接下来,简单介绍一下激活函数的种类。
一、sigmoid函数
1.简介
神经网络中第一个激活函数就是S型生长曲线,也就是sigmoid函数(sigmoid function),它的数学表达式如下:
h ( x ) = 1 1 + e x p ( − x ) h(x)=\frac {1} {1+exp(-x)} h(x)=1+exp(−x)1
其中,exp(-x)表示的是e^(-x),e为纳皮尔常数2.7182…,尽管从函数表达式上来看激活函数,显得比较复杂,但是我们从另一个角度去解读,就可以认为:给定一个输入后,经过此函数运算可以得到某个输出的转换器。比如,向sigmoid函数输入1.0或者2.0后,就会有某个值被输出,类似:
h ( 0.1 ) = 0.731 ⋯ h ( 0.2 ) = 0.880 ⋯ h(0.1)=0.731\cdots \\ h(0.2)=0.880\cdots h(0.1)=0.731⋯h(0.2)=0.880⋯
2.python实现
下面,利用python来实行sigmoid函数,代码如下:
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
这里,注意的是参数x为numpy数组,结果也能被正确计算,实际运用中,sigmoid函数的输入参数实际就是一个numpy数组,实验结果如下:
>>> x = np.array([-1.0 , 1.0 , 2.0])
>>>sigmoid(x)
>array([0.2689142,0.73105858 0.88079708])
sigmoid函数的图形,关于x=0对称,值域在[0,1]之间,整个形状呈现’S’型,因此也称其为S型生长曲线,sigmoid函数的曲线图形如下:
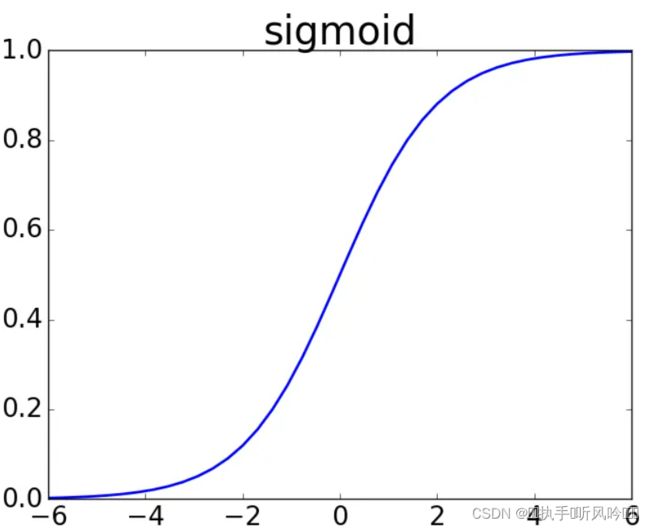
3.函数用法
神经网络中,用sigmoid函数作为激活函数,进行信号的转换,转换后的信号被传送给下一个神经元。实际上,感知机和神经网络的最主要区别就在于这个激活函数,其他方面,比如神经网络的多层连接的构造、信号的传递方法等,基本上和感知机是一样的。
二、阶跃函数
1.简介
阶跃函数相当于sigmoid函数来说,较为简单,阶跃函数在x=0有一个突变过程,数学表达式如下:
h ( x ) = { 0 ( x < 0 ) 1 ( x ⩾ 0 ) h(x) = \begin{cases} 0& (x<0)\\1&(x \geqslant 0) \end{cases} h(x)={01(x<0)(x⩾0)
阶跃函数从其数学表达式就可以看出:当输入信号超过0时,输出为1,否则输出为0。
2.python实现阶跃函数
python实现阶跃函数还是非常简单的,只需要一个判断即可。
代码如下(示例):
import numpy as np
def step_function(x):
if x >0:
return 1
else
return 0
这个形式的实现确实比较简单,但是这个函数存在一定的不足,因为这个函数的输入参数x只能接收实数数据,即浮点数,例如step_function(3.0)的调用,不允许参数取numpy数组,例如step_function(np.array([1.0 ,2.0]))的调用,所以为了满足numpy数组的调用,所以需要对程序进行修改,为什么需要满足numpy数组呢?这是因为后面的数据不可能单一的出现,而是一个数据组的出现,就如图片数据。
将程序修改成为numpy数组支持的形式:
import numpy as np
def step_function(x):
y = x > 0
return y.astype(np.int)
该函数中,y的输出是一个bool值得numpy数组,判断x和0的大小,根据大小,输出bool值,x大于0时,y输出True,否则y输出False,y的dtype=bool。
但是,函数输出需要的是一个int型的数据,即需要0或者1的输出,所以,在数据返回时,利用astype()方法转换numpy数组的数据类型。astype通过指定的参数,达到转换为指定的数据类型,astype(np.int),就是将y中的bool数组转换为0、1的int数组,true会转换为1,false会转换为0。
阶跃函数的图形,比较像一个楼梯,在x=0处,发生突变,出现阶跃信号。图形如下所示:
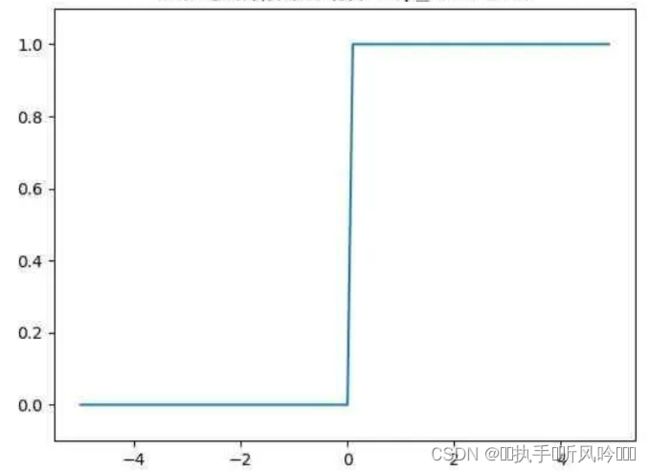
3.函数用法
阶跃函数以0为界,输出从0切换为1,或者说从1切换为0,它的值呈现阶梯式变化。相对比与sigmoid函数,阶跃函数的输出发生更加急剧性变化,而sigmoid函数的变化更加平滑,sigmoid函数平滑性对神经网络的学习具有重要的意义,阶跃函数的输出急剧性,就像竹筒敲石头一般,输出变化只有两个状态就是敲与不敲,而sigmoid函数就像水车,根据流过来的水量做相应调整在输出。但是两者的作用是一致的,对重要信息会有较大输出,小信号会输出较小的值。
三、ReLU函数
1.简介
ReLU函数现在使用的比较多,该函数在大于0时,直接输出该值;在小于0时,输出直接为0.
ReLU函数的数学表述式如下所示:
h ( x ) = { x ( x > 0 ) 0 ( x ≧ 0 ) h(x)= \begin{cases} x &(x>0) \\0 & (x\geqq0) \end{cases} h(x)={x0(x>0)(x≧0)
ReLU函数也是一个比较简单的函数。
2.python实行ReLU函数
根据ReLU函数的数学公式,可以将程序写为:
import numpy as np
def relu(x):
return np.maximum(0,x)
这里使用了maximum函数对输入的信号和0进行比较,选择一个最大的输出,比如输入的x=12,relu函数则会输出12,如果输入x=-12,relu函数的输出就会变为0。
该例子只是简单实现,对于实际的神经网络运算比这个例子要更加复杂,但是不影响后面结论成立。
relu函数的图像,也可以通过它的数学表达可以直接表述出来,较好理解,图形如下所示:
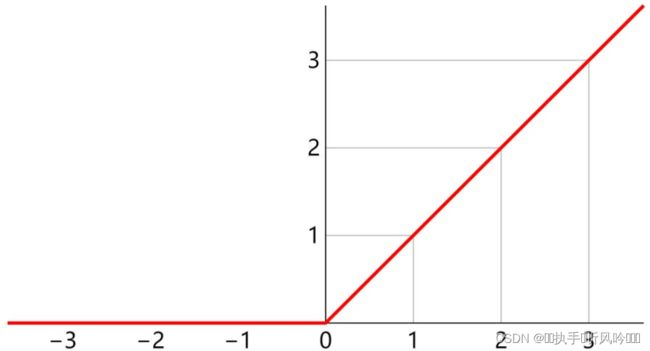
总结
本文仅仅简单介绍了激活函数的种类,主要讲述了sidmoid函数、阶跃函数、ReLU函数的数学表达式,python简单实现以上的激活函数,简单介绍了使用技巧。