python学习笔记 4 - 线性回归、波士顿房价数据分析

1 什么是机器学习？

给定一组(x(i), y(i))，给定一个模型，将x(i)输入模型后得到y(i)^
计算y(i)和y(i)^的差距，差距越小，模型越优。
通过不断地优化模型，使得差距越来越小，这就是机器学习

2 分类与回归

在上述例子中，y的值有可能是连续的，也有可能离散的。
离散的指的是y值之间没有大小关系。如打分1，2，3，4，5，虽然是数学意义上的离散，但是因为有大小关系，因此不是离散。
如果y的值是连续的，则是回归问题；如果y的值是离散的，则是分类问题。

3 过拟合与欠拟合

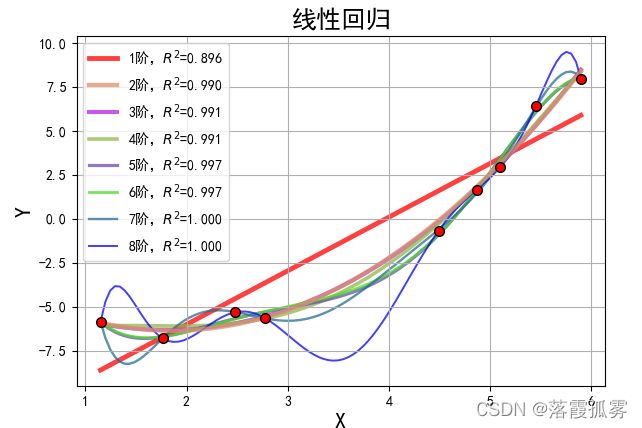
过拟合与欠拟合在图形上可以很容易看出来，图中1阶为欠拟合，8阶为过拟合，
而在数学表现上，可以看到图像上的参数如下：

1阶，系数为： [-12.12113792 3.05477422]
2阶，系数为： [-3.23812184 -3.36390661 0.90493645]
3阶，系数为： [-3.90207326 -2.61163034 0.66422328 0.02290431]
4阶，系数为： [-8.20599769 4.20778207 -2.85304163 0.73902338 -0.05008557]
5阶，系数为： [ 21.59733285 -54.12232017 38.43116219 -12.68651476 1.98134176 -0.11572371]
6阶，系数为： [ 14.73304785 -37.87317494 23.67462342 -6.07037979 0.42536833 0.06803132 -0.00859246]
7阶，系数为： [ 314.30344622 -827.89446924 857.33293186 -465.46543638 144.21883851 -25.67294678 2.44658612 -0.09675941]
8阶，系数为： [-1189.50149198 3643.69109456 -4647.92941149 3217.22814712 -1325.87384337 334.32869072 -50.57119119 4.21251817 -0.148521 ]

可以看到，1 - 4阶的参数比较正常，而后面几阶的参数绝对值非常大，参数绝对值大，那么x的值稍微有一点变化，则结果变化会非常大，也就是过拟合。

4 使用线性回归分析波士顿房价

4.1 导入数据

波士顿房价的数据集网上有，这里用的是.data格式的，大概形式如下：

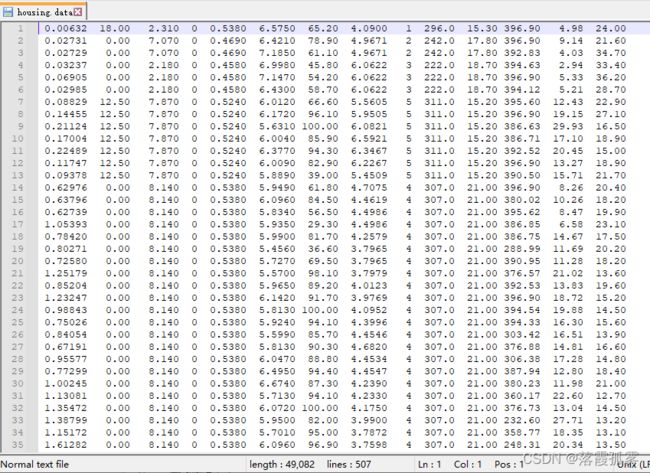
我们可以看到这里的数据不是csv或Excel格式，并且分隔不是用的’，’，而是用的tab（空格），并且每个数据间的空格数量不同。我们尝试使用之前的pd.read_csv读取数据，并用空格分隔数据：

import pandas as pd

if __name__ == '__main__':
    data = pd.read_csv('housing.data', sep=' ')
    print(data)

可以看到报错如下：

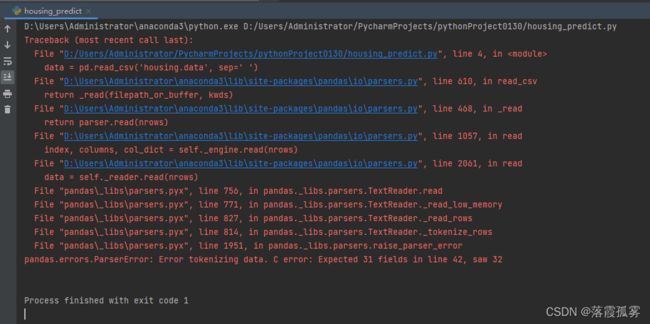
原因是分隔使用的空格，数量不相等，pandas无法使用空格将数据分开。
一个比较简单粗暴的修改方式是，使用替换功能，将数据中的所有连续两个空格替换成一个空格，重复多次后，数据的分隔就全部变成一个空格了。这种方式不太好，因为我们改变了原数据。
而另一个解决方式是使用正则表达式，
将第四行改成

    data = pd.read_csv('housing.data', sep='\s+', header=None)

这里的'\s+'就是使用的正则表达式，后面的header=None的意思是告诉pandas我们的数据没有数据头。
运行就可以得到我们的数据：

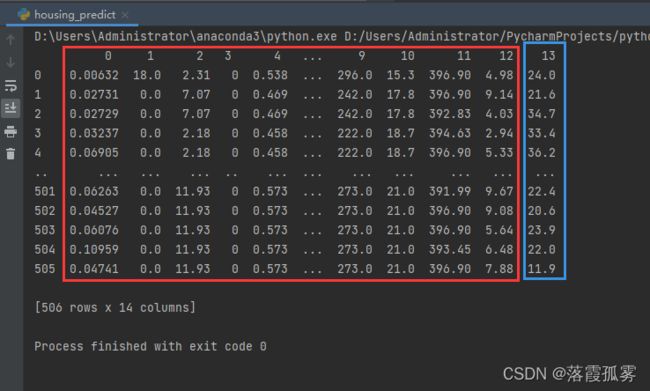
前面的0-12列就是我们的x，13列是y。
使用以下代码给x和y赋值：

    x,y = data.loc[:, :12], data.loc[:, 13] # loc的slice首尾都包括
    # x, y = data[np.arange(13)], data[13]

这样我们就把housing.data文件里的数据成功赋值给x和y了。

4.2 模型计算

使用from sklearn.linear_model import LinearRegression进行线性模型引入（未安装的话需要在cmd命令行输入pip install scikit-learn安装）。
输入如下代码：

    model = LinearRegression()  # 调用构造函数
    print(model)
    model.fit(x, y)
    print('系数：', model.coef_)
    print('截距：', model.intercept_)
    y_pred = model.predict(x)

代码第一行调用了LinearRegression中的构造函数，这里只是构造了，还没有给model喂数据，所以第二行打印的输出为LinearRegression()。
第三行将刚才获取到的x和y喂给模型，然后我们就可以得到模型的系数和截距。
最后一行的y_pred 就是我们通过模型得到的y的预测值。
我们可以使用print(np.mean((y-y_pred)**2))计算MSE
也可以通过导入包from sklearn.metrics import mean_squared_error, mean_absolute_error，使用系统提供的方法直接计算相关值。
使用如下代码：

    # print(np.mean((y - y_pred) ** 2))
    
    mse = mean_squared_error(y, y_pred)
    rmse = math.sqrt(mse)
    mae = mean_absolute_error(y, y_pred)

    print('MES = %.3f, RMSE = %.3f, MAE = %.3f' % (mse, rmse, mae))

这里有一个rmse，计算这个值的意义在于，我们计算的mse实际上是一个平方值，比如说我们的数据中y的单位为千元每平方，那么mse的单位就是（千元每平方）的平方，这样不直观也不好理解，因此我们这里对mse开方。

以上内容完整代码如下：

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error

if __name__ == '__main__':
    data = pd.read_csv('housing.data', sep='\s+', header=None)
    print(data)

    x,y = data.loc[:, :12], data.loc[:, 13] # loc的slice首尾都包括
    # x, y = data[np.arange(13)], data[13]
    print('X = ', x)
    print('Y = ', y)
    model = LinearRegression()  # 调用构造函数
    print(model)
    model.fit(x, y)
    print('系数：', model.coef_)
    print('截距：', model.intercept_)
    y_pred = model.predict(x)

    # print(np.mean((y - y_pred) ** 2))

    mse = mean_squared_error(y, y_pred)
    rmse = math.sqrt(mse)
    mae = mean_absolute_error(y, y_pred)

    print('MES = %.3f, RMSE = %.3f, MAE = %.3f' % (mse, rmse, mae))

4.3 划分训练集与测试集

在之前的例子中，我们把全部的506组数据都作为训练集对波士顿房价进行了学习，而在实际过程中，我们需要一部分数据作为训练集，一部分内容作为测试集。
我们采用的做法是，首先打乱数据集的顺序，然后选取前20%作为测试集，后80%作为训练集，代码如下：

    m, _ = data.shape   # 获取data的行数
    index = np.arange(m)
    print(index)
    np.random.shuffle(index)
    print(index)
    test_size = int(m*0.2)
    test_data = data.loc[index[:test_size], :]
    print(test_data)
    train_data = data.loc[index[test_size:], :]
    print(train_data)

这段代码首先获取了数据的行数，然后使用index作为每行数据的索引，使用np.random.shuffle(index)打乱index的顺序后，再选取index指向的数据中的前20%作为测试集，后80%作为训练集。

当然，sklearn包中也提供了直接供我们调用的方式来对数据集进行划分，导入包from sklearn.model_selection import train_test_split后，使用如下代码：

	x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

这句话的意思是将x按照测试集占总数据20%的比例进行划分，其中两部分的名称分别为x_train，x_test，y同。
这里要注意，使用train_test_split时，划分的结果的第一个是训练集，第二个是测试集。

划分好后，我们仍然用4.2提到的方式，将训练集喂给模型，之后用训练好的模型来预测测试集的结果，并进行比对。完整代码如下：

import math
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split

if __name__ == '__main__':
    np.set_printoptions(suppress=True)	# 强制输出格式为浮点数
    data = pd.read_csv('housing.data', sep='\s+', header=None)
    print(data)

    x,y = data.loc[:, :12], data.loc[:, 13] # loc的slice收尾都包括
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
    print(x_test, x_train)

    model = LinearRegression()  # 调用构造函数
    print(model)
    model.fit(x_train, y_train)
    print('训练集系数：', model.coef_)
    print('训练集截距：', model.intercept_)
    y_train_pred = model.predict(x_train)

    mse_train = mean_squared_error(y_train, y_train_pred)
    rmse_train = math.sqrt(mse_train)
    mae_train = mean_absolute_error(y_train, y_train_pred)

    print('训练集MSE = %.3f, RMSE = %.3f, MAE = %.3f' % (mse_train, rmse_train, mae_train))

    y_test_pred = model.predict(x_test)

    mse_test = mean_squared_error(y_test, y_test_pred)
    rmse_test = math.sqrt(mse_test)
    mae_test = mean_absolute_error(y_test, y_test_pred)

    print('测试集MSE = %.3f, RMSE = %.3f, MAE = %.3f' % (mse_test, rmse_test, mae_test))

在以上代码中，第19行使用了训练集对模型进行训练。
22行使用模型对训练集进行了预测；并在28行计算了训练集的MSE等值进行了输出。
30行使用模型对测试集的数据进行了预测，并在36行对使用该模型预测的结果与实际值进行了对比。

我的运行结果如下：

4.4 数据结果显示

在机器学习的过程中，我们不仅要看模型的学习结果，另一个我们想了解的内容还包括了模型最终的系数分别对应的值，以及这些值中，哪些更重要，对结果的影响更大。
因此我们在刚才的代码中，在一开始的读取data的部分，可以添加一些代码来将每个属性的名称显示出来。
将开头读取数据的代码做如下更改：

    np.set_printoptions(suppress=True)
    pd.set_option('display.width', 1000)
    pd.set_option('display.max_columns', 30)
    col_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
    data = pd.read_csv('housing.data', sep='\s+', header=None, names = col_names)
    print(data)

打印结果如图：

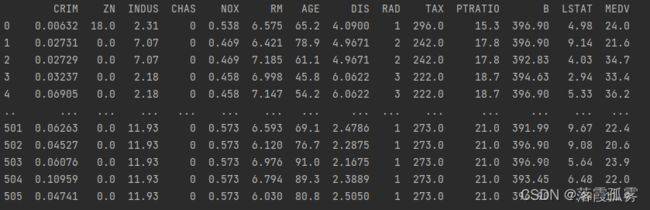
修改后，刚才关于x和y值的选取也需要做相应修改：

    x,y = data[col_names[:-1]], data['MEDV'] 

这句话的意思是x的取值为data中除了最后一列以外所有的列，而y的取值为data中名为’MEDV’的一列。

在我们将训练集喂给模型后，我们会得到训练集的系数，也就是各个属性值的权重，我们加入如下代码：

    t = pd.DataFrame(data=model.coef_, index=list(x.columns), columns=['权重'])
    t['权重绝对值'] = np.abs(t['权重'])
    t.sort_values(by='权重绝对值', ascending=False, inplace=True)
    print(t['权重'])

以上代码的第一行是给我们训练集的系数添加了一个列名“权重”，然后添加了一列“权重绝对值”，之后根据权重绝对值对系数进行一个降序的排序，我的输出结果如下：

从这个结果中可以看到，NOX这个值可能对房价的影响最大，并且与房价呈一个负相关的关系，而AGE这个值可能对房价的影响最小。

4.5 模型优化

之前我们得到了13个属性的一次幂对结果的权重，那么有没有可能这些属性值的二次幂对结果的影响更大呢？这里我们可以对代码稍作修改，添加以下代码：

    for col in col_names[:-1]:
        data[col+'2'] = data[col]**2

    # x,y = data[col_names[:-1]], data['MEDV']
    x = data.drop(labels='MEDV', axis=1)
    y = data['MEDV']

通过for循环，将data中的各项属性值的平方放到data后面，列名称为col_names中各项后面加“2”；第5行代码，将data中除了名称为MEDV以外的列全部加入x，drop后面的axis，为0表示按行删除，1表示按列删除，默认是0；第6行将data中的MEDV列加入y。
运行结果如下：

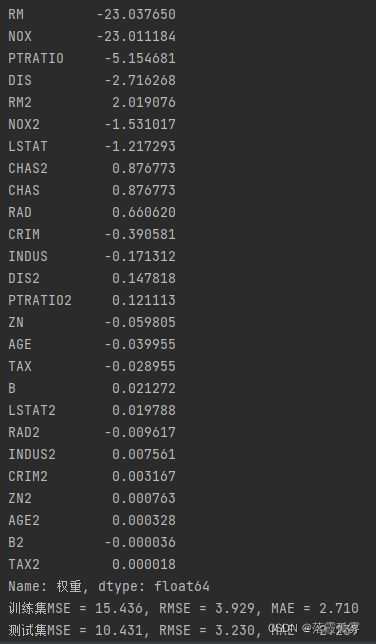
可以看到运行结果要优于4.3中的结果。

在python的sklearn中，可以使用Pipeline实现以上的过程（Pipeline的具体使用方式后面的文章会讲），需要引入以下包：

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

初始化模型时，用以下语句：

    model = Pipeline([
        ('poly', PolynomialFeatures(degree=2)),
        ('LinearRegression', LinearRegression())
    ])

在获取权重和截距时，使用以下语句：

    print("权重：", model.get_params()['LinearRegression'].coef_)
    print("截距：", model.get_params()['LinearRegression'].intercept_)

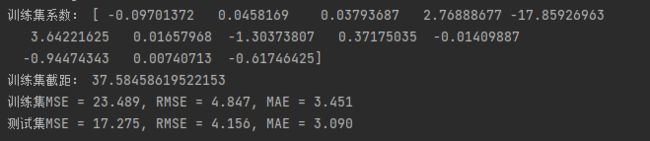
运行结果如下：

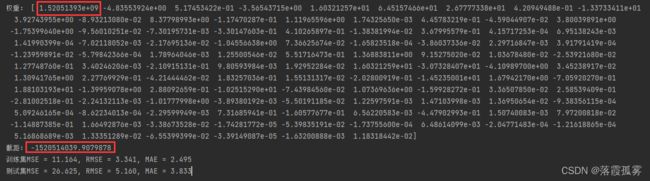
可以看到，截距非常大，权重的第一个值也非常大，这个结果显然是过拟合的。

继续优化，可以使用sklearn中的MinMaxScaler，使用数据归一化的方式优化我们的数据，关于数据归一化的内容具体可以看这篇博文。添加以下包：

from sklearn.preprocessing import PolynomialFeatures, MinMaxScaler

修改模型：

    model = Pipeline([
        ('mms', MinMaxScaler()),
        ('poly', PolynomialFeatures(degree=2)),
        ('LinearRegression', LinearRegression())
    ])

运行结果有的时候会很好，有的时候很差，跟我们的随机选取的训练集有关，较好的结果如下：

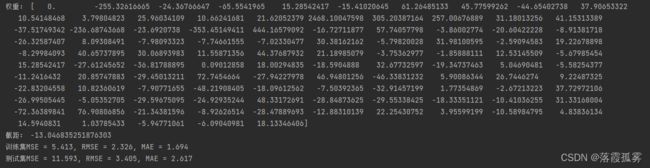
差的结果如下：

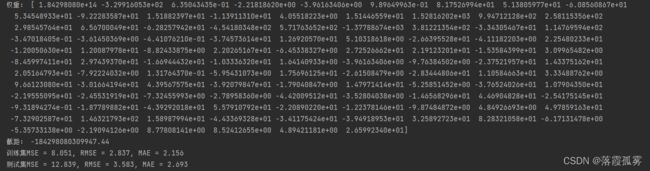
也可以不用LinearRegression，而使用Ridge或者Lasso来回归，加入包：

from sklearn.linear_model import LinearRegression, Ridge, Lasso

初始化模型改为：

    model = Pipeline([
        ('mms', MinMaxScaler()),
        ('poly', PolynomialFeatures(degree=2)),
        # ('LinearRegression', LinearRegression())
        ('ridge', Ridge(alpha=1.0))
    ])

输出改为：

    print("权重：", model.get_params()['ridge'].coef_)
    print("截距：", model.get_params()['ridge'].intercept_)

运行结果如下：

本节最终代码如下：

import math
import numpy as np
import pandas as pd
import sklearn
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, MinMaxScaler

if __name__ == '__main__':
    np.set_printoptions(suppress=True)
    pd.set_option('display.width', 1000)
    pd.set_option('display.max_columns', 30)
    np.set_printoptions(suppress=True, linewidth=150)
    col_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
    data = pd.read_csv('housing.data', sep='\s+', header=None, names = col_names)
    print(data)

    # m, _ = data.shape   # 获取data的行数
    # index = np.arange(m)
    # print(index)
    # np.random.shuffle(index)
    # print(index)
    # test_size = int(m*0.2)
    # test_data = data.loc[index[:test_size], :]
    # print(test_data)
    # train_data = data.loc[index[test_size:], :]
    # print(train_data)

    model = Pipeline([
        ('mms', MinMaxScaler()),
        ('poly', PolynomialFeatures(degree=2)),
        # ('LinearRegression', LinearRegression())
        ('ridge', Ridge(alpha=1.0))
    ])

    # x,y = data.loc[:, :12], data.loc[:, 13] # loc的slice收尾都包括
    # x, y = data[np.arange(13)], data[13]

    # for col in col_names[:-1]:
    #     data[col+'2'] = data[col]**2

    # x,y = data[col_names[:-1]], data['MEDV']
    x = data.drop(labels='MEDV', axis=1)
    y = data['MEDV']
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
    # print(x_test, x_train)

    # model = LinearRegression()  # 调用构造函数
    # print(model)
    model.fit(x_train, y_train)
    # print('训练集系数：', model.coef_)
    # print('训练集截距：', model.intercept_)

    print("权重：", model.get_params()['ridge'].coef_)
    print("截距：", model.get_params()['ridge'].intercept_)
    # t = pd.DataFrame(data=model.coef_, index=list(x.columns), columns=['权重'])
    # t['权重绝对值'] = np.abs(t['权重'])
    # t.sort_values(by='权重绝对值', ascending=False, inplace=True)
    # print(t['权重'])

    y_train_pred = model.predict(x_train)

    # print(np.mean((y - y_pred) ** 2))

    mse_train = mean_squared_error(y_train, y_train_pred)
    rmse_train = math.sqrt(mse_train)
    mae_train = mean_absolute_error(y_train, y_train_pred)
    print('训练集MSE = %.3f, RMSE = %.3f, MAE = %.3f' % (mse_train, rmse_train, mae_train))

    y_test_pred = model.predict(x_test)

    mse_test = mean_squared_error(y_test, y_test_pred)
    rmse_test = math.sqrt(mse_test)
    mae_test = mean_absolute_error(y_test, y_test_pred)

    print('测试集MSE = %.3f, RMSE = %.3f, MAE = %.3f' % (mse_test, rmse_test, mae_test))

同样也可以使用lasso来进行回归。