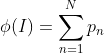David P.Williams论文系列 Muesli_基于声呐图像寻雷难度的图像复杂度度量
摘要
Muesli是一种新的图像复杂度度量手段,它融合了间隙度的概念(像素强度变化的度量)和空间信息的概念(捕捉边缘信息的量)。它能成功地量化在合成孔径声纳(SAS)图像中执行目标探测的相对难度。这已通过一项人类操作员研究的结果和一种目标检测算法的结果进行了实验验证,使用了一组在不同环境中收集的3000多张SAS图像(SAS图像指的是合成孔径声呐图像)。在前一种评价方法中,观察到人类对图像难度的主观排名与复杂度值之间有很好的相关性。在后一种检查方法中,可以观察到检测算法产生假报警的程度和遗漏真实目标的程度都与图像的复杂度值成正比。
关键词:图像复杂度、性能估计、水雷对抗(MCM)、自动目标识别(ATR)、合成孔径声纳(SAS)
介绍
在水雷对抗(MCM)方面,量化图像的复杂性使人们能够预测或估计性能,或适应自动目标识别(A TR)算法的参数。最近在声纳成像的文献中提出了几种不同的复杂性度量,包括基于小波[1]-[3]和间隙度[4]的方法。这项工作的目的是引入和评估一个新的复杂性度量。
本文第二节介绍了新的Muesli图像复杂度度量,第三节详细介绍了评估它的声纳数据。通过操作者实验和检测算法量建立地面真相的方法在第四节中描述。在第六节作结论性评论之前,第五节提出了对新度量的实验评价。
基于小波的方法
[1]O. Daniell, Y . Petillot, and S. Reed, “Unsupervised sea-floor classifica-tion for automatic target recognition,” in Proc. International Conferenceon Underwater Remote Sensing, 2012.
[2]E. Fakiris, D. Williams, M. Couillard, and W. Fox, “Sea-floor acous-tic anisotropy and complexity assessment towards prediction of ATR performance,” in Proc. International Conference and Exhibition on Underwater Acoustics, 2013, pp. 1277–1284.
[3]M. Geilhufe and Ø. Midtgaard, “Quantifying the complexity in sonar images for MCM performance estimation,” in Proc. International Con-ference and Exhibition on Underwater Acoustics, 2014, pp. 1041–1048.
基于间隙度的方法
[4]D. Williams, “Fast unsupervised seafloor characterization in sonar imagery using lacunarity,” IEEE Transactions on Geoscience and Remote Sensing, vol. 53, no. 11, pp. 6022–6034, 2015.
图像复杂性度量
间隙度的方法最初是作为一种测量二值数据空间结构的方法而发展起来的,但这一概念后来被推广到量化灰度图像中的像素强度变化。在我们的公式中,间隙度与闪烁指数,k分布的(逆)形状参数和变异系数等概念密切相关。
灰度图像中一组像素的间隙度是像素值的方差与像素值均值的平方之比。在形式上,我们定义像素![]() (它的索引是在一个基数为
(它的索引是在一个基数为![]() 的集合
的集合![]() 中)的间隙度为:
中)的间隙度为:
基数是集合论中描述任意集合大小的概念。
其中有
并且
当集合N对应于构成矩形像素块的索引时,可以使用积分图像非常快速地完成此计算。对图像中的每个像素重复这个过程,有效地创建了一个间隙度的“地图”,量化局部像素强度变化。
相比之下,空间信息是描述捕获边缘信息的量。设![]() 和
和![]() 分别表示用水平Sobel核和垂直Sobel核对图像
分别表示用水平Sobel核和垂直Sobel核对图像![]() 进行滤波的结果。
进行滤波的结果。
Sobel算子(核)
- 离散微分算子,用来计算图像灰度的近似梯度;
- Sobel算子功能集合高斯平滑和微分求导;
- 又被称为一阶微分算子,求导算子,在水平和垂直两个方向上求导,得到图像X方向和Y方向的梯度图像。
每个像素点的空间信息可以得到为:
然而,在这项工作中,我们没有使用原始声纳图像![]() 作为计算空间信息的输入,而是使用从预定义窗口上的图像
作为计算空间信息的输入,而是使用从预定义窗口上的图像![]() 计算出的间隙图
计算出的间隙图![]() ,该窗口的大小与感兴趣的对象相关(在本论文中,窗口为0.75 m×0.75 m)。这个特定空间信息量的平均值,在所有像素上的平均值,就是我们感兴趣的度量。即新的图像复杂度度量为原始声纳图像的间隙度的空间信息的均值:
,该窗口的大小与感兴趣的对象相关(在本论文中,窗口为0.75 m×0.75 m)。这个特定空间信息量的平均值,在所有像素上的平均值,就是我们感兴趣的度量。即新的图像复杂度度量为原始声纳图像的间隙度的空间信息的均值:![]() 。为了简洁起见,我们创造了“muesli”这个术语来表示这个新的运算符
。为了简洁起见,我们创造了“muesli”这个术语来表示这个新的运算符![]() (这个名字暗指运算符的混合性质和它的字典编纂)。
(这个名字暗指运算符的混合性质和它的字典编纂)。
由于在[4](上文提到的间隙度的方法)中研究了在声纳图像中描述海底的间隙度的效用,我们将提议的muesli复杂度度量与5个密切相关的潜在替代度量进行了比较,包括:
- 原始声纳图像的间隙均值
 ;
; - 原始声纳图像的空白度的变化
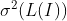 ;
; - 原始声纳图像的间隙度的间隙度
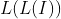 ;
; - 原始声纳图像的间隙度空间信息的变化
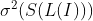 ;
; - 原始声呐图像的间隙度的空间信息的间隙度
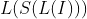 。
。
在每种情况下,与声纳图像场景相关的复杂性度量是一个标量。
因为这块有加了窗,所以对一幅声呐图像来说有均值和方差。
声纳数据集
为了评估所提出的用于确定声纳图像中寻雷难度的图像复杂度指标的价值,我们利用了CMRE的MUSCLE自主水下航行器(AUV)收集的大量数据。这款试验性的、最先进的AUV直径21英寸,来自蓝鳍公司,配备了Thales公司开发的高频SAS系统。SAS的中心频率为300khz,带宽为60khz。该系统能够形成高分辨率声纳图像,理论沿航迹分辨率为2.5厘米,理论跨航迹分辨率为1.25厘米,通常达到150米的范围(示例图像将如下图所示,由于篇幅有限,下图只展示一个)。
![]()
上图显示了各种海洋实验中环境多样性的示例图像;文中还给出了提出的muesli复杂度度量值。
测量的SAS数据是在2008年至2016年期间在地中海、波罗的海和北海的不同地理地点进行的12次海洋实验中收集的。在每个场址,在进行MUSCLE AUV数据收集调查之前,已经部署了各种实际形状的人工地雷目标-圆柱、截锥、楔形。本研究考虑了3723个SAS图像场景,每个场景至少包含一个目标。表一总结了数据集的特点。
ground truth
为了确定哪一种复杂性指标能准确反映搜寻地雷图像的困难程度,必须首先建立一些基本事实的概念。为此目的使用了两种方法:几个不同的人工操作员的评级,以及与自动检测算法性能相关的数量。
人类操作员评级
MCM操作员的主要任务是在声纳图像中识别目标。通过实验获得了作为操作员的人类对数据集中SAS图像复杂性的主观评分。具体来说,每个参与者都被要求对给定的SAS图像的复杂性进行评分——1到5分,5分是最复杂的——根据他或她认为由于环境的原因,在图像中寻找地雷的难度。(参与者没有被要求检测图像中的目标。)呈现给每个人的图像顺序是随机的。
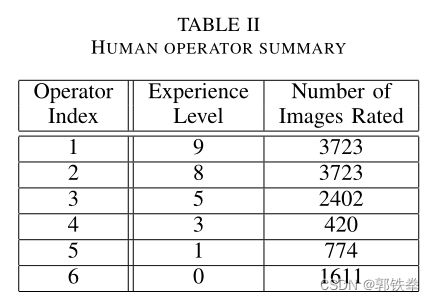
六个人参与了这些操作员实验。每个参与者还被要求自我评估他或她的声纳图像工作经验水平,从0(没有经验)到10。这个自我评估的结果,以及每个人打分的图像数量,如表二所示。可以看出,参与者在经历方面形成了一个多元化的群体。
检测算法得分
除了人工操作员评分,另外两个基于自动检测算法性能的量也被用于更客观地确定图像复杂度。使用的检测算法称为蒙德里安检测器,它基于不同块或区域的平均像素强度执行一系列测试,这些块或区域在图像中共享一个特殊的预定义空间排列该算法应用于数据集中的每张图像。对于给定的图像,算法生成一组告警,每个告警都与分数![]() 相关,可以将其视为告警成为目标的概率。
相关,可以将其视为告警成为目标的概率。
在图像中寻找地雷可能是困难的,原因有两个:一是存在大量杂波物体(即假警报),二是海底条件使发现真正目标具有挑战性。因此,我们通过两个互补的度量来定义在给定图像中进行扫雷的难度,一个与虚警倾向有关,另一个与探测真实目标的能力有关。
具体来说,对于图像![]() ,我们称前者为“虚警分数总和”,并将其定义为:
,我们称前者为“虚警分数总和”,并将其定义为:
![]() 是第
是第![]() 次误报成为目标的概率,即为探测器的“分数”。
次误报成为目标的概率,即为探测器的“分数”。![]() 为探测器在图像中产生的误报次数。这个数量比简单的虚警数量的计数信息量更大,而且它允许更细的复杂性分级(例如,值是连续的而不是离散的)。
为探测器在图像中产生的误报次数。这个数量比简单的虚警数量的计数信息量更大,而且它允许更细的复杂性分级(例如,值是连续的而不是离散的)。
第二个性能量我们称之为“漏报分数总和”,并将其定义为:
其中![]() 是第
是第![]() 个目标成为目标的概率是多少,即为探测器的“分数”。M是图像中真实目标的数量,对于任何未被检测到的目标,
个目标成为目标的概率是多少,即为探测器的“分数”。M是图像中真实目标的数量,对于任何未被检测到的目标,![]() 。可以很容易地看出,这个数量表示目标在多大程度上没有被高概率检测到。例如,当图像中的所有目标未被检测到时,
。可以很容易地看出,这个数量表示目标在多大程度上没有被高概率检测到。例如,当图像中的所有目标未被检测到时,![]() 。当所有的目标都被检测到得分很高时,
。当所有的目标都被检测到得分很高时,![]() 。这个(连续的)数量比一个简单的(离散的)未达到目标的数量或比例的计数更有信息量。
。这个(连续的)数量比一个简单的(离散的)未达到目标的数量或比例的计数更有信息量。
因此,对于一个被认为是高复杂度的图像,人们会期望![]() 和(或)
和(或)![]() 会很大。
会很大。
验证
标准(皮尔逊Pearson)相关函数度量两个变量之间的线性关系的强度。然而,考虑到基本ground truth量的性质,使用斯皮尔曼秩(Spearman rank)相关更有意义,它可以用一个单调函数(不一定是线性函数)衡量两个变量之间的关系。也就是说,我们感兴趣的是确定第二节中列出的复杂度指标——特别是muesli复杂度指标——是否随着人工操作员对复杂度的排序的增加,以及误报评分和错过目标评分和的增加而增加。因此,本文中的“相关”一词总是指斯皮尔曼(Spearman)相关。
首先,我们研究了不同操作员的复杂性评级之间的相关性。这些成对的相关性如表三所示。(只有被两个操作人员评分的图像才被用于计算。)可以看到,评级是相当强的相关性,表明在图像复杂性方面,不同操作员的普遍一致。在表中,每个操作符的最高(非自动)相关性(按行计算)以粗体显示。有趣的是,我们还可以观察到,在经验更丰富的操作员之间,评级的相关性通常更高(参见表二)。
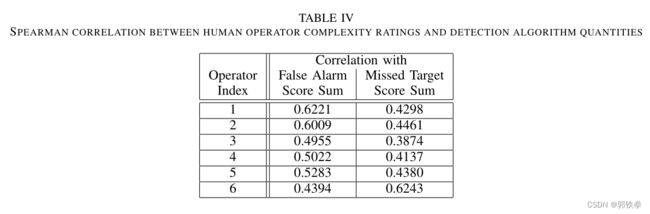
接下来,计算人类操作员的评分与两个检测算法数量之间的相关性,结果如表四所示。可以看出,与虚警评分和![]() 的一致性要强于与漏报目标评分和
的一致性要强于与漏报目标评分和![]() 的一致性。这一结果潜在地表明,人类操作员对图像复杂性的评级更多地受图像中普遍存在的虚警源的影响,而不是受可能掩盖目标检测的因素的影响。未来的研究将更深入地检验这一假设。
的一致性。这一结果潜在地表明,人类操作员对图像复杂性的评级更多地受图像中普遍存在的虚警源的影响,而不是受可能掩盖目标检测的因素的影响。未来的研究将更深入地检验这一假设。
在建立了基本ground truth量的合理性之后,我们现在可以着手评估复杂性度量的准确性。
实验结果
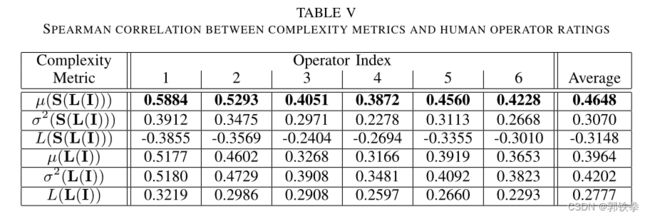
为了评估各种复杂性指标的可行性,计算给定指标与每个操作员评分之间的相关性,结果如表五所示(还显示了每个指标与操作员评分之间的平均相关性,即6个人工操作员的值的平均值)。可以观察到,提出的muesli复杂度度量,即![]() ,为每个操作符(粗体项)实现最大的相关性。
,为每个操作符(粗体项)实现最大的相关性。
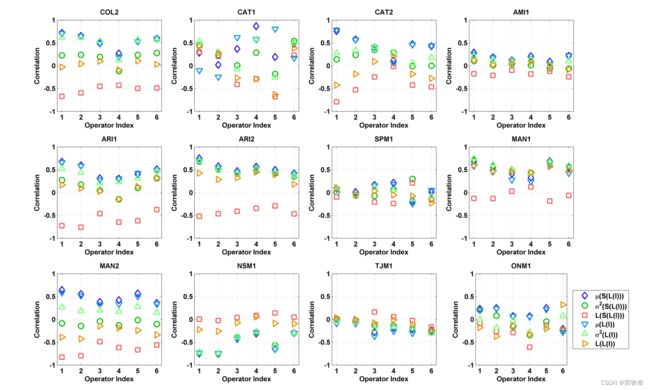
在不同的海洋实验中,环境可能会有明显的不同,因此我们将这些相关性通过实验分解出来,如图2所示。虽然在给定的海洋实验中,不同操作系统的趋势大致相似,但也存在一些差异(例如,在CAT1和SPM1这两个系统中)研究这些海上实验图像的特征,以便更好地理解操作员之间的分歧来源,是很有意义的。
图2 不同复杂度在操作员评级上的相关性
接下来,计算给定度量值与两个检测量之间的相关性,结果如表六所示。可以观察到,提出的muesli复杂度度量值再次与检测量呈强相关性,但![]() 与虚警评分之和的相关性最高。有趣的是,与虚警评分和的相关性始终强于漏报评分和的相关性。
与虚警评分之和的相关性最高。有趣的是,与虚警评分和的相关性始终强于漏报评分和的相关性。
这一结果可能表明,复杂性指标主要是由产生假警报的海底特征的存在所驱动的。
最后,这些相关性作为海洋实验的函数如图3所示。今后研究造成观察到的变化的因素将是有意义的。例如,在NSM1实验中,复杂性指标与检测量没有很强的相关性,由于电流和未补偿的航行器运动,许多图像的质量很差。
结论
提出了一种新的复杂性度量方法,用于确定声纳图像中寻找水雷的难度。研究证明,这种所谓的muesli复杂度度量与人工操作人员对图像复杂度的主观评级密切相关,也与基于自动检测算法的性能度量的更客观的量密切相关。
未来的工作将检查其他复杂性指标的相关性,这些指标来自先前为声纳图像开发的文献。此外,还将进行更多的人工操作实验。