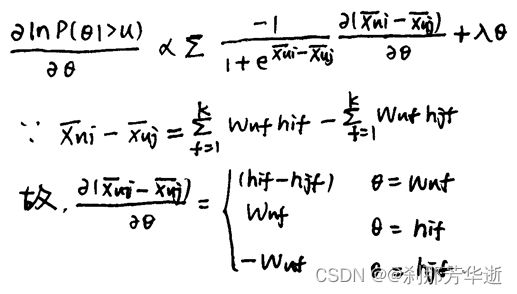BPR算法
目录
什么是BPR算法
BPR算法简介
显示反馈与隐式反馈
矩阵分解的不足
BPR算法
符号定义
BPR算法解决方式
BPR算法两个基本假设
BPR算法推导
贝叶斯定理
BPR推导
BPR算法流程
BPR算法代码与结果
数据
BPR算法代码
BPR结果展示
什么是BPR算法
BPR算法简介
BPR（Bayesian Personalized Ranking），中文名为贝叶斯个性化排序，是推荐系统常用的一种算法。
显示反馈与隐式反馈
- 显示反馈：用户明确表示对物品喜好的行为，如评分、评等级等；
- 隐式反馈：不能明确反映用户喜好的行为，如浏览，点击等；
矩阵分解的不足
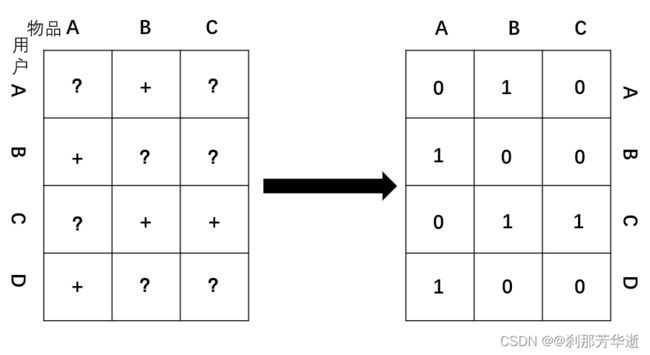
在隐式反馈的情况下，我们使用矩阵分解（MF）时，所收集到的数据均为正样本，而我们标记为零元素的样本分为两种情况：一种是该用户对该物品确实没有兴趣，一种是数据缺失。转换过程如上图所示。对于以上两种情况，我们使用矩阵分解算法时无法进行区别。
而在矩阵分解得到结果之后，常常将预测结果进行排序来为用户进行推荐。BPR算法则是直接排列出推荐物品的相对顺序，并没有预测出具体的评分。
BPR算法
符号定义
用户集U，物品集I，有过隐式反馈记录记作+，无隐式反馈记录记作？。
首先定义偏好关系
，如果用户在物品i和物品j中只对物品i产生了隐式反馈，则说明用户对物品i的喜爱程度大于物品j，则记为
。由以上易知，此关系满足完整性、传递性、反对称性。
BPR算法解决方式
- 对于隐式反馈矩阵进行处理如果一个用户对物品i产生过隐式反馈行为（如：浏览）而对物品j没有产生过行为，则可以构建一个偏好对
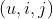，如果一个用户对物品i和物品j都产生过隐式反馈行为，则无法构建偏好对。 - 对每个用户构建其
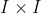的偏好矩阵。
BPR算法两个基本假设
- 每个用户之间的偏好行为相互独立，即用户u在商品i和j之间的偏好和其他用户无关。
- 同一用户对不同物品的偏序相互独立，也就是用户u在商品i和j之间的偏好和其他的商品无关。
BPR算法推导
贝叶斯定理
通常，事件 A 在事件 B 发生的条件下与事件 B 在事件 A 发生的条件下，它们两者的概率并不相同，但是它们两者之间存在一定的相关性，并具有以下公式（称之为“贝叶斯公式”）：
BPR推导
根据贝叶斯公式，有
由于我们假设每一个用户的偏好与其他用户无关，所以对于每一个用户来说，
对该用户的所有物品一样，于是有以下关系：
。所以优化目标可分为两部分，左边的部分与数据集有关，右边部分
与数据集无关。
- 第二部分
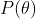
与数据集无关，由于
未知，我们假设其服从均值为0，协方差为
的正态分布，即
。由以上可知，
。
- 第一部分
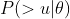
由于我们假设每一个用户喜好的独立性，并且每一个用户对所有物品喜好的独立性，所以有
。
其中，
是sigmoid函数。为什么用sigmoid函数来代替：其实这里的代替可以选择其他的函数，不过式子需要满足BPR的完整性，反对称性和传递性和方便优化计算。
对于
，满足
。
第一部分优化为
。
- 综上，最大化
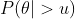就转化成求解下式最大值：
最后，用梯度下降法进行求解，对求导，有：
BPR算法流程
- 随机化初始矩阵W，H；
- 利用梯度下降法进行更新：
- 若W、H收敛，则算法结束，否则进行上一步；
- 计算排序分数
。
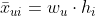BPR算法代码与结果
数据
链接：https://pan.baidu.com/s/1FKYavzmCaTBzeQkQIoThIw
提取码：xbyr
BPR算法代码
- BPR_basic.py
# -*- coding: utf-8 -*-
#引入以下Python库
import random
from collections import defaultdict
import numpy as np
from sklearn.metrics import roc_auc_score
import scores
'''
函数说明:BPR类（包含所需的各种参数）
'''
class BPR:
user_count = 943#用户数
item_count = 1682#项目数
latent_factors = 20#k个主题,k数
lr = 0.01#步长α
reg = 0.01#参数λ
train_count = 10000#训练次数
train_data_path = 'train.txt'#训练集
test_data_path = 'test.txt'#测试集
#U-I的大小
size_u_i = user_count * item_count
# 随机设定的U，V矩阵(即公式中的Wuk和Hik)矩阵
U = np.random.rand(user_count, latent_factors) * 0.01
V = np.random.rand(item_count, latent_factors) * 0.01
biasV = np.random.rand(item_count) * 0.01
#生成一个用户数*项目数大小的全0矩阵
test_data = np.zeros((user_count, item_count))
print("test_data_type",type(test_data))
#生成一个一维的全0矩阵
test = np.zeros(size_u_i)
#再生成一个一维的全0矩阵
predict_ = np.zeros(size_u_i)
#通过文件路径，获取U-I数据
def load_data(self, path):
user_ratings = defaultdict(set)
#输入文件路径path
with open(path, 'r') as f:
for line in f.readlines():
u, i = line.split(" ")
u = int(u)
i = int(i)
user_ratings[u].add(i)
return user_ratings#输出字典user_ratings，为包含U-I的键值对
#输出一个numpy.ndarray文件（n维数组）test_data,其中把含有反馈信息的数据置为1
#通过文件路径，获取测试集数据 获取测试集的评分矩阵
def load_test_data(self, path):
file = open(path, 'r')#测试集文件路径path
for line in file:
line = line.split(' ')
user = int(line[0])
item = int(line[1])
self.test_data[user - 1][item - 1] = 1
#对训练集字典处理，更新分解后两个矩阵
def train(self, user_ratings_train):
for user in range(self.user_count):
# 随机获取一个用户
u = random.randint(1, self.user_count) #找到一个user
# 训练集和测试集不是全都一样的,比如train有948,而test最大为943
if u not in user_ratings_train.keys():
continue
# 从用户的U-I中随机选取1个Item
i = random.sample(user_ratings_train[u], 1)[0] #找到一个item，被评分
# 随机选取一个用户u没有评分的项目
j = random.randint(1, self.item_count)
while j in user_ratings_train[u]:
j = random.randint(1, self.item_count) #找到一个item，没有被评分
#构成一个三元组（uesr,item_have_score,item_no_score)
# python中的取值从0开始
u = u - 1
i = i - 1
j = j - 1
#BPR
r_ui = np.dot(self.U[u], self.V[i].T) + self.biasV[i]
r_uj = np.dot(self.U[u], self.V[j].T) + self.biasV[j]
r_uij = r_ui - r_uj
loss_func = -1.0 / (1 + np.exp(r_uij))
# 更新2个矩阵
self.U[u] += -self.lr * (loss_func * (self.V[i] - self.V[j]) + self.reg * self.U[u])
self.V[i] += -self.lr * (loss_func * self.U[u] + self.reg * self.V[i])
self.V[j] += -self.lr * (loss_func * (-self.U[u]) + self.reg * self.V[j])
# 更新偏置项
self.biasV[i] += -self.lr * (loss_func + self.reg * self.biasV[i])
self.biasV[j] += -self.lr * (-loss_func + self.reg * self.biasV[j])
#得到预测矩阵/评分矩阵predict
def predict(self, user, item):
predict = np.mat(user) * np.mat(item.T)
return predict
#主函数
def main(self):
#获取U-I的{1:{2,5,1,2}....}数据
user_ratings_train = self.load_data(self.train_data_path)
#获取测试集的评分矩阵
self.load_test_data(self.test_data_path)
for u in range(self.user_count):
for item in range(self.item_count):
if int(self.test_data[u][item]) == 1:
self.test[u * self.item_count + item] = 1
else:
self.test[u * self.item_count + item] = 0
#训练
for i in range(self.train_count):
self.train(user_ratings_train) #训练10000次完成
predict_matrix = self.predict(self.U, self.V) #将训练完成的矩阵內积
# 预测
self.predict_ = predict_matrix.getA().reshape(-1) #.getA()将自身矩阵变量转化为ndarray类型的变量
print("predict_new",self.predict_)
self.predict_ = pre_handel(user_ratings_train, self.predict_, self.item_count)
auc_score = roc_auc_score(self.test, self.predict_)
print('AUC:', auc_score)
# Top-K evaluation
scores.topK_scores(self.test, self.predict_, 5, self.user_count, self.item_count)
#对结果进行修正，即用户已经产生交互的用户项目进行剔除，只保留没有产生用户项目的交互的数据
def pre_handel(set, predict, item_count):
#确保推荐不是训练集中的正样本
for u in set.keys():
for j in set[u]:
predict[(u - 1) * item_count + j - 1] = 0
return predict
if __name__ == '__main__':
#调用类的主函数
bpr = BPR()
bpr.main()- scores.py
# -*- coding: utf-8 -*-
#引入heapq、numpy、math库
import heapq
import numpy as np
import math
#计算项目top_K分数
def topK_scores(test, predict, topk, user_count, item_count):
PrecisionSum = np.zeros(topk+1)
RecallSum = np.zeros(topk+1)
F1Sum = np.zeros(topk+1)
NDCGSum = np.zeros(topk+1)
OneCallSum = np.zeros(topk+1)
DCGbest = np.zeros(topk+1)
MRRSum = 0
MAPSum = 0
total_test_data_count = 0
for k in range(1, topk+1):
DCGbest[k] = DCGbest[k - 1]
DCGbest[k] += 1.0 / math.log(k + 1)
for i in range(user_count):
user_test = []
user_predict = []
test_data_size = 0
for j in range(item_count):
if test[i * item_count + j] == 1.0:
test_data_size += 1
user_test.append(test[i * item_count + j])
user_predict.append(predict[i * item_count + j])
if test_data_size == 0:
continue
else:
total_test_data_count += 1
predict_max_num_index_list = map(user_predict.index, heapq.nlargest(topk, user_predict))
predict_max_num_index_list = list(predict_max_num_index_list)
hit_sum = 0
DCG = np.zeros(topk + 1)
DCGbest2 = np.zeros(topk + 1)
for k in range(1, topk + 1):
DCG[k] = DCG[k - 1]
item_id = predict_max_num_index_list[k - 1]
if user_test[item_id] == 1:
hit_sum += 1
DCG[k] += 1 / math.log(k + 1)
# precision, recall, F1, 1-call
prec = float(hit_sum / k)
rec = float(hit_sum / test_data_size)
f1 = 0.0
if prec + rec > 0:
f1 = 2 * prec * rec / (prec + rec)
PrecisionSum[k] += float(prec)
RecallSum[k] += float(rec)
F1Sum[k] += float(f1)
if test_data_size >= k:
DCGbest2[k] = DCGbest[k]
else:
DCGbest2[k] = DCGbest2[k-1]
NDCGSum[k] += DCG[k] / DCGbest2[k]
if hit_sum > 0:
OneCallSum[k] += 1
else:
OneCallSum[k] += 0
# MRR
p = 1
for mrr_iter in predict_max_num_index_list:
if user_test[mrr_iter] == 1:
break
p += 1
MRRSum += 1 / float(p)
# MAP
p = 1
AP = 0.0
hit_before = 0
for mrr_iter in predict_max_num_index_list:
if user_test[mrr_iter] == 1:
AP += 1 / float(p) * (hit_before + 1)
hit_before += 1
p += 1
MAPSum += AP / test_data_size
print('MAP:', MAPSum / total_test_data_count)
print('MRR:', MRRSum / total_test_data_count)
print('Prec@5:', PrecisionSum[4] / total_test_data_count)
print('Rec@5:', RecallSum[4] / total_test_data_count)
print('F1@5:', F1Sum[4] / total_test_data_count)
print('NDCG@5:', NDCGSum[4] / total_test_data_count)
print('1-call@5:', OneCallSum[4] / total_test_data_count)
returnBPR结果展示
