CV-SIFT特征匹配算法详解及实现
Python实现SIFT特征匹配算法
- 一. SIFT原理
-
- 1.特征点提取
-
- 1.1 尺度空间
- 1.2 多分辨率图像金字塔
- 1.3 DOG局部极值检测
- 2. 特征点主方向确定
- 3. 特征点描述
-
- 3.1 确定描述子计算区域和并校正主方向
- 3.2 生成描述子
- 二.代码实现
-
- 特征点提取
- 匹配描述子
- 匹配地理标记
一. SIFT原理
尺度不变特征转换(Scale-invariant feature transform或SIFT)是用于图像处理领域的一种描述。这种描述具有尺度不变性,它对物体的尺度变化,刚体变换,光照强度和遮挡都具有较好的稳定性,可在图像中检测出关键点,是一种局部特征描述子。
SIFT算法由 David Lowe在1999年所发表,2004年完善总结。 其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。
局部影像特征的描述与侦测可以帮助辨识物体,SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性,它们是高度显著而且相对容易撷取,在母数庞大的特征数据库中,很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高,甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下,辨识速度可接近即时运算。SIFT特征的信息量大,适合在海量数据库中快速准确匹配。
SIFT 算法被认为是图像匹配效果好的方法之 一算法实现特征匹配主要有三个流程:
①特征点提取;
②特征点主方向确定;
③特征点描述;
④特征点匹配;
其中特征点提取主要包括生成高斯差分(DifferenceofGaussian,DOG)尺度空间、寻找局部极值点、特征点筛选、确定特征点方向;特征点匹配主要包括根据描述子相似性进行匹配、匹配对比值提纯、RANSAC方法剔除离群匹配对。
1.特征点提取
两种图像在匹配的时候可能因为拍摄的距离、拍摄的角度问题,会导致在特征点提取的时候差异很大,所以我们希望SIFT的特征点可以具有尺度不变性和方向不变性。 对于我们人类来说,在一定的范围内,无论物体远还是近,我们都可以一眼分辨出来,当一个人从远处走来的时候,我们可以从轮廓就判断出这是一个人,但是还看不清细节,当他走进的时候,我们才会去注意其他的细节特征。而计算机没有主观意识去识别哪里是特征点,它能做的,只是分辨出变化率最快的点。彩色图是三通道的,不好检测突变点。需要将RGB图转换为灰度图,此时灰度图为单通道,灰度值在0~255之间分布。而且当图像放大或者缩小时,它读取的特征点与原先可能差异很大,所以其中一个办法就是把物体的尺度空间图像集合提供给计算机,让它针对考虑不同尺度下都存在的特征点。
1.1 尺度空间
尺度空间的基本思想为:高斯核是唯一可以产生多尺度空间的核,在输入的图像模型中,通过高斯模糊函数连续的对尺度进行参数变换,最终得到多尺度空间序列。图像中某一尺度的空间函数 L(x ,y, σ)由可变参数的高斯函数 G(x, y, σ)和原输入图像I(x ,y)卷积得出:
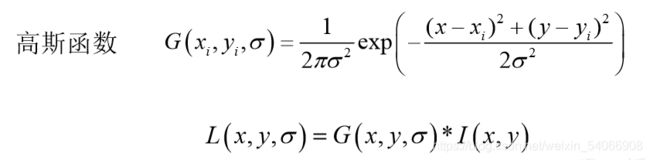
其中,σ 表示为尺度空间因子,σ 越小,反应的局部点越清晰。反之 σ 越大,图像越模糊,越不能反应出图像的细节。
1.2 多分辨率图像金字塔
在早期图像的多尺度通常使用图像金字塔表述形式。图像金字塔是同一图象在不同的分辨率下得到的一组结果,其生成过程一半包含两个步骤:
(1)对图像做高斯平滑(高斯模糊)。
(2)对图像做降采样,降维采样后得到一系列尺寸不断缩小的图像。
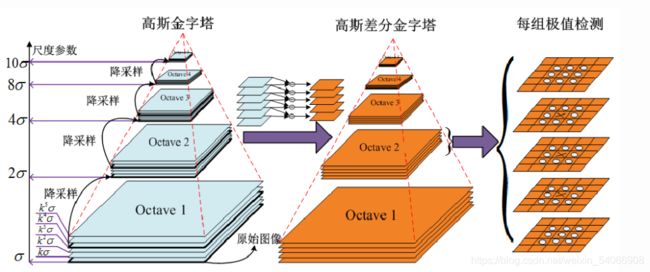
传统的SIFT算法是通过建立高斯差分函数(DOG) 方法来提取特征点。首先,在不同尺度参数的组数中,高斯差分图像是由某一相同尺度层的相邻图像作差值 得出。然后,将得到的差分图像与原图像 I(x, y)做卷积得到公式(3)的 DOG 函数:
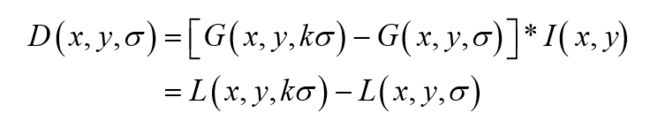
从上式可以知道,将相邻的两个高斯空间的图像相减就得到了DoG的响应图像。为了得到DoG图像,先要构造高斯尺度空间,而高斯的尺度空间可以在图像金字塔降维采样的基础上加上高斯滤波得到,也就是对图像金字塔的每层图像使用不同的尺度参数σ进行高斯模糊,使每层金字塔有多张高斯模糊过的图像,然后我们把得到的同一尺寸大小的图像划分为一组。
1.3 DOG局部极值检测
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点, 每一个像素点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。

中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个 点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。
有些极值点的位置是在图像的边缘位置的,因为图像的边缘点很难定位,同时也容易受到噪声的干扰,我们把这些点看做是不稳定的极值点,需要进行去除。边缘梯度的方向上主曲率值比较大,而沿着边缘方向则主曲率值较小。候选特征点的DoG函数D(x)的主曲率与2×2Hessian矩阵H的特征值成正比,Dxx表示DOG金字塔中某一尺度的图像x方向求导两次:
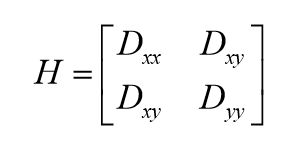
在在边缘梯度的方向上主曲率值比较大,而沿着边缘方向则主曲率值较小。设α=λmax=Dxx为H的最大特征值,β=λmin=Dyy为H的最小特征值,则有:
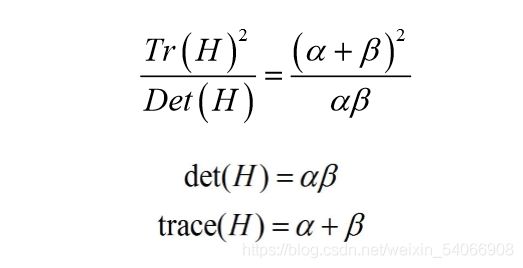
Tr(H) 为矩阵H的迹,Det(H)为矩阵H的行列式.当两个特征值相等时其值最小,因此为了检测主曲率是否在某个阈值Tr下,只需检测该比值与阈值T的大小关系,过滤不稳定的边缘响应点。
所以,特征点提取可以概括为以下几个步骤:
1.构建高斯尺度空间,产生不同尺度的高斯模糊图像。
2.进行降采用,得到一系列尺寸不断缩小的图像。
3.DOG空间极值检测,去除部分边缘响应点。
2. 特征点主方向确定
经过上面的步骤已经找到了在不同尺度下都存在的特征点,为了实现图像旋转不变性,需要给特征点的方向进行赋值。利用特征点邻域像素的梯度来确定其方向参数,再利用图像的梯度直方图求取关键点局部结构的稳定方向。
对于已经检测到的特征点,我们可以得到该特征点的尺度值σ ,所以确定该参数可以得到该尺度下的高斯图像:
![]()
我们通过每个极值点的梯度来为极值点赋予方向,梯度幅值等于上下两点像素值差的平方加上左右两点像素值差的平方,梯度方向则为上下两点像素值差与左右两点像素值差的商。
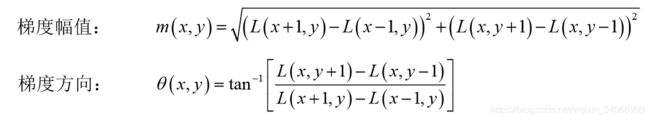
当然,我们的目标是用特征点邻域像素的梯度来确定其方向参数,确定关键点的方向采用梯度直方图统计法,统计以关键点为原点,一定区域内的图像像素点对关键点方向生成所作的贡献。

通过以上的图可以看出,梯度方向角为横轴刻度,取45度为一个单位,那么横轴就有8个刻度;纵轴是对应梯度的幅值累加值。
关键点主方向:极值点周围区域梯度直方图的主峰值也是特征点方向。
关键点辅方向:在梯度方向直方图中,当存在另一个相当于主峰值 80%能量的峰值时,则将这个方向认为是该关键点的辅方向。
图中所示的是180度方向为主方向,45度方向可以看做是辅方向。仅有15%的关键点被赋予多个方向,但可以明显的提高关键点匹配的稳定性 。
3. 特征点描述
通过以上步骤,对于每一个关键点,拥有三个信息:位置、尺度以及方向。接下来就是为每个关键点建立一个描述符,使其不随各种变化而改变,比如光照变化、视角变化等等。并且描述符应该有较高的独特性,以便于提高特征点正确匹配的概率。
3.1 确定描述子计算区域和并校正主方向
在计算描述子之前,我们需要先确定计算区域,Lowe实验结果表明: 描述子采用4×4×8=128维向量表征,综合效果最优 (不变性与独特性)。
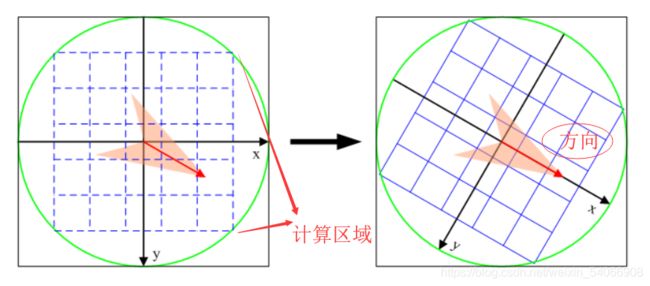
为了保证特征矢量具有旋转不变性,需要以特征点为中心,将特征点附近邻域内图像梯度的位置和方向旋转一个方向角θ,即将原图像x轴转到与主方向相同的方向。
3.2 生成描述子
下图所示,左图的中央为当前关键点的位置,每个小格代表为关键点邻域所在尺度空间的一个像素,求取每个像素的梯度幅值与梯度方向,箭头方向代表该像素的梯度方向,长度代表梯度幅值,然后利用高斯窗口对其进行加权运算。最后在每个3σ×3σ的小块上(图像中每个正方形的区域的边长为4)绘制8个方向的梯度直方图,计算每个梯度方向的累加值,即可形成一个种子点,如右图所示。每个特征点由4个种子点组成,每个种子点有8个方向的向量信息。这种邻域方向性信息联合增强了算法的抗噪声能力,同时对于含有定位误差的特征匹配也提供了比较理性的容错性。

在实际的计算过程中,为了增强匹配的稳健性,Lowe建议对每个关键点使用4×4共16个种子点来描述,这样一个关键点就可以产生128维的SIFT特征向量。

这个128维的SIFT特征向量就像是我们每个人的身份证一样,拥有绝对标识,几乎不可能重复,在这里可以对128维向量进行归一化处理,可以去除光照变化的影响。我们对模板图和目标图分别建立描述子集合。特征点的匹配是通过两点集合内关键点描述子的比对来完成,描述子的相似度量采用欧氏距离。假设如下:
二.代码实现
特征点提取
features.py
from numpy import loadtxt, array, concatenate, zeros, dot, arccos
from numpy.linalg import linalg
from pylab import *
from PIL import Image
from numpy import *
import os
from numpy import loadtxt, arange, cos, sin, pi
def process_image(imagename, resultname, params="--edge-thresh 10 --peak-thresh 5"):
"""处理一幅图像,然后将结果保存在文件中"""
if imagename[-3:] != 'pgm':
# 创建一个pgm文件
im = Image.open(imagename).convert('L')
im.save('tmp.pgm')
imagename = 'tmp.pgm'
cmmd = str("C:/Users/Administrator/Desktoplfeat-0.9.20-binlfeat-0.9.20/bin/win64/sift.exe " + imagename + " --output=" + resultname + " " + params)
os.system(cmmd)
print('processed', imagename, 'to', resultname)
def read_features_from_file(filename):
"""读取特征值属性值,然后将其以矩阵形式返回"""
f = loadtxt(filename)
return f[:, :4], f[:, 4:] # 特征位置,描述子
def plot_features(im, locs, circle=False):
"""显示带有特征的图像
输入:im(数组图像),locs(每个特征的行、列、尺度和方向角度)"""
def draw_circle(c,r):
t = arange(0,1.01,.01)*2*pi
x = r*cos(t) + c[0]
y = r*sin(t) + c[1]
plot(x,y,'b',linewidth=2)
imshow(im)
if circle:
for p in locs:
draw_circle(p[:2],p[2])
else:
plot(locs[:,0],locs[:,1],'ob')
axis('off')
return
def match(desc1, desc2):
"""对于第一幅图像的每个描述子,选取其在第二幅图像中的匹配
输入:desc1(第一幅图像中的描述子),desc2(第二幅图像中的描述子)"""
desc1 = array([dnalg.norm(d) for d in desc1])
desc2 = array([dnalg.norm(d) for d in desc2])
dist_ratio = 0.6
desc1_size = desc1.shape
matchscores = zeros((desc1_size[0],1), 'int')
desc2t = desc2.T #预先计算矩阵转置
for i in range(desc1_size[0]):
dotprods = dot(desc1[i,:], desc2t) #向量点乘
dotprods = 0.9999*dotprods
# 反余弦和反排序,返回第二幅图像中特征的索引
index = argsort(arccos(dotprods))
# 检查最近邻的角度是否小于dist_ratio乘以第二近邻的角度
if arccos(dotprods)[index[0]] < dist_ratio * arccos(dotprods)[index[1]]:
matchscores[i] = int(index[0])
return matchscores
def match_twosided(desc1,decs2):
"""双向对称版本的match"""
matches_12 = match(desc1, decs2)
matches_21 = match(decs2, decs2)
ndx_12 = matches_12.nonzero()[0]
# 去除不对称匹配
for n in ndx_12:
if matches_21[int(matches_12[n])] != n:
matches_12[n] = 0
return matches_12
def appendimages(im1, im2):
"""返回将两幅图像并排拼接成的一幅新图像"""
# 选取具有最少行数的图像,然后填充足够的空行
row1 = im1.shape[0]
row2 = im2.shape[0]
if row1 < row2:
im1 = concatenate((im1,zeros((row2-row1,im1.shape[1]))), axis=0)
elif row1 > row2:
im2 = concatenate((im2,zeros((row1-row2,im2.shape[1]))), axis=0)
# 如果这些情况都没有,那么他们的行数相同,不需要进行填充
return concatenate((im1,im2), axis=1)
if __name__ == '__main__':
imname = '10.jpg'
im1 = array(Image.open(imname).convert('L'))
process_image(imname, '10.sift')
l1, d1 = read_features_from_file('file_sift/10.sift')
figure()
gray()
plot_features(im1, l1, circle=True)
show()
运行结果:
原图:
匹配描述子
sift.py
from numpy import loadtxt, array, concatenate, zeros, dot, arccos
from numpy.core import vstack
from numpy.linalg import linalg
from pylab import *
from PIL import Image
from nnumpy import *
import os
from numpy import loadtxt, arange, cos, sin, pi
def process_image(imagename, resultname, params="--edge-thresh 10
--peak-thresh 5"):
"""处理一幅图像,然后将结果保存在文件中"""
if imagename[-3:] != 'pgm':
# 创建一个pgm文件
im = Image.open(imagename).convert('L')
im.save('tmp.pgm')
imagename = 'tmp.pgm'
cmmd = str("C:/Users/Administrator/Desktop/vlfeat-0.9.20-bin/vlfeat-0.9.20/bin/win64/sift.exe
" + imagename + " --output=" + resultname + " " +
params)
os.system(cmmd)
print('processed', imagename, 'to',
resultname)
def read_features_from_file(filename):
"""读取特征值属性值,然后将其以矩阵形式返回"""
f = loadtxt(filename)
return f[:, :4], f[:, 4:] # 特征位置,描述子
def
plot_features(im, locs, circle=False):
"""显示带有特征的图像
输入:im(数组图像),locs(每个特征的行、列、尺度和方向角度)"""
def draw_circle(c,r):
t = arange(0,1.01,.01)*2*pi
x = r*cos(t) + c[0]
y = r*sin(t) + c[1]
plot(x,y,'b',linewidth=2)
imshow(im)
if circle:
for p in locs:
draw_circle(p[:2],p[2])
else:
plot(locs[:,0],locs[:,1],'ob')
axis('off')
return
def match(desc1, desc2):
"""对于第一幅图像的每个描述子,选取其在第二幅图像中的匹配
输入:desc1(第一幅图像中的描述子),desc2(第二幅图像中的描述子)"""
desc1 = array([d/linalg.norm(d) for d in
desc1])
desc2 = array([d/linalg.norm(d) for d in
desc2])
dist_ratio = 0.6
desc1_size = desc1.shape
matchscores = zeros((desc1_size[0],1),
'int')
desc2t = desc2.T #预先计算矩阵转置
for i in range(desc1_size[0]):
dotprods = dot(desc1[i,:], desc2t) #向量点乘
dotprods = 0.9999*dotprods
# 反余弦和反排序,返回第二幅图像中特征的索引
index = argsort(arccos(dotprods))
# 检查最近邻的角度是否小于dist_ratio乘以第二近邻的角度
if arccos(dotprods)[index[0]] <
dist_ratio * arccos(dotprods)[index[1]]:
matchscores[i] = int(index[0])
return matchscores
def match_twosided(desc1,decs2):
"""双向对称版本的match"""
matches_12 = match(desc1, decs2)
matches_21 = match(decs2, decs2)
ndx_12 = matches_12.nonzero()[0]
# 去除不对称匹配
for n in ndx_12:
if matches_21[int(matches_12[n])] != n:
matches_12[n] = 0
return matches_12
def appendimages(im1, im2):
"""返回将两幅图像并排拼接成的一幅新图像"""
# 选取具有最少行数的图像,然后填充足够的空行
row1 = im1.shape[0]
row2 = im2.shape[0]
if row1 < row2:
im1 =
concatenate((im1,zeros((row2-row1,im1.shape[1]))), axis=0)
elif row1 > row2:
im2 =
concatenate((im2,zeros((row1-row2,im2.shape[1]))), axis=0)
# 如果这些情况都没有,那么他们的行数相同,不需要进行填充
return concatenate((im1,im2), axis=1)
def plot_matches(im1, im2, locs1, locs2, matchscores, show_below=True):
"""显示一幅带有连接匹配之间连线的图片
输入:im1,im2(数组图像),locs1,locs2(特征位置),matchscores(match的输出),
show_below(如果图像应该显示再匹配下方)"""
im3 = appendimages(im1,im2)
if show_below:
im3 = vstack((im3,im3))
imshow(im3)
cols1 = im1.shape[1]
for i in range(len(matchscores)):
if matchscores[i] > 0:
plot([locs1[i, 0],
locs2[matchscores[i, 0], 0] + cols1], [locs1[i, 1], locs2[matchscores[i, 0],
1]], 'c')
axis('off')
if
__name__ == '__main__':
# imname = 'raccoon.jpg'
# im1 = array(Image.open(imname).convert('L'))
# process_image(imname, 'raccoon.sift')
# l1, d1 =
read_features_from_file('raccoon.sift')
im1f = r'12.jpg'
im2f = r'13.jpg'
im1 = array(Image.open(im1f))
im2 = array(Image.open(im2f))
process_image(im1f, 'out_sift_1.txt')
l1, d1 =
read_features_from_file('out_sift_1.txt')
figure()
gray()
subplot(121)
plot_features(im1, l1, circle=False)
process_image(im2f, 'out_sift_2.txt')
l2, d2 =
read_features_from_file('out_sift_2.txt')
subplot(122)
plot_features(im2, l2, circle=False)
matches = match_twosided(d1, d2)
print('{} matches'.format(len(matches.nonzero()[0])))
figure()
gray()
plot_matches(im1, im2, l1, l2, matches,
show_below=True)
show()
match.py
from PIL import Image
from numpy import array
from pylab import *
import sys
from VC.SIFT import sift
if len(sys.argv) >= 3:
im1f, im2f = sys.argv[1], sys.argv[2]
else:
# im1f = '../data/sf_view1.jpg'
# im2f = '../data/sf_view2.jpg'
im1f = '12.jpg'
im2f = '13.jpg'
#
im1f = '../data/climbing_1_small.jpg'
#
im2f = '../data/climbing_2_small.jpg'
im1 = array(Image.open(im1f))
im2 = array(Image.open(im2f))
sift.process_image(im1f, 'out_sift_1.txt')
l1, d1 =
sift.read_features_from_file('out_sift_1.txt')
figure()
gray()
subplot(121)
sift.plot_features(im1, l1, circle=False)
sift.process_image(im2f, 'out_sift_2.txt')
l2, d2 =
sift.read_features_from_file('out_sift_2.txt')
subplot(122)
sift.plot_features(im2, l2, circle=False)
# matches = sift.match(d1, d2)
matches = sift.match_twosided(d1, d2)
print('{}
matches'.format(len(matches.nonzero()[0])))
figure()
gray()
sift.plot_matches(im1, im2, l1, l2,
matches, show_below=True)
show()
运行结果:
同一张图:3079 matches
所摄为集美大学竞武馆
匹配地理标记
lines.py
记得压缩图片,否则运行时间非常慢
import os
import imtools
from numpy import zeros
from pylab import *
from PIL import Image
import pydot
from VC.SIFT import sift
""" This is the example
graph illustration of matching images from Figure 2-10.
To download the images, see
ch2_download_panoramio.py."""
def get_imlist(path):
#
返回目录中所有JPG图像的文件名列表
return [os.path.join(path,f) for f in os.listdir(path) if
f.endswith('.jpg')]
filelist=get_imlist(path)
for infile in filelist:
outfile =
os.path.splitext(infile)[0]+".png"
if infile != outfile:
try:
Image.open(infile).save(outfile)
except IOError:
print("cannot
convert", infile)
download_path =
r"C:\Users\Administrator\Desktop\JMU-pic" # set this to the path where you downloaded
the panoramio images
path = r"C:\Users\Administrator\Desktop" # path to save thumbnails (pydot needs the
full system path)
# list of downloaded filenames
imlist = get_imlist(download_path)
nbr_images = len(imlist)
# extract features
featlist = [imname[:-3] + 'sift' for imname
in imlist]
for i, imname in enumerate(imlist):
sift.process_image(imname, featlist[i])
matchscores = zeros((nbr_images,
nbr_images))
for i in range(nbr_images):
for j in range(i, nbr_images): #
only compute upper triangle
print ('comparing ', imlist[i], imlist[j])
l1, d1 = sift.read_features_from_file(featlist[i])
l2, d2 = sift.read_features_from_file(featlist[j])
matches = sift.match_twosided(d1, d2)
nbr_matches = sum(matches > 0)
print ('number of matches = ', nbr_matches)
matchscores[i, j] = nbr_matches
print ("The match scores is: \n",
matchscores)
# copy values
for i in range(nbr_images):
for j in range(i + 1, nbr_images):
# no need to copy diagonal
matchscores[j, i] = matchscores[i, j]
#可视化
threshold = 2 # min number of matches needed to create link
g = pydot.Dot(graph_type='graph') # don't want the default directed graph
for i in range(nbr_images):
for j in range(i + 1, nbr_images):
if matchscores[i, j] > threshold:
# first image in pair
im = Image.open(imlist[i])
im.thumbnail((100, 100))
filename = path + str(i) + '.png'
im.save(filename) # need
temporary files of the right size
g.add_node(pydot.Node(str(i), fontcolor='transparent',
shape='rectangle', image=filename))
# second image in pair
im = Image.open(imlist[j])
im.thumbnail((100, 100))
filename = path + str(j) + '.png'
im.save(filename) # need
temporary files of the right size
g.add_node(pydot.Node(str(j), fontcolor='transparent',
shape='rectangle', image=filename))
g.add_edge(pydot.Edge(str(i), str(j)))
g.write_png('jmu.png')
# figure()
# imshow(g)
运行结果:
The match scores is:
[[22. 3. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 19. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 13. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 8. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 15. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 18. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 3. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 17. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 10.]]
由于安装问题或是版本问题(没改出来)导致每次运行时都会提示dot.exe停止运行,只有强制关闭的选项,无法看见结果的连线图。但是能看见构造出的连接矩阵。







