【深度学习实战】一、Numpy手撸神经网络实现线性回归
目录
一、引言
二、代码实战
1、Tensor和初始化类
2、全连接层
3、模型组网
4、SGD优化器
5、均方差损失函数
6、Dataset
三、线性回归实战
四、实验结果
五、总结
一、引言
深度学习理论相对简单,但是深度学习框架(tensorflow/torch/paddlepaddle)源码却比较复杂,对于初学者来说,将代码和理论相结合理解是一个巨大的问题,本文的目标是使用python的numpy库从零开始实现一个简单的神经网络模型,并解决一个简单的线性回归问题。本文不会过多介绍理论,直接从代码入手,如需要了解相关理论请参考下方链接。
相关资料参考:
1、全连接层前向传播和梯度计算
2、动量梯度下降
3、ReLU
二、代码实战
1、Tensor和初始化类
Tensor:包含数据和梯度信息,神经网络层的参数已Tensor保存。
初始化类(Constant/Normal):参数初始化方法。
# 因为层的参数需要保存值和对应的梯度,这里定义梯度,可训练的参数全部以Tensor的类别保存
import numpy as np
np.random.seed(10001)
class Tensor:
def __init__(self, shape):
self.data = np.zeros(shape=shape, dtype=np.float32) # 存放数据
self.grad = np.zeros(shape=shape, dtype=np.float32) # 存放梯度
def clear_grad(self):
self.grad = np.zeros_like(self.grad)
def __str__(self):
return "Tensor shape: {}, data: {}".format(self.data.shape, self.data)
# Tensor的初始化类,目前仅提供Normal初始化和Constant初始化
class Initializer:
"""
基类
"""
def __init__(self, shape=None, name='initializer'):
self.shape = shape
self.name = name
def __call__(self, *args, **kwargs):
raise NotImplementedError
def __str__(self):
return self.name
class Constant(Initializer):
def __init__(self, value=0., name='constant initializer', *args, **kwargs):
super().__init__(name=name, *args, **kwargs)
self.value = value
def __call__(self, shape=None, *args, **kwargs):
if shape:
self.shape = shape
assert shape is not None, "the shape of initializer must not be None."
return self.value + np.zeros(shape=self.shape)
class Normal(Initializer):
def __init__(self, mean=0., std=0.01, name='normal initializer', *args, **kwargs):
super().__init__(name=name, *args, **kwargs)
self.mean = mean
self.std = std
def __call__(self, shape=None, *args, **kwargs):
if shape:
self.shape = shape
assert shape is not None, "the shape of initializer must not be None."
return np.random.normal(self.mean, self.std, size=self.shape)2、全连接层
Layer:层的基类,主要包括前向传播和反向传播。
Linear:全连接层,继承自Layer,具体化前向传播和反向传播的参数计算过程。
# 为了使层能够组建起来,实现前向传播和反向传播,首先定义层的基类Layer
# Layer的几个主要方法说明:
# forward: 实现前向传播
# backward: 实现反向传播
# parameters: 返回该层的参数,传入优化器进行优化
class Layer:
def __init__(self, name='layer', *args, **kwargs):
self.name = name
def forward(self, *args, **kwargs):
raise NotImplementedError
def backward(self):
raise NotImplementedError
def parameters(self):
return []
def __call__(self, *args, **kwargs):
return self.forward(*args, **kwargs)
def __str__(self):
return self.name
class Linear(Layer):
"""
input X, shape: [N, C]
output Y, shape: [N, O]
weight W, shape: [C, O]
bias b, shape: [1, O]
grad dY, shape: [N, O]
forward formula:
Y = X @ W + b # @表示矩阵乘法
backward formula:
dW = X.T @ dY
db = sum(dY, axis=0)
dX = dY @ W.T
"""
def __init__(
self,
in_features,
out_features,
name='linear',
weight_attr=Normal(),
bias_attr=Constant(),
*args,
**kwargs
):
super().__init__(name=name, *args, **kwargs)
self.weights = Tensor((in_features, out_features))
self.weights.data = weight_attr(self.weights.data.shape)
self.bias = Tensor((1, out_features))
self.bias.data = bias_attr(self.bias.data.shape)
self.input = None
def forward(self, x):
self.input = x
output = np.dot(x, self.weights.data) + self.bias.data
return output
def backward(self, gradient):
self.weights.grad += np.dot(self.input.T, gradient) # dy / dw
self.bias.grad += np.sum(gradient, axis=0, keepdims=True) # dy / db
input_grad = np.dot(gradient, self.weights.data.T) # dy / dx
return input_grad
def parameters(self):
return [self.weights, self.bias]
def __str__(self):
string = "linear layer, weight shape: {}, bias shape: {}".format(self.weights.data.shape, self.bias.data.shape)
return string
class ReLU(Layer):
"""
forward formula:
relu = x if x >= 0
= 0 if x < 0
backwawrd formula:
grad = gradient * (x > 0)
"""
def __init__(self, name='relu', *args, **kwargs):
super().__init__(name=name, *args, **kwargs)
self.activated = None
def forward(self, x):
x[x < 0] = 0
self.activated = x
return self.activated
def backward(self, gradient):
return gradient * (self.activated > 0) 3、模型组网
Sequential:模型组网类,将神经网络的层按照顺序叠加起来,实现顺序前向传播和反向传播。
# 模型组网的功能是将层串起来,实现数据的前向传播和梯度的反向传播
# 添加层的时候,按照顺序添加层的参数
# Sequential方法说明:
# add: 向组网中添加层
# forward: 按照组网构建的层顺序,依次前向传播
# backward: 接收损失函数的梯度,按照层的逆序反向传播
class Sequential:
def __init__(self, *args, **kwargs):
self.graphs = []
self._parameters = []
for arg_layer in args:
if isinstance(arg_layer, Layer):
self.graphs.append(arg_layer)
self._parameters += arg_layer.parameters()
def add(self, layer):
assert isinstance(layer, Layer), "The type of added layer must be Layer, but got {}.".format(type(layer))
self.graphs.append(layer)
self._parameters += layer.parameters()
def forward(self, x):
for graph in self.graphs:
x = graph(x)
return x
def backward(self, grad):
# grad backward in inverse order of graph
for graph in self.graphs[::-1]:
grad = graph.backward(grad)
def __call__(self, *args, **kwargs):
return self.forward(*args, **kwargs)
def __str__(self):
string = 'Sequential:\n'
for graph in self.graphs:
string += graph.__str__() + '\n'
return string
def parameters(self):
return self._parameters4、SGD优化器
Optimizer:优化器基类,包括参数优化方法(step)、清空梯度(clear_grad)、计算正则化(get_decay)。
SGD:随机梯度下降类,实现了动量梯度下降方法。
# 优化器主要完成根据梯度来优化参数的任务,其主要参数有学习率和正则化类型和正则化系数
# Optimizer主要方法:
# step: 梯度反向传播后调用,该方法根据计算出的梯度,对参数进行优化
# clear_grad: 模型调用backward后,梯度会进行累加,如果已经调用step优化过参数,需要将使用过的梯度清空
# get_decay: 根据不同的正则化方法,计算出正则化惩罚值
class Optimizer:
"""
optimizer base class.
Args:
parameters (Tensor): parameters to be optimized.
learning_rate (float): learning rate. Default: 0.001.
weight_decay (float): The decay weight of parameters. Defaylt: 0.0.
decay_type (str): The type of regularizer. Default: l2.
"""
def __init__(self, parameters, learning_rate=0.001, weight_decay=0.0, decay_type='l2'):
assert decay_type in ['l1', 'l2'], "only support decay_type 'l1' and 'l2', but got {}.".format(decay_type)
self.parameters = parameters
self.learning_rate = learning_rate
self.weight_decay = weight_decay
self.decay_type = decay_type
def step(self):
raise NotImplementedError
def clear_grad(self):
for p in self.parameters:
p.clear_grad()
def get_decay(self, g):
if self.decay_type == 'l1':
return self.weight_decay
elif self.decay_type == 'l2':
return self.weight_decay * g
# 基本的梯度下降法为(不带正则化):
# W = W - learn_rate * dW
# 带动量的梯度计算方法(减弱的梯度的随机性):
# dW = (momentum * v) + (1 - momentum) * dW
class SGD(Optimizer):
def __init__(self, momentum=0.9, *args, **kwargs):
super().__init__(*args, **kwargs)
self.momentum = momentum
self.velocity = []
for p in self.parameters:
self.velocity.append(np.zeros_like(p.grad))
def step(self):
for p, v in zip(self.parameters, self.velocity):
decay = self.get_decay(p.grad)
v = self.momentum * v + p.grad + decay # 动量计算
p.data = p.data - self.learning_rate * v5、均方差损失函数
MSE:均方差损失函数。
# 损失函数的设计延续了Layer的模式,但是因为需要注意的是forward和backward部分有些不同
# MSE_loss = (predict_value - label) ^ 2
# MSE方法和Layer的区别:
# forward:y是组网输出的值,target是目标值(这里的输入是组网的输出和目标值),前向传播的同时把dloss / dy 计算出来
# backward: 没有参数,因为在forward的时候,计算出了dloss / dy,所以这里不需要输入参数
class MSE(Layer):
"""
Mean Square Error:
J = 0.5 * (y - target)^2
gradient formula:
dJ/dy = y - target
"""
def __init__(self, name='mse', reduction='mean', *args, **kwargs):
super().__init__(name=name, *args, **kwargs)
assert reduction in ['mean', 'none', 'sum'], "reduction only support 'mean', 'none' and 'sum', but got {}.".format(reduction)
self.reduction = reduction
self.pred = None
self.target = None
def forward(self, y, target):
assert y.shape == target.shape, "The shape of y and target is not same, y shape = {} but target shape = {}".format(y.shape, target.shape)
self.pred = y
self.target = target
loss = 0.5 * np.square(y - target)
if self.reduction is 'mean':
return loss.mean()
elif self.reduction is 'none':
return loss
else:
return loss.sum()
def backward(self):
gradient = self.pred - self.target
return gradient6、Dataset
tensorflow/pytorch/paddlepaddle都有Dataset类,这里也简单实现一个Dataset类。
# 这里仿照PaddlePaddle,Dataset需要实现__getitem__和__len__方法
class Dataset:
def __init__(self, *args, **kwargs):
pass
def __getitem__(self, idx):
raise NotImplementedError("'{}' not implement in class {}"
.format('__getitem__', self.__class__.__name__))
def __len__(self):
raise NotImplementedError("'{}' not implement in class {}"
.format('__len__', self.__class__.__name__))
# 根据dataset和一些设置,生成每个batch在dataset中的索引
class BatchSampler:
def __init__(self, dataset=None, shuffle=False, batch_size=1, drop_last=False):
self.batch_size = batch_size
self.drop_last = drop_last
self.shuffle = shuffle
self.num_data = len(dataset)
if self.drop_last or (self.num_data % batch_size == 0):
self.num_samples = self.num_data // batch_size
else:
self.num_samples = self.num_data // batch_size + 1
indices = np.arange(self.num_data)
if shuffle:
np.random.shuffle(indices)
if drop_last:
indices = indices[:self.num_samples * batch_size]
self.indices = indices
def __len__(self):
return self.num_samples
def __iter__(self):
batch_indices = []
for i in range(self.num_samples):
if (i + 1) * self.batch_size <= self.num_data:
for idx in range(i * self.batch_size, (i + 1) * self.batch_size):
batch_indices.append(self.indices[idx])
yield batch_indices
batch_indices = []
else:
for idx in range(i * self.batch_size, self.num_data):
batch_indices.append(self.indices[idx])
if not self.drop_last and len(batch_indices) > 0:
yield batch_indices
# 根据sampler生成的索引,从dataset中取数据,并组合成一个batch
class DataLoader:
def __init__(self, dataset, sampler=BatchSampler, shuffle=False, batch_size=1, drop_last=False):
self.dataset = dataset
self.sampler = sampler(dataset, shuffle, batch_size, drop_last)
def __len__(self):
return len(self.sampler)
def __call__(self):
self.__iter__()
def __iter__(self):
for sample_indices in self.sampler:
data_list = []
label_list = []
for indice in sample_indices:
data, label = self.dataset[indice]
data_list.append(data)
label_list.append(label)
yield np.stack(data_list, axis=0), np.stack(label_list, axis=0)三、线性回归实战
生成一组数据,利用上面完成的类,实现线性回归。
import matplotlib.pyplot as plt
class LinearDataset(Dataset):
def __init__(self, X, Y):
self.X = X
self.Y = Y
def __len__(self):
return len(self.X)
def __getitem__(self, idx):
return self.X[idx], self.Y[idx]
num_data = 200 # 训练数据数量
val_number = 500 # 验证数据数量
epoches = 500
batch_size = 4
learning_rate = 0.01
X = np.linspace(-np.pi, np.pi, num_data).reshape(num_data, 1)
Y = np.sin(X) * 2 + (np.random.rand(*X.shape) - 0.5) * 0.1
y_ = np.sin(X) * 2
model = Sequential(
Linear(1, 16, name='linear1'),
ReLU(name='relu1'),
Linear(16, 64, name='linear2'),
ReLU(name='relu1'),
Linear(64, 16, name='linear2'),
ReLU(name='relu1'),
Linear(16, 1, name='linear2'),
)
opt = SGD(parameters=model.parameters(), learning_rate=learning_rate, weight_decay=0.0, decay_type='l2')
loss_fn = MSE()
train_dataset = LinearDataset(X, Y)
train_dataloader = DataLoader(train_dataset, shuffle=True, batch_size=4, drop_last=True)
for epoch in range(1, epoches):
for x, y in train_dataloader:
pred = model(x)
loss = loss_fn(pred, y)
grad = loss_fn.backward()
model.backward(grad)
opt.step()
opt.clear_grad()
print("epoch: {}. loss: {}".format(epoch, loss))
X_val = np.linspace(-np.pi, np.pi, val_number).reshape(val_number, 1)
Y_val = np.sin(X_val) * 2
val_dataset = LinearDataset(X_val, Y_val)
val_dataloader = DataLoader(val_dataset, shuffle=False, batch_size=2, drop_last=False)
all_pred = []
for x, y in val_dataloader:
pred = model(x)
all_pred.append(pred)
all_pred = np.vstack(all_pred)
plt.scatter(X, Y, marker='x')
plt.plot(X_val, all_pred, color='red')
plt.show()四、实验结果
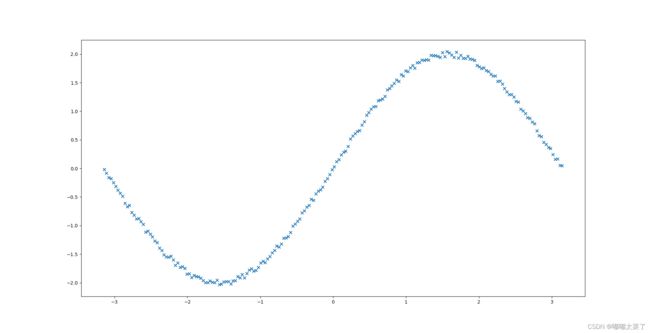
实验数据如图所示:
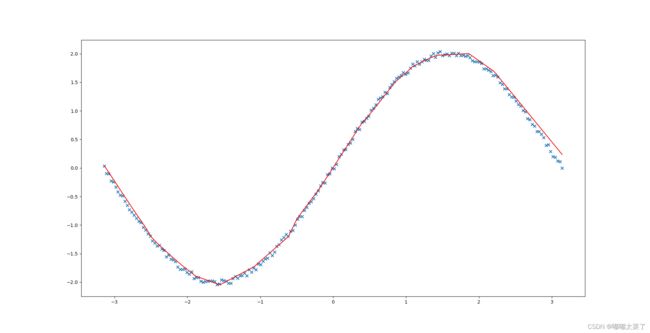
拟合结果如图所示,可以看出本文实现的神经网络模型拟合效果。
五、总结
深度学习理论简单,而且成熟的框架很多,大部分深度学习框架的使用者都不需要关注框架底层的实现。本文使用python的numpy库实现了一个非常简单的神经网络模型,并且验证了该模型在线性回归问题上的效果,相信你一定能有所收获。
代码运行不起来?在线notebook体验链接:【深度学习实战】一、Numpy手撸神经网络实现线性回归