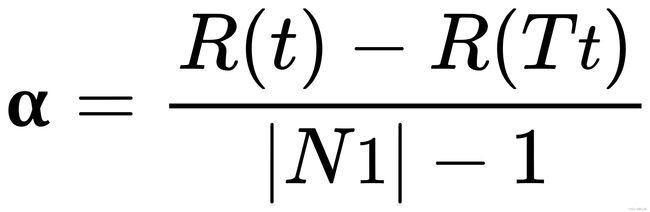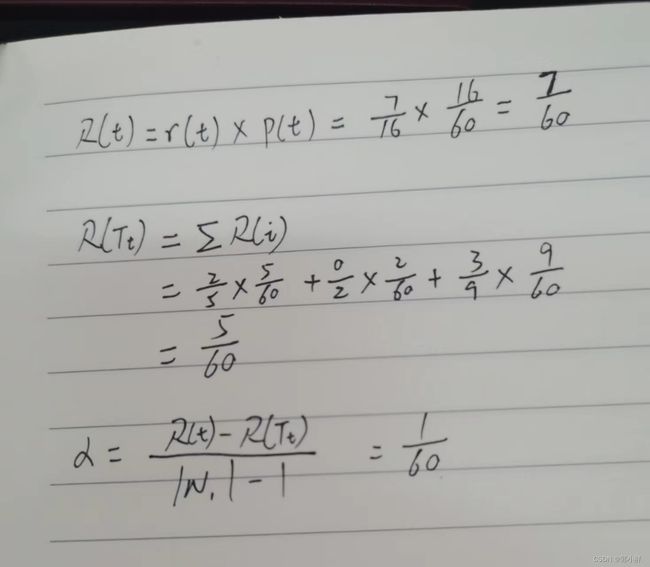决策树学习(二)
目录
连续值处理
剪枝操作
预剪枝
后剪枝
CCP代价复杂度剪枝:
剪枝结果展示:
预剪枝操作结果试验
后剪枝操作结果试验(CCP)
连续值处理
当特征值是连续值时,先将该特征所有值进行一个排序,然后再不断的二分,分成两部分数据,计算它们的熵值和信息增益
对于每种切分都计算他们的信息增益,观察在哪个地方切分的效果最好,就以那个点为区分的点,将连续的数据分成两部分
其实就可以理解为把连续值变成离散值来处理了
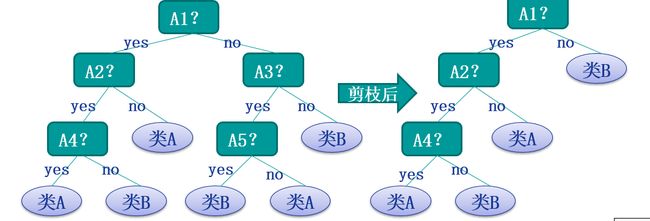
剪枝操作
剪枝的目的是为了防止过拟合情况的发生,在决策树模型训练的过程中为了尽可能的正确的分类训练样本从而不停的分裂结点,就会出现过拟合的情况,这时候就需要剪枝操作来减少决策树的分支。剪枝操作具体分为预剪枝和后剪枝。
预剪枝
预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛化性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点。
我们可以通过设置树的最大深度和结点数来提前进行限制从而达到预剪枝的效果。
预剪枝的方法:
1、限制树的深度。
2、限制结点数,当结点的样本数量大于某个阈值剪枝。
3、当信息增益、信息增益率或者基尼系数大于某个阈值剪枝。
4、当测试样本的正确性能够提升则剪枝。
后剪枝
后剪枝就是先构造一颗完整的决策树,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛华性能的提升,则把该子树替换为叶结点。
它首先构造完整的决策树,允许树过度拟合训练数据,然后对那些置信度不够的结点子树用叶子结点来代替,该叶子的类标号用该结点子树中最频繁的类标记。相比于先剪枝,这种方法更常用,正是因为在先剪枝方法中精确地估计何时停止树增长很困难。
以上可以理解为后剪枝的基本思想,其中后剪枝方法主要有以下几个方法:
Reduced-Error Pruning(REP,错误率降低剪枝)
Pesimistic-Error Pruning(PEP,悲观错误剪枝)
Cost-Complexity Pruning(CCP,代价复杂度剪枝)
EBP(Error-Based Pruning)(基于错误的剪枝)
这里详细介绍一下CCP代价复杂度剪枝
CCP代价复杂度剪枝:
该算法为子树Tt定义了代价(cost)和复杂度(complexity),以及一个可由用户设置的衡量代价与复杂度之间关系的参数α,其中,代价指在剪枝过程中因子树Tt被叶节点替代而增加的错分样本,复杂度表示剪枝后子树Tt减少的叶结点数,α则表示剪枝后树的复杂度降低程度与代价间的关系,定义为:
其中,
|N1|:子树Tt中的叶节点数;
R(t):结点t的错误代价,计算公式为R(t)=r(t)*p(t),r(t)为结点t的错分样本率,p(t)为落入结点t的样本占所有样本的比例;
R(Tt):子树Tt错误代价,计算公式为R(Tt)=∑R(i),i为子树Tt的叶节点。
CCP剪枝算法分为两个步骤:
1.对于决策树T的每个非叶结点计算α值,循环剪掉具有最小α值的子树,直到剩下根节点。在该步可得到一系列的剪枝树{T0,T1,T2......Tn},其中T0为原有的完全决策树,Tn为根结点,T1为对T0进行剪枝的结果,以此类推。
2.从子树序列中,根据真实的误差估计选择最佳决策树。
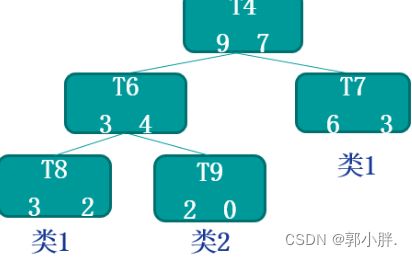
举个例子:
以结点T4为例,假设已有数据有六十条,那么
可得α=1/60
剪枝结果展示:
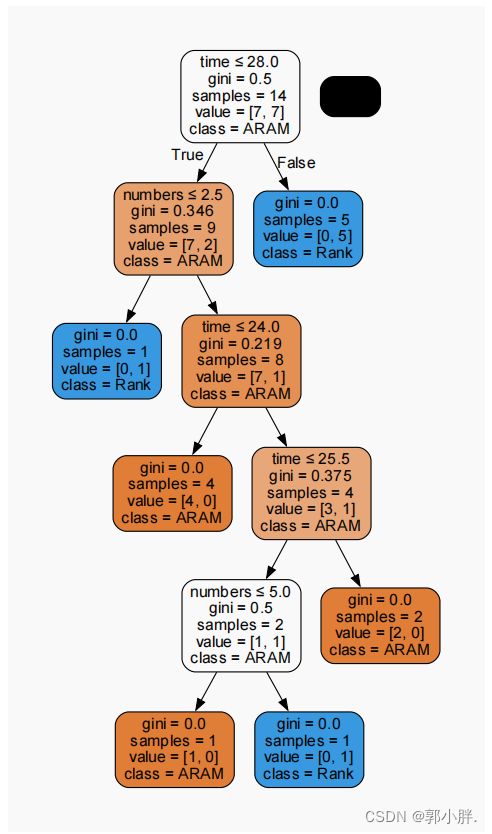
完全决策树(未剪枝)
第三层之后可以看到该决策树有点过拟合了,所以将树的最大深度设置为3层并观察结果。
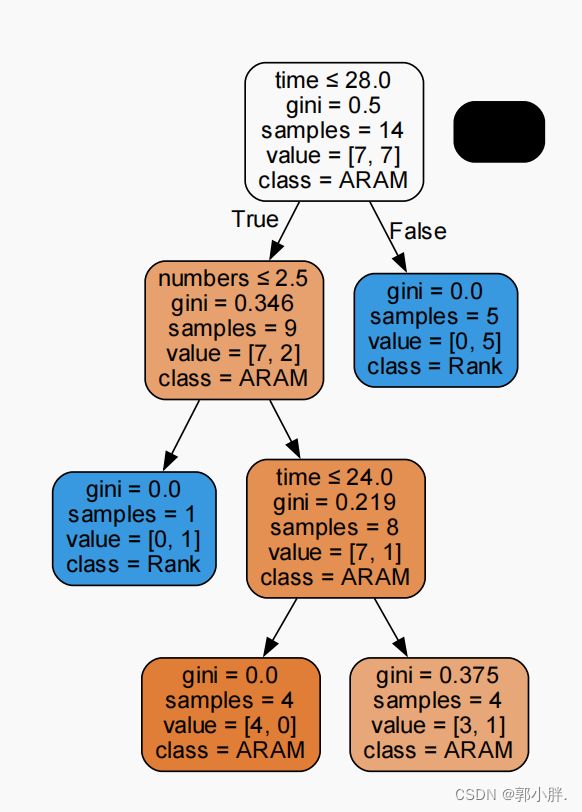
预剪枝操作结果试验
设置树的最大深度为3,max_depth=3。
tree_model = tree.DecisionTreeClassifier(criterion='gini',
max_depth=3,
min_samples_leaf=1,
ccp_alpha=0.0)结果:
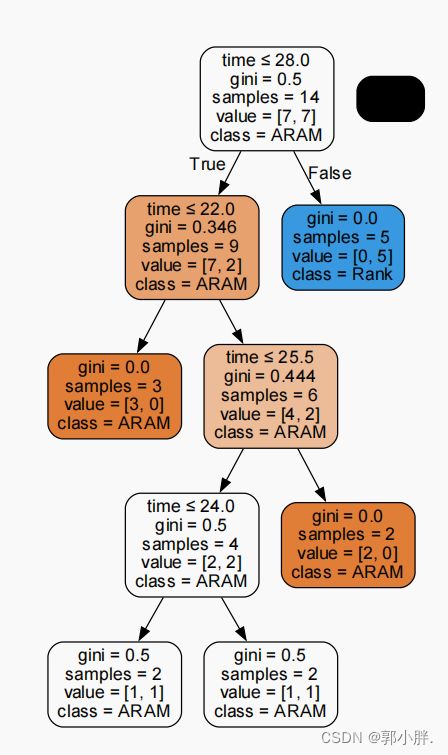
再修改一下叶子节点上的最小样本数量,从原来的1修改为2,结果如下
最下层几个节点的基尼系数都有点大,模型训练的不太好,所以min_samples_leaf的值还是设置为1更好。
后剪枝操作结果试验(CCP)
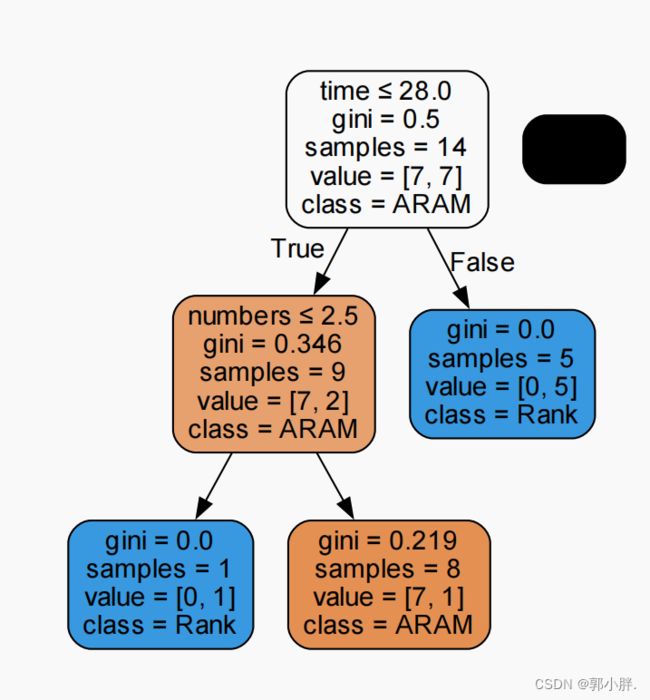
观察构建出来的决策树
以上图中的白色结点为例,计算它的α值
R(t)=1/2 * 2/14 = 1/14
R(Tt)=0/1 * 1/14 + 0/1 * 1/14 = 0
|N1| = 2
α = 1/14 约等于 0.07
调整代码中的ccp_alpha数值进行剪枝操作
具体代码
from sklearn import tree
import numpy as np
from io import StringIO
import pydotplus
# 导入数据
X = np.array([[3, 29, 1], [2, 31, 0], [1, 23, 0], [6, 21, 0],
[4, 25, 1], [5, 30, 1], [9, 18, 0], [8, 20, 1],
[3, 34, 1], [6, 23, 1], [5, 26, 1], [6, 25, 1],
[4, 31, 0], [7, 27, 0]])
y = np.array([[1], [1], [1], [0], [0],
[1], [0], [0], [1], [0],
[0], [1], [1], [0]])
# 构建决策树
tree_model = tree.DecisionTreeClassifier(criterion='gini',
max_depth=None,
min_samples_leaf=1,
ccp_alpha=0.07)
# 训练模型
tree_model.fit(X, y)
# 可视化操作
dot_data = StringIO()
feature_names = ['numbers', 'time', 'talk']
target_names = ['ARAM', 'Rank']
tree.export_graphviz(tree_model,
out_file=dot_data,
feature_names=feature_names,
class_names=target_names,
filled=True,
rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf("tree5.pdf")
# 预测数据
x = np.array([[5, 20, 1]])
print(tree_model.predict(x))
x2 = np.array([[4, 29, 1]])
print(tree_model.predict(x2))