YOLOV3论文详解
本文主要介绍了YOLOV3的网络结构和损失函数,其他部分几乎与YOLOV2相差无几。
YOLOV3算法Pytorch实现:https://github.com/codecat0/CV/tree/main/Object_Detection/YOLOV3
1. Introduction
2. The Deal
2.1 Bounding Box Prediction
在YOLOV2后,我们的系统开始使用聚类来确定anchor的尺寸和比例。网络会为每一个bounding box预测4个坐标: t x , t y , t w , t h t_x,t_y,t_w,t_h tx,ty,tw,th。如果网格单元相对于图像的左上角的偏移为哦 ( c x , c y ) (c_x,c_y) (cx,cy),而且anchor的宽高为 p w , p h p_w,p_h pw,ph,那么对应的预测值为:
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t h b_x=\sigma(t_x)+c_x \\ b_y=\sigma(t_y)+c_y \\ b_w=p_we^{t_w} \\ b_h=p_he^{t_h} bx=σ(tx)+cxby=σ(ty)+cybw=pwetwbh=pheth
在训练期间,我们采用均方误差作为损失函数。anchor的坐标信息: ( c x , c y , p w , p h ) (c^x,c^y,p^w,p^h) (cx,cy,pw,ph),预测框的坐标信息: ( b x , b y , b w , b h ) (b^x,b^y,b^w,b^h) (bx,by,bw,bh),真实框的坐标信息: ( g x , g y , g w , g h ) (g^x,g^y,g^w,g^h) (gx,gy,gw,gh), l l l表示预测框与anchor的偏移量, g g g表示真实框与anchor的偏移量。那么损失函数定义如下:
L l o c = ∑ i ∈ p o s ∑ m ∈ { x , y , w , h } ( l i m − g i m ) 2 l i x = b i x − c i x , l i y = b i y − c i y l i w = l o g ( b i w / p i w ) , l i h = l o g ( b i h / p i h ) g i x = g i x − c i x , g i y = g i y − c i y g i w = l o g ( g i w / p i w ) , g i h = l o g ( g i h / p i h ) L_{loc}=\sum_{i \in pos}\sum_{m \in \{x,y,w,h\}}(l_i^m - g_i^m)^2 \\ l_i^x = b_i^x - c_i^x, \quad l_i^y = b_i^y - c_i^y \\ l_i^w = log(b_i^w / p_i^w), \quad l_i^h=log(b_i^h / p_i^h) \\ g_i^x = g_i^x - c_i^x, \quad g_i^y = g_i^y - c_i^y \\ g_i^w = log(g_i^w / p_i^w), \quad g_i^h=log(g_i^h / p_i^h) Lloc=i∈pos∑m∈{x,y,w,h}∑(lim−gim)2lix=bix−cix,liy=biy−ciyliw=log(biw/piw),lih=log(bih/pih)gix=gix−cix,giy=giy−ciygiw=log(giw/piw),gih=log(gih/pih)
上式中w、h的均方损失可以对其取平方根与YOLOV1一样,达到对小目标增加权重的效果,毕竟小目标偏移一点相对于大目标偏移一点误差应该更大才对
YOLOV3用逻辑回归预测每一个预测框的置信度,即预测框内是否存在目标的概率。我们为每一个GT box分配一个anchor,如果一个anchor没有被分配给相应GT box,那么该anchor没有目标定位损失和目标类别损失,只有置信度损失。(如果一个未分配GT box的anchor与其他GT box的IOU值超出某一个阈值,我们会忽视它,这个阈值为0.5)。 o i ∈ { 0 , 1 } o_i \in \{0,1\} oi∈{0,1}表示预测框 i i i中是否真实存在目标, c ^ i \hat c_i c^i表示预测框 i i i内存在目标的 S i g m o i d Sigmoid Sigmoid概率,其置信度损失如下所示:
L c o n f ( o , c ) = − ∑ ( o i l n ( c ^ i ) + ( 1 − o i ) l n ( 1 − c ^ i ) ) c ^ i = S i g m o d ( c i ) L_{conf}(o,c)=-\sum(o_iln(\hat c_i)+(1-o_i)ln(1-\hat c_i)) \\ \hat c_i = Sigmod(c_i) Lconf(o,c)=−∑(oiln(c^i)+(1−oi)ln(1−c^i))c^i=Sigmod(ci)
2.2 Class Prediction
类别预测方面主要是将原来的单标签分类改进为多标签分类,因此网络结构上就将原来用于单标签多分类的 softmax 层换成用于多标签多分类的逻辑回归层。
首先说明一下为什么要做这样的修改,原来分类网络中的 softmax 层都是假设一张图或一个 object只属于一个类别,但是在一些复杂场景下,一个 object 可能属于多个类,比如有的类别中有woman和 person 两个类,这就是多标签分类,需要用逻辑回归层来对每个类别做二分类。逻辑回归层主要用到 Sigmoid函数,该函数可以将输入约束在0~1的范围内,因此当一张图片经过特征提取后的某一类输出经过Sigmoid 函数约束后如果大于 0.5, 就表示属于该类。
对于类别损失,我们使用二值交叉熵损失函数。其中 O i j ∈ { 0 , 1 } O_{ij} \in \{0,1\} Oij∈{0,1}表示预测框 i i i是否真实存在第 j j j类目标, C ^ i j \hat C_{ij} C^ij表示预测框 i i i存在第 j j j类目标的 S i g m o i d Sigmoid Sigmoid概率
L c l s ( O , C ) = − ∑ i ∈ p o s ∑ j ∈ c l s ( O i j l n ( C ^ i j ) + ( 1 − O i j ) l n ( 1 − C ^ i j ) ) C ^ i j = S i g m o i d ( C i j ) L_{cls}(O,C)=-\sum_{i \in pos} \sum_{j \in cls}(O_{ij}ln(\hat C_{ij}) + (1 - O_{ij})ln(1-\hat C_{ij})) \\ \hat C_{ij} = Sigmoid(C_{ij}) Lcls(O,C)=−i∈pos∑j∈cls∑(Oijln(C^ij)+(1−Oij)ln(1−C^ij))C^ij=Sigmoid(Cij)
2.3 Predictions Across Scales
YOLOV3采用了类似FPN网络提取了3个不同尺度的特征,与FPN不同的是在进行不同尺度特征融合时不是像FPN采用相加而是采用concatenate拼接,最后融合了3个scale,分别是13x13、26x26和52x52,并在这3个scale的特征图进行检测。下文会有详细的网络结构图。
和YOLOV2一样,YOLOV3使用的聚类方法还是K-Means,它能用来确定边界框的先验。在实验中,我们选择了9个聚类和3个尺寸,然后在不同尺寸的边界框上均匀分割维度聚类。在COCO数据集上,这9个聚类分别是:(10×13)、(16×30)、(33×23)、(30×61)、(62×45)、(59×119)、(116 × 90)、(156 × 198)、(373 × 326)。
2.4 Feature Extractor
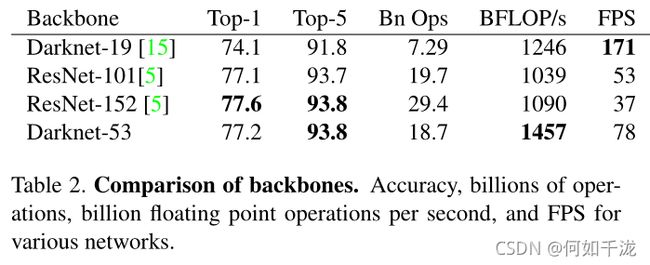
我们使用一个新的网络来提取特征,它融合了YOLOV2,Darknet-19以及其他新型残差网络,由连续的3x3和1x1卷积层组合而成,当然,其中也添加了一些shortcut connection,因为一共有53个卷积层,所以我们称它 Darknet-53。

这个新网络性能上远超DarkNet-19,准确性与ResNet-101和ResNet-152差不多,但效率更高。