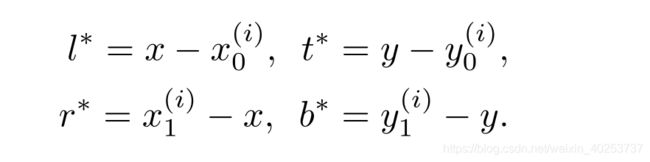FCOS_ Fully Convolutional One-Stage Object Detection 论文笔记
background
任务:改变目标检测中边框的提供方法,降低计算量
关键词: Feature Pyramid , Center-ness,Multi-level Prediction with FPN for FCOS
Introduction
以faster rcnn为例, 基于anchor boxes产生预测框,然后做回归任务,但为了增大iou,选择了生成大量的预测框,其中大部分是无效的,过多的无效边框只会增大算力的负担,而且还会影响最终的训练效果,并且预测框的超参数的设置,很大程度上影响最终模型的效果,虽然有边框的微调,但是对于一些其他环境中的检测,微调的效果可能很差,而且边框大多数是固定住的,对于回归任务,边框敏感的任务来说,使模型的准确率降低不少,需要经过细心的调试,并且使用了非最大值抑制的方法,其中的并交比的设置也十分影响模型的准确性。
所以作者提出了一种不基于anchor boxes的方式来产生边框,并且边框的数目和计算开销都有了不错的降低,而且效果也不错
模型的主要思路是,先利用特征金字塔,产生不同分辨率下的feature maps,对于低分辨率的feature maps鲁棒性更强,主要负责图片中较大的物体的预测,而分辨率的feature maps主要负责图片中较小的物体的预测,不同分辨率下的预测边框互不干扰,最后通过shared heads对建议区域进行操作,产生box的预测,种类预测,和center-ness,center-ness主要是对最后的box的加权求和(因为论文作者取消了非最大值抑制的方法,对于非最大值抑制确实要消耗很高的算力,主要通过IOU进行比较的话,时间上的开销都很大)
Model
整体的结构

这里的P6,P7是P5通过stride为2的卷积依次产生的
Head是一个head 共享的,这样可以有效减少参数的引入,但不同分辨率下的输入,需要通过一个可学习的S矩阵来对他进行微调。
Fully Convolutional One-Stage Object Detector
对于实际的目标区域,由左上和右下的点确定
B i = ( x 0 ( i ) , y 0 ( i ) , x 1 ( i ) , y 1 ( i ) , c ( i ) ) B_{i}=(x_0^{(i)},y_0^{(i)},x_1^{(i)},y_1^{(i)},c^{(i)}) Bi=(x0(i),y0(i),x1(i),y1(i),c(i))
其中前四个为目标边框的左上,右下坐标, c ( i ) c^{(i)} c(i)是目标的种类(如果点落入到背景中,则C=0),对于feature maps上的坐标(x,y),映射到输入的图片中为 ( [ s 2 ] + s x , [ s 2 ] + s y ) ([\frac{s}{2}]+sx,[\frac{s}{2}]+sy) ([2s]+sx,[2s]+sy)
s是降采样的比例。
所以得到 t ∗ = ( l ∗ , t ∗ , r ∗ , b ∗ ) t^{*}=(l^{*},t^{*},r^{*},b^{*}) t∗=(l∗,t∗,r∗,b∗)
Network Outputs
如上图最后的会产生Regression(WH4),得到每个点对应的向量 t = ( l , t , r , b ) t=(l,t,r,b) t=(l,t,r,b),将此向量与 t ∗ t^{*} t∗做回归,并且回归任务映射到 e x p ( x ) exp(x) exp(x)中
Loss Function
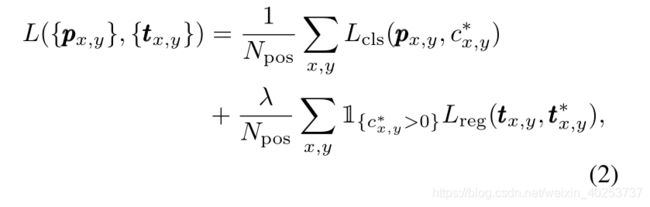
P x , y > 0.05 记 为 正 样 本 P_{x,y}>0.05记为正样本 Px,y>0.05记为正样本
N x , y N_{x,y} Nx,y是W*H
L c l s L_{cls} Lcls是预测种类的损失
L c l s L_{cls} Lcls下面的公式是对边框的预测损失
Multi-level Prediction with FPN for FCOS
上面的结构图,P6,P7是由P5,通过stride为2的卷积得到
对于从 p i p_{i} pi中映射到输入图片中的边框预测要求:
m a x ( l ∗ , t ∗ , r ∗ , b ∗ ) > m i max(l^{*},t^{*},r^{*},b^{*})>m_{i} max(l∗,t∗,r∗,b∗)>mi 或者 m a x ( l ∗ , t ∗ , r ∗ , b ∗ ) < m i − 1 max(l^{*},t^{*},r^{*},b^{*})
eg:
P3:[0,64],P4:[64,128]…
则将此点即为无效点,(因为不在自己的预测范围内)
如果在相同的范围内,有多个点,则选择画出面积最小的边框
Center-ness for FCOS
为了避免远离目标的低质量的框的出现
中心度:
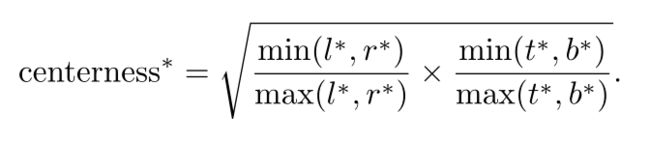
将网络预测的中心度与分类得分相乘,从而可以降低由远离目标中心位置预测的低质量边界框的权重。
Experiments
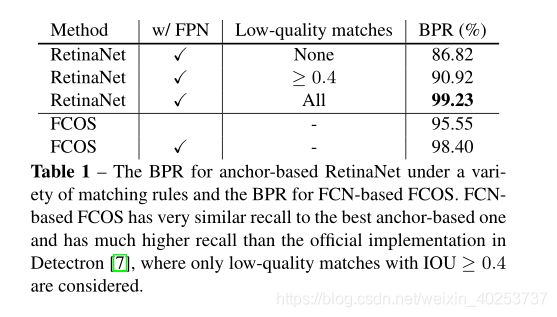
消融实验
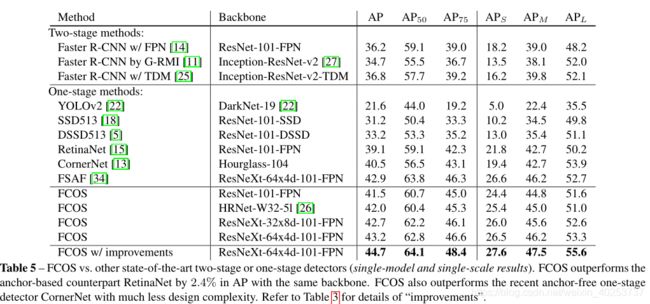
FCOS vs. Anchor-based Detectors
Learn from paper
通过不同分辨率下的feature maps将点映射到输入图片中,通过限制边框大小,来确定不同大小的边框,而且去除了边框的初始化,使得模型泛化能力变强,有利于模型的训练和适应更多的情况
计算量减少了不少,而且产生的边框的质量相比faster rcnn提升很多。
用center-ness代替NMS,这里也减少了很大的计算量。