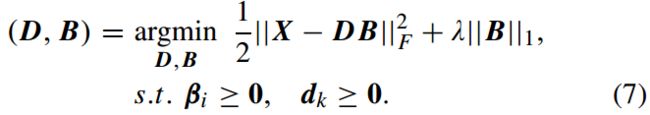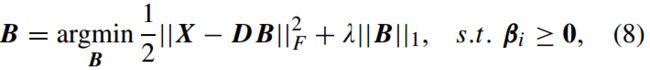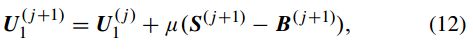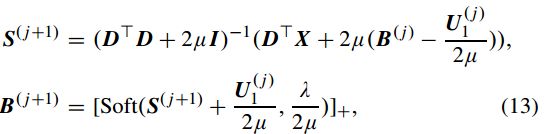- elementUI轮播图组件el-carousel适配移动端大小(图片加载好后根据大小适配)
printf_824
elementuijavascriptvue.js
获取img实例,动态设置el-carousel高度import{ref,onMounted,onBeforeUnmount,nextTick}from'vue';constbanners=ref(['/images/banner/banner1.png','/images/banner/banner1.png','/images/banner/banner1.png','/images/banne
- 一篇文章让你彻底明白AI编程遵循的MVP原则+AI实战。
飞算JavaAI开发助手
AIJava编程思想大数据
MVP顾名思义,最有价值球员(MostValuablePlayer),搞错了!再来。MVP最小可行产品(MinimumViableProduct),指通过实现核心功能并不断选代完成产品验证与升级。例如,一个大型商城项目会包含以下功能模块:XXX商城项目的核心模块解析3.01.用户中心模块核心功能:用户注册/登录、资料管理、账号安全(如二次验证)、收货地址管理、会员等级体系(VIP权益、积分规则)。
- Docker基本概念——AI教你学Docker
LuckyLay
docker容器运维
1.1Docker概念详解1.Docker是什么?Docker是一个开源的应用容器引擎,它让开发者可以将应用及其依赖打包到一个可移植的容器(Container)中,并在任何支持Docker的Linux、Windows或macOS系统上运行。这样做极大地提升了应用的可移植性、一致性和部署效率。2.核心概念2.1镜像(Image)镜像是一个只读的模板,包含了运行容器所需的程序、库、环境变量和配置文件等
- 基于OpenCV-python的人脸识别系统
transuperb
完整代码opencvpython人工智能
importsysimportosimporttkinterastkfromtkinter.ttkimportStyleimportnumpyasnpimportcv2fromPILimportImageTk,ImageDraw,ImageFontfrompanel.models.tabulatorimportthemefromModelimport*fromtkinterimportttk,fi
- Python视觉实战项目31讲源码地址
机械小蛟龙
笔记opencvpython深度学习
Python视觉实战项目31讲源码地址来源:公众号小白学视觉2月1日使用OpenCV实现猜词游戏https://github.com/spmallick/learnopencv/tree/master/Hangman使用OpenCV实现图像修复https://github.com/spmallick/learnopencv/tree/master/Image-Inpainting自适应显着性的图像
- Python创意爱心代码合集(7种实现方案)
我非常不满意
pythonpygame开发语言
方案一:动态粒子爱心(Pygame实现)importpygameimportmathimportrandompygame.init()W,H=1200,800screen=pygame.display.set_mode((W,H))particles=[]classParticle:def__init__(self):self.angle=random.uniform(0,2*math.pi)se
- 【力扣 中等 C】912. 排序数组
黑听人
c语言leetcode数据结构算法开发语言
目录题目解法一:快速排序解法二:归并排序题目解法一:快速排序voidswap(int*a,int*b){inttmp=*a;*a=*b;*b=tmp;}voidpartition(int*nums,intleft,intright,int*leftMax,int*rightMin){intrandomNum=nums[left+rand()%(right-left+1)];intl=left,r=
- Milvus中 Collections 级多租户 和 分区级多租户 的区别
背太阳的牧羊人
人工智能RAG优化方法milvus向量数据库
原文链接图片内容中。1,所有租户共用一个Collection:所有租户共享一个Collection,租户特定字段用于过滤。2,每个租户一个分区:租户共享一个Collections,但他们的数据存储在不同的分区中。我们可以通过为每个租户分配一个专用分区来隔离数据。3,基于PartitionKey的多租户:这是一种可扩展性更强的方案,其中单个Collections使用分区Key来区分租户。它们看起来相
- 【uniapp】给图片添加水印
改bug的101天
uniappuni-appvue.js前端
1、创建画布varcontext=uni.createCanvasContext('Canvas')2、获取本地图片uni.chooseImage({count:1,success:(res)=>{varfile=res.tempFilePaths[0];consttempFiles=res.tempFiles[0]})})3、获取图片信息----添加水印uni.getImageInfo({src
- Fast Image Deconvolution using Hyper-Laplacian Priors论文阅读
青铜锁00
#退化论文阅读论文阅读图像处理
FastImageDeconvolutionusingHyper-LaplacianPriors1.论文的研究目标与实际意义2.论文的创新方法2.1核心框架:交替最小化(AlternatingMinimization)2.2x子问题:频域FFT加速2.3w子问题:高效求解的核心创新2.3.1问题形式2.3.2查找表法(LUT)2.3.3解析解法(特定α\alphaα)2.3.4通用α\alphaα
- [arXiv 2024] Medical SAM 2: Segment Medical Images as Video via Segment Anything Model 2
alfred_torres
医学图像分割SAM2
arXiv2024|MedicalSAM2:通用2D/3D医学分割新范式,“把医学图像当视频分割”论文信息标题:MedicalSAM2:SegmentMedicalImagesasVideoviaSegmentAnythingModel2作者:JiayuanZhu,AbdullahHamdi,YunliQi,YuemingJin,JundeWu单位:牛津大学、新加坡国立大学项目主页:https:/
- [CVPR 2025] 高效无监督Prompt与偏好对齐驱动的半监督医学分割
alfred_torres
prompt医学图像分割
CVPR2025|优化SAM:高效无监督Prompt与偏好对齐驱动的半监督医学分割论文信息标题:EnhancingSAMwithEfficientPromptingandPreferenceOptimizationforSemi-supervisedMedicalImageSegmentation作者:AishikKonwer,ZhijianYang,ErhanBas,CaoXiao,Pratee
- 图14CLIP 模型在 “分布偏移场景” 下的鲁棒性优化策略|学习笔记
学渣67656
笔记人工智能
一、先明确:左图的核心对比维度左图的横轴是“模型在标准分布上的准确率”,纵轴是“模型在分布偏移数据集上的准确率”,本质是对比“不同模型/策略在“标准性能”与“鲁棒性”之间的权衡,图中每条曲线代表一类模型/策略的“标准性能-鲁棒性”趋势,而红色箭头标注的“AdapttoImageNet”是一种“干预策略”,作用于CLIP模型后,使其性能点落在对应曲线上。二、左图中6条曲线的含义(按图例颜色+模型类型
- 前端ul-image的src接收base64快捷写法
peachSoda7
前端
前端ul-image的src接收base64快捷写法data:image/png;base64,你的base64数据注意如果是jpg就改成jpg,中间的逗号格式要注意,/注意不要反了假设后端返回的detail中的url已经是base64格式,下面是示例
- No module named ‘skimage‘的问题及解决
蓝天居士
AIpycharm
项目中执行importtorchxrayvisionasxrv时出现以下错误:Traceback(mostrecentcalllast):File"D:/研究生/毕业设计/COVID19/COVID19_CT/conduct.py",line14,inimporttorchxrayvisionasxrvFile"D:\研究生\毕业设计\COVID19\COVID19_CT\torchxrayvis
- 12.分割区域
Echo``
Halcon系统化学习前端图像处理c#人工智能机器学习计算机视觉
目录1.拆分相邻区域12.拆分相邻区域23.分体区域合并4.正反检测5.芯片除尘1.拆分相邻区域1*Thisprogramsdemonstratestheuseofbasicmorphology*operators.*Theaimoftheprogramistodetecteachsinglepellet*(brightparticleonadarkerbackground).*dev_updat
- GaussDB SQL基础语法示例:BOOLEAN表达式详解
喜酱的探春
gaussdbsqltensorflow数据库
GaussDBSQL基础语法示例:BOOLEAN表达式详解BOOLEAN表达式是SQL中实现逻辑判断的核心工具,用于组合多个条件或处理真值判断。本文将结合GaussDB特性,通过实际场景解析其用法与最佳实践。一、基础语法结构简单条件组合--AND并列条件SELECT*FROMemployeesWHEREdepartment='IT'ANDsalary>10000;--OR选择条件SELECTpro
- java鱼眼相机标定_鱼眼相机标定以及OpenCV实现
元宿six
java鱼眼相机标定
开始标定doublefisheye::calibrate(InputArrayOfArraysobjectPoints,InputArrayOfArraysimagePoints,constSize&image_size,InputOutputArrayK,InputOutputArrayD,OutputArrayOfArraysrvecs,OutputArrayOfArraystvecs,int
- Halcon 检测物体定位点
吃个糖糖
Halcon人工智能计算机视觉深度学习
文章目录get_domain返回所有输入图像的定义域作为一个区域add_channels给区域增加灰度值find_shape_model发现匹配模板find_shape_models发现最佳模板示例get_domain返回所有输入图像的定义域作为一个区域Halcon中的区域get_domain(Image:Domain::)Image:图像(input_object):类型可以是(多通道-)图像数
- Halcon中如何对特定目标进行定位查找
极客晨风
#Halcon例程项目讲解计算机视觉人工智能图像处理Halconc++
一、项目代码下载项目的完整代码可以通过以下链接进行下载:通过网盘分享的文件:垫片查找.7z链接:https://pan.baidu.com/s/1cexsR99mMWcC2v0k0MJ5LQ?pwd=jkcf提取码:jkcf二、算法流程图像预处理:首先,通过read_image函数读取图像,并利用fast_threshold函数进行图像的阈值化处理。阈值化后的图像会提取出强度值在特定范围内的区域,
- C#仿CANoe设计面板PANL的设计思路
99乘法口诀万物皆可变
C#c#单片机stm32
usingSystem;usingSystem.Windows.Forms;usingUTS_Link_CANoe_Bridge.VariableManagerEnhanced;namespaceUTS_Link_CANoe_Bridge{publicpartialclassVariableManagerEnhanced_UIDebug:Form{publicVariableManagerEnha
- laravel中图片路径失效图片不显示的解决方法
一秒公司
laravelphp
先将目录public下的storage删除(这是个软链接,如果双击会提示错误路径),注意:操作前记得备份!!!然后在项目目录下运行命令行:phpartisanstorage:link运行结果如下图后
- RuntimeError: Unsupported image type, must be 8bit gray or RGB image.
Roc-xb
Pythonpythoncv2opencv
(face)E:\code\运行代码>C:/Users/29847/Anaconda3/envs/face/python.exee:/code/运行代码/face.pyTraceback(mostrecentcalllast):File“e:\code\运行代码\face.py”,line76,insuccess=registrator.register_face(“Mark_Zuckerberg
- C#-获取屏幕分辨率
dxm809
C#
usingSystem;usingSystem.Collections.Generic;usingSystem.ComponentModel;usingSystem.Data;usingSystem.Drawing;usingSystem.Text;usingSystem.Windows.Forms;namespaceGetScreenSize{publicpartialclassFrm_Main
- Laravel 项目中图片上传后无法访问的问题
TO_WebNow
Laravellaravelphp
情况:Laravel提供了phpartisanstorage:link命令,用于创建符号链接(SymbolicLink),将storage/app/public映射到public/storage。但是上传图片之后文件目录确实有但是无法访问。1.删除已经创建的rm-rfpublic/storage2.重新创建符号链接:phpartisanstorage:link3.检查符号链接是否正确:ls-lpu
- 【AI时代生死局】Python程序员如何靠这3招逆天改命?(附免费转型资源包)
骆驼_代码狂魔
程序员的生存人工智能python开发语言决策树
开篇暴击:程序员正在经历的「降维打击」https://via.placeholder.com/600x300?text=AI%E5%8F%96%E4%BB%A3%E4%BA%BA%E7%B1%BB%E7%BC%96%E7%A8%8B%E8%BF%9B%E5%BA%A6%E8%A1%A8"当你还在纠结Python语法时,AI已经能3秒生成整个电商系统..."(用具体数据增强可信度:GitHubCop
- Linux Sonic Agent 端部署(详细版)(腾讯云)
被困者
Soniclinux服务器运维
(因为服务器是Linux的,只是安装了,并没有验证)1、编辑docker-compose.yml文件在Services下添加Agentsonic-agent:image:"sonicorg/sonic-agent-linux:v2.7.2"environment:-SONIC_SERVER_HOST=${SONIC_SERVER_HOST}-SONIC_SERVER_PORT=${SONIC_SE
- 前端截图并导出pdf
半糖1122
前端pdf
实践使用domtoimage和domToPdf说明:1需要将页面的一个流程图导出2要求导出成pdf,且pdf上有标题等内容做法:因为导出的pdf中包含不存在页面上的内容需要先将流程图截图成图片,再生成dom节点,之后导出成pdf代码实现:importdomtoimagefrom'dom-to-image';importdomToPdffrom'dom-to-pdf';exportToPngDire
- openmv入门(三)
做好自己吧!
openmv人工智能python嵌入式硬件opencv
一ApilTagimportsensor,time,image,math#设置摄像头sensor.reset()sensor.set_pixformat(sensor.RGB565)sensor.set_framesize(sensor.QQVGA)#分辨率,像素点sensor.set_auto_gain(False)sensor.set_auto_whitebal(False)sensor.se
- 【Unity关于Windows文件的一些常用操作1】
灬悟空不悟灬
Unity小技巧unity游戏引擎
Unity关于Windows文件的一些常用操作本人项目中遇到的一些Unity关于Windows文件的一些常用操作。以后还会继续进行扩展。usingSystem;usingSystem.IO;usingSystem.Linq;usingUnityEngine;namespaceWKFrame.Controller{publicpartialclassUtils:Singleton{//////清空文
- scala的option和some
矮蛋蛋
编程scala
原文地址:
http://blog.sina.com.cn/s/blog_68af3f090100qkt8.html
对于学习 Scala 的 Java™ 开发人员来说,对象是一个比较自然、简单的入口点。在 本系列 前几期文章中,我介绍了 Scala 中一些面向对象的编程方法,这些方法实际上与 Java 编程的区别不是很大。我还向您展示了 Scala 如何重新应用传统的面向对象概念,找到其缺点
- NullPointerException
Cb123456
androidBaseAdapter
java.lang.NullPointerException: Attempt to invoke virtual method 'int android.view.View.getImportantForAccessibility()' on a null object reference
出现以上异常.然后就在baidu上
- PHP使用文件和目录
天子之骄
php文件和目录读取和写入php验证文件php锁定文件
PHP使用文件和目录
1.使用include()包含文件
(1):使用include()从一个被包含文档返回一个值
(2):在控制结构中使用include()
include_once()函数需要一个包含文件的路径,此外,第一次调用它的情况和include()一样,如果在脚本执行中再次对同一个文件调用,那么这个文件不会再次包含。
在php.ini文件中设置
- SQL SELECT DISTINCT 语句
何必如此
sql
SELECT DISTINCT 语句用于返回唯一不同的值。
SQL SELECT DISTINCT 语句
在表中,一个列可能会包含多个重复值,有时您也许希望仅仅列出不同(distinct)的值。
DISTINCT 关键词用于返回唯一不同的值。
SQL SELECT DISTINCT 语法
SELECT DISTINCT column_name,column_name
F
- java冒泡排序
3213213333332132
java冒泡排序
package com.algorithm;
/**
* @Description 冒泡
* @author FuJianyong
* 2015-1-22上午09:58:39
*/
public class MaoPao {
public static void main(String[] args) {
int[] mao = {17,50,26,18,9,10
- struts2.18 +json,struts2-json-plugin-2.1.8.1.jar配置及问题!
7454103
DAOspringAjaxjsonqq
struts2.18 出来有段时间了! (貌似是 稳定版)
闲时研究下下! 貌似 sruts2 搭配 json 做 ajax 很吃香!
实践了下下! 不当之处请绕过! 呵呵
网上一大堆 struts2+json 不过大多的json 插件 都是 jsonplugin.34.jar
strut
- struts2 数据标签说明
darkranger
jspbeanstrutsservletScheme
数据标签主要用于提供各种数据访问相关的功能,包括显示一个Action里的属性,以及生成国际化输出等功能
数据标签主要包括:
action :该标签用于在JSP页面中直接调用一个Action,通过指定executeResult参数,还可将该Action的处理结果包含到本页面来。
bean :该标签用于创建一个javabean实例。如果指定了id属性,则可以将创建的javabean实例放入Sta
- 链表.简单的链表节点构建
aijuans
编程技巧
/*编程环境WIN-TC*/ #include "stdio.h" #include "conio.h"
#define NODE(name, key_word, help) \ Node name[1]={{NULL, NULL, NULL, key_word, help}}
typedef struct node { &nbs
- tomcat下jndi的三种配置方式
avords
tomcat
jndi(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。命名服务将名称和对象联系起来,使得我们可以用名称
访问对象。目录服务是一种命名服务,在这种服务里,对象不但有名称,还有属性。
tomcat配置
- 关于敏捷的一些想法
houxinyou
敏捷
从网上看到这样一句话:“敏捷开发的最重要目标就是:满足用户多变的需求,说白了就是最大程度的让客户满意。”
感觉表达的不太清楚。
感觉容易被人误解的地方主要在“用户多变的需求”上。
第一种多变,实际上就是没有从根本上了解了用户的需求。用户的需求实际是稳定的,只是比较多,也比较混乱,用户一般只能了解自己的那一小部分,所以没有用户能清楚的表达出整体需求。而由于各种条件的,用户表达自己那一部分时也有
- 富养还是穷养,决定孩子的一生
bijian1013
教育人生
是什么决定孩子未来物质能否丰盛?为什么说寒门很难出贵子,三代才能出贵族?真的是父母必须有钱,才能大概率保证孩子未来富有吗?-----作者:@李雪爱与自由
事实并非由物质决定,而是由心灵决定。一朋友富有而且修养气质很好,兄弟姐妹也都如此。她的童年时代,物质上大家都很贫乏,但妈妈总是保持生活中的美感,时不时给孩子们带回一些美好小玩意,从来不对孩子传递生活艰辛、金钱来之不易、要懂得珍惜
- oracle 日期时间格式转化
征客丶
oracle
oracle 系统时间有 SYSDATE 与 SYSTIMESTAMP;
SYSDATE:不支持毫秒,取的是系统时间;
SYSTIMESTAMP:支持毫秒,日期,时间是给时区转换的,秒和毫秒是取的系统的。
日期转字符窜:
一、不取毫秒:
TO_CHAR(SYSDATE, 'YYYY-MM-DD HH24:MI:SS')
简要说明,
YYYY 年
MM 月
- 【Scala六】分析Spark源代码总结的Scala语法四
bit1129
scala
1. apply语法
FileShuffleBlockManager中定义的类ShuffleFileGroup,定义:
private class ShuffleFileGroup(val shuffleId: Int, val fileId: Int, val files: Array[File]) {
...
def apply(bucketId
- Erlang中有意思的bug
bookjovi
erlang
代码中常有一些很搞笑的bug,如下面的一行代码被调用两次(Erlang beam)
commit f667e4a47b07b07ed035073b94d699ff5fe0ba9b
Author: Jovi Zhang <
[email protected]>
Date: Fri Dec 2 16:19:22 2011 +0100
erts:
- 移位打印10进制数转16进制-2008-08-18
ljy325
java基础
/**
* Description 移位打印10进制的16进制形式
* Creation Date 15-08-2008 9:00
* @author 卢俊宇
* @version 1.0
*
*/
public class PrintHex {
// 备选字符
static final char di
- 读《研磨设计模式》-代码笔记-组合模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
abstract class Component {
public abstract void printStruct(Str
- 利用cmd命令将.class文件打包成jar
chenyu19891124
cmdjar
cmd命令打jar是如下实现:
在运行里输入cmd,利用cmd命令进入到本地的工作盘符。(如我的是D盘下的文件有此路径 D:\workspace\prpall\WEB-INF\classes)
现在是想把D:\workspace\prpall\WEB-INF\classes路径下所有的文件打包成prpall.jar。然后继续如下操作:
cd D: 回车
cd workspace/prpal
- [原创]JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
comsci
eclipse设计模式算法工作swing
JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
&nb
- SecureCRT右键粘贴的设置
daizj
secureCRT右键粘贴
一般都习惯鼠标右键自动粘贴的功能,对于SecureCRT6.7.5 ,这个功能也已经是默认配置了。
老版本的SecureCRT其实也有这个功能,只是不是默认设置,很多人不知道罢了。
菜单:
Options->Global Options ...->Terminal
右边有个Mouse的选项块。
Copy on Select
Paste on Right/Middle
- Linux 软链接和硬链接
dongwei_6688
linux
1.Linux链接概念Linux链接分两种,一种被称为硬链接(Hard Link),另一种被称为符号链接(Symbolic Link)。默认情况下,ln命令产生硬链接。
【硬连接】硬连接指通过索引节点来进行连接。在Linux的文件系统中,保存在磁盘分区中的文件不管是什么类型都给它分配一个编号,称为索引节点号(Inode Index)。在Linux中,多个文件名指向同一索引节点是存在的。一般这种连
- DIV底部自适应
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- Centos6.5使用yum安装mysql——快速上手必备
dcj3sjt126com
mysql
第1步、yum安装mysql
[root@stonex ~]# yum -y install mysql-server
安装结果:
Installed:
mysql-server.x86_64 0:5.1.73-3.el6_5 &nb
- 如何调试JDK源码
frank1234
jdk
相信各位小伙伴们跟我一样,想通过JDK源码来学习Java,比如collections包,java.util.concurrent包。
可惜的是sun提供的jdk并不能查看运行中的局部变量,需要重新编译一下rt.jar。
下面是编译jdk的具体步骤:
1.把C:\java\jdk1.6.0_26\sr
- Maximal Rectangle
hcx2013
max
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
public class Solution {
public int maximalRectangle(char[][] matrix)
- Spring MVC测试框架详解——服务端测试
jinnianshilongnian
spring mvc test
随着RESTful Web Service的流行,测试对外的Service是否满足期望也变的必要的。从Spring 3.2开始Spring了Spring Web测试框架,如果版本低于3.2,请使用spring-test-mvc项目(合并到spring3.2中了)。
Spring MVC测试框架提供了对服务器端和客户端(基于RestTemplate的客户端)提供了支持。
&nbs
- Linux64位操作系统(CentOS6.6)上如何编译hadoop2.4.0
liyong0802
hadoop
一、准备编译软件
1.在官网下载jdk1.7、maven3.2.1、ant1.9.4,解压设置好环境变量就可以用。
环境变量设置如下:
(1)执行vim /etc/profile
(2)在文件尾部加入:
export JAVA_HOME=/home/spark/jdk1.7
export MAVEN_HOME=/ho
- StatusBar 字体白色
pangyulei
status
[[UIApplication sharedApplication] setStatusBarStyle:UIStatusBarStyleLightContent];
/*you'll also need to set UIViewControllerBasedStatusBarAppearance to NO in the plist file if you use this method
- 如何分析Java虚拟机死锁
sesame
javathreadoracle虚拟机jdbc
英文资料:
Thread Dump and Concurrency Locks
Thread dumps are very useful for diagnosing synchronization related problems such as deadlocks on object monitors. Ctrl-\ on Solaris/Linux or Ctrl-B
- 位运算简介及实用技巧(一):基础篇
tw_wangzhengquan
位运算
http://www.matrix67.com/blog/archives/263
去年年底写的关于位运算的日志是这个Blog里少数大受欢迎的文章之一,很多人都希望我能不断完善那篇文章。后来我看到了不少其它的资料,学习到了更多关于位运算的知识,有了重新整理位运算技巧的想法。从今天起我就开始写这一系列位运算讲解文章,与其说是原来那篇文章的follow-up,不如说是一个r
- jsearch的索引文件结构
yangshangchuan
搜索引擎jsearch全文检索信息检索word分词
jsearch是一个高性能的全文检索工具包,基于倒排索引,基于java8,类似于lucene,但更轻量级。
jsearch的索引文件结构定义如下:
1、一个词的索引由=分割的三部分组成: 第一部分是词 第二部分是这个词在多少
![]() 和一副同样场景的HR RGB图像
和一副同样场景的HR RGB图像![]() 中恢复一副HR高光谱图像
中恢复一副HR高光谱图像![]() 。
。![]() 和
和![]() 分别表示Z和X的像素总数,L是Z的光谱数(L>>3)。
分别表示Z和X的像素总数,L是Z的光谱数(L>>3)。![]()
![]() 表示退化矩阵(模糊和下采样),P是一个变换矩阵将Z映射到它的RGB表达Y。因为X和Y的总测量值个数远小于未知Z的总个数,即
表示退化矩阵(模糊和下采样),P是一个变换矩阵将Z映射到它的RGB表达Y。因为X和Y的总测量值个数远小于未知Z的总个数,即![]() ,所以从X和Y中恢复Z是一个不适定(ill-posed)问题,常用利用未知Z的先验知识的正则化方法解决。
,所以从X和Y中恢复Z是一个不适定(ill-posed)问题,常用利用未知Z的先验知识的正则化方法解决。![]() 可以表示为少数不同的谱间特征的线性组合:
可以表示为少数不同的谱间特征的线性组合:![]()
![]() 是谱间字典,
是谱间字典,![]() 是稀疏的the fractional abundance vector ,
是稀疏的the fractional abundance vector ,![]() 是估计误差。D的每一列表示该场景覆盖物质的辐射向量。
是估计误差。D的每一列表示该场景覆盖物质的辐射向量。![]() ,所以X中的每个像素
,所以X中的每个像素![]() 可表示为:
可表示为:![]() 代表位置i处的窗
代表位置i处的窗![]() 的加权系数,
的加权系数,![]() 是一个稀疏向量。
是一个稀疏向量。![]()
![]() 可以从Y中估计得到。
可以从Y中估计得到。![]()
![]() ,但是,式(5)中谱间字典D和系数矩阵A都未知。本文打算利用X和Y来估计D和A。
,但是,式(5)中谱间字典D和系数矩阵A都未知。本文打算利用X和Y来估计D和A。![]() 是系数矩阵,V是估计误差矩阵,假设为加性高斯噪声。B和D都未知。
是系数矩阵,V是估计误差矩阵,假设为加性高斯噪声。B和D都未知。![]() 是拉格朗日乘子
是拉格朗日乘子![]() 。
。![]() ,S,B更新方式分别为:
,S,B更新方式分别为:![]() 是软收缩算子,并且
是软收缩算子,并且![]()
![]() 表示第t次迭代后的字典,
表示第t次迭代后的字典,![]()
![]() 则
则![]() 可以通过求解式(15)得到:
可以通过求解式(15)得到: