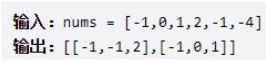【数据结构与算法】第三篇：题型积累

系列文章目录

提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
TODO:写完再整理

---

前言

认知有限，望大家多多包涵，有什么问题也希望能够与大家多交流，共同成长！

本文先对数据结构与算法–简单题型做个简单的介绍，具体内容后续再更，其他模块可以参考去我其他文章

---

提示：以下是本篇文章正文内容

一、刷题的准备与步骤

（1）第一步：先学会至少一种计算机语言、学习数据结构和算法的知识框架

【理解算法的核心思想】

.

（2）第二步：【重点】根据步骤模板刷题，分类总结写感想

【做题量的积累】

（1）题目理解（理解能力）

（1）输入
（2）输出
（3）限制条件

注意
（1）【审题能力很重要】题目把计算机知识和真实情况建立了桥梁，进行了比喻，自己要看穿复现回来

（2）要坚持但不要太执着，审完题，如果没有算法思路，这道题肯定是做不出来的，赶紧跳到下一题，把会做的先做了，不会做的提供审题和算法思路结果就好，但是整体不能放弃，把笔试时间用完（态度）！

.

（2）解题思路（找规律）（理论知识储备和逻辑能力）

（1）画图（示例）找规律，理清解题思路
（2）匹配数据结构与算法工具

注意
（1）一道题目是由多个知识点组成的，建立知识点的逻辑关系

（2）放开格局去思考问题，不一定要用最优的方式进行解题，至少有一种可实现的解题思路即可（暴力求解的方法也好）

【刷题心得】复杂的算法都是可以简单实现的
1）暴力求解实现

不论是数据结构还是算法，掌握基础的实现是最重要的！
即数据结构掌握简单的数据结构，算法掌握常用的算法思想【掌握基础的数据结构与算法就能偶使用暴力求解】

能找到一种方法简单有效实现就行，未排序之前一般使用的是暴力的算法，排序后一般使用有技巧的方法；
变量数组的方式一般是解决简单问题，列表哈希表树图这种数据结构是解决巧妙的问题

能用简单有效的数据结构尽量简单实现，毕竟能做出来有个结果先，优化是第二步考虑的

2）其他算法实现

（1）通过数据结构能不能解决
（2）通过算法能不能解决
（3）思考问题的方向：正向思考，反向思考，中间分开思考

.

（3）代码实现（工程代码实现及debug能力）

（1）思考算法有没有提供的是什么通用模板
（2）对照示例和图，根据思路去编程，然后debug和纠错迭代

注意
（1）编写程序函数不要太大，子功能实现过程太大的时候可以分子函数编写，这样思路更清晰。一些固定功能可以包装成子函数

（2）编程算法更多考虑的是知识点怎么通过逻辑嵌入到思路中

（4）思想感悟及积累

.

（3）第三步：背题、多练习加深印象

【举一反三做部署】
.

（4）第四步：不能急于求成，肯花时间，踏出第一步，不要局限在自己现在的水平

.
.

二、数据结构相关题型积累

（0）变量运算

12. 整数转罗马数字【字符串、变量的转换】

（1）题目
整数转罗马数字
.

（2）审题
输入:整数
输出:罗马数字
限制条件:

.
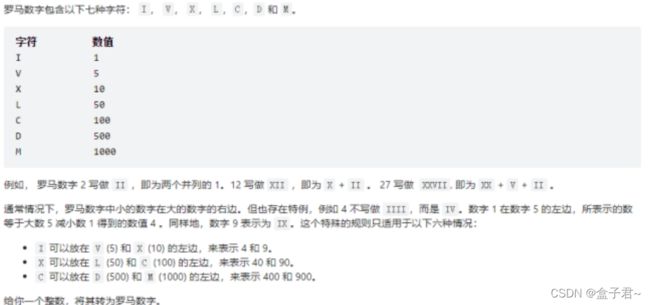
（3）解题思路
图例

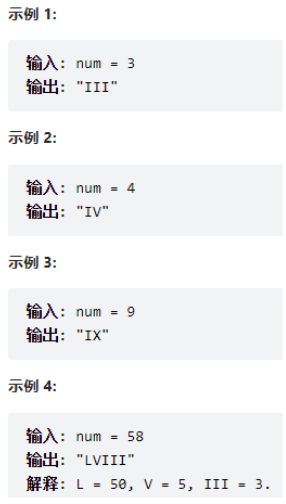
整体解题步骤

（1）把罗马数字对应的表示用一个静态数组表示
（2）遍历所有的静态数组中的整数
（3）当num大于静态数组中的某一个元素的时候，就相减，直到num为0

（4）编程实现

const pair<int, string> valueSymbols[] = {//把罗马数字对应的表示用一个静态数组表示
    {1000, "M"},
    {900,  "CM"},
    {500,  "D"},
    {400,  "CD"},
    {100,  "C"},
    {90,   "XC"},
    {50,   "L"},
    {40,   "XL"},
    {10,   "X"},
    {9,    "IX"},
    {5,    "V"},
    {4,    "IV"},
    {1,    "I"},
};

class Solution {
public:
    string intToRoman(int num) {
        string roman;       //定义罗马字符串
        for (const auto &[value, symbol] : valueSymbols) {//遍历所有的静态数组中的整数
            while (num >= value) {//当num大于静态数组中的某一个元素的时候，就相减，直到num为0
                num -= value;
                roman += symbol;
            }
            if (num == 0) {
                break;
            }
        }
        return roman;
    }
};

.

8. 字符串转换整数 (atoi)

（1）题目

（2）解题思路

1）字符串滤除空格的方法

2）字符串判断正负号的方法

3）字符串转整数的方法（注意溢出）

（3）编程实现

.
.

---

（1）数组（矩阵）【暴力、查找、合并、排序，双指针，哈希表】

34. 在排序数组中查找元素的第一个和最后一个位置

（1）题目

给定一个按照升序排列的整数数组 nums，和一个目标值 target。
找出给定目标值在数组中的开始位置和结束位置。

（2）审题

输入：给定一个按照升序排列的整数数组 nums，和一个目标值 target。

输出：找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]

（3）解题思路

	1）图例
		示例 1：
		输入：nums = [5,7,7,8,8,10], target = 8
		输出：[3,4]
		
		示例 2：
		输入：nums = [5,7,7,8,8,10], target = 6
		输出：[-1,-1]
		
		示例 3：
		输入：nums = [], target = 0
		输出：[-1,-1]
	
	2）数据结构与算法匹配
		数据结构：数组
		算法：二分查找

（3）整体解题步骤
1）暴力的解法
	（1）计算数组长度
	（2）正向for循环遍历数组，找到与目标值target相同元素的下标，若没有与target值相同的的下标，则返回[-1,-1]
	（3）逆向for循环遍历数组，找到与目标值target相同元素的下标
	（4）返回两个下标[i,j]

（2）二分查找

（4）编程实现
二分查找

class Solution { 
public:
    int binarySearch(vector<int>& nums, int target, bool lower) {//二分查找
        int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();
        while (left <= right) {
            int mid = (left + right) / 2;//计算中间的下标
            if (nums[mid] > target || (lower && nums[mid] >= target)) {//左区间搜索
                right = mid - 1;
                ans = mid;
            } else {            //右区间搜索
                left = mid + 1;
            }
        }
        return ans;
    }

    vector<int> searchRange(vector<int>& nums, int target) {
        int leftIdx = binarySearch(nums, target, true);//寻找左下标值
        int rightIdx = binarySearch(nums, target, false) - 1;//寻找右下标值
        if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {//存在元素的情况
            return vector<int>{leftIdx, rightIdx};
        } 
        return vector<int>{-1, -1};
    }
};

.
.

163. 缺失的区间

（1）题目理解

	（1）输入
		（1）一个已经排了序的整形数组
		（2）一个给定上下限的闭区间范围
	
	（2）输出
		（1）输出缺失的整数区间（注意格式）
	
	（3）限制
		无

（2）解题思路

示例
	输入: nums = [0, 1, 3, 50, 75], lower = 0 和 upper = 99,
	输出: ["2", "4->49", "51->74", "76->99"]

思路
	（1）先通过数组查找，找到下限lower与上限upper在数组内插入的对应下标
	（2）把lower、区间内的数组元素、upper三者组成一个新的数组
	（3）判断新数组的长度length
	（4）【三种情况】根据（length-1）的次数，正序两两元素做差，
		若差值为1就跳过
		若差值为2就输出(nums[i]+1)到字符串res
		若差值大于2就输出(nums[i]+1 -> nums[i+1]-1)到字符串res

数据结构与算法工具

1）数据结构
（1）vector数据结构增加一个元素
	vector res;
	res.push_back（）

2）算法
	数组查找的方法

（3）代码实现
（这个代码是暴力一个一个区间寻找，没有用做差的方式）

class Solution {
public:
    vector<string> findMissingRanges(vector<int>& nums, int lower, int upper) 
    {
        vector<string> res;
        int pre=lower-1;
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]==pre+2)res.push_back(to_string(pre+1));
            else if(nums[i]>pre+2)res.push_back(to_string(pre+1)+"->"+to_string(nums[i]-1));
            pre=nums[i];
        }
        if(upper==pre+1)res.push_back(to_string(pre+1));
        else if(upper-pre>1)res.push_back(to_string(pre+1)+"->"+to_string(upper));
        return res;
    }
};

（4）思想感悟

解题思路就是判断数组是否连续，既可以用做差的方式判断，也可以用动态变量pre的方式判断元素是否相等判断

.
.

88. 合并两个有序数组【基础】

（1）题目理解

（1）输入
	（1）两个数组nums1，nums2
	（2）该两个数组的长度m和n（其实可以不要，降低难度而已）

（2）输出
	（1）合并两个数组并按升序进行排序

（3）限制条件
	无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	【示例】
	输入：nums1 = [1,2,3], m = 3, nums2 = [2,5,6], n = 3
	输出：[1,2,2,3,5,6]
	
	【思路】
	（1）根据两个数组长度，手动合并两个数组
	（2）对两个数组进行排序，并输出新的数组

（2）匹配数据结构与算法工具
	数组的数据类型操作及排序

（3）代码实现

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        for (int i = 0; i != n; ++i) {//数组合并
            nums1[m + i] = nums2[i];
        }
        sort(nums1.begin(), nums1.end());//数组排序
    }
};

.

66.加一【逻辑推理】

（1）题目理解

（1）输入
	（1）一个非负的整数数组	

（2）输出
	（1）把该整数数组的最后一个元素加一并输出

（3）限制条件
	无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	输入：digits = [1,2,3]
	输出：[1,2,4]
	
	思路
	当我们对数组 digits 加一时，我们只需要关注 digits 的末尾出现了多少个9 即可。我们可以考虑如下的三种情况：
	
	如果 digits 的末尾没有 9，例如 [1,2,3]，那么我们直接将末尾的数加一，得到[1,2,4] 并返回；
	
	如果digits 的末尾有若干个 9，例如 [1,2,3,9,9]，那么我们只需要找出从末尾开始的第一个不为 9 的元素，即 3，将该元素加一，得到[1,2,4,9,9]。随后将末尾的 99 全部置零，得到 [1,2,4,0,0] 并返回。
	
	如果 digits 的所有元素都是 99，例如 [9,9,9,9,9]，那么答案为 [1,0,0,0,0,0]。我们只需要构造一个长度比 \textit{digits}digits 多 11 的新数组，将首元素置为 11，其余元素置为 00 即可。
	
	算法
	只需要对数组 digits 进行一次逆序遍历，找出第一个不为 9 的元素，将其加一并将后续所有元素置零即可。如果 digits 中所有的元素均为 9，那么对应着「思路」部分的第三种情况，我们需要返回一个新的数组。



（2）匹配数据结构与算法工具
	（1）数据结构：数组下表取元素操作，变量运算
	（2）算法
		逆序数组暴力查找、数学逻辑推理

（3）代码实现

class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int n = digits.size();            //获取数组长度
        for (int i = n - 1; i >= 0; --i) {//逆序遍历
            if (digits[i] != 9) {         //找到不为9的元素
                ++digits[i];              //元素值加一
                for (int j = i + 1; j < n; ++j) {//后面置0
                    digits[j] = 0;
                }
                return digits;
            }
        }
        // digits 中所有的元素均为 9（能走到这里因为没有return出去）
        vector<int> ans(n + 1);
        ans[0] = 1;
        return ans;
    }
};

.
.

121. 买卖股票的最佳时机

（1）题目理解

（1）输入
	（1）一个无序的整数数组

（2）输出
	（1）该无序数组中，逆序某两个元素之差的最大值

（3）限制条件
	差值不能是负数（差值为负数的时候不会买入的）

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	输入：[7,1,5,3,6,4]
	输出：5

（2）思路：暴力求解
	从后往前一次遍历所有的两两元素，进行判断记录
	（1）先计算数组的长度length
	（2）设计两个for循环嵌套一次遍历任意两个元素
	（3）判断若后一个元素与前一个元素之差大于0，则把该差值与res比较，取最大值
	（4）返回最大的差值res

（3）匹配数据结构与算法工具
	1）数据结构：数组、整数变量取最大值、最小值max(A,B)、min(a,b)

	2）算法
	（1）暴力求解
	（2）双指针

（3）代码实现
这种方法没有使用逆序，但是依然实现了后一个元素-前一个元素

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = (int)prices.size(), ans = 0;
        for (int i = 0; i < n; ++i){
            for (int j = i + 1; j < n; ++j) {
                ans = max(ans, prices[j] - prices[i]);
            }
        }
        return ans;
    }
};

11. 盛最多水的容器【数组暴力遍历】

（1）题目
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
.
（2）审题

输入：给定一个长度为 n 的整数数组 height
输出：找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水
限制条件：你不能倾斜容器

.
（3）解题思路
图例

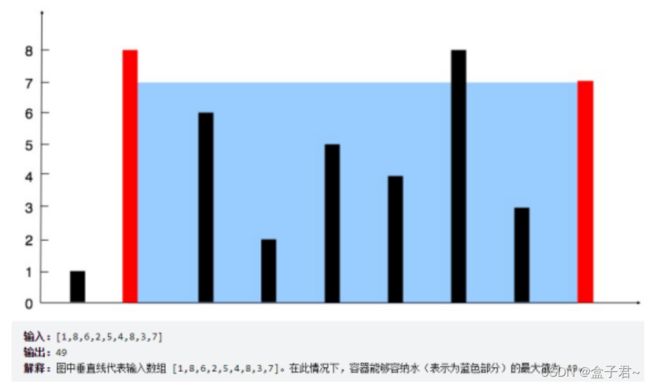
整体解题步骤
方法一：暴力两个for循环
（1）两两for循环遍历全部数组
（2）水量的计算=两元素取最小值*两元素下标差
（3）max当前最大的水量，循环结束，输出水量

方法二：双指针

编程实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l = 0, r = height.size() - 1;
        int ans = 0;
        while (l < r) {
            int area = min(height[l], height[r]) * (r - l);
            ans = max(ans, area);
            if (height[l] <= height[r]) {
                ++l;
            }
            else {
                --r;
            }
        }
        return ans;
    }
};

15. 三数之和【数组】

（1）题目
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

.
（2）审题

输入：一个包含 n 个整数的数组 nums
输出：a + b + c = 0 且不重复的三元组
限制条件：无

.
（3）解题思路

图例

整体解题步骤
三重for循环
.
（4）编程实现

for(int i=0;i<len;i++)
for(int j=i+1;j<len;j++)
for(int k=j+1;k<len;k++)

.

16. 最接近的三数之和

（1）题目

给你一个长度为 n 的整数数组 nums 和 一个目标值 target。
请你从 nums 中选出三个整数，使它们的和与 target 最接近。返回这三个数的和。

（2）审题

输入：一个长度为 n 的整数数组 nums 和 一个目标值 target

输出：从 nums 中选出三个整数，使它们的和与 target 最接近的返回这三个数的和

限制条件：假定每组输入只存在恰好一个解

（3）解题思路

（1）图例
	示例 1：
	输入：nums = [-1,2,1,-4], target = 1
	输出：2
	解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 
	
	示例 2：
	输入：nums = [0,0,0], target = 1
	输出：0


（2）数据结构与算法匹配
	数据结构：数组
	算法：双指针

（3）整体解题步骤
（1）暴力解法
		题目要求找到与目标值 target 最接近的三元组，这里的「最接近」即为差值的绝对值最小。
		我们可以考虑直接使用三重循环枚举三元组，找出与目标值最接近的作为答案
		（1）三重for循环遍历整个数组
		（2）求解三个元素之和，并与target取最小值
		（3）不断取绝对值的最小值，直到遍历完成数组

（2）排序+双指针【这个复杂一点】

（4）编程实现

排序+双指针实现方法

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        int best = 1e7;

        // 根据差值的绝对值来更新答案
        auto update = [&](int cur) {
            if (abs(cur - target) < abs(best - target)) {
                best = cur;
            }
        };

        // 枚举 a
        for (int i = 0; i < n; ++i) {
            // 保证和上一次枚举的元素不相等
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 使用双指针枚举 b 和 c
            int j = i + 1, k = n - 1;
            while (j < k) {
                int sum = nums[i] + nums[j] + nums[k];
                // 如果和为 target 直接返回答案
                if (sum == target) {
                    return target;
                }
                update(sum);
                if (sum > target) {
                    // 如果和大于 target，移动 c 对应的指针
                    int k0 = k - 1;
                    // 移动到下一个不相等的元素
                    while (j < k0 && nums[k0] == nums[k]) {
                        --k0;
                    }
                    k = k0;
                } else {
                    // 如果和小于 target，移动 b 对应的指针
                    int j0 = j + 1;
                    // 移动到下一个不相等的元素
                    while (j0 < k && nums[j0] == nums[j]) {
                        ++j0;
                    }
                    j = j0;
                }
            }
        }
        return best;
    }
};

.
.

118. 杨辉三角【动态数组vector】

（1）题目
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

（2）审题

输入:给定一个非负整数 numRows
输出:「杨辉三角」的前 numRows 行
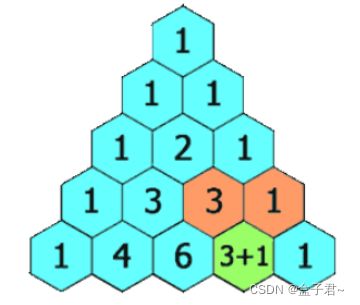
限制条件:在「杨辉三角」中，每个数是它左上方和右上方的数的和。

（3）解题思路
图例

整体解题步骤

（1）先生成 numRows行的vector向量
（2）再对每一行向量的元素进行resize()
（3）把每一行的向量首位两个元素置为1
（4）利用杨辉三角计算生成下一行的元素（使用两个for循环）

（4）编程实现

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> ret(numRows);//创建杨辉三角的每一行的元素
        for (int i = 0; i < numRows; ++i) {
            ret[i].resize(i + 1);         //每一行的元素个数加一个
            ret[i][0] = ret[i][i] = 1;    //每一行的第一个和最后一个元素为1
            for (int j = 1; j < i; ++j) {//两数之和填充杨辉三角
                ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
            }
        }
        return ret;
    }
};

6. Z 字形变换

（1）题目

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

（2）审题

输入：给定字符串 s

输出：从左到右进行 Z 字形排列。

（3）解题思路

1）图例

2）数据结构与算法匹配

数据结构：数组、矩阵
算法：数学

3）整体解题步骤

（0）如果原字符串只有一行或者一列，直接输出
（1）先通过Z型变换计算二维矩阵的列数n，行数m题目已经给定了
（2）创建一个m*n的矩阵，计算Z变换的每一个周期（数学关系），按照行数填充垂直列元素，按照列数填充斜向上的行元素，直到遍历完字符串的长度
（3）将二维矩阵的元素排列成字符串

（4）编程实现

class Solution {
public:
    string convert(string s, int numRows) {
        int n = s.length(), r = numRows;//如果原字符串只有一行或者一列，直接输出
        if (r == 1 || r >= n) {
            return s;
        }
        int t = r * 2 - 2;//计算Z变换的每一个周期（数学关系）
        int c = (n + t - 1) / t * (r - 1);//计算二维矩阵的列数（数学关系）
        vector<string> mat(r, string(c, 0));//创建一个m*n的矩阵
        for (int i = 0, x = 0, y = 0; i < n; ++i) {
            mat[x][y] = s[i];   //矩阵填充
            if (i % t < r - 1) {// 向下移动
                ++x; 
            } else {// 向右上移动
                --x;
                ++y; 
            }
        }
        string ans;
        for (auto &row : mat) {//将二维矩阵的元素排列成字符串
            for (char ch : row) {
                if (ch) {
                    ans += ch;
                }
            }
        }
        return ans;
    }
};

（5）积累

1）创建一个n*m的矩阵

vector<string> mat(n,m);
vector<int> mat(n,m);

2）矩阵的填充

mat[x][y] = s[i];   //矩阵填充

3）将二维矩阵的元素排列成字符串

string ans;
        for (auto &row : mat) {//将二维矩阵的元素排列成字符串
            for (char ch : row) {
                if (ch) {
                    ans += ch;
                }
            }
        }
        return ans;

36. 有效的数独（矩阵）

（1）题目

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

（2）审题

输入：一个 9 x 9 的矩阵
输出：一个bool的数据，若是有效数独，输出true，反之输出false
限制条件：无

（3）解题思路

1）图例

2）数据结构与算法匹配
	数据结构：矩阵（二维数组）
	算法：暴力遍历

3）整体解题步骤
	（1）遍历一个二维数组（矩阵）
	（2）遍历的时候取出矩阵中的元素，分别判断该元素在所在行、列、九宫格内是否重复出现

（4）编程实现

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        //暴力遍历整个二维数组（矩阵）
        for(int i = 0; i < board.size(); i++){//行的长度
            for(int j = 0; j < board[0].size(); j++){//列的长度
                if(board[i][j] >= '0' && board[i][j] <= '9'){//元素在1~9之间
                    if(!getEffective(i, j, board)){
                        return false;
                    }
                }
            }
        }
        return true;

    }

 //判断是否为有效字符--即判断该board[i][j]是否在之前已经存在过
    bool getEffective(int i, int j, vector<vector<char>>& board){
        // 验证一行
        for(int k = 0; k < board[i].size(); k++){
            if(board[i][k] == board[i][j] && k != j){//元素相同
                return false;
            }
        }
        // 验证一列
        for(int k = 0; k < board.size(); k++){
            if(board[k][j] == board[i][j] && k != i){//元素相同
                return false;
            }
        }
        // 验证当前 3 * 3 数组
        int heng = (i / 3) * 3;//分离出当前九宫格的行起点
        int zhong = (j / 3) * 3;//分离出当前九宫格的列起点

        for(int k1 = heng; k1 < heng + 3; k1++){
            for(int k2 = zhong; k2 < zhong + 3; k2++){
                if((board[k1][k2] == board[i][j]) && (k1 != i && k2 != j)){//元素相同
                    return false;
                }
            }
        }

        return true;
    }


};

（5）积累

（1）矩阵可以理解成为一个二维数组
（2）遍历一个矩阵的方法

.
.

---

（2）字符串

157. 用 Read4 读取 N 个字符

（1）题目理解

（1）输入
	一个字符文件

（2）输出
	读取文件读取的字符串为n个，并返回字符读取的真实数量

（3）限制
	该文件只能通过提供的 read4（）API 方法来读取

	read4方法相关（提供的）
		
		1、read4方法的功能
			API read4 可以从文件中读取 4 个连续的字符，并且将它们写入缓存数组 buf 中。
			
			返回值为实际读取的字符个数。
			
			注意 read4() 自身拥有文件指针，很类似于 C 语言中的 FILE *fp 。
		
		2、read4方法的定义
			参数类型: char[] buf4
			返回类型: int
			
			注意: buf4[] 是目标缓存区不是源缓存区，read4 的返回结果将会复制到 buf4[] 当中。
		
		3、read4方法的调用例子
			File file("abcde"); // 文件名为 "abcde"， 初始文件指针 (fp) 指向 'a' 
			char[] buf4 = new char[4]; // 创建一个缓存区使其能容纳足够的字符
			read4(buf4); // read4 返回 4。现在 buf4 = "abcd"，fp 指向 'e'
			read4(buf4); // read4 返回 1。现在 buf4 = "e"，fp 指向文件末尾
			read4(buf4); // read4 返回 0。现在 buf = ""，fp 指向文件末尾
			
			示例 1
			输入： file = "abc", n = 4
			输出： 3
			解释： 当执行你的 read 方法后，buf 需要包含 "abc"。 文件一共 3 个字符，因此返回 3。 注意 "abc" 是文件的内容，不是 buf 的内容，buf 是你需要写入结果的目标缓存区。
			
			
			示例 2
			输入： file = "abcde", n = 5
			输出： 5
			解释： 当执行你的 read 方法后，buf 需要包含 "abcde"。文件共 5 个字符，因此返回 5。
			
			
			示例 3
			输入： file = "abcdABCD1234", n = 12
			输出： 12
			解释： 当执行你的 read 方法后，buf 需要包含 "abcdABCD1234"。文件一共 12 个字符，因此返回 12。
		
		提示
		你 不能 直接操作该文件，文件只能通过 read4 获取而 不能 通过 read的官方方法。
		read  函数只在每个测试用例调用一次。
		你可以假定目标缓存数组 buf 保证有足够的空间存下 n 个字符

（2）解题思路

输入一个文件的所有内容，迭代地4个字符4个字符的依次读取，每次读取记录相关的内容和字符数目

（3）代码实现

class Solution1 {
public:
    /**
     * @param buf Destination buffer
     * @param n   Number of characters to read
     * @return    The number of actual characters read
     */
    int read(char *buf, int n) {
        int res = 0;//定义字符数量的中间变量
        for (int i = 0; i < n; i += 4) {//每4个字符取一次
            int count = read4(buf + i);
            res += min(count, n - i);
        }    

        return res;    
    }
};

（4）思想感悟
1）读文件之前先要打开文件（变成语言实现的），在通过read的内置方法实现

.

14. 最长公共前缀

（1）题目理解

（1）输入
	（1）一个字符串数组

（2）输出
	（1）若不存在公共前缀，输出一个空字符
	（2）若存在公共前缀，则输出最大公共前缀公共

（3）限制
	无

（2）解题思路

（1）横向扫描的方法【比较好】

依次遍历字符串数组中的每个字符串，对于每个遍历到的字符串，更新最长公共前缀，当遍历完所有的字符串以后，即可得到字符串数组中的最长公共前缀。
如果在尚未遍历完所有的字符串时，最长公共前缀已经是空串，则最长公共前缀一定是空串，因此不需要继续遍历剩下的字符串，直接返回空串即可。

.
（2）纵向扫描的方法【比较好】

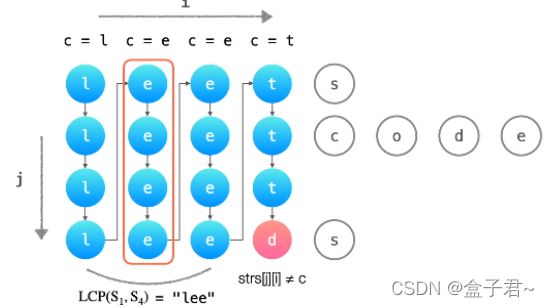
纵向扫描时，从前往后遍历所有字符串的每一列，比较相同列上的字符是否相同，如果相同则继续对下一列进行比较，如果不相同则当前列不再属于公共前缀，当前列之前的部分为最长公共前缀。

（1）先遍历取出所有字符串元素，确定最小字符串元素的size
（2）【两个for循环嵌套】运行sizr次for循环，每次循环判断对应列的元素是否一致，若一致就继续运行循环，若不一致就退出循环，根据最长公共前缀的index，返回最长公共前缀

.
（3）分治的方法（分治有模板）

在上面两中方法的基础上，对复杂度进行优化的方法，先把一整个字符串划分为两个（多个）子字符串，根据横纵两种方法对两个子字符串进行取公共前缀，两个公共前缀在用同样的方法进行取公共前缀

.
（4）二分查找法（二分查找有模板）

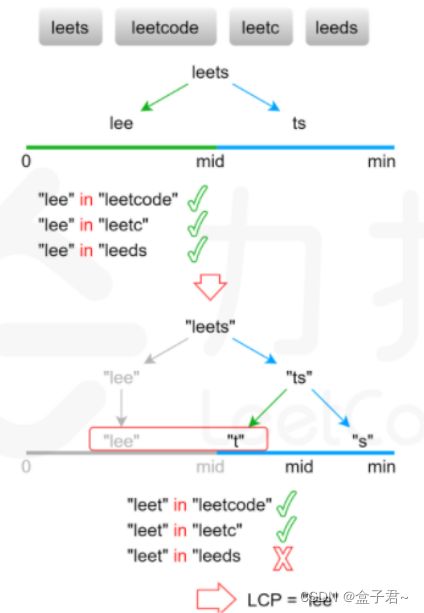
最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。用 minLength 表示字符串数组中的最短字符串的长度，则可以在[0,minLength] 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 mid，判断每个字符串的长度为 mid 的前缀是否相同，如果相同则最长公共前缀的长度一定大于或等于 mid，如果不相同则最长公共前缀的长度一定小于 \textit{mid}mid，通过上述方式将查找范围缩小一半，直到得到最长公共前缀的长度

（3）代码实现

（1）横向扫描的方法

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {//如果输入的字符串是空的，则直接返回空字符串
            return "";
        }
        string prefix = strs[0];             //若字符串非空，使用字符串的第一个字符元素定义公共前缀
        int count = strs.size();             //获取字符串长度
        for (int i = 1; i < count; ++i) {//遍历字符串所有的字符元素
            prefix = longestCommonPrefix(prefix, strs[i]);//输入一个字符元素，获取其公共前缀
            if (!prefix.size()) {                                                    //若公共前缀为空，没必要在遍历了
                break;
            }
        }
        return prefix;
    }

    //输入一个字符元素，获取其公共前缀
    string longestCommonPrefix(const string& str1, const string& str2) {
        int length = min(str1.size(), str2.size());//取字符数量小的为长度
        int index = 0;
        while (index < length && str1[index] == str2[index]) {//遍历相同的元素，获取公共字符串的长度
            ++index;
        }
        return str1.substr(0, index);
    }
};

（2）纵向扫描的方法

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {//若输入的字符串为空，则输出空字符串
            return "";
        }
        int length = strs[0].length();     //在这里取第一个字符穿元素的长度为遍历次数【这样也可以，短的元素空了就停止循环了】（应该可以优化成先遍历取出所有字符串元素，确定最小字符串元素的size）
        int count = strs.length;           //计算字符串元素个数
        for (int i = 0; i < length; i++) {//遍历列字符
            char c = strs[0].charAt(i);   //取第一个元素的第i个字符
            for (int j = 1; j < count; j++) {//遍历行元素
                if (i == strs[j].length() || strs[j].charAt(i) != c) {//若前缀相同或者该行元素已经是最短了，输出公共前缀
                    return strs[0].substring(0, i);
                }
            }
        }
        return strs[0];
    }
}

（3）分治的方法

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {//若输入的字符串为空，则输出空字符串
            return "";
        }
        else {
            return longestCommonPrefix(strs, 0, strs.size() - 1);//使用分治的方法进行去公共前缀
        }
    }

    //使用分治的方法进行去公共前缀
    string longestCommonPrefix(const vector<string>& strs, int start, int end) {
        if (start == end) {//若只有一个元素
            return strs[start];
        }
        else {
            int mid = (start + end) / 2;
            string lcpLeft = longestCommonPrefix(strs, start, mid);       //递归调用自己
            string lcpRight = longestCommonPrefix(strs, mid + 1, end);//递归调用自己
            return commonPrefix(lcpLeft, lcpRight);//把最终两部分求公共前缀
        }
    }

    string commonPrefix(const string& lcpLeft, const string& lcpRight) {
        int minLength = min(lcpLeft.size(), lcpRight.size());
        for (int i = 0; i < minLength; ++i) {
            if (lcpLeft[i] != lcpRight[i]) {
                return lcpLeft.substr(0, i);
            }
        }
        return lcpLeft.substr(0, minLength);
    }
};

（4）二分查找法

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        int minLength = Integer.MAX_VALUE;
        for (String str : strs) {
            minLength = Math.min(minLength, str.length());
        }
        int low = 0, high = minLength;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return strs[0].substring(0, low);
    }

    public boolean isCommonPrefix(String[] strs, int length) {
        String str0 = strs[0].substring(0, length);
        int count = strs.length;
        for (int i = 1; i < count; i++) {
            String str = strs[i];
            for (int j = 0; j < length; j++) {
                if (str0.charAt(j) != str.charAt(j)) {
                    return false;
                }
            }
        }
        return true;
    }

（4）思想感悟及积累

（1）分治发和二分查找的方法是有模板思想可以套用的

（2）编写程序函数不要太大，实现过程太大的时候可以分子函数编写

（3）字符串也可以指定取其中的某几个字符的


（4）字符串可以取其中的某一个特定下标的元素


（5）判断字符串和数组的元素长度用length

.
.

3. 无重复字符的最长子串【滑动窗口】

（1）题目理解

	（1）输入
		（1）一个字符串，如s = "abcabcbb"
	
	（2）输出
		（1）该字符串不含有重复字符的 最长子串 的长度n
	
	（3）限制条件
		无


（2）解题思路（找规律）
	（1）画图（示例）找规律并给出思路
	输入: s = "abcabcbb"
	输出: 3 
	解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
	
	输入: s = "bbbbb"
	输出: 1
	解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
	
	输入: s = "pwwkew"
	输出: 3
	解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。


1）方法1：暴力解法
	（1）计算字符串的长度len ,若字符串的长度为0，直接return 0
	（2）设计一个for循环遍历所有的字串【行列式举例】
	for( int i=2;i0;j--) //遍历次数
	（3）判断每个子字符串中是否有重复的元素【暴力两两元素遍历for循环可以，排序+双指针可以，哈希表也可以】，返回bool
	（4）若返回值为false,记录该字串长度res=i

2）方法2：滑动窗口
	（1）计算字符串的长度len ,若字符串的长度为0，直接return 0
	（2）【滑动窗口的方法】设计两个for循环依次遍历两两元素，判断两个元素是否相等，返回bool
	（3）若返回true，把两个元素的下标求差并计算绝对值，在比较最大字符串max(abs,res)
	（4）若整个循环都完成了，res还是为0，则return len，反之，返回res

（2）匹配数据结构与算法工具

1）数据结构
		字符串

2）算法
	暴力for循环、滑动窗口

（3）代码实现

（1）方法1：暴力解法
实现复杂度较高

（2）方法2：滑动窗口

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        // 哈希集合，记录每个字符是否出现过
        unordered_set<char> occ;
        int n = s.size();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        // 枚举左指针的位置，初始值隐性地表示为 -1
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.erase(s[i - 1]);
            }
            while (rk + 1 < n && !occ.count(s[rk + 1])) {
                // 不断地移动右指针
                occ.insert(s[rk + 1]);
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = max(ans, rk - i + 1);
        }
        return ans;
    }
};

（4）思想感悟及积累

字符串可以理解成为一个字符数组（若字符串的元素为字符）

【动态窗口算法的使用特征】涉及子串的问题可以用滑动窗口算法
滑动窗口的算法起始也是for循环遍历两两元素的算法，窗口的大小可以改变，只是取了一个好听一点的名字

【哈希表的使用特征】涉及出现的次数问题，可以用哈希表，数组的元素作为键，元素的下标或者出现的次数作为值

.

344. 反转字符串

（1）题目理解

（1）输入
	（1）输入一个字符串s

（2）输出
	（1）将该字符串的所有元素进行反转后，输出反转的字符串

（3）限制条件
	不分配额外的空间，在原数组中进行修改

（2）解题思路（找规律）

（1）画图（示例）找规律
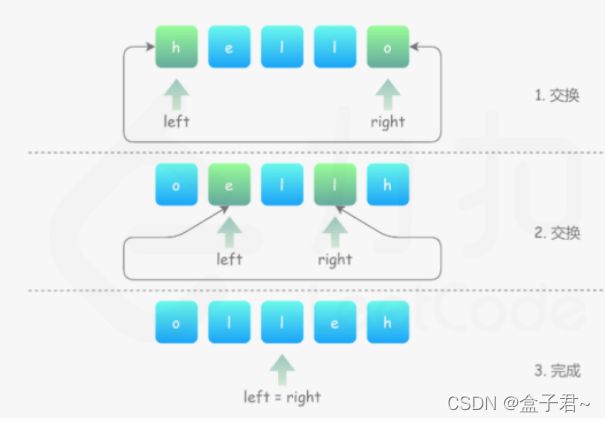
	输入：s = ["h","e","l","l","o"]
	输出：["o","l","l","e","h"]
	
	输入：s = ["H","a","n","n","a","h"]
	输出：["h","a","n","n","a","H"]

（2）思路–双指针的方法

（1）计算字符串的长度len 
（2）定义双指针，快指针fast指向字符串的头部，慢指针slow指向字符串的尾部
（3）进行（len/2）次循环，快指针fast与慢指针slow所指向的元素互换swap(a,b)，然后fast++,slow--
（4）循环结束（fast==slow），return s


（3）匹配数据结构与算法工具
	
	（1）数据结构：字符串
	（2）算法：双指针算法

（3）代码实现

class Solution {
public:
    void reverseString(vector<char>& s) {
        int n = s.size();
        for (int left = 0, right = n - 1; left < right; ++left, --right) {
            swap(s[left], s[right]);
        }
    }
};

（4）思想感悟及积累

数组与字符串对应元素交换swap(a, b);

实现 strStr() 函数【字符串】

（1）题目
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1
.
（2）审题

输入:两个字符串
输出:子字符串出现的下标，或者是-1
限制条件:无

.
（3）解题思路
图例:haystack = “hello”, needle = “ll”

整体解题步骤
我们可以让字符串 needle 与字符串haystack 的所有长度为 m 的子串均匹配一次。
为了减少不必要的匹配，我们每次匹配失败即立刻停止当前子串的匹配，对下一个子串继续匹配。如果当前子串匹配成功，我们返回当前子串的开始位置即可。如果所有子串都匹配失败，则返回 -1

.
（4）编程实现

class Solution {
public:
    int strStr(string haystack, string needle) {
        int n = haystack.size(), m = needle.size(); //获取两个字符串的长度
        for (int i = 0; i + m <= n; i++) {//当第一个字符串的元素个数大于子字符串元素个数时
            bool flag = true;
            for (int j = 0; j < m; j++) { //遍历子字符串的元素，判断有没有重叠
                if (haystack[i + j] != needle[j]) {
                    flag = false;
                    break;
                }
            }
            if (flag) {     //若发现重叠的元素，返回下标
                return i;
            }
        }
        return -1;//没有发现重叠元素
    }
};

.

---

（3）集合

217. 存在重复元素

（1）题目理解

（1）输入：一个无序数组
（2）输出：若该无序数组有重复的元素则输出ture,反之，输出false
（3）限制条件：无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路

	（1）方法一：暴力求解
		（1）计算无序数组的长度length 
		（2）设计两个for循环嵌套
		（3）在循环中，判断两两元素是否相等，若相等return true
		（3）若循环结束都没有return，则证明数组内没有重复元素返回false
	
	（2）方法二：数组排序+一维for循环
		在对数字从小到大排序之后，数组的重复元素一定出现在相邻位置中。因此，我们可以扫描已排序的数组，每次判断相邻的两个元素是否相等，如果相等则说明存在重复的元素。
		（1）计算无序数组的长度length 
		（2）对无序数组进行排序，使之成为升序数组
		（3）通过一维的for循环进行两两比较，若相等则return ture
		（4）若循环结束都没有return，则证明数组内没有重复元素返回false

	（3）方法三：数组排序+双指针
		（1）计算无序数组的长度length 
		（2）对无序数组进行排序，使之成为升序数组
		（3）定义快指针fast，慢指针slow，初始化指向数组的第一个元素
		（4）快指针fast++，并判断与慢指针slow对应的元素是否相等，若相等则return ture
		（5）若不相等则慢指针slow++
		（6）若循环结束都没有return，则证明数组内没有重复元素返回false

	（4）方法四：集合的数据结构
		对于数组中每个元素，我们将它插入到集合中。如果插入一个元素时发现该元素已经存在于集合中，则说明存在重复的元素。



（2）匹配数据结构与算法工具
	（1）数据结构：数组、集合
	
	（2）算法：数组排序、集合操作
		创建集合unordered_set s;
		查询集合s.find(x) != s.end()
		插入集合s.insert(x);

（3）代码实现
（1）方法一：暴力求解
自己实现

（2）方法二：数组排序+一维for循环

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int i = 0; i < n - 1; i++) {
            if (nums[i] == nums[i + 1]) {
                return true;
            }
        }
        return false;
    }
};

（3）方法三：数组排序+双指针
自己实现

（4）方法四：集合的数据结构

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_set<int> s;
        for (int x: nums) {
            if (s.find(x) != s.end()) {
                return true;
            }
            s.insert(x);
        }
        return false;
    }
};

（4）思想感悟及积累

（1）暴力求解是最常用的方法
（2）能用数据结构解决的问题，尽量不要用算法去解决

349. 两个数组的交集

（1）题目理解

（1）输入
	（1）两个无序且可能有重复元素的数组

（2）输出
	（1）以数组的形式输出该两个数组的交集元素

（3）限制条件
	无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	输入：nums1 = [1,2,2,1], nums2 = [2,2]
	输出：[2]
	
	输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
	输出：[9,4]

	（1）暴力求解的方法
		（1）把两个数组的重复元素去掉
		（2）计算两个数组的长度len1、len2
		（3）从任意一个数组中用for循环逐一取出元素，用另一个for循环遍历另外一个数组，判断元素是否相等
		（4）若相等，把该元素放入一个新的交集vecter数组

	（2）集合的方法【用集合的方法进行查重】
		（1）把两个数组分别赋值给两个集合
		（2）判断两个集合各自的元素个数，排在形参第一个的集合元素较少，优化复杂度【利用递归的方法】
		（3）把元素较小集合1的元素逐个判断是否在集合2中，若在则把该元素推入交集数组

（2）匹配数据结构与算法工具
	（1）数据结构：数组、集合
	
	（2）算法：数组查询、集合
		集合定义unordered_set set1
		集合插入元素set1.insert(num);
		集合元素个数查询set1.size()
		集合查询有无重复元素set2.count(num)

（3）代码实现

（1）暴力求解：自己实现

（2）集合的方法

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> set1, set2;//定义两个集合
        for (auto& num : nums1) {//把第一个数组赋值给第一个集合
            set1.insert(num);
        }
        for (auto& num : nums2) {//把第二个数组赋值给第二个集合
            set2.insert(num);
        }
        return getIntersection(set1, set2);//输入两个集合，计算交集
    }

    vector<int> getIntersection(unordered_set<int>& set1, unordered_set<int>& set2) {
        if (set1.size() > set2.size()) {//判断两个集合各自的元素个数，排在形参第一个的集合元素较少，优化复杂度【利用递归的方法】
            return getIntersection(set2, set1);
        }
        vector<int> intersection;//定义交集数组
        for (auto& num : set1) {//把元素较小集合1的元素逐个判断是否在集合2中，若在则把该元素推入交集数组
            if (set2.count(num)) {
                intersection.push_back(num);
            }
        }
        return intersection;//返回交集数组
    }
};

.

---

（4）哈希表

1. 两数之和

（1）题目理解

（1）输入
	（1）一个整型数组num
	（2）一个求和的目标值target

（2）输出
	（1）该数组中和为target值的两个元素下标

（3）限制
	同一个元素不能出现两次，答案一定存在

（2）解题思路

（1）暴力解法【for循环嵌套的巧妙建立】

暴力解法：
通过两个迭代的for循环枚举一维数组的全部元素
正解：寻找是否存在两个元素之和为target；
反解：寻找是否存在一个元素等于target-a
若存在，返回两个下标，若不存在，继续搜索

（2）哈希表查找的解法

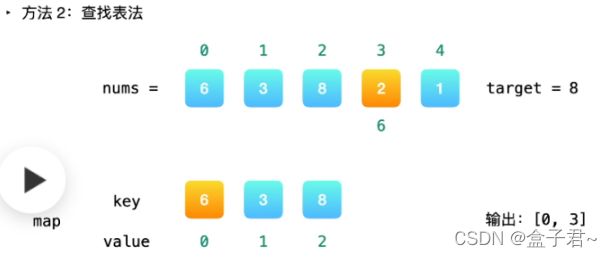
查表解法（哈希表）：
（1）初始化一个哈希表（定义键为元素的数值，值为数组元素的下标）
（2）一边建立哈希表，一边进行查询求解，使用反解的方式，先判断target-a的结果是否在哈希表中出现，若出现则直接返回下标，若没有出现则继续添加哈希表

（3）代码实现
（1）暴力解法

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return new int[]{i, j};
                }
            }
        }
        return new int[0];
    }
}

（2）哈希表查找

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashtable;//定义一个哈希表
        for (int i = 0; i < nums.size(); ++i) {  //遍历数组中所有的元素，把数组所有的元素慢慢添加到哈希表中
            auto it = hashtable.find(target - nums[i]);  //【通过输入值来查找键】判断target-a的结果是否在哈希表中出现，it是对应哈希表元素的下标
            if (it != hashtable.end()) {  //哈希表最后元素的下表是0 ，若it不是0则证明找到了
                return {it->second, i};
            }
            hashtable[nums[i]] = i;
        }
        return {};
    }
};

（4）思想感悟及积累

（0）能用和数据结构解决的问题就最好不用算法解决

（1）检查vecter数据结构的长度使用size()，检查数组array的数据结构的长度用.length

（2）哈希表的查询【通过输入值来查找键，反之也一样】
 auto it = hashtable.find(target - nums[i]);  //【通过输入值来查找键】判断target-a的结果是否在哈希表中出现，it是对应哈希表元素的下标
 
（3）哈希表的插入
hashtable[nums[i]] = i;

（4）哈希表的定义
unordered_map hashtable;

.
.

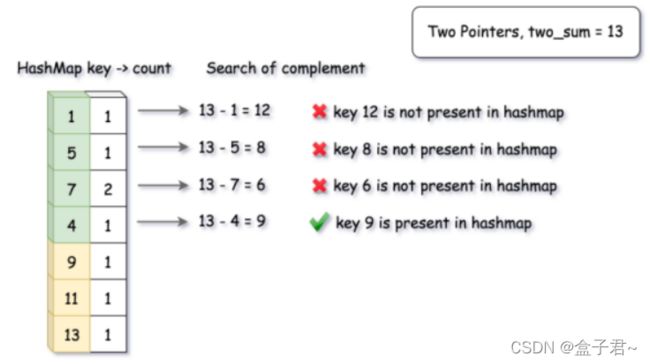
170. 两数之和 III

（1）题目理解

（1）输入
	（1）一个整数数据流
	（2）一个求和的特定值

（2）输出
	若该整数数据流中有两个元素之和等于该特定值，则输出ture，反之，输出flase

（3）限制
	无

（2）解题思路

【键是数组元素，值是出现的次数】
（1）创建一个哈希表的结构
（2）在add()中，把整数数据流中的元素添加到哈希表中的键中，把该元素出现的次数存在哈希表的值中
（3）在find()中，运行自己想的算法，给定一个求和目标值S，对于整数a,我们仅仅需要验证哈希表中的键是否存在S-a即可，前提是S-a若等于a还要满足a对应的值大于2（出现的次数大于2）

（3）代码实现–哈希表解法

class TwoSum {
public:
    unordered_map<long,long>ump;
    TwoSum() {

    }
    
    void add(int number) {
        ump[number]++;
        return ;
    }
    
    bool find(int value) {
        for(auto ite:ump){
            ump[ite.first]--;
            if(ump.count(value-ite.first)!=0&&ump[value-ite.first]>0){
                ump[ite.first]++;
                return true;
            }
            ump[ite.first]++;
        }
        return false;
    }
};

（4）思想感悟及积累

解题思路运用了哈希表中的键值对通过映射快速查询的特点，避免了数组的多次求和运算

.
.

219. 存在重复元素 II

（1）题目理解

（1）输入
	（1）一个整数无序数组
	（2）一个特定值k

（2）输出
	（1）若存在两个相同的元素，且这两个相同的元素的两下标之差小于特定值k，则返回ture

（3）限制条件
	无

（2）解题思路（找规律）

	（1）画图（示例）找规律并给出思路
		输入: nums = [1,2,3,1], k = 3
		输出: true
		
		输入: nums = [1,0,1,1], k = 1
		输出: true
		
		输入: nums = [1,2,3,1,2,3], k = 2
		输出: false

  （2）求解工具
		（1）暴力求解方法
			（1）计算原数组长度size
			（2）设计暴力的两个for循环嵌套
			（3）判断两个元素是否相等，且其下标之差的绝对值是否小于特定值k，若是return true
			（4）若循环运行完了也没有return，则return false
		
		（2）哈希表
			（1）计算原数组长度size
			（2）根据长度size遍历数组的全部元素，把数组下标作为哈希表的键，存入哈希表
			（3）输入哈希表的值来查询哈希表的键（下标），若存在该值则证明有重复的元素，返回非0 下标；
			（4）输入哈希表的值取出该值对应的键（下标）与当前下标做差取绝对值判断时候小于k

（2）匹配数据结构与算法工具

	（1）数据结构：数组查询、哈希表
	（2）算法：暴力求解

（3）代码实现

（1）暴力求解

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        for(int i = 0; i < nums.size(); i ++) {//计算原数组长度size，并设计暴力的两个for循环嵌套
            for(int j = i + 1; j < nums.size(); j ++) {
                if(nums[i] == nums[j] && abs(i - j) <= k) //判断两个元素是否相等，且其下标之差的绝对值是否小于特定值k，若是return true
                    return true;
            }
        }
        return false;//若循环运行完了也没有return，则return false
    }
};

（2）哈希表实现

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        unordered_map<int, int>map;
        for(int i = 0; i < nums.size(); i ++) {//计算原数组长度size，遍历数组的全部元素
            if(map.count(nums[i]) && abs(map[nums[i]] - i) <= k) {//输入哈希表的值来查询哈希表的键（下标），若存在该值则证明有重复的元素，返回非0 下标；同时，输入哈希表的值取出该值对应的键（下标）与当前下标做差取绝对值判断时候小于k
                return true;
            }
            map[nums[i]] = i;//把数组下标作为哈希表的键，存入哈希表
        }
        return false;
    }
};

（4）思想感悟及积累

（1）变量取绝对值的API函数abs(i - j)

（2）哈希表的使用
【查询】输入哈希表的值来查询哈希表的键是否存在map.count(nums[i]
【取值】输入哈希表的值取出该值对应的键map[nums[i]]
【赋值】存入哈希表map[nums[i]] = i

.
.

202. 快乐数

（1）题目理解

（1）输入
	（1）一个整数

（2）输出
	（1）判断该整数是否为快乐树，返回bool值

（3）限制条件
	「快乐数」定义：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
	然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
	如果 可以变为  1，那么这个数就是快乐数。

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	输入：n = 19
	输出：true
	解释：
	1 + 81 = 82
	64 + 4 = 68
	36 + 64 = 100
	1 + 0 + 0 = 1
	
	输入：n = 2
	输出：false

（1）哈希表的算法
	（1）把整数的个十百位数分割出来，存入一个数组内
	（2）判断改数组的长度len
	（3）定义一个哈希表，键为数字，值为该数字出现的次数
	（4）把整数和过程计算的平方和整数依次放入哈希表的键key中，并通过键key查询值，若值等于1，则证明该整数值出现过（将会导致无限循环），return false，若值不等于1，则继续循环
	（5）循环过程中若计算得到的整数值为1，则停止循环，return ture

（2）集合的算法
	（1）初始化集合set，先把整数n加入集合set
	（2）把整数n，替换为每个位置上数字的平方和，并加入集合set
	（3）重复上述过程直到出现的平方和数字为1时返回true，或者出现的平方和数字在set中时返回false

（3）匹配数据结构与算法工具
	（1）数据结构
		数组：把整数变换成数组的函数，把数组的元素变换成整数的函数
		
		哈希表：创建哈希表、插入哈希表、查询哈希表
		
		集合：创建集合、插入集合、查询集合

（3）代码实现

（1）哈希表的算法

class Solution(object):
    def isHappy(self, n: int) -> bool:

        def get_next(n):
            total_sum = 0
            while n > 0:
                n, digit = divmod(n, 10)
                total_sum += digit ** 2
            return total_sum

        seen = set()
        while n != 1 and n not in seen:
            seen.add(n)
            n = get_next(n)

        return n == 1

（2）集合的算法

（4）思想感悟及积累

（1）审题及及找规律很重要，有时候这个规律是一个数学关系
快乐数最后面能变成一个数组，且数组的元素只有0和1
思路入门:找出过程之中，重复的数字有没有再次出现，若有出现则会无线循环，若没有出现则是快乐数

（2）一些固定功能可以包装成子函数

.
.

506. 相对名次

（1）题目理解

（1）输入
	一个长度为 n 的整数数组 score
	
（2）输出
	长度为 n 的answer获奖数组 

（3）限制条件
	无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
	输入：score = [5,4,3,2,1]
	输出：["Gold Medal","Silver Medal","Bronze Medal","4","5"]
	解释：名次为 [1st, 2nd, 3rd, 4th, 5th] 
	
	输入：score = [10,3,8,9,4]
	输出：["Gold Medal","5","Bronze Medal","Silver Medal","4"]
	解释：名次为 [1st, 5th, 3rd, 2nd, 4th]

（2）算法思路
	（1）数组排序+二维vector解法
		利用二维数组做转换
	
	
	（2）数组排序+哈希表[【这个比较好】
		（1）复制一个原数组，并对数组进行排序
		（2）建立哈希表，键为分数、值为下标
		（3）把排好序的数组元素放入哈希表的键，把排好序的数组的下标对应放入哈希表的值
		（4）遍历原数组的每一个元素，把每个元素作为键查询哈希表的值（下标），同时把下标放入一个新的数组中，（这里加上一个判断，123名次用字符串代替），当遍历完成的时候，无序的分数数据就有了与其对应的名次数组

（3）代码实现
（1）数组排序+二维vector

class Solution {
public:
    vector<string> findRelativeRanks(vector<int>& score) {
        int n = score.size();//获取分数数组的长度n
        string desc[3] = {"Gold Medal", "Silver Medal", "Bronze Medal"};//定义名次的字符串
        vector<pair<int, int>> arr;//定义一个中间二维数组，第一维代表分数，第二维代表名次

        for (int i = 0; i < n; ++i) {//把分数和名次
            arr.emplace_back(make_pair(-score[i], i));
        }
        sort(arr.begin(), arr.end());//排序
        vector<string> ans(n);//定义一个名次数组
        for (int i = 0; i < n; ++i) {
            if (i >= 3) {
                ans[arr[i].second] = to_string(i + 1);
            } else {//前三名
                ans[arr[i].second] = desc[i];
            }
        }
        return ans;
    }
};

（2）数组排序+哈希表
自己实现

（4）思想感悟及积累

（1）二维数组就是一张表
注意二维的vector的读取方式arr[i].second，当然也可以用两个下标

（2）vector可以建立二维，甚至是三维的数据结构，而且vector的数据类型可以任意自己指定

---

（5）堆栈（先进后出）

20. 有效的括号

（1）题目理解

（1）输入
	（1）一个字符串

（2）输出
	（1）若是有效的字符串，输出true;若是无效的字符串，输出false;

（3）限制条件
	无

（2）解题思路

1）画图并给出思路

（1）遍历给定的字符串 s的长度,有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，
     我们可以直接返回 False，省去后续的遍历判断过程。
（2）当我们遇到一个左括号时，我们可以将这个左括号放入栈顶。
（3）当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。
此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。
如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。
为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。也可以自己写一个switch判断函数

在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。

2）题目类型分类，匹配数据结构

（1）判断奇偶性	
	奇数判断【n % 2 == 1】
	偶数判断【n % 2 == 0】

（2）字符串
	从字符串中取一个字符，for (char ch: s) {  //遍历字符串S中的每个字符
	判断字符是否为特定字符


（3）堆栈
	定义一个堆栈stack stk;
	堆栈的入栈出栈操作
		出栈 stk.pop();
		入栈stk.push(ch);

（4）哈希表
        //定义一个哈希表，建立括号的映射，键为左括号，值为右括号
        unordered_map pairs = {
            {')', '('},
            {']', '['},
            {'}', '{'}
        };

（3）代码实现

class Solution {
public:
    bool isValid(string s) {
        int n = s.size();     //获取字符串长度
        if (n % 2 == 1) {  //字符串长度为奇数，则肯定不是有效括号
            return false;
        }
        //定义一个哈希表，建立括号的映射，键为左括号，值为右括号
        unordered_map<char, char> pairs = {
            {')', '('},
            {']', '['},
            {'}', '{'}
        };
        stack<char> stk;//定义一个堆栈
        for (char ch: s) {  //遍历字符串中的每个字符
            if (pairs.count(ch)) {//若该字符在哈希表的值中
                if (stk.empty() || stk.top() != pairs[ch]) {//右括号与左括号不对应，或者根本就没有左括号
                    return false;
                }
                stk.pop();
            }
            else {                    //若该字符不在哈希表的值中
                stk.push(ch);
            }
        }
        return stk.empty();//全部遍历完成，走到这里说明已经是有效括号了
    }
};

.

155. 最小栈【堆栈】

（1）题目
设计一个支持 push ，pop ，top 操作

.
（2）审题
输入

输出

限制条件
能在常数时间内检索到最小元素的栈

.
（3）解题思路
图例

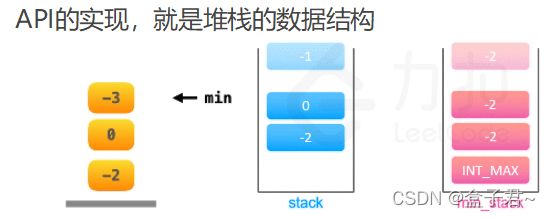
整体解题步骤
核心思想：本质是理解堆栈的数据结构，在push()时需要遍历堆栈的每一个元素找到最小值存入另外一个队列min_stack，在pop()时删除min_stack最顶层的元素，在getmin()是推出min_stack最顶层的元素

.
（4）编程实现

class MinStack {
    stack<int> x_stack;   //创建当前的堆栈
    stack<int> min_stack; //创建最小值堆栈
public:
    MinStack() {
        min_stack.push(INT_MAX);//
    }
    
    void push(int x) {
        x_stack.push(x);//当前堆栈推入一个元素
        min_stack.push(min(min_stack.top(), x));//比较当前最小值堆栈的顶层元素与当前值大仙，推入最小值
    }
    
    void pop() {    //取出操作是直接取出的
        x_stack.pop();
        min_stack.pop();
    }
    
    int top() {
        return x_stack.top();
    }
    
    int getMin() {
        return min_stack.top();
    }
};

.
（5）积累

数据结构的API也是使用类进行实现的，好像这题一样
堆栈的元素推入sta.push(num)
堆栈的元素推出sta.pop()【这里默认推出对顶层元素】
堆栈的最顶层元素的获取.xxx=sta.top()【这里注意的是获取不代表元素会推出】
获取堆栈中最小的元素xxx=sta.getmin()

---

（6）二叉树（查找）

144. 二叉树的前序遍历

【根-左-右遍历】
【递归实现】

（1）题目理解

（1）输入
	（1）一个二叉树的根节点（遍历的起始节点）
	
（2）输出
	（2）输出二叉树使用前序遍历方法遍历节点的顺序下表

（3）限制条件
	无

（2）解题思路（找规律）

输入：root = [1,null,2,3]
输出：[1,2,3]

首先我们需要了解什么是二叉树的中序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程

【递归的方法】
定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。
【注意：一遍历必须遍历到最底层的节点】【输入的根节点是一层一层来看的】

（3）代码实现

class Solution {
public:
    void preorder(TreeNode *root, vector<int> &res) {
        if (root == nullptr) {
            return;
        }
        res.push_back(root->val);
        preorder(root->left, res);
        preorder(root->right, res);
    }

    vector<int> preorderTraversal(TreeNode *root) {
        vector<int> res;
        preorder(root, res);
        return res;
    }
};

（4）思想感悟及积累

不论是数据结构还是算法，掌握基础的实现是最重要的！即数据结构掌握简单的数据结构，算法掌握常用的算法思想

94.二叉树的中遍历

【左-根-右遍历】
【递归实现】

（1）题目理解

（1）输入
	（1）一个二叉树的根节点（遍历的起始节点）
	
（2）输出
	（2）输出二叉树使用中序遍历方法遍历节点的顺序下表

（3）限制条件
	无

（2）解题思路（找规律）

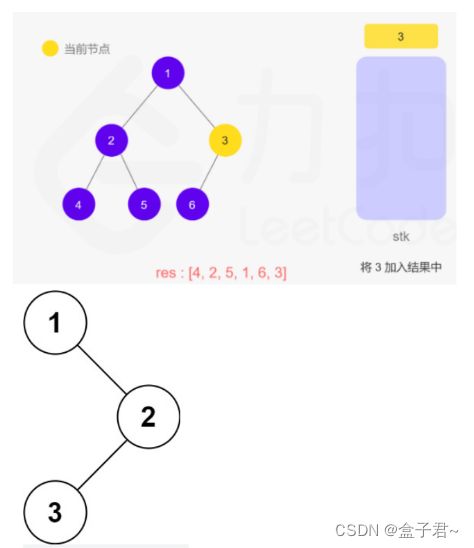
输入：root = [1,null,2,3]
输出：[1,2,3]

首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程

【递归的方法】
定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。
【注意：一遍历必须遍历到最底层的节点】【输入的根节点是一层一层来看的】

（3）代码实现

class Solution {
public:
//给定根节点，计算遍历节点的顺序数组
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root) {//若根节点为空
            return;
        }
        inorder(root->left, res);//递归实现
        res.push_back(root->val);
        inorder(root->right, res)//递归实现;
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;//定义遍历节点的顺序数组
        inorder(root, res);//给定根节点，计算遍历节点的顺序数组
        return res;
    }
};

（4）思想感悟及积累
【注意：一遍历必须遍历到最底层的节点】

145. 二叉树的后序遍历

【左-右-根遍历】
【递归实现】

（1）题目理解

（1）输入
	（1）一个二叉树的根节点（遍历的起始节点）
	
（2）输出
	（2）输出二叉树使用后序遍历方法遍历节点的顺序下表

（3）限制条件
	无

（2）解题思路（找规律）

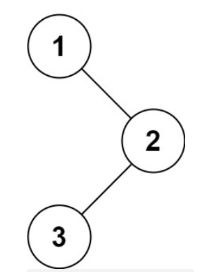
输入：root = [1,null,2,3]
输出：[3,2,1]

首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——右子树——根节点的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程

【递归的方法】
定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。
【注意：一遍历必须遍历到最底层的节点】【输入的根节点是一层一层来看的】

（3）代码实现

class Solution {
public:
    void postorder(TreeNode *root, vector<int> &res) {
        if (root == nullptr) {
            return;
        }
        postorder(root->left, res);
        postorder(root->right, res);
        res.push_back(root->val);
    }

    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        postorder(root, res);
        return res;
    }
};

（4）思想感悟及积累

不论是数据结构还是算法，掌握基础的实现是最重要的！即数据结构掌握简单的数据结构，算法掌握常用的算法思想

.

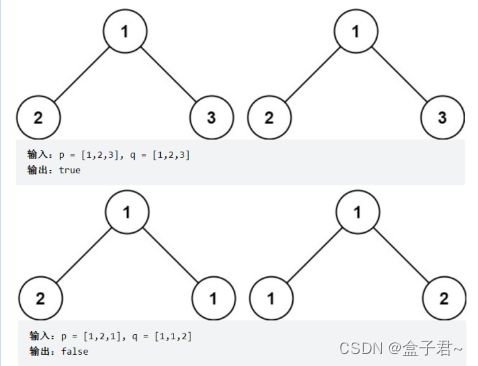
100. 相同的树【考察树的元素查询方法】

（1）题目
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
.
（2）审题

输入:两棵二叉树的根节点 p 和 q
输出:bool
限制条件:如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

.
（3）解题思路

整体解题步骤(深度优先搜索BFS)

如果两个二叉树都为空，则两个二叉树相同。如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同。
如果两个二叉树都不为空，那么首先判断它们的根节点的值是否相同，若不相同则两个二叉树一定不同，若相同，再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程，因此可以使用深度优先搜索，递归地判断两个二叉树是否相同。

.
（4）编程实现

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr) {//如果两个二叉树都为空，则两个二叉树相同
            return true;
        } else if (p == nullptr || q == nullptr) {//如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同
            return false;
        } else if (p->val != q->val) {//如果两个二叉树都不为空，那么首先判断它们的根节点的值是否相同,若不相同则两个二叉树一定不同
            return false;
        } else {//分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程
            return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
        }
    }
};

.
（5）积累

深度优先搜索BFS一般都都伴随着递归的方法
树是用指针进行进行操作的

.

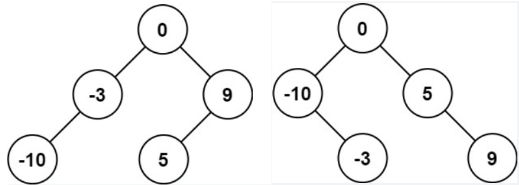
108. 将有序数组转换为二叉搜索树【数组、树】

（1）题目
给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
.
（2）审题

输入:整数数组 nums
输出:一棵 高度平衡 二叉搜索树。
限制条件:高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 的二叉树

.
（3）解题思路
图例

整体解题步骤

（1）先选择数组的中间元素作为根节点
（2）使用递归的方法分别建立左子树和右子树
（3）返回树的根节点

.
（4）编程实现

.

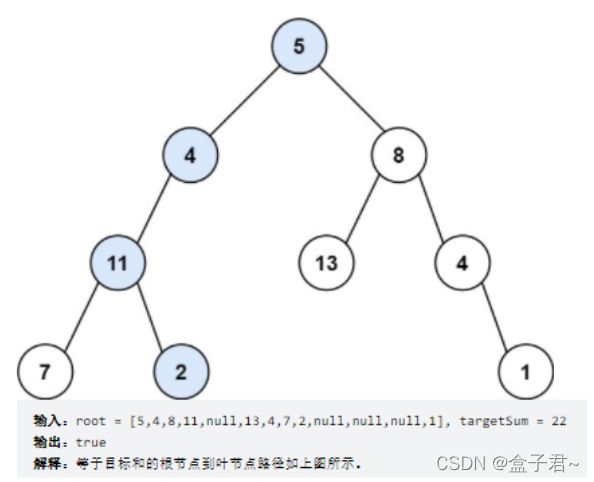
112. 路径总和【树的遍历方法】

（1）题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
.
（2）审题

输入:给你二叉树的根节点 root 和一个表示目标和的整数 targetSum
输出:判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
限制条件：无

.
（3）解题思路

整体解题步骤

核心思想是对树进行一次遍历，在遍历时记录从根节点到当前节点的路径和，以防止重复计算
广度优先搜索：我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

.
（4）编程实现

class Solution {
public:
    bool hasPathSum(TreeNode *root, int sum) {
        if (root == nullptr) {
            return false;
        }
        queue<TreeNode *> que_node;
        queue<int> que_val;
        que_node.push(root);
        que_val.push(root->val);
        while (!que_node.empty()) {
            TreeNode *now = que_node.front();
            int temp = que_val.front();
            que_node.pop();
            que_val.pop();
            if (now->left == nullptr && now->right == nullptr) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now->left != nullptr) {
                que_node.push(now->left);
                que_val.push(now->left->val + temp);
            }
            if (now->right != nullptr) {
                que_node.push(now->right);
                que_val.push(now->right->val + temp);
            }
        }
        return false;
    }
};

.
（5）积累
.

---

（7）图

（8）链表

2. 两数相加【链表、变量、数组】

（1）题目
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。请你将两个数相加，并以相同形式返回一个表示和的链表。
.
（2）审题

输入：给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，
          并且每个节点只能存储 一位 数字。

输出：将两个数相加，并以相同形式返回一个表示和的链表。

（3）解题思路
图例

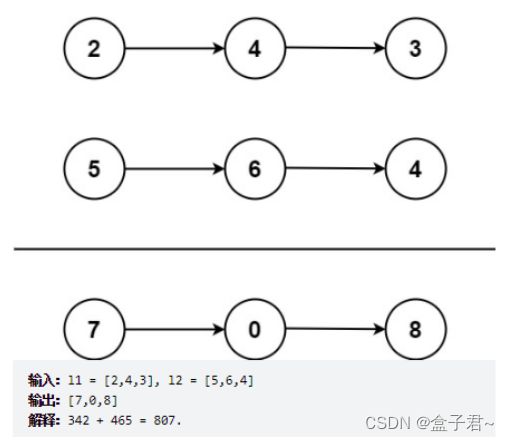
整体解题步骤
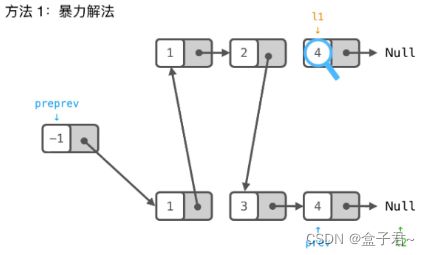
（1）解法一：暴力的解法（转换的思想）

（1）将两个链表逆序存入两个数组中【链表转数组】
（2）把两个数组按照逆序转换成两个数字并相加【数组转变量】
（3）把该相加的数字取出个位数，填充到新的求和链表中【变量转链表】

（2）解法二：通过链表进行加法进位运算

由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。

我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。
具体而言，如果当前两个链表处相应位置的数字为 n1,n2，进位值为carry，则它们的和为 n1+n2+carry；
其中，答案链表处相应位置的数字为(n1+n2+carry)mod10，而新的进位值为n1+n2+carry

如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个 00 。
此外，如果链表遍历结束后，有carry>0，还需要在答案链表的后面附加一个节点，节点的值为 carry

（4）编程实现（通过链表进行加法进位运算）

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *head = nullptr, *tail = nullptr;
        int carry = 0;
        while (l1 || l2) {
            int n1 = l1 ? l1->val: 0;
            int n2 = l2 ? l2->val: 0;
            int sum = n1 + n2 + carry;
            if (!head) {
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }
            carry = sum / 10;
            if (l1) {
                l1 = l1->next;
            }
            if (l2) {
                l2 = l2->next;
            }
        }
        if (carry > 0) {
            tail->next = new ListNode(carry);
        }
        return head;
    }
};

.

7. 整数反转【变量、数组】

（1）题目
给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

（2）审题

输入：一个 32 位的有符号整数 x
输出：返回将 x 中的数字部分反转后的结果

（3）解题思路

图例

整体解题步骤

（1）取变量中的个位数，依次存入数组中
（2）把输出的每一个元素整合成一个数字
（3）判断原来的变量正负，分别在新的变量中更改正负
优化技巧可以把数组直接省去，直接生成变量（可能思路就是没有这么清晰）

（4）编程实现

// 弹出 x 的末尾数字 digit
digit = x % 10
x /= 10

// 将数字 digit 推入 rev 末尾
rev = rev * 10 + digit

class Solution {
public:
    int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {//32位整型变量的大小限制
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            rev = rev * 10 + digit;
        }
        return rev;
    }
};

.

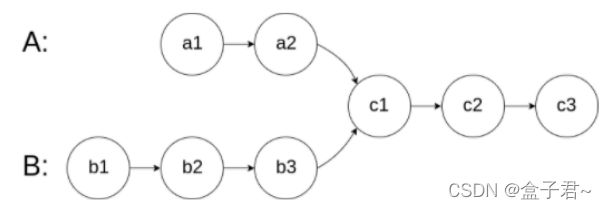
160. 相交链表【链表、集合】

（1）题目
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
.
（2）审题

输入:两个单链表的头节点 headA 和 headB【通过指针就可以知道整条链表】
输出:返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
限制条件:函数返回结果后，链表必须 保持其原始结构 。

.
（3）解题思路
图例

整体解题步骤

方法一：暴力解法（数组）
（1）通过指针把两个链表分别储存在两个数组中
（2）去第一个数组的各个元素分别遍历第二个数组，直道遍历完成第一个数组
（3）若有相同的元素则返回个元素值和两个数组的坐标

方法二：暴力解法（集合–因为不输出下标用集合也行）
（1）首先遍历链表 headA，并将链表headA 中的每个节点加入哈希集合中。然后遍历链表headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：
（2）如果当前节点不在哈希集合中，则继续遍历下一个节点；
（3）如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。
（4）如果链表headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 \text{null}null。

两种解法的核心思想是一样的，其中数组使用了遍历的方法，哈希表使用数据结构的优势
.
（4）编程实现

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode *> visited;//创建一个链表数据结构的集合
        ListNode *temp = headA;         //获取A链表的指针，用于操作
        while (temp != nullptr) {       //遍历A链表的所有元素插入到集合中
            visited.insert(temp);
            temp = temp->next;  //指向下一个元素
        }
        temp = headB;                   //获取B链表的指针
        while (temp != nullptr) {       //遍历B链表的各个元素是否与集合的元素相同
            if (visited.count(temp)) {
                return temp;
            }
            temp = temp->next;//指向下一个元素
        }
        return nullptr;
    }
};

.
（5）积累

集合操作：set.count(num)
【判断元素num是否在set集合中，若在返回true，若不在返回false】

链表没有API计算元素长度的，因为有可能是循环链表

.

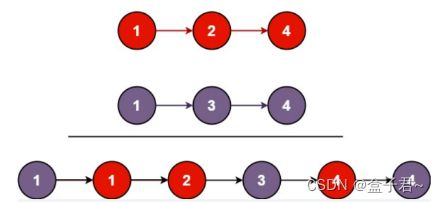
21. 合并两个有序链表【链表】

（1）题目
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
.

（2）审题

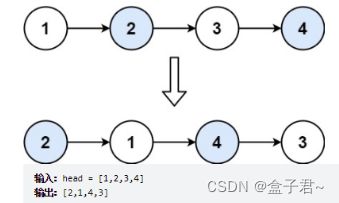
输入:两个升序链表l1 = [1,2,4], l2 = [1,3,4]
输出:合并后的一个升序链表[1,1,2,3,4,4]

.

（3）解题思路

整体解题步骤

（1）先创建一个中间链表，并把链表的指针指向-1
（2）再判断提供的两个链表的前面为遍历的元素大小，去较小的元素加入中间链表中，直到两个链表中的某一个链表为空
（3）把剩下不为空的链表的所有元素直接赋值给中间链表

.

（4）编程实现

.

（5）积累

操作链表最好使用指针
定义链表的方法 ListNode dummy=ListNode(num);
定义链表指针的方法:ListNode *prev=&dummy
判断链表是否为空:L1！=nullptr【这里的l1也是指针】
通过指针取链表的当前元素:L1->val
通过指针取链表的下一个元素:L1->next.val
链表可以相互赋值:prev->next = l1 == nullptr ? l2 : l1

.

83. 删除排序链表中的重复元素【链表】

（1）题目
给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。
.
（2）审题

输入:给定一个已排序的链表的头 head
输出:已排序且不重复的链表

.

（3）解题思路
图例

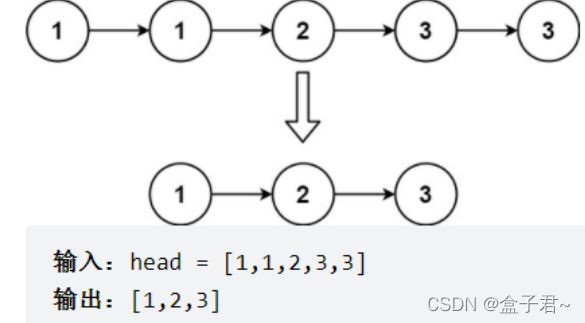
整体解题步骤
暴力解法（通过指针比较两两元素，并用指针进行赋值）
由于给定的链表是排好序的，因此重复的元素在链表中出现的位置是连续的，因此我们只需要对链表进行一次遍历，就可以删除重复的元素。
具体地，我们从指针cur 指向链表的头节点，随后开始对链表进行遍历。如果当前 cur 与cur.next 对应的元素相同，那么我们就将cur.next 从链表中移除；否则说明链表中已经不存在其它与cur 对应的元素相同的节点，因此可以将cur 指向cur.next

.

（4）编程实现

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (!head) {
            return head;
        }

        ListNode* cur = head;   //搞一个原来列表的指针进行操作
        while (cur->next) {
            if (cur->val == cur->next->val) {//若下一个链表元素等于现在链表的元素，就把下下个元素赋值为下个元素，直到元素遍历完成
                cur->next = cur->next->next;        //再这里改变了列表
            }
            else {
                cur = cur->next;
            }
        }

        return head;
    }
};

.

（5）积累

链表是需要使用指针进行操作的
ListNode* head；
ListNode* cur = head;   //搞一个原来列表的指针进行操作

.

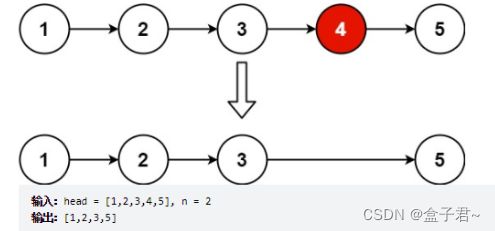
19. 删除链表的倒数第 N 个结点

（1）题目

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

（2）审题

输入：一个链表

输出：删除链表的倒数第 n 个结点，并且返回链表的头结点。

图例

（3）解题思路

1）暴力解法

（1）遍历整个链表得到链表的长度L，通过长度做差计算倒数N下标对应的正向下标（L-N+1）
（2）删除从列表开头的第（L-N+1）的元素优化操作，我们可以从（L-N+1）的元素进行删除

（2）链表数据结构转换的方法

【链表操作不熟的情况】
（1）把链表转换成数组
（2）标定倒数第N个元素不做转换
（3）把数组又转换成链表

（4）编程实现

1）暴力解法

class Solution {
public:
    int getLength(ListNode* head) {//遍历整个链表得到链表的长度L（注意计算链表长度没有API可调用）
        int length = 0;
        while (head) {
            ++length;
            head = head->next;
        }
        return length;
    }

    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(0, head);//创建一个中间链表
        int length = getLength(head);           //遍历整个链表得到链表的长度L
        ListNode* cur = dummy;                   //创建一个链表指针 
        for (int i = 1; i < length - n + 1; ++i) {//添加之前的元素
            cur = cur->next;
        }
        cur->next = cur->next->next;//删除跳过元素
        ListNode* ans = dummy->next;//一次性把后面的元素加上
        delete dummy;
        return ans;
    }
};

（5）积累

1）一般链表的问题都是从链表头进行计数的

2）遍历整个链表的操作
（注意计算链表长度没有API可调用）

int getLength(ListNode* head) {//遍历整个链表得到链表的长度L
        int length = 0;
        while (head) {
            ++length;
            head = head->next;
        }
        return length;
    }

3）创建一个中间链表的方法

ListNode* head；
ListNode* dummy = new ListNode(0, head);//创建一个中间链表

.
.

24. 两两交换链表中的节点

（1）题目

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。

（2）审题

输入：一个链表

输出：两两交换其中相邻的节点，并返回交换后链表的头节点

限制条件：你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）

（3）解题思路
图例

1）数据结构与算法匹配

	数据结构：链表
	算法：递归

2）整体解题步骤

方法一：链表转换成一个数组+双指针
	（1）把链表转换成一个数组
	（2）使用挑两格的双指针做数组的相邻元素的交换
	（3）把数组转换成链表


方法二：链表转换成两个奇偶数组
	（1）把链表转换成两个奇偶数组
	（2）根据奇偶数组组合成为一个新的链表


方法三：直接暴力递归
	递归的终止条件是链表中没有节点，或者链表中只有一个节点，此时无法进行交换。
	
	如果链表中至少有两个节点，则在两两交换链表中的节点之后，原始链表的头节点变成新的链表的第二个节点，原始链表的第二个节点变成新的链表的头节点。链表中的其余节点的两两交换可以递归地实现。在对链表中的其余节点递归地两两交换之后，更新节点之间的指针关系，即可完成整个链表的两两交换。

（4）编程实现
直接暴力递归

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {//递归的终止条件是链表中没有节点，或者链表中只有一个节点
            return head;
        }
        ListNode* newHead = head->next;//把第二个节点给第一个节点
        head->next = swapPairs(newHead->next);//符合条件，进入递归，把第一个节点给第二个节点
        newHead->next = head;
        return newHead;
    }
};

（5）积累
1）从某个元素开始复制链表

ListNode* head；//创建一个链表
ListNode* newHead = head->next;//把第二个节点开始的链表赋值给它

---

三、算法相关题型积累

（0）位运算

67. 二进制求和

（1）题目理解

（1）输入
	（1）两个用字符串表示的二进制数字

（2）输出
	（2）两个二进制数字求和，用二进制输出结果

（3）限制条件
	无

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
输入: a = “11”, b = “1”
输出: “100”

输入: a = "1010", b = "1011"
输出: "10101"

方法一：数据结构转换，变量运算，进制转换
（1）字符串数据转整形数据
（2）二进制转十进制
（3）变量运算
（4）十进制转二进制
（5）整形数据转字符串数据

方法二：位运算
（使用计算机的思维进行运算，避免了变量运算）

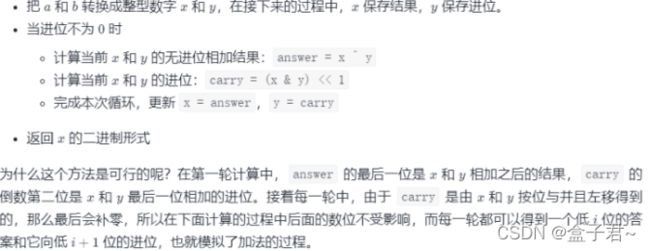
（3）代码实现

class Solution:
    def addBinary(self, a, b) -> str:
        x, y = int(a, 2), int(b, 2)
        while y:
            answer = x ^ y
            carry = (x & y) << 1
            x, y = answer, carry
        return bin(x)[2:]

.

---

（1）排序

35. 搜索插入位置

【数组排序–（插入排序和二分查找排序）】

（1）题目理解

（1）输入
	（1）一个排序的数组
	（2）一个目标值

（2）输出
	（1）若目标值在排序数组中，则输出目标值现在的下标索引
	（2）若目标值不在排序数组中，则输出目标值按排序将要插入的下标索引

（3）限制条件
	无

（2）解题思路（找规律）
（1）画图（示例）找规律并给出思路
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2

	示例 2:
	输入: nums = [1,3,5,6], target = 2
	输出: 1

方法一：暴力遍历求解
（简单好用）
	
	（1）先判断数组的长度length
	（2）正序遍历数组内的全部元素，并判断每个元素与目标值是否相等，若相等直接return下标索引即可
	（3）若上述都没有return，则表示该目标不在数组内，且是数组内最大的，直接return数组长度length

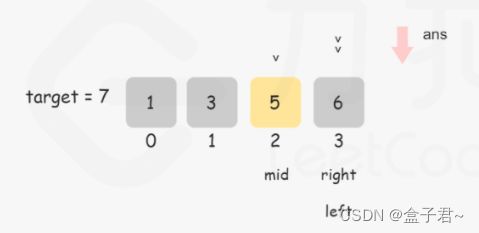
方法二：二分查找
	不断用二分法逼近查找第一个大于等于 target 的下标，ans 初值设置为数组长度可以省略边界条件的判断，因为存在一种情况是target 大于数组中的所有数，此时需要插入到数组长度的位置。

（2）匹配数据结构与算法工具
	（1）取数组元素，并进行变量判断
	（2）数组排序--插入排序或二分查找

（3）代码实现

方法一：暴力遍历求解
（简单好用）自己实现（不难）

方法二：二分查找

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();//获取数组长度
        int left = 0, right = n - 1, ans = n;//二分查找的边界条件
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;//计算中值
            if (target <= nums[mid]) {//落在左值区间
                ans = mid;//这里是和二分查找同的地方，用于获取下标或者将要插入的下标
                right = mid - 1;//修改右值
            } else {                  //落在右值区间
                left = mid + 1; //修改左值
            }
        }
        return ans;
    }
};

（4）思想感悟及积累

（1）排序和查找是算法中应用最多的
（2）二分查找和排序也可以相互借鉴

.

---

（2）查找

1、二分查找（194）

2、深度优先搜索（289）、广度优先搜索（234）

17. 电话号码的字母组合

（1）题目

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

（2）审题

输入：给定一个仅包含数字 2-9 的字符串

输出：返回所有它能表示的字母组合

限制条件：给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母

（3）解题思路

（1）图例
	示例 1：
	输入：digits = "23"
	输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
	
	示例 2：
	输入：digits = ""
	输出：[]
	
	示例 3：
	输入：digits = "2"
	输出：["a","b","c"]

（2）数据结构与算法匹配
	数组、广度优先搜索

（3）整体解题步骤

1）广度优先搜索
（1）建立数字和数组的映射关系

（2）使用多指针（多个循环）的方式进行遍历
	（1）先判断输入了多少个字符
	（2）弹出第一个数字对应的各个字母，使用暴力的方式与下一个数组对应的字母进行匹配
	【如三个for循环嵌套】

（2）深度搜索的方法

（1）建立数字和数组的映射关系

（2）建立深度优先搜索的递归函数

（3）建立主要的调用函数

（4）编程实现

（5）积累

求所有解的题目都是要用到搜索算法，查询对应字符串和数组，搜索对应树和图
（常见的搜索算法就是DFS/BFS）

深度优先搜索一般对应递归方法

广度优先搜索一般对应队列方法

一般来所，深度优先搜索比广度优先搜索更难实现一些

.
.

104. 二叉树的最大深度

（1）题目理解

（1）输入
	（1）一个二叉树

（2）输出
	（2）该二叉树的最大深度

（3）限制条件
	无

（2）解题思路（找规律）

（1）DFS用递归实现

左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1)O(1) 时间内计算出当前二叉树的最大深度。

（1）递归过程：如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为max(l,r)+1
（2）递归终止条件：递归在访问到空节点时退出。

（2）BFS的循环迭代实现
（1）我们广度优先搜索的队列里存放的是「当前层的所有节点」
（2）每次拓展下一层的时候，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展
（3）最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为ans。

（3）匹配数据结构与算法工具
（1）数据结构：二叉树
（2）算法：BFS，DFS，递归（有同类的方法）

（3）代码实现
（1）DFS用递归实现

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;//递归终止条件：递归在访问到空节点时退出。
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;//递归过程：如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为max(l,r)+1
    }
};

（2）BFS的循环迭代实现

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;//在访问到空节点时退出。
        queue<TreeNode*> Q;      //定义一个队列（这个队列是一个树形结构的队列）
        Q.push(root);                     //把二叉树存入队列
        int ans = 0;                        //定义二叉树的深度（层数）变量
        while (!Q.empty()) {
            int sz = Q.size();   //计算队列的长度
            while (sz > 0) {     //遍历队列中的每一个元素
                TreeNode* node = Q.front();//把队列的根节点存到树形结构中
                Q.pop();                               
                if (node->left) Q.push(node->left);    //扩展左子树
                if (node->right) Q.push(node->right);//扩展右子树
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};

（4）思想感悟及积累

（1）深度优先搜索
深度优先搜索一般用递归

（2）广度优先搜索
广度优先搜索一般会转换数据结构，使用队列的数据结构进行搜索

（3）二叉树
二叉树的表出

二叉树的给定形式就像一个数组，但是该数组是分层的，
对于二叉树来说，第一层只有一个元素，第二层右两个元素，第三层右4个元素
TreeNode root

二叉树的深度

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数（叶子节点是指没有子节点的节点）

.

---

（3）（双）指针

26. 删除有序数组中的重复项

（1）题目理解

（1）输入
	（1）一个有序的数组vector nums

（2）输出
	（1）无重复的有序数组
	（2）无重复的有序数组的长度

（3）限制条件
	不额外创建使用空间

（2）解题思路（找规律）

（1）暴力解法

（1）先用size（）的方式获取数组的长度
（2）遍历所有的数组元素，进行两两的相邻比较，一共进行（size-1）次
（3）若两两相邻重复，标记其Index和删除次数a（vectorde API）
（4）遍历完成后删除数组相对应index的下标，计算新数组长度(size-a)

（2）双指针解法

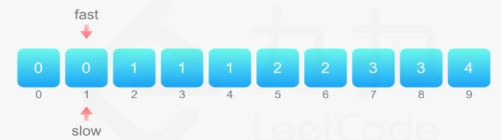
快指针用于扫描，找到重复的元素；慢指针用于指向可覆盖的位置，在原有的数组上通过迭代更改创建一个新的的数组

（1）如果数组 nums 的长度为 0，则数组不包含任何元素，因此返回 0。

（2）当数组 nums 的长度大于 0 时，数组中至少包含一个元素，在删除重复元素之后也至少剩下一个元素，因此 nums[0] 保持原状即可，从下标 1 开始删除重复元素。

定义两个指针fast 和 slow 分别为快指针和慢指针，快指针表示遍历数组到达的下标位置，慢指针表示下一个不同元素要填入的下标位置，初始时两个指针都指向下标 1。

假设数组 nums 的长度为 n。将快指针fast 依次遍历从 1 到 n−1 的每个位置，对于每个位置，如果 nums[fast] ！=nums[fast−1]，说明 nums[fast] 和之前的元素都不同，因此将nums[fast] 的值复制到 nums[slow]，然后将slow 的值加 1，即指向下一个位置。

遍历结束之后，从nums[0] 到 nums[slow−1] 的每个元素都不相同且包含原数组中的每个不同的元素，因此新的长度即为slow，返回slow 即可。

（3）代码实现
双指针解法

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();//先用size（）的方式获取数组的长度
        if (n == 0) {
            return 0;
        }
        int fast = 1, slow = 1;
        while (fast < n) {
            if (nums[fast] != nums[fast - 1]) {//快指针用于扫描，找到重复的元素,快指针判断到相邻的两个元素不一样
                nums[slow] = nums[fast];//慢指针用于指向可覆盖的位置，在原有的数组上通过迭代更改创建一个新的的数组
                ++slow;
            }
            ++fast;
        }
        return slow;
    }
};

（4）思想感悟及积累

向量vector
（1）查询向量vector长度size()
（2）读取向量vector元素at(),或者下标的方式a[0]
（3）删除向量vector元素：这里用了双指针的方式，避开了数组删除元素的复杂操作

.
.

27. 移除元素

（1）题目理解

（1）输入
	（1）一个数组nums（可重复）
	（2）一个比较的特定值value（若数组nums中的某一个元素和特定值value相同，则删除该元素）

（2）输出
	（1）不重复的新数组nums
	（2）新数组nums的长度

（3）限制条件
	不能额外创建空间

（2）解题思路（找规律）

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]

（1）判断数组的长度length
（2）创建双指针，且初始化时都指向第一个位置
（3）右（快）指针先走一步，干活用于判断与特定值value是否一致
（3）若一致则左（慢）指针不动，右（快）指针++；若不一致则左（慢）指针++，右（快）指针++，且把右（快）指针的值赋给左（慢）指针的值中；
（4）最后左（慢）指针的长度就是数组的长度

（3）代码实现

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int n = nums.size();//计算数组长度
        int left = 0;//定义左（慢）指针在第一个位置上
        for (int right = 0; right < n; right++) {//定义右（快）指针遍历数组长度
            if (nums[right] != val) {//右（快）指针若不等于特定值，左（慢）右（快）指针加一，并把右（快）指针的值赋给左（慢）指针的值中
                nums[left] = nums[right];
                left++;
            }
        }
        return left;//最后左（慢）指针的长度就是数组的长度
    }
};

（4）思想感悟及积累

双指针
快指针是干活的，慢指针是收获的，所以快指针永远比慢指针下走快一步
双指针避免一维数组的插入/删除的复杂操作的麻烦
.
.

283. 移动零

（1）题目理解

（1）输入
	（1）一个无序的整数数组

（2）输出
	（1）将所有 0元素 移动到数组的末尾，同时保持非零元素的相对顺序。

（3）限制条件
	必须在原数组上操作，不能拷贝额外的数组

（2）解题思路（找规律）

（1）画图（示例）找规律并给出思路
		[1,2,0,3,0,4,5,0]
	
	（1）方法一：暴力冒泡排序
		【方法是参考冒泡法排序的】
		（1）计算数组长度length
		（2）for循环遍历（length-1）次，每次遍历的时候遇到0元素就与下一个元素交换
	
	（2）方法二：双指针
		（1）计算数组长度length
		（2）定义一个双指针，初始化快指针fast指向数组头部，慢指针slow指向数组尾部
		（3）进行（length-1）次for循环判断快指针fast指向的元素是否为0，若元素不是为0则fast++,slow不动，若元素是为0则fast与slow对应的元素交换，然后fast++,slow--
		（4）返回排序后的数组，顺便可以判断有（length-slow）个为0 的元素

（2）匹配数据结构与算法工具
	（1）数据结构：数组
	（2）算法：1）冒泡排序、2）双指针算法

（3）代码实现

（1）方法一：暴力冒泡排序

（2）方法二：双指针

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size(), left = 0, right = 0;
        while (right < n) {
            if (nums[right]) {
                swap(nums[left], nums[right]);//两个数组的对应元素交换
                left++;
            }
            right++;
        }
    }
    };

（4）思想感悟及积累

（1）两个数组的对应元素交换：swap(nums[left], nums[right]);
（2）双指针初始化可以同时指向头部和尾部，也可以一个指向头部一个指向尾部

350. 两个数组的交集 II

（1）题目理解

（1）输入
	（1）两个整数数组num1、num2

（2）输出
	以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致
	（如果出现次数不一致，则考虑取较小值）

（3）限制条件
	可以不考虑输出结果的顺序

（2）解题思路（找规律）

（1）画图（示例）找规律
	输入：nums1 = [1,2,2,1], nums2 = [2,2]
	输出：[2,2]
	
	输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
	输出：[4,9]

（2）匹配数据结构与算法工具
	（1）数据结构：数组
	（2）算法：双指针

（3）给出算法思路

	如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。
	
	（1）首先对两个数组进行排序，然后使用两个指针遍历两个数组。
	
	（2）初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，
	如果两个数字不相等，则将指向较小数字的指针右移一位，
	如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。
	当至少有一个指针超出数组范围时，遍历结束

（3）代码实现

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size(), length2 = nums2.size();
        vector<int> intersection;
        int index1 = 0, index2 = 0;
        while (index1 < length1 && index2 < length2) {
            if (nums1[index1] < nums2[index2]) {
                index1++;
            } else if (nums1[index1] > nums2[index2]) {
                index2++;
            } else {
                intersection.push_back(nums1[index1]);
                index1++;
                index2++;
            }
        }
        return intersection;
    }
};

（4）思想感悟及积累

双指针，既可以应用在同一个数组，也可以应用在不同的两个数组中

5.最长的回文字串

（1）题目

给你一个字符串 s，找到 s 中最长的回文子串。

（2）审题

输入：字符串 s

输出：s 中最长的回文子串

限制条件：子串是原字符串中连续的字符串、回文字串的定义是从左往右读与从右往左读是一样的子串

（3）解题思路

（1）图例

	示例 1：
	输入：s = "babad"
	输出："bab"
	解释："aba" 同样是符合题意的答案。
	
	示例 2：
	输入：s = "cbbd"
	输出："bb"

（2）数据结构与算法匹配

	字符串、回文子串的检测方法

（3）整体解题步骤

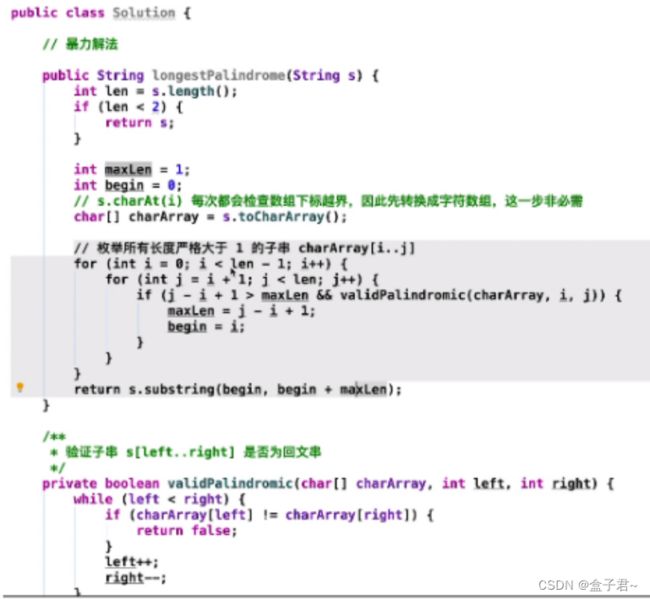
	（1）先用两个FOR循环暴力遍历字符串的两两元素
	（2）取出两两元素的下表，及其子串，判断子串是否具有回文的性质
	（3）遍历全部的长度，记录下长度最大的回文子串并输出

（4）编程实现
暴力解法

（5）积累

(1)把字符串转换为数组的API

(2)判断回文子串的方法
	使用双指针一次判断头尾两个变量是否相等，直到计算到中间变量

.

---

（4）贪心算法

53.最大子序列

（1）题目理解

（1）输入
	（1）一个无序的整数数组

（2）输出
	连续子数组的最大和

（3）限制条件
	无

（2）解题思路（找规律）

（1）暴力求解的方法

（1）先判断数组的长度length
（2）通过for循环（length-1）次，设置变量i为遍历求和相邻元素的数量，设置j为相邻元素的数量对应的遍历次数（i和j是存在关系的，实现循环嵌套）
（3）遍历完成后，return求和值最大的数

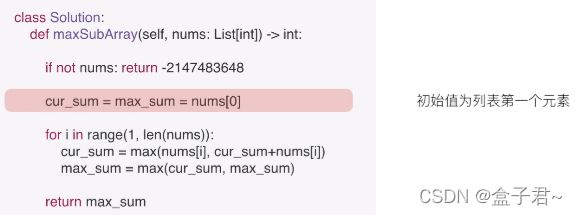
（2）贪心算法

若当前指针所指的元素之前的和小于0，则丢弃当前元素之前的数列

（3）代码实现
（1）暴力求解的方法

int maxSubArray(vector<int>& nums){
    int sum = 0;
    int length = nums.size();
    for(int i=2;i<length;i++){
        for(int j=length-1;j>0;j--){
            sum = do_sum(i,j);
        }
    }
    return sum;
}

int do_sum(int i,int j){
    int new_sum=0;
    int sum_out = 0;
    for(int a=j;a>0;a--){//控制次数
        for(int b=i;b>0;b--){//控制相邻的数量
            new_sum = new_sum + nums[b];
            if(new_sum>sum_out){
                sum_out=new_sum;
            }
        }
    }
    return sum_out;
}

（2）贪心算法

（4）思想感悟及积累

贪心算法的编写是有模板的

.

---

（5）递归

.

---

（6）动态规划

.

---

（7）回溯

.
.

四、其他的题型积累

（1）数学归纳通项

70.爬楼梯

（1）题目理解

（1）输入：
	（1）输入给定的n阶楼梯

（2）输出
	（2）爬上这个n阶楼梯有多少种方法

（3）限制条件
	每次只能爬1~2阶

（2）解题思路（找规律）

（1）动态规划的方法

（2）数学归纳通项的方法

（3）代码实现
（1）动态规划的方法

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
};

（2）数学归纳通项的方法

class Solution {
public:
    int climbStairs(int n) {
        double sqrt5 = sqrt(5);
        double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1);
        return (int)round(fibn / sqrt5);
    }
};

.
.

69. Sqrt(x)–实现x 的算术平方根

（1）题目理解

（1）输入：一个非负整数x
（2）输出：计算并返回 x 的 算术平方根 
（3）限制条件：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 

（2）解题思路（找规律）
画图（示例）找规律并给出思路

（1）方法一：【袖珍计算器算法】通过其它的数学函数代替平方根函数得到精确结果，取整数部分作为答案；

（2）方法二：【牛顿迭代法】通过数学方法得到近似结果，直接作为答案。

（3）方法三：变量的算数运算API和运算符

（3）代码实现

（1）方法一：【袖珍计算器算法】

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = exp(0.5 * log(x));
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
    }
};

（2）方法二：【牛顿迭代法】

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (fabs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return int(x0);
    }
};

（4）思想感悟及积累

变量的算数运算
关于变量的算数运算C++语言是提供了很多内置的方法API的,或者使用算数运算符也可以实现（面试背一背，平时用就查一查）【能用变量的算数运算API和运算符就用，不然要引入复杂的数学问题】

.

---

（2）数据库

.

---

（3）矩阵

.

---

（4）设计

.

---

刷题经验总结