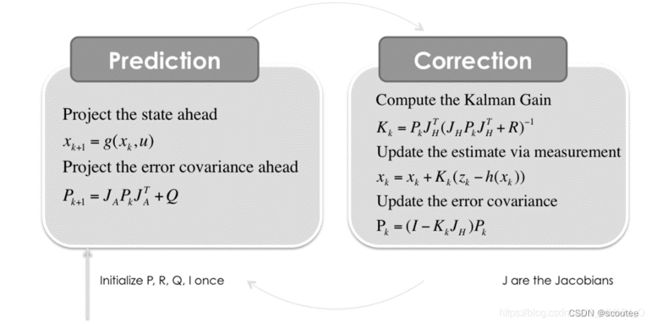
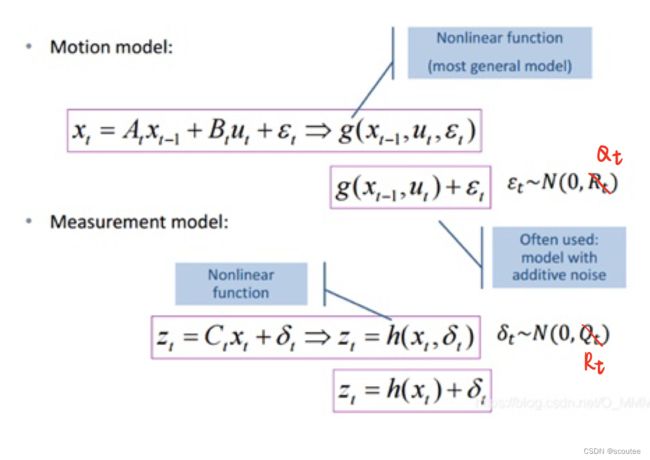
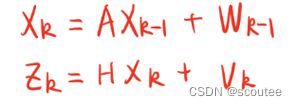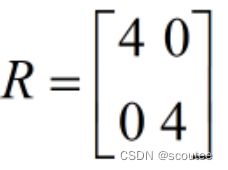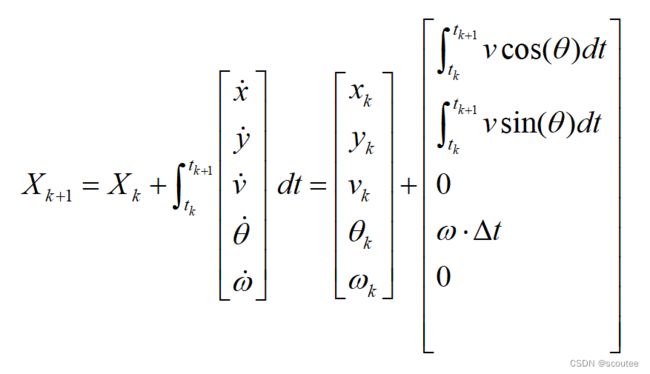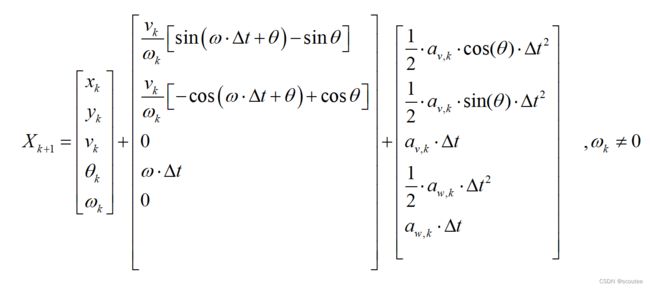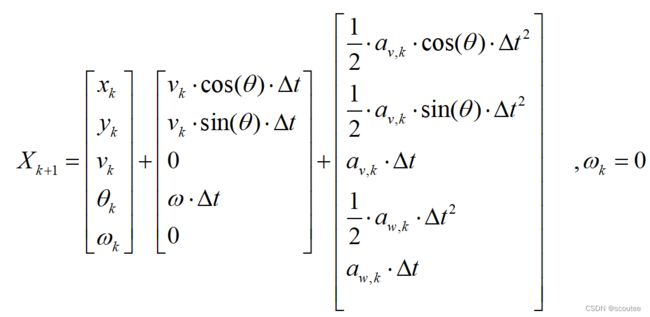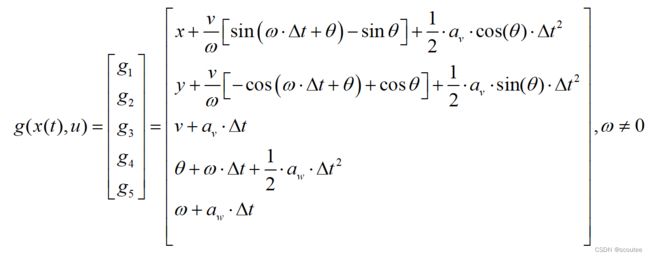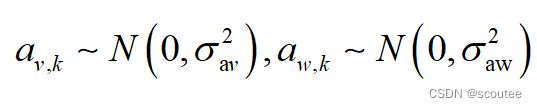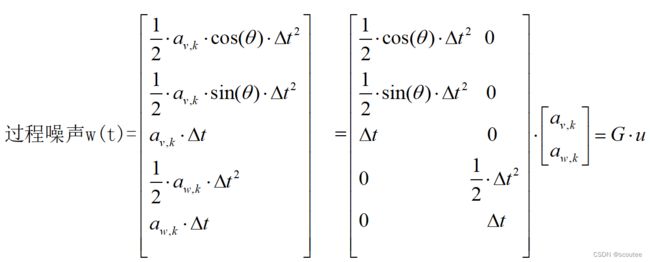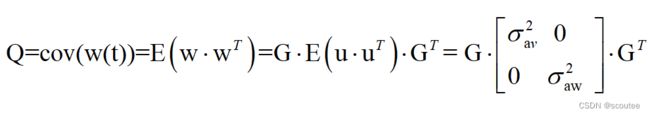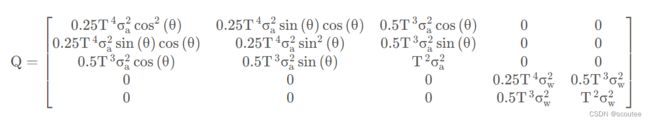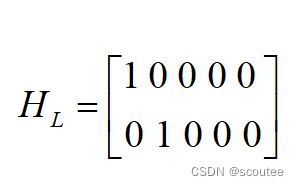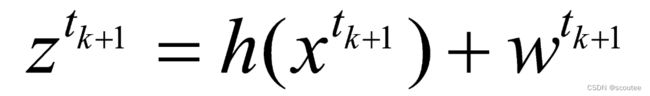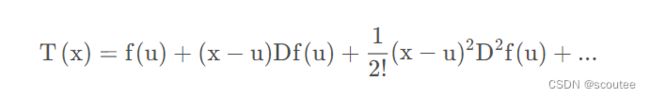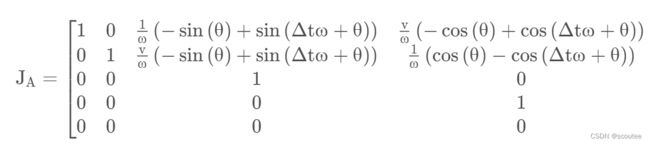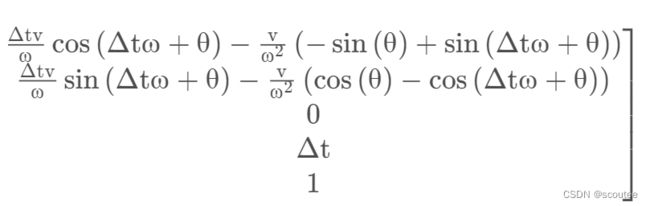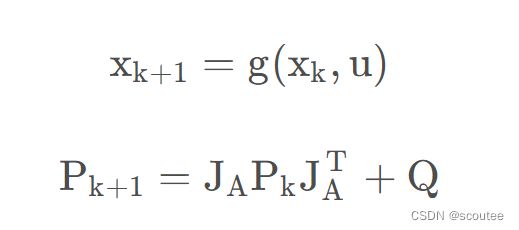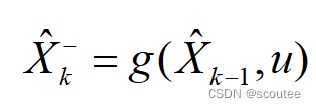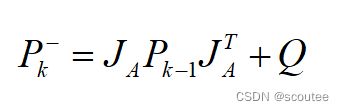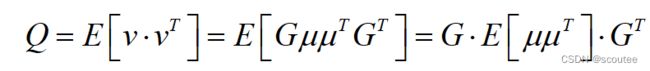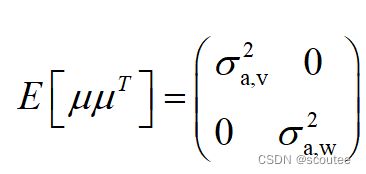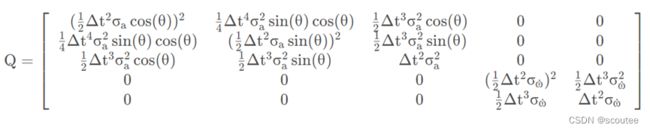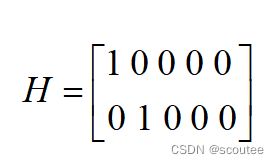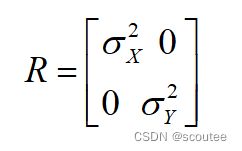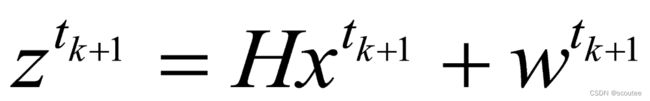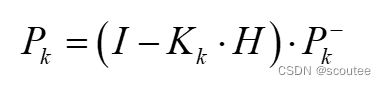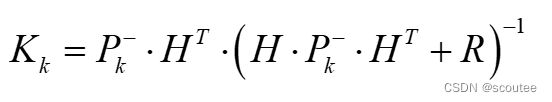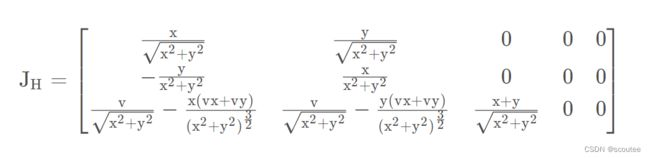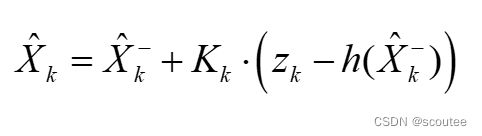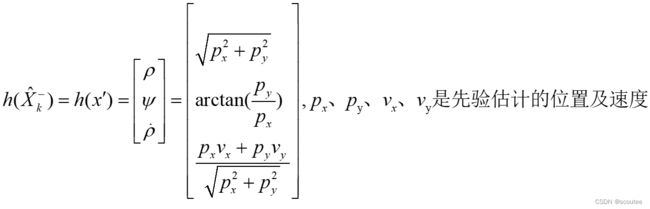滤波笔记二：运动模型（CV&CA&CTRV）

写这篇文章是因为在学习卡尔曼滤波的时候发现，只有线性运动可以用卡尔曼滤波，而非线性运动需要用到扩展卡尔曼滤波（EKF）或者无迹卡尔曼滤波（UKF）。那么又发现自己不熟悉非线性运动的运动模型，所以学了一下，并且希望用python对他们进行重现。

一些参考文章：

自动驾驶算法-滤波器系列（三）——不同运动模型（CV、CA、CTRV、CTRA）的建模和推导__归尘_的博客-CSDN博客_cv运动模型

滤波笔记二：无迹卡尔曼滤波 CTRV&&CTRA模型_泠山的博客-CSDN博客_ctra模型

3月16日 CV,CA,CTRV等运动模型，EKF，UKF在运动模型下的分析与实践_Hali_Botebie的博客-CSDN博客_ca运动模型

卡尔曼滤波理论讲解与应用（matlab和python）_O_MMMM_O的博客-CSDN博客_ekf卡尔曼滤波

扩展卡尔曼滤波（EKF）理论讲解与实例（matlab、python和C++代码）_O_MMMM_O的博客-CSDN博客_ekf python

无人驾驶汽车系统入门（二）——高级运动模型和扩展卡尔曼滤波_AdamShan的博客-CSDN博客

（组会参考）无人驾驶4： 无损卡尔曼滤波_科学边界的博客-CSDN博客

---

本文目录： 

目录

1.CV模型（Constant Velocity）恒定速度模型

2.CA模型（Constant Acceleration）恒定加速度模型

       2.1 分析算法编程需要建立的变量

2.1.1 基于状态空间表达式要建立以下变量

 2.1.2 基于卡尔曼滤波的五步迭代要建立以下变量

2.1.3 分析各个变量的初始值

2.1.4算法迭代

2.2 Python源代码

2.3 结果图分析

3.CTRV模型（Constant Turn Rate and Velocity 恒定转弯率和速度模型）

3.1 CTRV模型建模 

3.2 扩展卡尔曼滤波EKF

3.2.1 EKF的七个核心公式

 （1）建模方程和观测方程

这里挖个坑：等写完后面的公式再过来把这部分的融合写完。

（2）扩展卡尔曼滤波的迭代方程

写到这里，我终于发现了一个之前被我忽略的盲点：

最后总结一下各个过程及其表达式

（1）建模

（2）预测过程

（3）更新过程

3.3 EKF的源代码（Python）

---

1.CV模型（Constant Velocity）恒定速度模型

该模型可以参考之前的文章：滤波笔记一：卡尔曼滤波（Kalman Filtering）详解_scoutee的博客-CSDN博客

该篇文章中举了一个python实现的二维CV例子（匀速直线运动）。

2.CA模型（Constant Acceleration）恒定加速度模型

根据上述的参考文献，写了如下笔记： 

 

2.1 分析算法编程需要建立的变量

因为CA模型属于线性运动模型，所以可以直接用卡尔曼滤波。

2.1.1 基于状态空间表达式要建立以下变量

状态空间表达式（建立的是真实值）：

变量名	代码中对应值
状态变量的真实值	X_true
状态变量的分量
X坐标的真实值	position_x_true
Y坐标的真实值	position_y_true
X方向速度的真实值	speed_x_true
Y方向速度的真实值	speed_y_true
X方向加速度的真实值	acceleration_x_true
Y方向加速度的真实值	acceleration_y_true
测量值的真实值
测量值	Z
测量值的分量（均为真实值）	注意我们观察的时候，只测xy坐标两个变量
X坐标的真测量值	position_x_measure
Y坐标的真测量值	position_y_measure
X方向速度的真测量值	speed_x_measure
Y方向速度的真测量值	speed_y_measure
X方向加速度的真测量值	acceleration_x_measure
Y方向加速度的真测量值	acceleration_y_measure
噪声
过程噪声	W
X坐标的噪声	w_position_x
Y坐标的噪声	w_position_y
X方向速度的噪声	w_speed_x
Y方向速度的噪声	w_speed_y
X方向加速度的噪声	w_acceleration_x
Y方向加速度的噪声	w_acceleration_y
测量噪声	V
X坐标的测量噪声	v_position_x
Y坐标的测量噪声	v_position_y
系数矩阵
状态矩阵A	A
传输矩阵H	H

 2.1.2 基于卡尔曼滤波的五步迭代要建立以下变量

变量名	代码中对应变量
状态变量
状态变量的先验估计值	X_prior
状态变量的后验估计值	X_ posteriori
协方差矩阵
误差ek的协方差矩阵Pk	P
误差ek的协方差矩阵Pk的先验	P_prior
过程噪声w的协方差矩阵Q	Q
测量噪声v的协方差矩阵R	R
卡尔曼增益	K

2.1.3 分析各个变量的初始值

本例的代码参考了：卡尔曼滤波理论讲解与应用（matlab和python）_O_MMMM_O的博客-CSDN博客_ekf卡尔曼滤波

为了方便后续计算，设

不妨设初始位置初始速度v=5,加速度a=4,偏航角设置为

通过设置偏航角来将矢量的坐标/速度分到X轴和Y轴上。

（1）所以k-1时刻的X_true的初始值设置为：

X_true = np.array([[0],[0],[v_0 * math.cos(theta)],[v_0 * math.sin(theta)],[a_0 * math.cos(theta)],[a_0 * math.sin(theta)]])

（2）k-1时刻的状态变量的后验估计可以直接取真实值

X_posteriori = X_true

（3）过程噪声的协方差矩阵Q设置为

                                  

（4）测量噪声的协方差矩阵R设置为：

要注意我们只测量X的前两个变量，即X坐标和Y坐标。（定位更关心位置而不是速度）

                                  

即：更相信建模值，而较为不信任测量值。

（5）状态转移矩阵A:(t就是时间间隔，可以对其取值)

#状态转移矩阵，上一时刻的状态转移到当前时刻
A = np.array([[1,0,t,0,0.5*t*t,0],[0,1,0,t,0,0.5*t*t],[0,0,1,0,t,0],[0,0,0,1,0,t],[0,0,0,0,1,0],[0,0,0,0,0,1]])
#传输矩阵/状态观测矩阵H
H = np.array([[1,0,0,0,0,0],[0,1,0,0,0,0]])

 （6）注意传输矩阵H，因为我们只测量了X坐标和Y坐标，所以它的维度是2*6。

 （7）滤波误差的协方差矩阵的初始值对算法影响不大，因为算法迭代的过程，就是协方差矩阵不断变小的过程。初始值我们取：

var_p = 3
P = np.eye(6) * var_p

2.1.4算法迭代

（1）首先是要表达出真实值，注意，真实值=理论值+噪声

X状态空间：

 X_true = np.dot(A, X_true) + W

测量值：

 Z = np.dot(H, X_true) + V

（2）然后就是五步迭代，可以参考上一篇，不过多赘述。

2.2 Python源代码

import math
import numpy as np
from matplotlib import pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#-----------------创建一个函数，用来生成符合正态分布的变量------------------------
def Gaussian_variable_generator(sigma):
    y=np.random.normal(loc=0.0,scale=sigma,size=None)
    return np.array(y)

#-----------------建立变量-------------------------------------------------
# 设时间间隔为t

# 过程噪声的协方差矩阵
t=0.08
# G = np.array([1/6*t*t*t,0],[0,1/6*t*t*t],[1/2*t*t,0],[0,1/2*t*t],[t,0],[0,t])
# G1 = np.array([],[])
# 过程噪声的方差
var_q = 0.04
Q = np.eye(6) * var_q
# print(Q)
sigma_w1 = math.sqrt(Q[0,0])
sigma_w1 = np.array(sigma_w1)
sigma_w2 = math.sqrt(Q[1,1])
sigma_w2 = np.array(sigma_w2)
sigma_w3 = math.sqrt(Q[2,2])
sigma_w3 = np.array(sigma_w3)
sigma_w4 = math.sqrt(Q[3,3])
sigma_w4 = np.array(sigma_w4)
sigma_w5 = math.sqrt(Q[4,4])
sigma_w5 = np.array(sigma_w5)
sigma_w6 = math.sqrt(Q[5,5])
sigma_w6 = np.array(sigma_w6)

# 测量噪声的协方差矩阵
# 因为只有两个测量量：X坐标和Y坐标
R = np.array([[4,0],[0,4]])
sigma_v1 = math.sqrt(R[0,0])
sigma_v1 = np.array(sigma_v1)
sigma_v2 = math.sqrt(R[1,1])
sigma_v2 = np.array(sigma_v2)

#状态转移矩阵，上一时刻的状态转移到当前时刻
A = np.array([[1,0,t,0,0.5*t*t,0],[0,1,0,t,0,0.5*t*t],[0,0,1,0,t,0],[0,0,0,1,0,t],[0,0,0,0,1,0],[0,0,0,0,0,1]])
#传输矩阵/状态观测矩阵H
H = np.array([[1,0,0,0,0,0],[0,1,0,0,0,0]])

#----------------------初始化------------------------------------------

#设初始的真实值 X坐标=0 Y坐标=0 初速度v=10 加速度a=2 偏航角theta=pi/3
v_0 = 5
a_0 = 4
theta = math.pi / 3
#利用偏航角 把X_true的各个分量表达出来
X_true = np.array([[0],[0],[v_0 * math.cos(theta)],[v_0 * math.sin(theta)],[a_0 * math.cos(theta)],[a_0 * math.sin(theta)]])
print(X_true)

# position_x_true = v_0 * math.cos(theta) * t + 0.5 * a_0 * math.cos(theta) * t * t
# position_y_true = v_0 * math.sin(theta) * t + 0.5 * a_0 * math.sin(theta) * t * t
# speed_x_true = v_0 * math.cos(theta) + a_0 * math.cos(theta) * t
# speed_y_true = v_0 * math.sin(theta) + a_0 * math.sin(theta) * t
# acceleration_x_true = a_0 * math.cos(theta)
# acceleration_y_true = a_0 * math.sin(theta)


#k-1时刻的状态变量的后验估计可以直接取真实值
X_posteriori = X_true

#假设 k-1 时刻的误差的协方差矩阵为:(误差的协方差矩阵的初始值不是特别重要 反正都会收敛)
var_p = 3
P = np.eye(6) * var_p

#X Y坐标的先验估计值
position_x_prior = []
position_y_prior = []

#X Y方向的速度的先验估计值
speed_x_prior = []
speed_y_prior = []

#X Y方向的加速度的先验估计值
acceleration_x_prior = []
acceleration_y_prior = []

#测量的量只有两个：X坐标和Y坐标
#X坐标的测量量
position_x_measure = []
#Y坐标的测量量
position_y_measure = []

#X Y坐标的后验估计值
position_x_posteriori = []
position_y_posteriori = []

#X Y方向的速度的后验估计值
speed_x_posteriori = []
speed_y_posteriori = []

#X Y方向的加速度的后验估计值
acceleration_x_posteriori = []
acceleration_y_posteriori = []

#X Y坐标的真实值
position_x_true = X_true[0,0]
position_y_true = X_true[1,0]

#X Y方向的速度的后验估计值
speed_x_true = X_true[2,0]
speed_y_true = X_true[3,0]

#X Y方向的加速度的后验估计值
acceleration_x_true = X_true[4,0]
acceleration_y_true = X_true[5,0]

#误差的协方差的迹 用来看是否已经达到最小方差的估计准则了
tr_P_posterior = P[0, 0] + P[1, 1] + P[2, 2] + P[3, 3]+P[4, 4] + P[5, 5]

if __name__ == '__main__':
    #迭代次数设为30次
    for i in range(100):
    # 基于状态空间表达式要建立以下方程(这里全是真实值啊！！)
    # 这里要注意 要在循环里面生成每一次的噪声 否则噪声永远都是一个值
        w1 = Gaussian_variable_generator(sigma_w1)
        w2 = Gaussian_variable_generator(sigma_w2)
        w3 = Gaussian_variable_generator(sigma_w3)
        w4 = Gaussian_variable_generator(sigma_w4)
        w5 = Gaussian_variable_generator(sigma_w5)
        w6 = Gaussian_variable_generator(sigma_w6)
        W = np.array([[w1], [w2], [w3], [w4], [w5], [w6]])
        print(W)
    #真实值的表达式
        X_true = np.dot(A, X_true) + W
        position_x_true = np.append(position_x_true, X_true[0,0])
        position_y_true = np.append(position_y_true, X_true[1,0])
        speed_x_true = np.append(speed_x_true, X_true[2,0])
        speed_y_true = np.append(speed_y_true, X_true[3,0])
        acceleration_x_true = np.append(acceleration_x_true, X_true[4,0])
        acceleration_y_true = np.append(acceleration_y_true, X_true[5,0])

    # 测量噪声
        v1 = Gaussian_variable_generator(sigma_v1)
        v2 = Gaussian_variable_generator(sigma_v2)
        V = np.array([[v1], [v2]])

    # 测量值的表达式
        Z = np.dot(H, X_true) + V
        position_x_measure = np.append(position_x_measure, Z[0,0])
        position_y_measure = np.append(position_y_measure, Z[1,0])

# ----------------------开始循环迭代-------------------------
# ----------------------时间更新-------------------------

    # step1:基于k-1时刻的后验估计值X_posterior建模预测k时刻的系统状态先验估计值X_prior
    # 对状态变量进行先验估计
        X_prior = np.dot(A, X_posteriori)
    # 为了看到Z状态空间各个分量的先验值的变化
        position_x_prior.append(X_prior[0,0])
        position_y_prior.append(X_prior[1,0])
        speed_x_prior.append(X_prior[2,0])
        speed_y_prior.append(X_prior[3,0])
        acceleration_x_prior.append(X_prior[4,0])
        acceleration_y_prior.append(X_prior[5,0])

    # step2:基于k-1时刻的误差ek-1的协方差矩阵P_posterior和过程噪声w的协方差矩阵Q 预测k时刻的误差的协方差矩阵的先验估计值 P_prior
        P_prior = np.dot(A,np.dot(P, A.T)) + Q

# ----------------------状态更新-------------------------
    # step3:计算卡尔曼增益
        K1 = np.dot(P_prior, H.T)
        K2 = np.dot(H, np.dot(P_prior,H.T)) + R
        K = np.dot(K1, np.linalg.inv(K2))

    # step4:利用卡尔曼增益K 进行校正更新状态，得到k时刻的后验状态估计值 X_posterior
        X_posteriori = X_prior + np.dot(K, Z - np.dot(H, X_prior))
    # 把k时刻后验预测值赋给状态分量的后验预测值
    # X Y坐标的后验估计值
        position_x_posteriori.append(X_posteriori[0,0])
        position_y_posteriori.append(X_posteriori[1,0])
    # X Y方向的速度的后验估计值
        speed_x_posteriori.append(X_posteriori[2,0])
        speed_y_posteriori.append(X_posteriori[3,0])
    # X Y方向的加速度的后验估计值
        acceleration_x_posteriori.append(X_posteriori[4,0])
        acceleration_y_posteriori.append(X_posteriori[5,0])

    # step5:更新误差的协方差矩阵
        P = np.dot(np.eye(6)-np.dot(K, H), P_prior)
    # 误差的协方差矩阵的迹，迹越小说明估计越准确
        tr_P_posterior = np.append(tr_P_posterior, P[0, 0] + P[1, 1] + P[2, 2] + P[3, 3] + P[4, 4] + P[5, 5])
   # ---------------------再从step5回到step1 其实全程只要搞清先验后验 k的自增是隐藏在循环的过程中的 然后用分量speed和position的append去记录每一次循环的结果-----------------------------

    # 可视化显示 画出误差的迹 观察其是否收敛
    if True:
        # 画出1行2列的多子图

        fig, axs = plt.subplots(1,4,figsize=(20,14))

        #速度
        axs[2].plot(speed_y_true,"-",color="blue",label="Y速度真实值",linewidth="1")
        # axs[2].plot(speed_measure,"-",color="grey",label="速度测量值",linewidth="1")
        axs[2].plot(speed_y_prior,"-",color="green",label="Y速度先验估计值",linewidth="1")
        axs[2].plot(speed_y_posteriori,"-",color="pink",label="Y速度后验估计值",linewidth="1")
        axs[2].set_title("Y轴方向速度")
        axs[2].set_xlabel('k')
        axs[2].legend(loc = 'upper left')

        axs[3].plot(speed_x_true, "-", color="blue", label="X速度真实值", linewidth="1")
        # axs[2].plot(speed_measure,"-",color="grey",label="速度测量值",linewidth="1")
        axs[3].plot(speed_x_prior, "-", color="green", label="X速度先验估计值", linewidth="1")
        axs[3].plot(speed_x_posteriori, "-", color="pink", label="X速度后验估计值", linewidth="1")
        axs[3].set_title("X轴方向速度")
        axs[3].set_xlabel('k')
        axs[3].legend(loc='upper left')

        font2 = {
                 'weight': 'bold',

                 'size': 20,

                 }


        # # 位置
        x = position_x_true
        y = position_y_true
        axs[1].plot(x, y,"-",color="blue",label="位置真实值",linewidth="1")

        x1 = position_x_measure
        y1 = position_y_measure
        axs[1].plot(x1,y1,"-",color="grey",label="位置测量值",linewidth="1")

        x2 = position_x_prior
        y2 = position_y_prior
        axs[1].plot(x2,y2,"-",color="green",label="位置先验估计值",linewidth="1")

        x3 = position_x_posteriori
        y3 = position_y_posteriori
        axs[1].plot(x3,y3,"-",color="red",label="位置后验估计值",linewidth="1")
        axs[1].set_title("轨迹图",font2)
        axs[1].set_ylabel("Y坐标/m",font2)
        axs[1].set_xlabel('X坐标/m',font2)
        axs[1].legend(loc = 'upper left')


        # 误差的迹
        axs[0].plot(tr_P_posterior, "-", color="blue", label="误差的迹", linewidth="3")
        axs[0].legend(loc='upper left')
        axs[0].set_title("误差的迹", font2)


        plt.xticks(fontsize=18, fontfamily='serif')
        plt.yticks(fontsize=18, fontfamily='serif')
        plt.show()

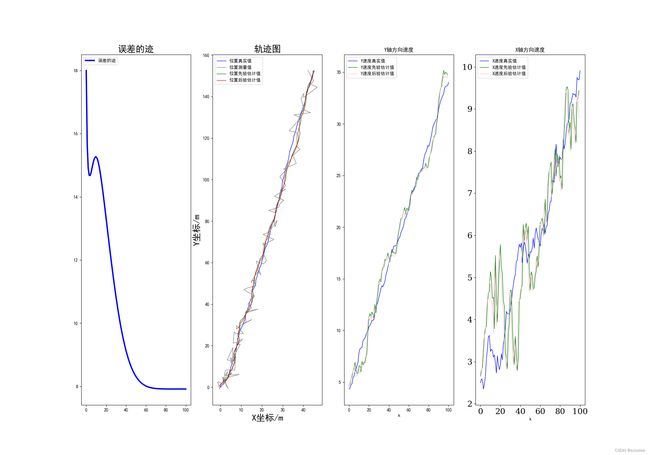
2.3 结果图分析

在当前的参数设置的情况下，可以看到真实轨迹图（蓝色）大体上符合偏航角为60°的匀加速直线运动的。灰色线条作为测量数据，偏离程度较大；绿色线条作为建模值，偏离程度较小；最后的滤波结果则是更为接近真实值，而且误差的迹也是收敛至最小值了。

然后又研究了一下速度的真实值、先验估计值、后验估计值。

当偏航角是60°时：

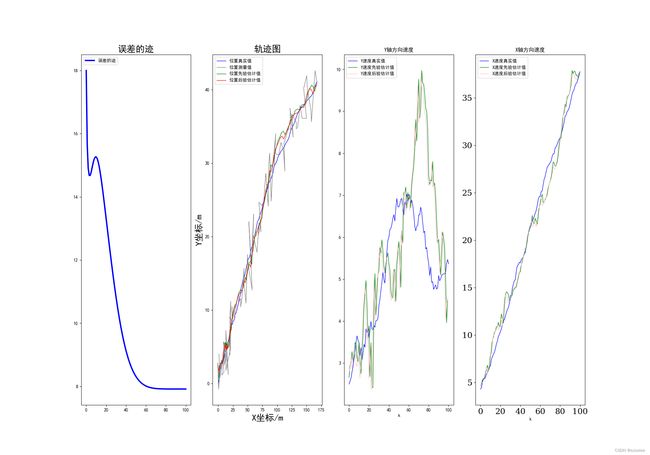
 当偏航角是30°时：

 这说明不同偏航角情况下，相当于对不同方向的加权不一样，导致受到误差的波动影响不一样。

---

-----------------------------------------以下开始非线性化模型----------------------------------------------------------

3.CTRV模型（Constant Turn Rate and Velocity 恒定转弯率和速度模型）

首先要搞清一个点：运动模型重点在于怎么建立好状态变量空间以及其状态转移函数，但是不能把运动模型和滤波算法完全混为一谈。

CTRV模型实际上是CV模型的一般形式，当角速度w=0时（需要用到洛必达法则），CTRV模型就退化成CV模型。CTRV模型假设对象沿直线前进，并且以固定的转弯速率和恒定的速度大小移动，可以看做是假设前方目标绕空间的某个点做匀加速圆周运动。

3.1 CTRV模型建模 

这个过程稍微有点复杂，我自己是觉得可以直接掌握结论，因为这个模型已经很经典了。

状态量为：v指的是速度大小

 状态方程为：其中速度v是常量，角速度w也是常量，与时间无关。

结合过程噪声，完整的状态方程：其中是径向速度v的加速度，是偏航角加速度w的加速度。

在对CTRV的运动模型建模后，就相当于我们之前在卡尔曼滤波的时候，对运动方程建好模型了，那么还需要表达出测量过程。

而且还有一个问题：卡尔曼滤波仅仅用于处理线性问题，而CTRV模型是非线性的，这个时候就不能简单的使用卡尔曼滤波进行预测和更新了，此时预测的第一步变成了如下的非线性函数：

其中，g()表示CTRV运动模型的状态转移函数，u表示建模噪声。

为了解决非线性系统的问题，引入扩展卡尔曼滤波EKF.

3.2 扩展卡尔曼滤波EKF

先来看扩展卡尔曼滤波的整个过程：

解决非线性的问题，例如后面测量会用到的毫米波雷达，是极坐标系的雷达，像这种雷达观测到的是径向距离和角度，这时候的观测矩阵H是非线性的函数（极坐标系可以转换成笛卡尔坐标系）。

KF和EKF的区别主要就是状态转移模型（EKF用来解决）和观测模型（EKF用来解决）可以是非线性的，解决非线性的问题可以使用泰勒展开式替换成线性函数。

3.2.1 EKF的七个核心公式

 （1）建模方程和观测方程

建模方程：（Motion Model）

根据之前的推导，可以知道:

很显然，g(x(t)，u)是一个多元函数，在CTRV模型之中是：（角速度等于0的时候同理）

建模过程的噪声w(t)在CTRV模型之中的表达式：

 建模过程的噪声w(t)的协方差矩阵Q：

其实在之前的KF之中，实际跑代码的时候，一般都是自己手动去设置噪声方差，但是也是可以去推导公式的。

CTRV模型之中，噪声主要来自于 （径向速度v的加速度），（偏航角加速度w的加速度），假设它们都符合高斯分布：

则有：

 噪声的协方差矩阵为：

最后的结果：

测量方程：（Measurement Model）

参考资料：扩展卡尔曼滤波EKF (baidu.com)

在建模方程和测量方程这个部分，对我来说最难理解的反而是测量方程这个地方，因为在这里即将首次遇到非线性的测量雷达——毫米波雷达。

假设我们有激光雷达和雷达两个传感器，它们分别以一定的频率来测量以下数据：

激光雷达：测量目标车辆的坐标（x,y）。需要注意的是，这里的x,y是相对于我们的车辆的坐标系，即我们的车辆为坐标系的原点，我们的车头为x轴，车的左侧为y轴。

毫米波雷达：测量目标车辆在我们车辆坐标系下与本车的距离，目标车辆与x轴的夹角,以及目标车辆与我们的相对距离变化率（本质上是目标车辆的实际速度在我们和目标车辆的连线上的分量）。

在之前线性的卡尔曼滤波器中，我们使用一个测量矩阵H来把先验预测结果映射测量空间，也就是在后验估计那里，把先验估计的值映射到了测量空间（就是测量值Z减去H*）。

卡尔曼滤波（Kalman Filtering）——（7）扩展卡尔曼滤波（EKF）一阶滤波_@曾记否的博客-CSDN博客_ekf卡尔曼滤波

我们之所以能直接这样做，是因为这个映射本身就是线性的。

而在扩展卡尔曼滤波之中，我们使用激光雷达和毫米波雷达来测量目标车辆（这个过程可以称之为传感器融合），这个时候会有两种情况：

①激光雷达[Lidar]的测量模型仍然是线性的，其测量矩阵为：

将先验预测值映射到激光雷达的测量空间：

类似于卡尔曼滤波之中的的 H* 

EKF将预测映射到激光雷达的测量空间：

即：激光雷达的从状态空间到激光雷达测量空间的转换为

其中， 

②将预测映射到毫米波雷达[Radar]的测量空间却是非线性的：

激光雷达测量的原理是光的直线传播，所以测量的时候可以直接获得障碍物在笛卡尔坐标系下x轴、y轴和z轴上的距离。

而毫米波雷达的原理是多普勒效应，它所测量的数据都是在极坐标系下的，而从极坐标映射到笛卡尔直角坐标系的过程并非线性过程。

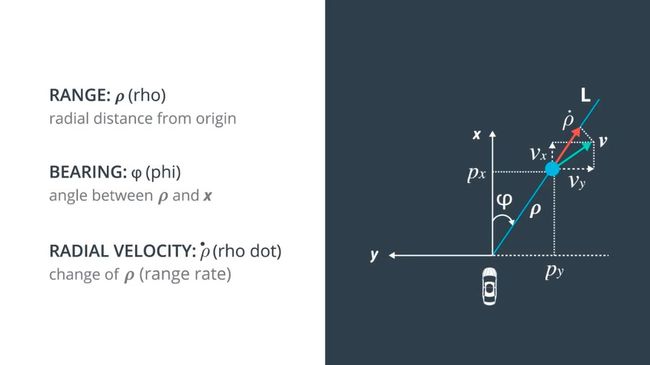
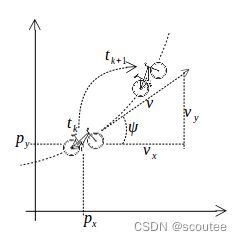
毫米波雷达能够测量障碍物在极坐标下离雷达的距离ρ、方向角ϕ以及距离的变化率（径向速度）ρ'，如下图所示。

与建模过程的多元函数g(x,u)类似，测量过程中由毫米波雷达带来的非线性映射我们使用来表示。它指定先验预测的位置和速度如何映射到范围，方位和范围速率的极坐标。

即：毫米波雷达的从状态空间到激光雷达测量空间的转换为

其中： 

③问题所在：这两种情况怎么融合呢？

其实是我自己在编程的时候，因为要先建立测量方程嘛，所以做到这里的时候实际上就不知道测量方程要怎么写了。

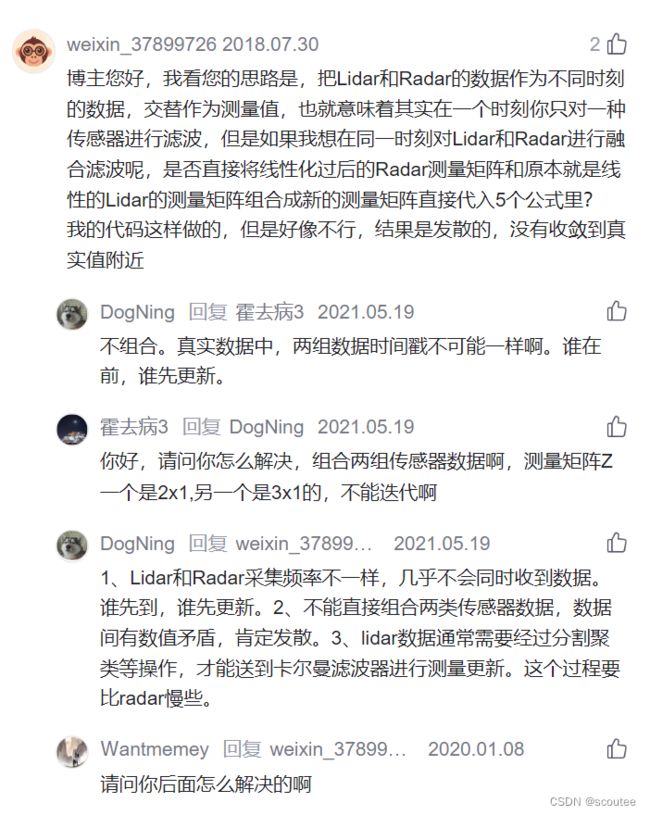
然后我在这篇文章无人驾驶汽车系统入门（二）——高级运动模型和扩展卡尔曼滤波_AdamShan的博客-CSDN博客的讨论区看到了类似的问题：——既然有两组数据，数据之间怎么融合???

从评论区的讨论里面可以看出：这篇文章里面对于用于测量的两种雷达（线性的Lidar & 非线性的Radar）的数据，是作为不同时刻的数据交替采用的。

1、Lidar和Radar采集频率不一样，几乎不会同时收到数据。谁先到，谁先更新。2、不能直接组合两类传感器数据，数据间有数值矛盾，肯定发散。3、lidar数据通常需要经过分割聚类等操作，才能送到卡尔曼滤波器进行测量更新。这个过程要比radar慢些。

然后又参考了一下：KF、EKF 和 UKF 的传感器融合，用于 CV 和 CTRV 过程模型以及激光雷达和雷达测量模型

但是这篇的源代码用的是C++写的，我看不懂。事实上感觉做雷达/车辆模型很多都是用C++。

这里挖个坑：等写完后面的公式再过来把这部分的融合写完。

（2）扩展卡尔曼滤波的迭代方程

① 初始化

初始化EKF滤波器时需要输入一个初始的状态量X，用来表示目标车辆最初的位置和速度信息，一般直接使用第一次的测量结果，或者仿真的时候直接假设一下。

②先验预测（Prediction）

在（1）建模方程和观测方程中，我们建立的方程就是真实值的表达式，其中建模噪声是有表达式的，而测量噪声一般直接认为各个分量的测量噪声符合高斯分布就可以。

现在我们来研究先验预测值的迭代公式：以下提到的F就是A矩阵。

卡尔曼滤波KF的迭代公式STEP1:

 但是在CTRV之中，过程模型（process model）是非线性的：

如果将高斯分布作为输入，输入到一个非线性函数中，得到的结果将不再符合高斯分布，也就将导致卡尔曼滤波器的公式不再适用。因此我们需要将上面的非线性函数转化为近似的线性函数求解。扩展卡尔曼滤波（EKF）的思路是利用泰勒级数展开将非线性系统线性化，然后采用卡尔曼滤波框架对信号进行滤波，因此它是一种次优滤波。

EKF通过泰勒级数展开，省略高阶项得到一个近似的线性系统。EKF只取到一阶导，同样也能有较好的结果。取一阶导时，状态转移方程和观测方程就近似为线性方程，高斯分布的变量经过线性变换之后仍然是高斯分布，这样就能够延用标准卡尔曼滤波的框架。

具体而言，EKF对于一般的非线性函数就是这样进行一阶展开的：

回到CTRV模型之中，建模过程我们已经得到了一个多元函数 X=g（x,u）

即：（w=0的时候见上文）

 那么对于这个多元函数，就需要使用多元泰勒级数：

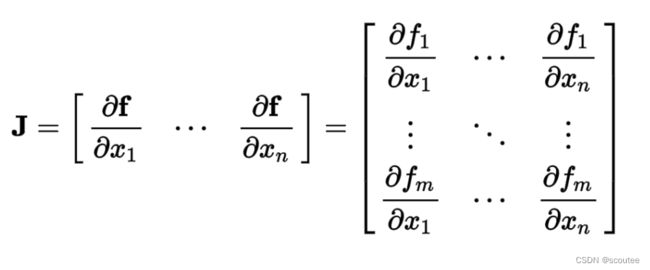
其中，Df(a)叫雅可比矩阵，它是多元函数中各个因变量关于各个自变量的一阶偏导，一般记作J。

那么在CTRV模型之中，由于x-u的数值很小，所以可以直接忽略二阶及更高阶，而只用考虑一阶偏导，所以只需要考虑雅克比矩阵。      

在CTRV模型中, 雅克比矩阵为：

算出来为：当角速度w不等于0时：

    

当角速度w=0时：

 ps:在实际编程的时候可以直接调用函数计算雅克比矩阵。 

在得到A矩阵的一阶偏导雅克比矩阵JA之后，就得到了EKF的预测部分的两个公式：

 其中，处理噪声的协方差Q在上面已经推导过为:

 ③测量更新（Measurement Update）

下面我们将基于KF的测量更新的五个公式，推导出EKF的测量更新的三个公式。

首先看第一个，计算测量值z和先验预测值x'的差值的公式，在处理类似毫米波雷达这种非线性的模型时，习惯将计算差值的公式写成：

 对应上面的式子，可以知道：

类似于g(x,u),显然h(x')也是一个非线性函数，我们也要利用泰勒一阶展开对其进行线性化，也是通过引入雅克比矩阵。卡尔曼运动模型公式推导CTRV+CTRA_GoodluckTian的博客-CSDN博客_ctra模型

而在处理激光雷达这种线性的测量系统时，不需要用雅克比矩阵，直接用H：

写到这里，我终于发现了一个之前被我忽略的盲点：

当使用的测量雷达不一样的时候，测量矩阵H（或者说JH）的矩阵大小不一样 !!!

从而导致了测量噪声协方差矩阵R的大小也不一样！！

当使用线性的激光雷达时：

噪声协方差矩阵P	5*5
状态转移矩阵	5*5
测量矩阵H	2*5
卡尔曼增益K	5*2
测量值z	2*1
先验预测值h(x')	2*1
测量噪声的协方差矩阵R	2*2

当使用非线性的毫米波雷达时：

噪声协方差矩阵P	5*5
状态转移矩阵	5*5
测量矩阵	3*5
卡尔曼增益K	5*3
测量值z	3*1
先验预测值h(x')	3*1
测量噪声的协方差矩阵R	3*3

 那么测量更新的过程就变为：

---

最后总结一下各个过程及其表达式

我发现在这一些参考资料里面，其实都忽略了先验、后验这个概念，但是写代码的时候还是挺重要的，所以自己要注意！ 

（1）建模

过程建模：（就是真实值！加了噪声那种！）

测量建模：（就是真实值！加了噪声那种！）

分两种情况——线性的激光雷达和非线性的毫米波雷达。

线性的激光雷达：注意Zk的大小是2*1,w是随机的测量噪声

非线性的毫米波雷达：注意Zk的大小是3*1

（2）预测过程

先验估计表达式： 注意先验估计是没有加噪声的啊啊啊啊啊啊啊（而且在画仿真图的时候要注意，真实轨迹应该选这种无噪的情况）

具体到CTRV模型之中：

 先验误差协方差矩阵P表达式：

具体到CTRV模型之中：

当偏航角速度w不等于0的时候：

建模噪声的协方差矩阵Q:

式中,

最后结果：

（3）更新过程

此处分两种情况：使用激光雷达测量（测量矩阵H为线性）和使用毫米波雷达测量（使用非线性函数h(x'）来映射），这两种情况我们分开来讨论，并且目前我看到的是说，这两种数据并不能很好的来做同时刻的融合，很有可能是在不同时间取不同的雷达数据。

当使用激光雷达（线性）时：

卡尔曼增益表达式：

式中，测量矩阵H: 

测量噪声协方差矩阵R一般就直接取一个常数矩阵:

后验估计表达式： 

 其中，在建模过程中已经建模了：（时间下标我没特别注意，反正k+1配k  k配k-1）

这里需要注意的是，后验估计里面的zk的表达式里面是要包含测量噪声的。

误差协方差更新表达式：

当使用毫米波雷达（非线性）时：

卡尔曼增益表达式： 

仍然为：

但是这里面的H矩阵和R矩阵的大小及意义都发生了改变。

由于毫米波雷达的预测映射到测量空间是非线性的，其表达式为：

类似于建模过程的g(x,u)，由于h(x')也是非线性的，所以EKF继续在此处引入h(x)的雅克比矩阵JH，得到此时的卡尔曼增益表达式：

其中：（实际写代码的时候可以调模块直接求雅克比矩阵） 

此时，测量噪声的协方差矩阵R变为：（大小变成3*3了）

后验估计表达式：

式中： 

 以及：

误差协方差更新表达式：

那么写到这里，就有一个绕不过去的话题：

怎么融合这两种雷达的测量数据呢？这个问题我们放到3.3源代码里面看。

3.3 EKF的源代码（Python）

3.1  仅考虑线性雷达测量的EKF IN CTRV（且角速度不为0的情况）

# 该代码参考自：https://github.com/raghuramshankar/kalman-filter-localization
# 该代码使用扩展卡尔曼滤波EKF处理非线性运动模型CTRV

# 状态空间为state matrix: x方向坐标，y方向坐标，偏航角，速度，角速度(5*1)
# 输入空间为input matrix: None
# 测量矩阵为measurement matrix:从GPS处得到的x方向坐标，y方向坐标，速度和角速度(4*1)
# 本例之中是没有采用非线性雷达的 用的是线性的雷达 所以没有出现JH

import math
import numpy as np
from matplotlib import pyplot as plt
from scipy.linalg import sqrtm
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
import numdifftools as nd

# 生成正态分布的变量
def Gaussian_variable_generator(sigma):
    y = np.random.normal(loc=0.0,scale=sigma,size=None)
    return np.array(y)

#--------------------建立变量----------------------------
# 设时间间隔为t=0.1s
dt = 0.1
# 设样本数为N，可以通过键盘输入获得
N = int(input('输入样本数量N: '))

# 测量噪声的方差(4*4的矩阵)
z_noise = np.array([[0.3,0.0,0.0,0.0],
                    [0.0,0.3,0.0,0.0],
                    [0.0,0.0,0.1,0.0],
                    [0.0,0.0,0.0,0.1]])
print(z_noise.shape)

# 先验估计值的初始值(5*1的矩阵)
x_0 = np.array([[0.0],        # x方向坐标的初始值 单位：m
                [0.0],        # y方向坐标的初始值 单位：m
                [0.0],        # 偏航角yaw的初始值 单位：rad
                [1.0],        # 速度v的初始值 单位：m/s
                [0.1]])       # 角速度 yaw rate的初始值 单位：rad/s
print(x_0.shape)

# 误差P的协方差矩阵的初始值
p_0 = np.array([[0.1, 0.0, 0.0, 0.0, 0.0],
                [0.0, 0.1, 0.0, 0.0, 0.0],
                [0.0, 0.0, 0.1, 0.0, 0.0],
                [0.0, 0.0, 0.0, 0.1, 0.0],
                [0.0, 0.0, 0.0, 0.0, 0.1]])

# 过程噪声v的协方差矩阵Q
# 由于角速度以及偏航角是用的rad弧度制 所以我们可以直接用pi表达 也可以用函数np.deg2rad(45) 把45度转换成pi/4
q = np.array([[0.00001, 0.0, 0.0, 0.0, 0.0],
              [0.0, 0.00001, 0.0, 0.0, 0.0],
              [0.0, 0.0, np.deg2rad(0.000001), 0.0, 0.0],
              [0.0, 0.0, 0.0, 1.0, 0.0],
              [0.0, 0.0, 0.0, 0.0, np.deg2rad(1.0)]])

# 测量矩阵h
# 开头说过 本例代码会从GPS处获取x坐标、y坐标、还会测速度和角速度,所以h的大小是4*5
# 根据状态空间变量的顺序，注意h的第三行是第四个元素赋1
h = np.array([[1.0, 0.0, 0.0, 0.0, 0.0],
              [0.0, 1.0, 0.0, 0.0, 0.0],
              [0.0, 0.0, 0.0, 1.0, 0.0],
              [0.0, 0.0, 0.0, 0.0, 1.0]])

# 测量噪声的协方差矩阵R
# 协方差矩阵的对角线上的数字就是该变量的方差
r = np.array([[0.015, 0.0,   0.0, 0.0],
              [0.0,   0.010, 0.0, 0.0],
              [0.0,   0.0,   0.1, 0.0],
              [0.0,   0.0,   0.0, 0.01]])**2

# 状态变量
x = []

# 生成地面的实测值gz, 以及含噪声的测量值z
# 其实从现实意义上来说 含噪声的才是真实值
# 测量值的建模过程
def gen_measurement(x_true):
    # x坐标 单位m, y坐标 单位m
    gz = h @ x_true

    # 生成含高斯白噪声的测量值z 矩阵大小为4*1
    z = gz + z_noise @ np.random.randn(4,1)
    # print('z的大小',z.shape)
    return z,gz

# -----------------扩展卡尔曼滤波非线性预测步骤 利用雅克比矩阵将非线性的过程函数线性化----------------
def extended_prediction(x,p):

    # g(x) 或者说 f(x)
    # 状态空间为state matrix: x方向坐标，y方向坐标，偏航角，速度，角速度(5*1)
    # 根据积分 求出X_k 和 X_k-1之间的关系如下：
    x[0] = x[0] + x[3]/x[4] * (np.sin(x[4] * dt + x[2]) - np.sin(x[2]))
    x[1] = x[1] + x[3]/x[4] * (-np.cos(x[4] * dt + x[2]) + np.cos(x[2]))
    x[2] = x[2] + x[4] * dt
    x[3] = x[3]
    x[4] = x[4]

# 表达一下雅克比矩阵JF里面那些比较复杂的地方
# 这里之后可以去找一下有没有更加方便的表达方法，这里我就直接写出来的
# 因为我引入了symengine包去计算偏导，但是得到的结果好像传参传不进去的感觉

    a13 = float((x[3]/x[4]) * (np.cos(x[4]*dt + x[2]) - np.cos(x[2])))
    a14 = float((1.0/x[4]) * (np.sin(x[4]*dt + x[2]) - np.sin(x[2])))
    a15 = float((dt*x[3]/x[4]) * np.cos(x[4]*dt + x[2]) -
                # 两个乘号表示的是幂运算 即x[4]的平方
                (x[3]/x[4]**2) * (np.sin(x[4]*dt +x[2]) - np.sin(x[2])))

    a23 = float((x[3]/x[4]) * (np.sin(x[4]*dt +x[2]) - np.sin(x[2])))
    a24 = float(
        (1.0/x[4]) * (-np.cos(x[4]*dt +x[2]) + np.cos(x[2]))
    )
    a25 = float(
        (dt*x[3]/x[4]) * np.sin(x[4]*dt+ x[2]) -
        (x[3]/x[4]**2) * (-np.cos(x[4]*dt +x[2]) + np.cos(x[2]))
    )

# 表达出状态转移雅克比矩阵JA(或者叫JF)
    jF = np.matrix([[1.0, 0.0, a13, a14, a15],
                    [0.0, 1.0, a23, a24, a25],
                    [0.0, 0.0, 1.0, 0.0, dt],
                    [0.0, 0.0, 0.0, 1.0, 0.0],
                    [0.0, 0.0, 0.0, 0.0, 1.0]])

#   x的先验预测值 x_pred = g(x,u)
#   即EKF的第一步

    x_pred = x

#   先验误差协方差矩阵 p_pred = jf*p*jf.T + Q
#   即EKF的第二步

    p_pred = jF @ p @ np.transpose(jF) + q

    return x_pred.astype(float), p_pred.astype(float)

#---------------------------- 扩展卡尔曼滤波线性更新过程 -----------------------------
# 更新过程的输入就是预测过程的输出，即更新过程的输入是先验预测值
def linear_update(x_pred, p_pred, z):
    # 卡尔曼增益k
    # 注意不管是线性雷达还是非线性雷达 卡尔曼增益的表达式都是一样的 只是一个是H 一个是JH
    s = h @ p_pred @ np.transpose(h) + r
    k = p_pred @ np.transpose(h) @ np.linalg.pinv(s)

    # x的后验估计值 x_upd
    v = z - h @ x_pred
    x_upd = x_pred + k @ v

    # 误差的协方差更新 p_upd
    # p_upd = p_pred - k @ h @ p_pred
    p_upd = p_pred - k @ s @ np.transpose(k)
    return x_upd.astype(float), p_upd.astype(float)

#--------------------------EKF的迭代函数-----------------------------------------------------
def extended_kalman_filter(x_est, p_est, z):
    # 预测过程中输入的x_est p_est就是上一时刻更新过程中得到的后验估计值
    x_pred, p_pred = extended_prediction(x_est,p_est)
    # 更新过程中输入的x_pred p_pred就是本时刻预测过程中得到的先验估计值
    x_upd, p_upd = linear_update(x_pred,p_pred,z)

    # 最后EKF输出的就是后验估计值 x_upd p_upd
    return x_upd, p_upd


#----------------------------------------主程序-------------------------------------------
def main():
    show_final = int(input('是否显示最终结果？(是/否 = 1/0) : '))
    show_animation = int(input('是否显示滤波器的处理过程动画？(是/否 = 1/0) : '))
    if show_animation == 1:
        show_ellipse = int(
            input('是否在动画中显示协方差椭圆？(是/否 = 1/0) : ')
        )
    else:
        show_ellipse = 0

#----------对各个变量的初始值进行赋值---------------
#  函数extended_kalman_filter的输入是上一时刻的后验估计值x_est,p_est 输出的是当前时刻的后验估计值x_upd,p_upd
#  初始化的时候，直接取x_0作为初值
    x_est = x_0
    p_est = p_0

    #x_true是真实、无噪的轨迹曲线
    x_true = x_0
    p_true = p_0

    # [x_0[0, 0], x_0[1, 0]分别是x方向的坐标和y方向的坐标
    x_true_cat = np.array([x_0[0,0], x_0[1,0]])
    x_est_cat = np.array([x_0[0,0], x_0[1,0]])
    z_cat = np.array([x_0[0,0], x_0[1,0]])
    p_est_cat = np.array([p_0[0,0]+p_0[1,1]+p_0[2,2]+p_0[3,3]+p_0[4,4]])

    for i in range(N):
        x_true, p_true = extended_prediction(x_true, p_true)
        # 经过 extended_prediction 输出的x_true是不含噪声的 p_true是加了过程噪声的

        # 生成真实测量值gz(不含噪声) 以及包含噪声的测量值z
        z, gz = gen_measurement(x_true)

        # 控制循环迭代是否停止
        if i == (N - 1) and show_final == 1:
            show_final_flag = 1
        else:
            show_final_flag = 0

        # 控制是否显示动画的函数
        postpross(i, x_true, x_true_cat, x_est, p_est, x_est_cat, z,
                  z_cat, show_animation, show_ellipse, show_final_flag)

        # 最后的后验估计值
        x_est, p_est = extended_kalman_filter(x_est, p_est, z)

        # np.vstack(): 在竖直方向上堆叠，从而达到拼接数组的作用
        # 每次进行一次循环，就会产生一组坐标的真实值，所以要利用np.vstack()函数把x_true的前两个变量拼成一个数组
        # x_true_cat 的作用好像就是用来记录 + 拼接的
        x_true_cat = np.vstack((x_true_cat, np.transpose(x_true[0:2])))
        z_cat = np.vstack((z_cat, np.transpose(z[0:2])))
        x_est_cat = np.vstack((x_est_cat, np.transpose(x_est[0:2])))
        #     我自己加的，想看一下误差的协方差矩阵的迹
        p_est_cat = np.vstack(
            (p_est_cat, (p_est[0, 0] + p_est[1, 1] + p_est[2, 2] + p_est[3, 3] + p_est[4, 4]))
        )

    print('EKF Over')
    plt.plot(p_est_cat,'b', label='误差的协方差的迹')
    plt.title('误差的协方差的迹')
    plt.show()


# ---------------------------画图模块----------------------------------------
# 动画模块
def plot_animation(i, x_true_cat, x_est_cat, z):
    # i=0 即不展示动画过程
    if i == 0:
        # 真实轨迹是红色点图
        plt.plot(x_true_cat[0], x_true_cat[1], '.r')
        # 滤波输出的结果(后验估计) 是蓝色点图
        plt.plot(x_est_cat[0], x_est_cat[1], '.b')
    else:
        # 遍历x_true_cat、x_est_cat 的x坐标和y坐标
        plt.plot(x_true_cat[0:, 0], x_true_cat[0:, 1], 'r')
        plt.plot(x_est_cat[0:, 0], x_est_cat[0:, 1], 'b')
    # 含噪声的测量值的轨迹是绿色的加号
    plt.plot(z[0], z[1], '+g')
    plt.grid(True)
    plt.pause(0.001)

# 画椭圆的模块
def plot_ellipse(x_est, p_est):
    # 在0~2pi之间取100个点
    phi = np.linspace(0, 2 * math.pi, 100)
    # 把误差的协方差矩阵的x、y坐标的部分提取出来了
    p_ellipse = np.array(
      [[p_est[0, 0], p_est[0, 1]],[p_est[1,0],p_est[1,1]]]
    )
    # sqrtm是矩阵开平方,即P=A*A,则sqrtm(P)=A
    x0 = 3 * sqrtm(p_ellipse)
    xy_1 = np.array([])
    xy_2 = np.array([])
    for i in range(100):
        arr = np.array([[math.sin(phi[i])],[math.cos(phi[i])]])
        arr = x0 @ arr
        # np.hstack(): 在水平方向上平铺
        xy_1 = np.hstack([xy_1, arr[0]])
        xy_2 = np.hstack([xy_2, arr[1]])
    plt.plot(xy_1 + x_est[0], xy_2 + x_est[1], 'y')
    plt.pause(0.00001)


def plot_final(x_true_cat, x_est_cat, z_cat):
#   x_true_cat : 真实无噪的运动轨迹
#   x_est_cat : EKF输出的后验估计值画出的运动轨迹
#   z_cat : 测量值
    fig = plt.figure()
    # 增加子图的函数，三个数字分别表示x,y,z
    f = fig.add_subplot(1,1,1)
    f.plot(x_true_cat[0:, 0], x_true_cat[0:, 1], 'r', label='真实位置')
    f.plot(x_est_cat[0:, 0], x_true_cat[0:, 1], 'b', label='后验估计位置')
    f.plot(z_cat[0:, 0], z_cat[0:, 1], '.g', label='含噪的测量值')
    f.set_xlabel('x[m]')
    f.set_ylabel('y[m]')
    f.set_title('Extended Kalman Filter - CTRV模型')
    f.legend(loc= 'upper left', shadow = True, fontsize = 'large')
    plt.grid(True)
    plt.show()

def postpross(i, x_true, x_true_cat, x_est, p_est, x_est_cat, z, z_cat, show_animation, show_ellipse, show_final_flag):
    # 如果要展示动画效果
    if show_animation == 1:
        plot_animation(i, x_true_cat, x_est_cat, z)
        if show_ellipse == 1:
            plot_ellipse(x_est[0:2], p_est)
    if show_final_flag == 1:
        plot_final(x_true_cat, x_est_cat, z_cat)

if __name__ == '__main__':
    main()

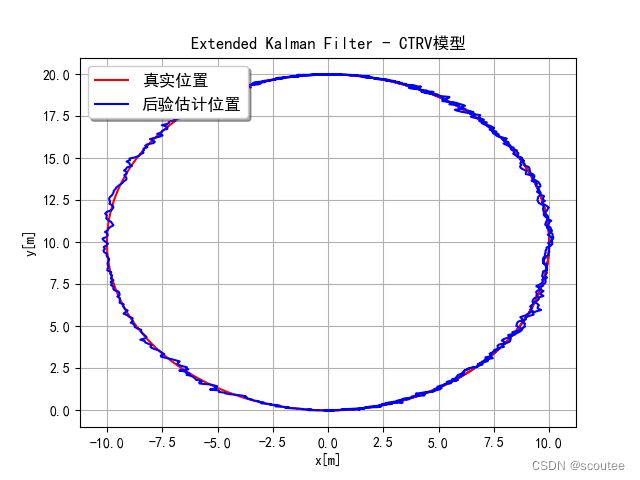
仿真结果图：

当样本数为200点时：

顺便看一下完整的轨迹图：

 注意一下，轨迹确实是一个圆形，但是由于横纵坐标显示的尺度不一样，看起来会有点像椭圆。

一些思考：

由于我自己其实更加focus在定位上面，对于径向速度或者角速度上其实我是没有那么关注的，而对于偏转角来说，实际上我只要知道位置信息就好了（x、y的位置），所以我暂时不用考虑非线性雷达测量的问题了，所以先pass.

3.2 读取自己测的卫星GPS数据