离散连续系统仿真（汽车自动停车系统和弹跳球运动模型） matlab

一、汽车自动停车系统

1.1 实验描述

汽车自动停车系统按照汽车分成三个阶段进行，第一阶段是匀减速行驶， 减速的加速度是dv/dt=-1.35（米/秒平方），当车速到达每小时20公里速度时，进入第二阶段，第二阶段也是减速行驶，减速的加速度是dv/dt=0.09t-4.36（米/秒平方），当车速到达为零时，汽车进入第三阶段，停车。车速初始速度为100公里/小时。

1.2 实验目的

使用Simulink对汽车自动停车系统进行仿真，绘制停车速度，停车距离，停车时间。

1.3 建模

1）建立这个自动停车系统的混成自动机模型：

1、离散状态集 Q={匀减速，减速，停车}；
2、连续状态集 X=R2，连续变量 x 代表二维向量（v,s）, v车辆的行驶速度，s是车辆行驶距离，它们都是时间 t 的函数；
3、向量场函数 F(·,·):{匀减速，减速，停车}×X→R2：
F(匀减速，x)=(dv∕dt=-1.35,ds/dt=v0-1.35t)，速度匀速下降；
F(减速，x)=(dv∕dt=0.09t-4.36，ds/dt=v0+0.09t2-4.36t)，车辆行驶加速度下降;
F(停车，x) =(dv/dt = 0,ds/dt=0)，车辆速度为0；
4、初始状态集 Init：{匀减速}×{v=100/3.6，s=0}；
5、域函数 Dom(·)：Q →P(X)定义为：
Dom(匀减速)={v>20/3.6}，规定 匀减速状态下车辆速度超过 20/3.6米/秒；
Dom(减速)={0 6、边集 E Q×Q：
匀减速→减速：匀减速 状态到 减速 状态有一条边，
减速→停车：减速状态到 停车状态有一条边；
7、转换条件 G(·)：E →P(X)：
（1）G(匀减速→减速) ={v=20/3.6}，从匀减速状态转换到减速状态的条件是汽车速度等于 20/3.6米/秒。
（2）G(减速→停车 )={v=0}，从减速状态转换到停车状态的条件是汽车速度等于0米/秒。
8、重置映射 R(·,·)：E×X→ P(X)：
为每个边都指定了一个空集，即没有重置动作，在状态转换过程中车辆速度变量 x不进行重置，保留变换前的值。

2）状态图

图1 汽车自动停车系统状态图

1.4 Simulink仿真

1.4.1 仿真图

图2是汽车自动停车系统stateflow状态图，最左边为匀减速状态，中间是减速状态，最右边是停车状态。v是速度，s是距离，t是时间。

图2 汽车自动停车系统stateflow图

图3是stateflow的输入和输出，v、t、s是输出，clock是时钟触发输入。

图3 stateflow中symbols

图4是simulink仿真模型，对stateflow增加了一个时钟触发事件，每0.01秒事件触发一次。将stateflow的输出连接到scope示波器上。

图4 汽车自动停车系统simulink模型

1.4.2 仿真结果

双击示波器可以看到仿真结果，如图5，蓝色是时间，黄色是车辆速度，单位为米/秒，红色是车辆行驶距离，单位米。

图5 汽车自动停车系统simulink仿真结果

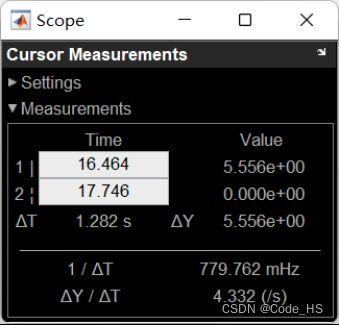
图6 汽车自动停车系统状态变化时间点
从图6中可以看到，在第一个竖线处，16.464秒处，汽车从匀减速状态转换到减速状态，在第二个竖线处，17.746处，汽车从减速状态转换为停车状态。

1.5 实验体会

通过此次实验，学习了解了simulink中子系统，时钟与示波器的使用。对于stateflow中的状态，变化方程不能写错，可以通过仿真结果图找出哪个地方出了问题。

二、弹跳球运动模型

2.1 实验描述

让球体在高度h处放下做自由落体运动，当落地时受到下落力作用，球会弹起，速度损失20%，到最高处又会受到地球引力作用做自由落体运动，这样反复落-弹运动，直到球落地不再弹起为止。

2.2 实验目的

建立弹跳球运动系统的Simulink模型，并对参数h分别等于100厘米和200厘米进行仿真。

2.3 建模

1)建立这个弹跳球运动系统的混成自动机模型：

1、离散状态集 Q={down，up}；down表示下落，up表示上升
2、连续状态集 X=R2，连续变量 x是二维向量（v,h） v代表球体的速度，往下为正，往上为负，h代表球体的高度， 都是时间 t 的函数。
3、向量场函数 F(·,·):{down，up}×X→R2：
F(down，x)=(dv∕dt=g，dh/dt=-gt)，小球下降；
F(up，v)=(dv∕dt=g，dh/dt=-v-gt)，小球上升;

4、初始状态集 Init：{down}×{v=0^h=1}；
5、域函数 Dom(·)：Q →P(X)定义为：
Dom(down)={v>=0^h>0}，规定 下降状态下弹跳球速度大于等于0并且高度大于0；
Dom(up)={v<0}，规定上升状态下弹跳球速度为负，即反向；
6、边集 E Q×Q：
down→up：down 状态到 up状态有一条边；
up→down：up 状态到 down状态有一条边；
7、转换条件 G(·)：E →P(X)：
（1）G(down→up) ={h=0}，从down状态转换到up状态的条件是球体高度等于 0。
（2）G(up→down )={v=0}，从up状态转换到down状态的条件是球体速度等于0。
8、重置映射 R(·,·)：E×V→ P(X)：R(down→up，x)={v=-0.8v}速度损失百分之二十且反向。

2)状态图

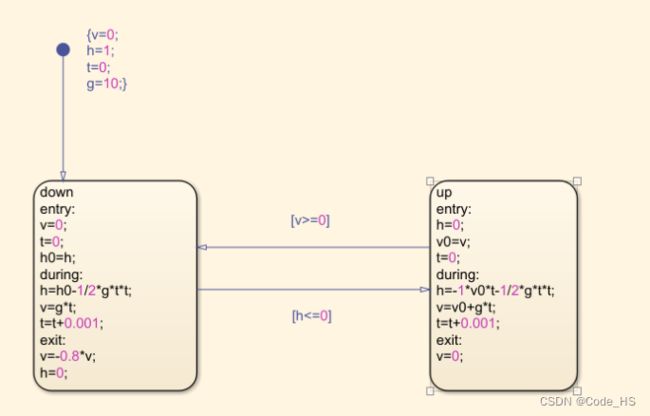
图7 弹跳球状态图

2.4 Simulink仿真

2.4.1 仿真图

在这里插入图片描述

图8 弹跳球运动 Stateflow 模型
图8是stateflow状态图，左边是down状态，右边是up状态，v代表速度，单位米/秒、t代表时间，单位秒、h代表球的高度，单位m；

图9 stateflow中symbols

图9是stateflow的输入和输出，h、v、t是输出，clock是时钟触发输入。

图10 弹跳球运动simulink模型
图10是simulink仿真图，对stateflow增加了一个时钟触发事件，每0.01秒事件触发一次。将stateflow的输出连接到scope示波器上。

2.4.2 仿真结果

1）对h等于100厘米进行仿真
横坐标代表时间，
蓝色线代表小球的速度，正数表示向下，负数表示向上，单位为米/秒；
黄色线代表弹球的高度，单位为米；
红色线代表时间，单位秒；
可以观察到弹球的高度变化为二次函数型，高度与速度逐渐缩小到0；

图11 h=100厘米时simulink仿真结果

2）对h等于200厘米进行仿真

图12 h=200厘米时simulink仿真结果

2.5 实验体会

通过此次实验，学习了解了matlab的simulink仿真，状态间的转换条件与变换状态是值的变化需要理清，不然在状态变换时，状态中的值可能会不按预期的变化发展。