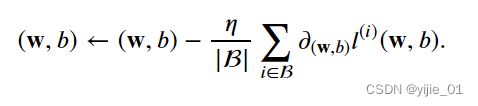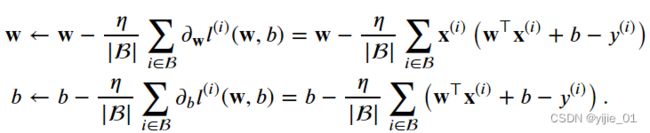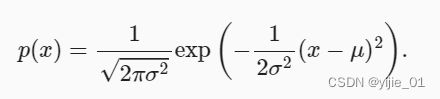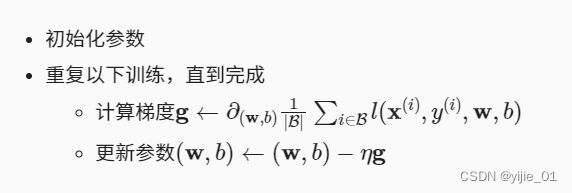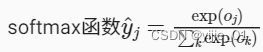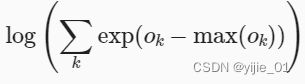动手学深度学习--线性神经网络篇

线性神经网络

前言：

该大章分为7小章节， 本章我们将介绍神经网络的整个训练过程 :

如下图顺序所示：

定义简单的神经网络架构

数据处理

指定损失函数

如何训练模型

1. linear-regression(线性回归)

NOTE:

• 回归（regression）是能为一个或多个自变量与因变量之间关系建模的一类方法： 当我们想预测一个数值时，就会涉及到回归问题
• 不是所有的 预测 都是回归问题， 分类问题的目标是预测数据属于一组类别中的哪一个
• 放射变换： 特点是通过加权和对特征进行线性变换并通过偏置项来进行平移 输出的预测值由输入特征通过线性模型的仿射变换决定，仿射变换由所选权重和偏置确定。

---

• 通过以下方法：① 一种模型质量的度量方式 ② 能够更新模型以提高模型预测质量的方法 来寻找最好的模型参数 w 与 b

展开：

①LOSS FUNCTION 损失函数 ：

• 能够 量化目标的实际值与预测值之间的差距

• 选择非负数作为损失

• 最常用的是平方误差函数
  $$l^{(i)}(\mathbf{w},b)=1/2({\hat{y}}^{(i)}-y^{(i)}{)}^2.$$

• 为了能度量 模型在整个数据集上的质量，我们需计算在训练集n个样本上的损失均值 如下式子
  

• 训练模型时，希望找到下面这组解，能够最小换在所有训练样本的总损失：

**回忆插入：**线性代数求导变换：

• 解析解： 解 w* 可以用一个公式简单地表达出来

展开：

①将偏差加入权重

上面意思为：在X的特征矩阵加上全为1的列，在W的权重矩阵加上全为偏置项b的行 这样变化后
$$X2W2==X1W1+b$$
②
$$①LOSS=1/2(Y-X2W2{)}^2$$

$$②LOS{S}^{\prime }=0$$

$$==>W^{\ast }=({\mathbf{X}}^{\top }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\top }\mathbf{y}.$$

意思是可以通过推导直接得到最佳的W *

---

• 随机梯度下降 gradient descent

展开：

①小批量随机梯度下降 minibatch stochastic gradient descent

解释：

1. 小批量
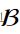
   : 由固定数量的训练样本组成的

2. 学习率

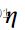
3. 偏导数

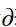
用下面的数学公式表示权重更新：

②该算法的步骤为：

随机初始化模型参数

从数据集中随机抽取小批量样本

按计算图正向计算并存入内存

反向传播得到导数值

按上式在负梯度方向更新参数

具体公式如下：

2.scratch(线性回归的从零开始实现)

章节流程图：

生成人工数据集

实现能批量读取数据集并返回一组特征与标签的函数

初始化模型参数

定义模型

定义损失函数

定义优化方法

整合模组

输入数据开始训练

基于高斯分布公式的噪声

#normal()函数为正态分布函数，定义如下：
def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

• 生成人工数据集

#torch.normal基于normal函数，生成范围(0,1) shape为
#(num_examples, len(w)的随机噪声数据
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
#此处因为w为向量，会自动调整w形状便于计算
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))
#synthetic_data()函数返回一组特征以及对应的一组标签 (一组表示多个样本)

#len函数计算第一维大小
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
#features中的每一行都包含一个二维数据样本， labels中的每一行都包含一维标签值（一个标量）

• 创建批量数据读取器

#前提 yield作用==return 返回值 并停止函数运行
#包含yield的函数  具有返回作用  同时具有迭代作用 
#如next(data_iter)
#该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels):
    num_examples = len(features)
①   indices = list(range(num_examples))
②   random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
③       batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
④       yield features[batch_indices], labels[batch_indices]
        
#为便于理解，我进行如下例子展示：
#假设batch_size=3  len(features)=1000
# ①  indices=(0,1,2,3,4.....,999)
# ②  random.shuffule(indices)后，indices=(5,23,2,546,12.....,543)的随机list
# ③  batch_indices=torch.tensor(5,23,2)
# ④  yield 返回 features中位置分别为(5,23,2)的数据和labels中位置分别为(5,23,2)的数据和
#从而实现了数据随机批量读取

• 从零实现中的参数初始化

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

---

• 定义模型

  def linreg(X, w, b):  #@save
      """线性回归模型"""
      return torch.matmul(X, w) + b
  

• 定义损失函数

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

• 定义优化算法

  此算法基于随机梯度下降实现

def sgd(params, lr, batch_size):  #@save
   """小批量随机梯度下降"""
   with torch.no_grad():
       for param in params:
           param -= lr * param.grad / batch_size
           param.grad.zero_()

• 训练 我们将执行如下过程

初始化参数

正向传播并存储中间数值

基于中间数值计算损失梯度

更新参数

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  
        # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
#解释：
#正向传播：net(X, w, b)
#l为向量，l.sum求得批量损失，l.sum().backward()进行反向传播，即求导，再将中间值存储
#sgd为基于随机梯度下降的优化算法，即更新参数，sgd不会进行求导

3.线性回归的简洁实现

简介：基于深度学习的组件，可以简化实现过程

• 读取数据集

调用框架现有的API进行读取数据

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
#data_arrays 解包  
# * 将data_arrays分解为(features, labels)
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)
#is_train表明打乱


batch_size = 10


data_iter = load_array((features, labels), batch_size)

#使用iter构造Python迭代器
iter(object[, sentinel])
#object必须是支持迭代的集合对象
#使用next从迭代器中获取第一项
next(iter(data_iter))

• 定义模型

使用Sequential类

#第一个指定输入特征形状，即2，第二个指定输出特征形状，输出特征形状为单个标量，因此为1
from torch import nn
net=nn.Sequential(nn.Linear(2,1))

• 初始化模型参数

#通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。 我们还可以使用替换方法normal_和fill_来重写参数值
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

• 定义损失函数

#计算均方误差使用的是MSELoss类，也称为L2平方范数。 默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()

• 定义优化算法

#net.parameters()从模型中获得
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

• 训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()#梯度清零防止上次的结果影响
        l.backward()#反向传播  即求导
        trainer.step()#梯度更新
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

#查看模型具体值
w = net[0].weight.dataprint('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

4.SOFTMAX回归

简介：用于分类问题

硬性类别	软性类别
属于那个类别	属于每个类别的概率

• One-Hot encoding 独热编码

类别对应的分量设置为1，其他所有分量设置为0,

例：(1,0,0)对应猫、(0,1,0)对应鸡、(0,0,1)对应狗 ：

• 网络架构

该模型具有多个输出，每个类别对应一个未规范化输出

为了简介表达，使用向量形式：

此处W为3X4的矩阵

• SoftMax运算

将输出Oi视作类i的概率的前提是：

①输出O的总和为1

②0<=Oi<=1

• 小批量样本的矢量化

• 损失函数

  交叉熵( Cross Entropy Loss)

  ①交叉熵的结果是一种期望，可以衡量模型与理想模型的差距

  ②交叉熵的结果是凸函数，更利于优化

5.图像分类数据集

采用 Fashion–MNIST数据集

6.SoftMax回归的从零开始实现

• 初始化模型参数

#Fashion-MNIST的原始数据集每个样本为1X28X28图像，共有10个类别，此处不考虑空间特征，展平为长度为784的向量(1X784)
#于是输入呈现为（NX784）
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

• 定义SoftMax操作

首先回顾.sum预算符如何沿着张量中的特定维度工作

如果X是一个形状为(2, 3)的张量，我们对列进行求和， 则结果将是一个具有形状(3,)的向量

示例代码

X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

输出为：

(tensor([[5., 7., 9.]]),
 tensor([[ 6.],
         [15.]]))

然后我们来回顾一下SoftMax的归一化：

#实现如下
def softmax(X):
    X_exp = torch.exp(X)#按元素操作x=>lnx (x∈X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

for example
X=[[1,2,3,4]]    X的shape为（1,4）
X_exp=[[ln1,ln2,ln3,ln4]]  shape为（1,4）
partition=[[ln1+ln2+ln3+ln4]] shape为（1,1）
(因为keepdim=True)
最后
X_exp / partition shape为[1,4] 
因为广播机制在运算中 将partition shape (1,1)=>相等元素的(1,4)  对应元素相除  

正如你所看到的，对于任何随机输入，我们将每个元素变成一个非负数。 此外，依据概率原理，每行总和为1。

• 定义模型

自定义的模型自动将输出softmax归一化

而高级API则在nn.CrossEntropyLoss()的损失函数中自动进行归一化

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

• 定义损失函数

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])
#range(len(y_hat))=(0,1)结合例子看
cross_entropy(y_hat, y)

举例：

y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y] #代表 y_hat (0,1)行(0,2)列的元素

result：

tensor([0.1000, 0.5000])

使用cross_entropy函数

cross_entropy(y_hat, y)

result：

tensor([2.3026, 0.6931])

• 分类精度

当我们必须输出hard-prediction(硬预测)时，通常选择预测概率最高的类

分类精度即正确预测数量与总预测数量之比

如何用代码实现计算分类精度？

前提：若y_hat为矩阵, 假定第二个维度存储每个类的预测分数

步骤：

1. 使用argmax获得每行中最大元素的索引来获得预测类别

举例：

In :       	a = np.array([[1, 3, 5, 7],[5, 7, 2, 2],[4, 6, 8, 1]])
Out: 		[[1, 3, 5, 7],
             [5, 7, 2, 2],
             [4, 6, 8, 1]]

In : 		b = np.argmax(a, axis=0)						# 对数组按列方向搜索最大值                           
Out: 		[1 1 2 0]       

In : 		b = np.argmax(a, axis=1)						# 对数组按行方向搜索最大值                           
Out: 		[3 1 2]         	

1. 将索引与真实y比较 ( “==”对数据类型敏感，因此我们将y_hat的数据类型转换为与y的数据类型一致 )
2. 因为结果是为0 or 1的tensor，所以求和得到预测正确数量

实现代码如下：

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:#如果y_hat中元素个数>1 
        y_hat = y_hat.argmax(axis=1)#获取每行最大元素的索引  索引
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

#①y_hat.type(y.dtype)将y_hat数据类型转化为y的数据类型
#② cmp = y_hat.type(y.dtype) == y 得到比较后的bool矩阵
#③ float(cmp.type(y.dtype).sum()) 
#先将cmp的bool值转化为y的数据类型并求和，然后将和转为float，便于后续精度计算

计算精度：

accuracy(y_hat, y) / len(y)
#result： 0.5
#函数运行过程解释：
#进入accuracy函数，y_hat=[2,2]因为argmax得到的是索引
#cmp=[2,2]==[0,2]
#cmp的结果为[False,Ture]
#float(cmp.type(y.dtype).sum())==1.0
#退出accuracy函数,1.0/2=0.5

同样，对于任意数据迭代器data_iter可访问的数据集， 我们可以评估在任意模型net的精度

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    #如果net为torch.nn.Module子类，则设为评估模式
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    #创建存储可以累加的存有2个数值的metric
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            #metic分别累加正确预测数、预测总数
            metric.add(accuracy(net(X), y), y.numel())
    #得到模型总分类精度
    return metric[0] / metric[1]

result：

evaluate_accuracy(net, test_iter)
=>0.0516

回忆：

①isinstance函数

isinstance()函数用来判断一个对象是否是一个已知的类型,考虑继承关系 
，认为子类是一种父类类型
语法
isinstance(object, classinfo)

参数
object -- 实例对象
classinfo -- 可以是直接或间接类名、基本类型或者由它们组成的元组

返回值
如果对象的类型与参数二的类型（classinfo）相同则返回 True，否则返回 False

示例1
a=2
isinstance(a,int) =>True
isinstance(a,str) =>False
isinstance(a,(str,int,list)) #若是元组中的一个返回True =>True

示例2
class A:
    pass
class B(A):
    pass
isinstance(A(),A) =>True
isinstance(B(),A) =>True

② net.eval or net.train函数

a) model.eval()，不启用 BatchNormalization 和 Dropout。此时pytorch会自动把BN和DropOut固定住，不会取平均，而是用训练好的值。不然的话，一旦test的batch_size过小，很容易就会因BN层导致模型performance损失较大；

b) model.train() ：启用 BatchNormalization 和 Dropout。 在模型测试阶段使用model.train() 让model变成训练模式，此时 dropout和batch normalization的操作在训练q起到防止网络过拟合的问题。

因此，在使用PyTorch进行训练和测试时一定要记得把实例化的model指定train/eval

③自行定义的Accumulator函数，用于对多个变量进行累加

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

• 训练

updater是更新模型参数的常用函数，它接受批量大小作为参数。 它可以是d2l.sgd函数，也可以是框架的内置优化函数。

def train_epoch_ch3(net,train_iter,loss,updater):
    # 将模型设置为训练模式
    if isinstance(net,torch.nn.Module):
        net.tarin()
    #创建可以累加的具有三个数值的metric
    # 训练损失总和、训练准确度总和、样本数
    metric=Accumulator(3)
    for X,y in train_iter:
        y_hat=net(X)
        l=loss(y_hat,y)
        #如果优化器为optim.Optimizer的子类
        if isinstance(updater,torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()#存储的梯度清除
            l.mean().backward()#求l梯度
            updater.step()#参数更新
        #否则
          else:
            # 使用定制的优化器和损失函数
            l.sum().backward()#求l梯度
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]
#return的第一个是 LOSS/total 第二个是 right/total

在展示训练函数的实现之前，我们定义一个在动画中绘制数据的实用程序类Animator， 它能够简化本书其余部分的代码。

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

接下来我们实现一个训练函数， 它会在train_iter访问到的训练数据集上训练一个模型net。 该训练函数将会运行多个迭代周期（由num_epochs指定）。 在每个迭代周期结束时，利用test_iter访问到的测试数据集对模型进行评估。 我们将利用Animator类来可视化训练进度。

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
#在train_epoch_ch3进行批量数据前向传播，求导，更新参数，最终返回损失精度与模型准确精度(训练集)
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
#在每次更新模型参数后，用测试集进行模型精度测试 test_acc为小数
        test_acc = evaluate_accuracy(net, test_iter)
#画出每个epoch下的损失精度与模型准确精度(训练集)与模型准确精度(测试集)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    # train_loss为损失精度 train_acc为模型准确精度(训练集)
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc
#assert 为断言句  assert condition,expression 类似 if not condition: expression
#如果不满足 condition  直接中断程序，在终端报出expression
#举例: assert train_loss < 0.5, train_loss ||if train_loss>=0.5 中断运行并报出 train_loss，else 继续向下运行

作为一个从零开始的实现，我们使用小批量随机梯度下降来优化模型的损失函数，设置学习率为0.1。

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

现在，我们训练模型10个迭代周期。 请注意，迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。 通过更改它们的值，我们可以提高模型的分类精度。

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

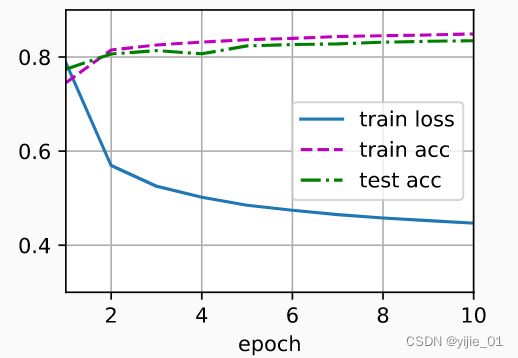
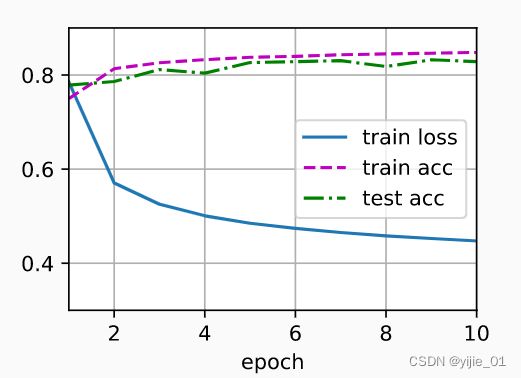
结果：

• 预测

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    #获得真实标签对应的文字标签。详细请看自定义函数d2l.get_fashion_mnist_labels 章节3.4
    trues = d2l.get_fashion_mnist_labels(y)
    #获得预测标签对应的文字标签 argmax得到数字标签，数字标签对应     文字标签
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    #titles最终呈现效果为第一行true文字标签+第二行preds文字标签
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

结果如下：

7.SoftMax的简洁实现

• 读取数据集

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)

• 初始化模型参数

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
#Flatten层用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

举例：

output.shape=3X32X64=6144

• 重新审视SoftMax的实现

​ 问题如下：
$$①Oj过大,exp(Oj)超过数据类型最大范围，造成数据溢出(上溢overflow)$$
这将使分母或分子变为inf（无穷大 )最后得到的是0、inf或nan（不是数字）的y_hat

$$②a=Oj-max(Ok)可能有较大的负值，exp(a)接近0,下溢(underflow)$$
这些值可能会四舍五入为零，使y_hat为零， 并且使得log⁡(y_hat)的值为-inf。 反向传播几步后，我们可能会发现自己面对一屏幕可怕的nan结果。

为什么不必担心？

因为∑_kexp(O_k)==∑_kexp(O_k-max(O_k)) exp(max(O_k))==1,而1>∑_kexp(O_k-max(O_k))>0，在-log_e(∑_kexp(O_k-max(O_k)))的帮助下会形成一个正数
（因水平有限，此处不能解释充分）

---

我们也希望保留传统的softmax函数，以备我们需要评估通过模型输出的概率。 但是，我们没有将softmax概率传递到损失函数中， 而是在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数

loss = nn.CrossEntropyLoss(reduction='none')
#上述意思是，在net中的softmax不再在net中进行，而是在CorssEntropyLoss中进行损失计算同时计算softmax及其对数
#为什么这么做？
#如果在net中进行sotfmax，可能存在上溢出或下溢出，虽然仍然能够正常输出，但基于此输出进行的交叉熵损失计算就会出现问题。
#所以，基于简化后的数学公式，我们直接在CorssEntropyLoss中接收未规范化的预测然后进行交叉熵计算得到损失，同时计算softmax的规范值作为最终net规范化输出

**注意：**虽然归一化和交叉熵损失都在 nn.CrossEntropyLoss进行，但交叉熵损失计算使用的是未规范化的预测，而net的输出是在nn.CrossEntropyLoss进行SoftMax之后的规范值

• 优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

• 训练

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

result：

该文章的目的是：

①作为学习笔记，方便后续回忆巩固
②详细解释高级API与整个实现过程，防止一知半解

个人数学水平有限，如有错误请指正，希望大家能与我多多交流