机器学习入门之SVM算法
SVM算法简介
- 前言
- SVM数学模型
- 凸优化求解
-
- 求其对偶问题:
- 求解其中的 α i \alpha_{i} αi
- 代码实现
- 总结
前言
支持向量机(SVM)算法是一种具有严格数学公式证明的分类算法。从简单说起,例如需要对一组二维数据 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) D={(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m})} D=(x1,y1),(x2,y2),...,(xm,ym), y i ∈ ( − 1 , + 1 ) y_{i}\in (-1,+1) yi∈(−1,+1)进行分类,如下图所示。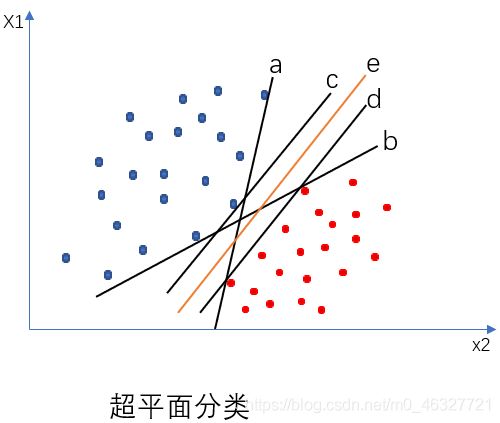
在数据集中可以划分出无数个超平面( n n n维中超平面为 n − 1 n-1 n−1维)。但是在这些超平面中只有一个超平面是最具有鲁棒性的。
鲁棒性:
就是对训练样本的局部扰动容忍度最好,也就是说在最大程度上后续添加进来的样本数据都能被正确的分类。
SVM数学模型
从图中来说其最具鲁棒性的超平面为: e e e直线。
我们假设划分超平面的线性方程是: ω T x + b = 0 \omega^{T}x+b=0 ωTx+b=0
其中 ω = ( ω 1 , ω 2 , . . . , ω d ) \omega=(\omega_{1},\omega_{2},...,\omega_{d}) ω=(ω1,ω2,...,ωd)为法向量,其决定了超平面的方向,在二维平面中相当于 1 k \frac{1}{k} k1。b为位移项,决定了超平面和原点之间的距离。由此可以计算数据中的每一个样本到超平面的距离: r = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ r=\frac{|\omega_{T}x+b|}{||\omega||} r=∣∣ω∣∣∣ωTx+b∣
我们要做的就是根据这个超平面距离公式找到最具鲁棒性的超平面。
在数据集中数据分类为 ( 0 , 1 ) (0,1) (0,1),我们将其改为 ( − 1 , + 1 ) (-1,+1) (−1,+1)。因此假设超平面能将数据正确分类,即:
{ ω T x i + b ≥ + 1 , y i = + 1 ω T x i + b ≤ − 1 , y i = − 1 \left\{ \begin{aligned} \omega^{T}x_{i}+b& \geq &+1 ,y_{i}=+1 \\ \omega^{T}x_{i}+b& \le & -1 ,y_{i}=-1\\ \end{aligned} \right. {ωTxi+bωTxi+b≥≤+1,yi=+1−1,yi=−1
我们需要做的就是找到数据中的几个样本点使得上述的等号成立,其中使得等式成立的样本点成为支持向量。通过上述的支持向量找到最大间隔使得支持向量到超平面的点最短。即如下公式:
{ m a x ω , b 2 ∣ ∣ ω ∣ ∣ s . t . y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m \left\{ \begin{aligned} max_{\omega,b}\frac{2}{||\omega||}\\ s.t. y_{i}(\omega^{T}x_{i}+b)\geq 1,i=1,2,...,m \end{aligned} \right. ⎩⎪⎨⎪⎧maxω,b∣∣ω∣∣2s.t.yi(ωTxi+b)≥1,i=1,2,...,m
在计算 ∣ ∣ ω ∣ ∣ − 1 ||\omega||^{-1} ∣∣ω∣∣−1最大值,相当于计算 ∣ ∣ ω ∣ ∣ 2 ||\omega||^{2} ∣∣ω∣∣2的最小值,于是上述公式可以改写为:
{ m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 s . t . y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m \left\{ \begin{aligned} min _{\omega,b} \frac{1}{2}||\omega||^2\\ s.t. y_{i}(\omega^{T}x_{i}+b)\geq 1,i=1,2,...,m \\ \end{aligned} \right. ⎩⎨⎧minω,b21∣∣ω∣∣2s.t.yi(ωTxi+b)≥1,i=1,2,...,m
凸优化求解
求其对偶问题:
计算上述公式,可以使用拉格朗日乘子法得到其对偶问题,对 s . t . s.t. s.t.约束条件添加拉格朗日乘子 α i ≥ 0 \alpha_{i}\geq0 αi≥0
m a x α [ Σ i = 1 m α i − 1 2 Σ i = 1 m Σ j = 1 m α i α j y i y j x i T x j ] s . t . Σ i = 1 m α i y i = 0 α i ≥ 0 , i = 1 , 2 , . . . , m max_{\alpha}[\Sigma^{m}_{i=1}\alpha_{i}-\frac{1}{2}\Sigma^{m}_{i=1}\Sigma^{m}_{j=1}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}]\\ s.t. \Sigma^{m}_{i=1}\alpha_{i}y_{i}=0\\ \alpha_{i}\geq0,i=1,2,...,m maxα[Σi=1mαi−21Σi=1mΣj=1mαiαjyiyjxiTxj]s.t.Σi=1mαiyi=0αi≥0,i=1,2,...,m
解出的 α i \alpha_{i} αi需要满足KTT(Karush-Kulu-Tucker)条件:
{ α i ≥ 0 y i f ( x i ) − 1 ≥ 0 α i ( y i f ( x i ) − 1 ) = 0 \left\{ \begin{aligned} \alpha_{i} \geq0\\ y_{i}f(x_{i})-1\geq0\\ \alpha_{i}(y_{i}f(x_{i})-1)=0 \end{aligned} \right. ⎩⎪⎨⎪⎧αi≥0yif(xi)−1≥0αi(yif(xi)−1)=0
解出 α \alpha α之后,求出 ω \omega ω与b得到模型:
f ( x ) = ω T x + b = ∑ i = 1 m α i y i x i T x + b f(x) = \omega^{T}x+b = \overset{m}{\underset{i=1}{\sum}}\alpha_{i}y_{i}x_{i}^{T}x+b f(x)=ωTx+b=i=1∑mαiyixiTx+b
然而对于线性不可分问题,即在原始样本空间内也许并不存在一个能正确划分两类样本的超平面。对于这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得这个样本在这个特征空间内线性可分。令 ϕ ( x ) \phi(x) ϕ(x)表示将x映射后的特征向量,于是在高维特征空间中划分超平面对应的模型表示为:
f ( x ) = ω T ϕ ( x ) + b f(x) = \omega^T\phi(x)+b f(x)=ωTϕ(x)+b
其中 ω \omega ω和b是模型参数,类似的有:
m i n ω , b 1 2 ∥ ω ∥ 2 s . t . y i ( ω T ϕ ( x i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m \underset{\omega,b}{min} \frac{1}{2}\Vert\omega\Vert^2\\ s.t. y_{i}(\omega^{T}\phi(x_{i})+b)\geq1 , i = 1,2,...,m ω,bmin21∥ω∥2s.t.yi(ωTϕ(xi)+b)≥1,i=1,2,...,m
其相应的对偶问题为:
m a x α [ ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) ] s . t . ∑ i = 1 m α i y i = 0 α i ≥ 0 , i = 1 , 2 , . . . , m \underset{\alpha}{max} [ \overset{m}{\underset{i=1}{\sum}}\alpha_{i} - \frac{1}{2} \overset{m}{\underset{i=1}{\sum}} \overset{m}{\underset{j=1}{\sum}} \alpha_{i} \alpha_{j} y_{i}y_{j}\phi(x_{i})^{T}\phi(x_{j}) ] \\ s.t.\overset{m}{\underset{i=1}{\sum}}\alpha_{i}y_{i}=0\\ \alpha_{i}\geq0,\qquad i = 1,2,...,m αmax[i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)]s.t.i=1∑mαiyi=0αi≥0,i=1,2,...,m
求解后即可得到函数模型:
f ( x ) = ω T ϕ ( x ) + b = ∑ i = 1 m α i y i K ( x i , x ) + b f(x) = \omega^T\phi(x)+b =\overset{m}{\underset{i=1}{\sum}}\alpha_{i}y_{i}K(x_{i},x)+b f(x)=ωTϕ(x)+b=i=1∑mαiyiK(xi,x)+b
SVM算法从线性分类到非线性分类的推广,需要将原始样本空间映射到高维特征空间,在高维特征空间中使用线性分类器分类。从低维空间到高维空间的映射需要使用到核函数。在SVM算法中,使用不同的核函数算法,其准确率和稳定性也不同。目前常用的核函数有如下表所示:
| 名称 | 表达式 |
|---|---|
| 线性核 | K ( x i , x j ) = x i T x j K(x_{i},x_{j})=x_{i}^Tx_{j} K(xi,xj)=xiTxj |
| 多项式核 | $K(x_{i},x_{j}) = (x_{i}Tx_{j})d $ |
| 高斯核 | K ( x i , x j ) = e x p ( − ∥ x i − x j ∥ 2 2 σ 2 ) K(x_{i},x_{j}) = exp(-\dfrac{\Vert x_{i}-x_{j}\Vert^2}{2\sigma^2}) K(xi,xj)=exp(−2σ2∥xi−xj∥2) |
| 拉普拉斯核 | K ( x i , x j ) = e x p ( − ∥ x i − x j ∥ 2 σ ) K(x_{i},x_{j}) = exp(-\dfrac{\Vert x_{i}-x_{j}\Vert^2}{\sigma}) K(xi,xj)=exp(−σ∥xi−xj∥2) |
| sigmoid核 | K ( x i , x j ) = t a n h ( β x i T x j + θ ) K(x_{i},x_{j}) =tanh(\beta x_{i}^Tx_{j}+\theta) K(xi,xj)=tanh(βxiTxj+θ) |
求解其中的 α i \alpha_{i} αi
为了求解 α i \alpha_{i} αi,人们发现了许多方法。例如 S M O SMO SMO算法,在西瓜书上有更为详细的讲解。
代码实现
code by young_monkeysun 2019
'''
SOM算法流程:
1,构造函数设置循环优化次数。
2.在(0~C)范围内初始化拉格朗日乘子a,位移b,
外循环:交替遍历 整个样本集 和 遍历非边界样本集 选取违反KKT条件的a_i作为第一个变量
KTT条件:a_i = 0 ➡ y^i( W^T*x^i + b )>=1
a_i = C ➡y^i( W^T*x^i + b ) <= 1
0H时 ,a2_new = H
当L<=a2_new<=H时,a2_new = a2_new
当a2_new
import numpy
import random
import pandas
import matplotlib.pyplot as plt
#设置中文编码
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class SVM(object):
def __init__(self,iteration):
self.iteration = iteration
#拉格朗日乘子a未全部更新完成的预测模型,判断样本类别
def fxi(self,alphas,labels,datas,data_i,b):
ai_yi = numpy.multiply(alphas,labels) #拉格朗日乘子中每个α与数据集的对应标签相乘
w = numpy.dot(ai_yi,datas)
return numpy.dot(w,data_i)+b
#交替从 整个样本集 和 遍历非边界样本集 选取违反KKT条件的a_i作为第一个变量
#flag=1表示从样本集中选取,flag=0表示从非边界样本集中选取
def select_a1(self,flag,alphas,labels,datas,b):
#从样本集中选取
if flag==1:
locate = -1 #标志位,当返回值为-1时已经全部满足kkt条件
for i in range(len(alphas)):
kkt = labels[i]*self.fxi(alphas,labels,datas,datas[i],b)
if alphas[i]==0 and kkt<1 or kkt>1 or alphas[i]>0 and kkt!=1:
locate = i
flag = 0
break
#从非边界样本集中选取
else:
locate = -1
for i in range(len(alphas)):
kkt = labels[i]*self.fxi(alphas,labels,datas,datas[i],b)
if alphas[i]>0 and kkt!=1:
locate = i
flag = 1
break
return locate ,flag
#选取与a1差距最大的a2
def select_a2(self,alphas,labels,datas,b,locate_1):
E1 = self.fxi(alphas,labels,datas,datas[locate_1],b) - labels[locate_1]
distance = 0
for i in range(len(alphas)):
if i != locate_1:
E2 = self.fxi(alphas,labels,datas,datas[i],b) - labels[i]
new_distance = abs(E1-E2)
if new_distance>distance:
distance = new_distance
locate_2 = i
return locate_2
#计算除固定的a1和a2的Σai*yi
def Sigma_ai_yi(self , alphas, labels , locate_1 , locate_2):
Sigma_ai_yi = 0
for i in range(len(alphas)):
if i != locate_1 and i != locate_2:
Sigma_ai_yi += alphas[i]*labels[i]
return Sigma_ai_yi
#选取完a1,a2后优化a1,a2
def update_a1_a2(self,alphas,labels,locate_1,locate_2,datas,b):
a1_old = alphas[locate_1]
a2_old = alphas[locate_2]
# if labels[locate_1] != labels[locate_2] :
# L = max( 0 , a2_old-a1_old )
# H = min( 0.6, 1+a2_old-a1_old )
# else:
# L = max(0 ,a2_old+a1_old -0.6 )
# H = min(0.6 , a2_old+a1_old )
#计算新a2
E1 = self.fxi(alphas,labels,datas,datas[locate_1],b) - labels[locate_1]
E2 = self.fxi(alphas,labels,datas,datas[locate_2],b) - labels[locate_2]
eta = numpy.dot(datas[locate_1],datas[locate_1].T)+numpy.dot(datas[locate_2],datas[locate_2].T) - 2*numpy.dot(datas[locate_1],datas[locate_2].T)
a2_new = a2_old +labels[locate_2]*(E1-E2)/eta
'''根据a2_new对a2_new进行修剪
当a2_new>H时 ,a2_new = H
当L<=a2_new<=H时,a2_new = a2_new
当a2_new
# if a2_new > H:
# a2_new = H
# if a2_new
# a2_new = L
#//针对a2修剪完成
#更新a1
a1_new = a1_old+labels[locate_1]*labels[locate_2]*(a2_old-a2_new)
'''更新b
当0
b1 = -E1-labels[locate_1]*numpy.dot(datas[locate_1],datas[locate_1])*(a1_new-a1_old)-labels[locate_2]*numpy.dot(datas[locate_2],datas[locate_1])*(a2_new-a2_old) +b
b2 = -E2-labels[locate_1]*numpy.dot(datas[locate_1],datas[locate_2])*(a1_new-a1_old)-labels[locate_2]*numpy.dot(datas[locate_2],datas[locate_2])*(a2_new-a2_old)+b
# if a1_new > 0 :
# b = b1
# elif a2_new > 0:
# b = b2
# else:
b = (b+b1+b2)/3
alphas[locate_1] = a1_new
alphas[locate_2] = a2_new
return b
def SMO(self,labels,datas):
#初始化拉格朗日乘子α和b
m = len(labels)
self.alphas = numpy.random.rand(1,m)[0]
self.b= 0
for itera in range(self.iteration):
'''选择a1,选择a2
'''
flag_a1 = 1
for i in range(m):
locate_1 , flag_a1 = self.select_a1(flag_a1,self.alphas,labels,datas,self.b)
#当找不到可以进行优化的α时,表示优化完成,终止所有循环
if locate_1 == -1:
break
#内循环选择a2
locate_2 = self.select_a2(self.alphas,labels,datas,self.b,locate_1)
#对a1,a2,b进行优化更新
self.b = self.update_a1_a2(self.alphas,labels,locate_1,locate_2,datas,self.b)
#以上优化更新迭代完成,之后计算W*
self.w = numpy.dot(numpy.multiply(self.alphas,labels),datas)
read_file = pandas.read_csv('testSet.csv')
labels= read_file.iloc[0:100,2].values
datas = read_file.iloc[0:100,[0,1]].values
# b是常量值, alphas是拉格朗日乘子
svm = SVM(200)
svm.SMO(labels,datas)
#计算超平面直线
y1 = -4
x1 = (-svm.b-svm.w[1]*y1)/svm.w[0]
y2 = 4
x2 = (-svm.b-svm.w[1]*y2)/svm.w[0]
# 画出样本数据集图像
for i in range(len(labels)):
if labels[i] > 0 :
plt.scatter(datas[i,0],datas[i,1],color = 'black',marker='o')
else:
plt.scatter(datas[i,0],datas[i,1],color = 'red',marker='x')
plt.plot([x1,x2],[y1,y2])
plt.xlabel('x轴')
plt.ylabel('y轴')
plt.title('训练样本图像')
plt.show()
总结
SVM算法远没有这么简单,SVM还分为硬间隔SVM、软间隔SVM、核技巧SVM等。现在只是知道了其基本原理,里面还有许多细节值得研究。在其他大神的博客中有更为详细全面完整的介绍。