Python实现K-Means聚类（案例：用户分类）

目录

K-Means聚类算法介绍

K-Means聚类算法基础原理

K-Means聚类算法实现流程

开始做一个简单的聚类

数据导入

数据探索 

开始聚类

查看输出结果

聚类质心

K-Means聚类算法的评估指标

真实标签已知

真实标签未知

实用案例：基于轮廓系数来选择最佳的n_clusters

绘制轮廓系数分布图

结果对比

优化方案选择

---

K-Means聚类算法介绍

K-Means又称为K均值聚类算法，属于聚类算法中的一种，而聚类算法在机器学习算法中属于无监督学习，在业务中常常会结合实际需求与业务逻辑理解来完成建模；

无监督学习：训练时只需要特征矩阵X，不需要标签；

K-Means聚类算法基础原理

K-Means聚类算法是聚类算法家族中的典型代表，同时也是最简单的算法，接下来为大家简单地介绍聚类算法基本原理：

将一组存在N个样本的特征矩阵X划分为K个无交集的簇，每一个簇中含有多个数据，每一个数据代表着一个样本，在同一个簇中的数据即被算法认为是同一类；

• N：假设为样本数量；
• K：假设为聚类簇的数量；
• 簇：类似于集合，也可以通俗地理解成一个小组，不同小组等于不同分类；

而一个簇中的所有数据的均值，被称为这个簇的质心，质心的维度与特征矩阵X的维度相同，如特征矩阵X是三维数据集，质心也就是一个三维的坐标，如此类推至更高维度；

K-Means聚类算法实现流程

步骤一：随机在N个样本中抽取K个作为初始的质心；

步骤二：开始遍历除开质心外的所有样本点，将其分配至距离它们最近的质心，每一个质心以及被分配至其下的样本点视为一个簇（或者说一个分类），这样便完成了一次聚类；

步骤三：对于每一个簇，重新计算簇内所有样本点的平均值，取结果为新的质心；

步骤四：比对旧的质心与新的质心是否再发生变化，若发生变化，按照新的质心从步骤二开始重复，若没发生变化，聚类完成；

关键要点：不断地为样本点寻找质心，然后更新质心，直至质心不再变化；

开始做一个简单的聚类

环境说明：本文实际案例中使用Jupyter环境下运行（安装与使用可自行百度）；

数据导入

做数据分析前，首先第一步是导入数据，可以利用pandas内的read_csv函数来导入数据；

首先，导入所需要用到的类，并使用read_csv函数导入案例数据：

import numpy as np
import pandas as pd

data = pd.read_csv(r'D:\Machine_learning\KMeans\client_data.csv')

# 使用pandas中的read_csv函数导入数据集后，默认格式为DataFrame

# 直接查看当前数据集长什么样子

data.head()

数据打开后会发现大概长这样：

	交易额	成交单量	最近交易时间
0	76584.92	294	64
1	94581.00	232	1
2	51037.60	133	1
3	43836.00	98	1
4	88032.00	95	2

# 若表头项为中文时，可能出现乱码情况，请自行百度解决，或直接修改为英文；

数据探索 

先探索数据类型：

# 探索数据类型
data.info()

# 输出结果：

RangeIndex: 8011 entries, 0 to 8010
Data columns (total 3 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   交易额     8011 non-null   float64
 1   成交单量    8011 non-null   int64  
 2   最近交易时间  8011 non-null   int64  
dtypes: float64(1), int64(2)
memory usage: 187.9 KB

• 共8011个数据样本，3个维度列（2个整数、1个浮点数），且无缺失数据；
• 数据背景：从三个维度获取所有用户交易180天内交易数据（数据获取、清洗规则在此不作详细说明）；
• 第一列：索引（read_csv函数导入数据时会自动生成索引，若数据集本身自带索引，可设置参数index_=0，代表数据集中第一列为索引）；
• 第二列：180天内交易额，浮点数；
• 第三列：180天内成交单量，整数；
• 第四列：最近成交订单的日期与当前日期差，整数（180内无数据按照180运算）；

 由于sklearn中K-Means聚类算法仅支持二维数组运算，所以要先将数据集转化为二维数组：

data = np.array(data,type(float))

# 查看数据集
data

——————————————————————————————————————————————————
# 输出结果：
array([[76584.92, 294.0, 64.0],
       [94581.0, 232.0, 1.0],
       [51037.6, 133.0, 1.0],
       ...,
       [0.0, 0.0, 180.0],
       [0.0, 0.0, 180.0],
       [0.0, 0.0, 180.0]], dtype=object)

 查看数组结构：

# 查看数组结构
data.shape

——————————————————————————————————————————————————
# 输出结果：
(8011, 3)

开始聚类

数据集导入完成后，现在调用sklearn完成简单的聚类：

from sklearn.cluster import KMeans

X = data

# 实例化K-Means算法模型，先使用5个簇尝试聚类
cluster = KMeans(n_clusters=5, random_state=0)

# 使用数据集X进行训练
cluster = cluster.fit(X)

# 调用属性labels_，查看聚类结果
cluster.labels_

——————————————————————————————————————————————————
# 输出结果：
array([4, 4, 1, ..., 0, 0, 0])

• 参数n_clusters：
  设定聚类的目标簇数量，本次聚类先用5个簇尝试；
• 参数random_state：
  设定随机数种子，若不设定则每次聚类时都会使用不同的随机质心；
• 接口fit（）：
  使用数据集对模型进行训练；
• 属性labels_：
  查看训练后，每一样本的预测分类结果；

查看输出结果

查看输出结果的数组结构：

# 查看预测结果的数据结构
cluster.labels_.shape

——————————————————————————————————————————————————
# 输出结果：
(8011,)

分类结果的数组结构为（8011,），刚好对应着8011个样本的预测分类结果；

再次确认目标分类结果只有5类，可以使用numpy中的unique（）函数实现：

# 查看数组中存在的类别（对一维数组去重）
np.unique(cluster.labels_)

————————————————————————————————————————
# 输出结果：
array([0, 1, 2, 3, 4])

输出结果0~4中分别代表着5个不同的分类；

查看预测结果中每一分类的数量：

# 查看每一分类结果的数量
pd.value_counts(cluster.labels_)

——————————————————————————————————————————
0    7068
2     688
4     198
1      38
3      19
dtype: int64

分类为0的数据占比较大（约88%），这部分数据数据实际行业应用中的长尾数据，这类用户对平台几乎没有任何价值贡献；

聚类质心

聚类质心代表每一个分类簇的中心，某种意义上讲，质心坐标可以代表着这一个簇的普遍特征，质心可以通过调用属性cluster_centers_来查看：

# 查看质心
cluster.cluster_centers_

——————————————————————————————————————————————————————————
# 输出结果：
array([[3.40713759e+02, 7.43350311e-01, 1.48025750e+02],
       [4.30125087e+04, 4.70000000e+01, 2.03947368e+01],
       [6.06497324e+03, 9.37354651e+00, 3.55159884e+01],
       [7.57037853e+04, 7.84736842e+01, 1.52631579e+01],
       [1.80933537e+04, 2.34040404e+01, 1.49444444e+01]])

输出结果中分别对应着0~4五种分类的普遍数据特征；

K-Means聚类算法的评估指标

当我们完成聚类建模后，怎么知道聚类的效果好不好，这时我们便需要「评估指标」来评价模型的优劣，并根据此来调整参数；

对于聚类算法的评估指标，从大方向上区分为两种：真实标签已知与真实标签未知；

真实标签已知

即我们对于每一个样本的标签Y都是已知的，但是这种情况在实际的业务中几乎是不存在的，若标签已知，使用分类算法（如随机森林、SVM等）在各个方面来说都会更加合适；

• 调整兰德系数：

在sklearn中的类为sklearn.metrics.adjusted_rand_score(y_true, y_pred)

y_true：代表测试集中一个样本的真实标签；

y_pred：使用测试集中样本调用预测接口的预测结果（上文中使用的cluster.labels_）；

调整兰德系数的取值在[-1,1]：数值越接近1越好，大于0时聚类效果较为优秀，小于0时代表簇内差异巨大甚至相互独立，模型几乎不可用；

由于案例数据集中真实标签是未知的，故不在此展示；

真实标签未知

即我们对每一个样本的标签Y都是未知的，我们事先不知道每一个样本是属于什么分类，这种情况才是符合我们实际业务中真实使用聚类算法的场景；

• 轮廓系数系数：

在sklearn中的类为：

返回轮廓系数的均值：sklearn.metrics.silhouette_score(X, y_pred)；

返回数据集中每个样本自身的轮廓系数：sklearn.metrics.silhouette_sample(X, y_pred)；

轮廓系数的取值在（-1,1）：

对于某一样本点来说，当值越接近1时就代表自身与所在的簇中其他样本越相似，并且与其他簇中的样本不相似，而当值越接近-1时则代表与上述内容相反；综述，轮廓系数越接近1越好，负数则表示聚类效果非常差；

那接下来看看轮廓系数在刚才的聚类中效果如何：

# 导入轮廓系数所需要的库
from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples

# 查看轮廓系数均值
silhouette_score(X,cluster.labels_)

——————————————————————————————————————————————————
# 输出结果
0.8398497410297728

——————————————————————————————————————————————————
# 查看每一样本轮廓系数
silhouette_samples(X,cluster.labels_)

——————————————————————————————————————————————————
# 输出结果
array([0.94301872, 0.94301872, 0.94301872, ..., 0.64706719, 0.60820687,
       0.58272791])

——————————————————————————————————————————————————
# 查看样本轮廓系数结果的数组结构
silhouette_samples(X,cluster.labels_).shape

——————————————————————————————————————————————————
# 输出结果
(8011,)

本次聚类的轮廓系数为0.84，表示聚类效果良好；

样本轮廓系数的数据结构可以看出：数组中每一个输出结果对应着每一个样本的轮廓系数，共8011个；

• 卡林斯基-哈拉巴斯指数：

sklearn中的类：sklearn.metrics.calinski_haabasz_score (X, y_pred)；

 卡林斯基-哈拉巴斯指数的数值无上限，且对于模型效果来说越高越好，而由于无上限的特性，导致只能用作对比，而无法快速知晓模型效果是否好；

可以看看轮廓系数在刚才的聚类中效果如何：

# 调用所需要的类
from sklearn.metrics import calinski_harabasz_score

calinski_harabasz_score(X,cluster.labels_)

———————————————————————————————————————————————————————
# 输出结果
31777.971149699857

输出的结果为31778，那究竟效果如何？因为没有对照组，所以无法得知，如果有兴趣的小伙伴可以在调整参数的时候使用对照组试试效果；

实用案例：基于轮廓系数来选择最佳的n_clusters

需要绘制轮廓系数分布图，先导入所需用到的库：

import matplotlib.pyplot as plt
import matplotlib.cm as cm

绘制轮廓系数分布图

使用for循环分别对2~8个簇的情况画出轮廓系数分布图：

for n_clusters in [2,3,4,5,6,7,8]:
    n_clusters = n_clusters
    # 设置画布
    fig, ax1 = plt.subplots(1)
    # 设置画布尺寸
    fig.set_size_inches(18, 7)
    # 设置画布X轴
    ax1.set_xlim([-0.1, 1])
    # 设置画布Y轴：X.shape[0]代表着柱状的宽度，(n_clusters + 1) * 10代表着柱与柱之间的间隔
    ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
    # 模型实例化
    clusterer = KMeans(n_clusters=n_clusters, random_state=100)
    # 开始训练模型
    clusterer = clusterer.fit(X)
    # 提取训练结果中的预测标签
    cluster_labels = clusterer.labels_
    # 提取训练结果中的轮廓系数均值
    silhouette_avg = silhouette_score(X, cluster_labels)
    # 打印出当前的簇数与轮廓系数均值
    print("簇数为", n_clusters,
          "，轮廓系数均值为", silhouette_avg)
    # 提取每一个样本的轮廓系数
    sample_silhouette_values = silhouette_samples(X, cluster_labels)
    # 设置Y轴的起始坐标
    y_lower = 10
    # 添加一个循环，把每一个样本的轮廓系数画在图中
    for i in range(n_clusters):
        # 提取第i个簇下的所有样本轮廓系数
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
        # 对样本的轮廓系数进行排序（降序）
        ith_cluster_silhouette_values.sort()
        # 设置当前簇的柱状宽度（使用样本数量）以便于设置下一个簇的起始坐标
        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        # 设置Y轴第i个簇的起始坐标
        y_upper = y_lower + size_cluster_i
        # 设置颜色
        color = cm.nipy_spectral(float(i)/n_clusters)
        # 画图
        ax1.fill_betweenx(np.arange(y_lower, y_upper)
                         ,ith_cluster_silhouette_values
                         ,facecolor=color
                         ,alpha=0.7
                         )
        ax1.text(-0.05
                 , y_lower + 0.5 * size_cluster_i
                 , str(i))
        y_lower = y_upper + 10
    # 设置图的标题
    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")
    # 添加轮廓系数均值线，使用虚线
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
    ax1.set_yticks([])
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
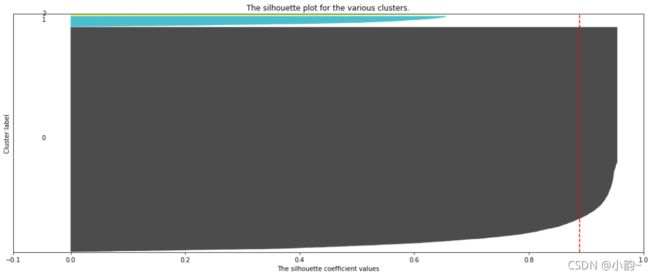
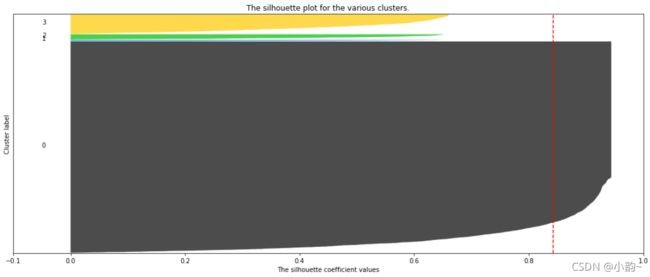
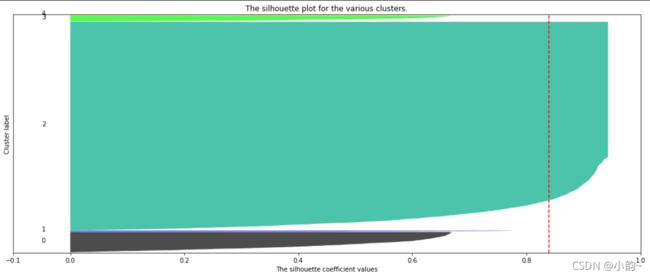
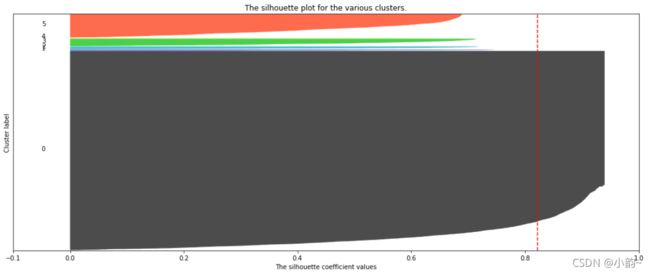
    plt.show()

结果对比

输出结果：

• 簇数为 2 ，轮廓系数均值为 0.9348704011138467：

• 簇数为 3 ，轮廓系数均值为 0.8889120986545176：

•  簇数为 4 ，轮廓系数均值为 0.8432045328349393：

• 簇数为 5 ，轮廓系数均值为 0.8397653971050274：

• 簇数为 6 ，轮廓系数均值为 0.8217141668609508：

• 簇数为 7 ，轮廓系数均值为 0.7995236853252528：

• 簇数为 8 ，轮廓系数均值为 0.7995236853252528：

 从本次的输出结果中可知，当簇数量为2时，会存在最大的轮廓系数均值，是否簇数量为2就是最佳的参数呢？

答案必须是否定的，我们可以通过轮廓系数分部图看到，基本上每一个图内都会有一片面积很大的块，这就是长尾数据带来的，因为他们基本都集中在一个点上，所以导致整体轮廓系数均值“被平均”得很大，这样的状况也是很多实际业务数据中常常会碰到的；

优化方案选择

既然由于长尾数据对轮廓系数带来较大偏差，那咱们的思路可以把长尾数据剔除掉，仅计算非长尾数据（数据分析需要在不同的具体场景下有不同的思路，以下仅是一种思路举例）；

• 当簇数量为3时：

# 实例化，训练模型
n_clusters = 3
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)

# 查看训练结果
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
0    7599
1     362
2      50
dtype: int64

长尾数据所在的簇为0，计算非长尾数据的轮廓系数均值：

cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 0]))

——————————————————————————————————————————————————————————————————————————————
# 输出结果
0.4909204497858037

• 当簇数量为4时：

# 实例化，训练，并查看结果分布
n_clusters = 4
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
0    7125
3     663
2     179
1      44
dtype: int64

————————————————————————————————————————————————————————————
# 计算非长尾数据的轮廓系数均值
cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 0]))

————————————————————————————————————————————————————————————
# 输出结果
0.4766824917258095

•  当簇数量为5时：

# 实例化，训练，并查看结果分布
n_clusters = 5
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
2    7065
0     691
3     198
1      38
4      19
dtype: int64

————————————————————————————————————————————————————————————
# 计算非长尾数据的轮廓系数均值
cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 2]))

————————————————————————————————————————————————————————————
# 输出结果
0.49228555254491085

• 当簇数量为6时：

# 实例化，训练，并查看结果分布
n_clusters = 6
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
0    6806
5     799
3     252
2      99
1      36
4      19
dtype: int64

————————————————————————————————————————————————————————————
# 计算非长尾数据的轮廓系数均值
cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 0]))

————————————————————————————————————————————————————————————
# 输出结果
0.5043196493336838

• 当簇数量为7时：

# 实例化，训练，并查看结果分布
n_clusters = 7
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
0    6374
5     931
6     387
2     188
1      76
4      36
3      19
dtype: int64

————————————————————————————————————————————————————————————
# 计算非长尾数据的轮廓系数均值
cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 0]))

————————————————————————————————————————————————————————————
# 输出结果
0.501667625921486

• 当簇数量为8时：

# 实例化，训练，并查看结果分布
n_clusters = 8
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)
pd.value_counts(clusterer.labels_)

————————————————————————————————————————————————————————————
# 输出结果
0    6411
5     927
4     372
2     172
6      74
1      32
7      13
3      10
dtype: int64

————————————————————————————————————————————————————————————
# 计算非长尾数据的轮廓系数均值
cluster_labels = clusterer.labels_
print(np.average(silhouette_samples(X, cluster_labels)[cluster_labels != 0]))

————————————————————————————————————————————————————————————
# 输出结果
0.4974116370311323

对比上述结果，当n_clusters=6时，轮廓系数均值存在最大值0.5043；

这时查看质心的坐标：

# 设置参数n_clusters=6再次训练模型
n_clusters = 6
clusterer = KMeans(n_clusters=n_clusters, random_state=100)
clusterer = clusterer.fit(X)

# 使用属性cluster_centers_查看质心坐标
clusterer.cluster_centers_

——————————————————————————————————————————————————————————————
# 输出结果
array([[2.50559675e+02, 5.95944755e-01, 1.51620923e+02],
       [4.36372269e+04, 4.83333333e+01, 2.06111111e+01],
       [2.23257222e+04, 2.73232323e+01, 1.72020202e+01],
       [1.15493973e+04, 1.65515873e+01, 1.95833333e+01],
       [7.57037853e+04, 7.84736842e+01, 1.52631579e+01],
       [4.25642288e+03, 6.82227785e+00, 4.39336671e+01]])

——————————————————————————————————————————————————————————————
# 查看聚类结果分布
pd.value_counts(clusterer.labels_)

——————————————————————————————————————————————————————————————
# 输出结果
0    6806
5     799
3     252
2      99
1      36
4      19
dtype: int64

——————————————————————————————————————————————————————————————
# 聚类结果分布以百分比形式显示
pd.value_counts(clusterer.labels_,normalize=True)

——————————————————————————————————————————————————————————————
# 输出结果
0    0.849582
5    0.099738
3    0.031457
2    0.012358
1    0.004494
4    0.002372
dtype: float64

从结果可得（数据结果为科学计数法），6个类别客户的画像特征分别对应着：

• 分类0——6806位——占比85%：
  交易额：251元，平均单量：0.6单，最近交易时间：152天前；
• 分类1——36位——占比0.4%：
  交易额：43637元，平均单量：48单，最近交易时间：21天前；
• 分类2——99位——占比1.2%：
  交易额：22325元，平均单量：27单，最近交易时间：17天前；
• 分类3——252位——占比3.1%：
  交易额：11549元，平均单量：17单，最近交易时间：20天前；
• 分类4——19位——占比0.2%：
  交易额：75703元，平均单量：78单，最近交易时间：15天前；
• 分类5——799位——占比10%：
  交易额：4256元，平均单量：7单，最近交易时间：44天前；