机器学习算法--python实现常用的聚类算法—k-均值算法(基于原型聚类)+SSE+轮廓图
基于原型的聚类方法意味着每个集群代表一个原型,可以是有类似连续性特征点的重心,或者是在分类特征最具代表性或最频繁出现的中心。
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
# 生成数据集
# 用于创建多类单标签数据集的函数,它为每个类分配一个或多个正态分布的点集
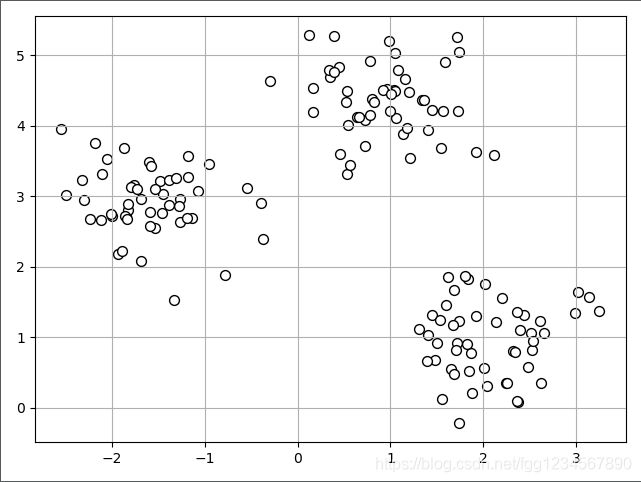
X, y = make_blobs(n_samples=150, # 待生成的样本的总数
n_features=2, # 每个样本的特征数
centers=3, # 要生成的样本中心(类别)数,或者是确定的中心点
cluster_std=0.5, # 每个类别的标准差
shuffle=True, # 是否将样本打乱
random_state=0) # 随机生成器的种子
km = KMeans(n_clusters=3,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
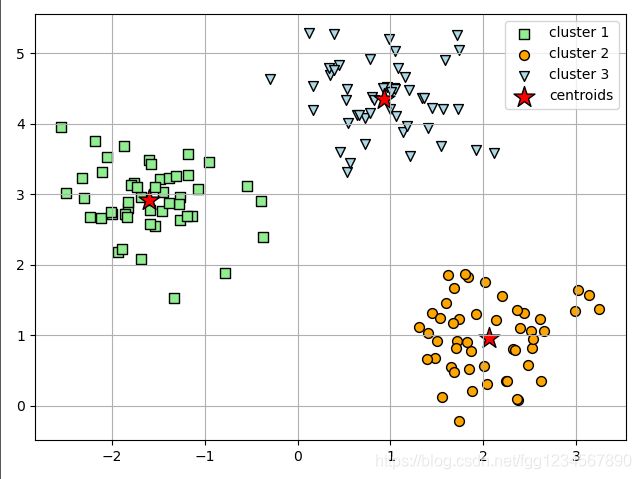
plt.scatter(X[y_km == 0, 0],
X[y_km == 0, 1],
s=50,
c='lightgreen',
edgecolor='black',
marker='s',
label='cluster 1')
plt.scatter(X[y_km == 1, 0],
X[y_km == 1, 1],
s=50,
c='orange',
edgecolor='black',
marker='o',
label='cluster 2')
plt.scatter(X[y_km == 2, 0],
X[y_km == 2, 1],
s=50, c='lightblue',
marker='v', edgecolor='black',
label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', label='centroids')
plt.legend()
plt.grid()
plt.tight_layout()
#plt.savefig('images/11_05.png', dpi=300)
plt.show()
# SSE:群内SSE(失真)来比较不同k-均值聚类性能
print('Distortion: %.2f' % km.inertia_)
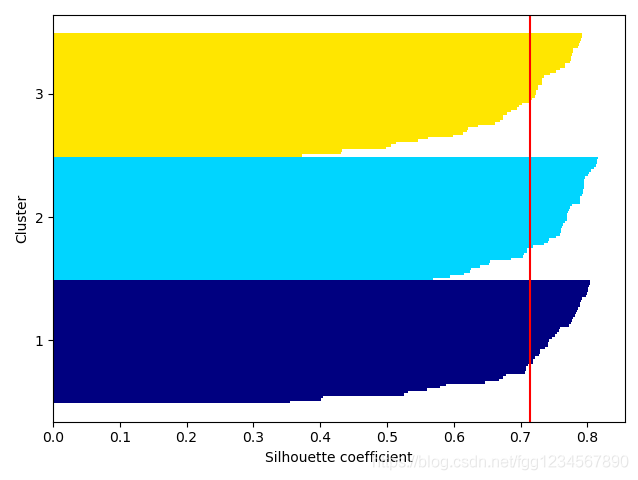
# 轮廓图
# 现实世界的问题通常没有条件把数据可视化在二维散点图上。
# 因为通常模型在更高维的数据集上工作。通常将创建轮廓图来评价结果
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,
edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="-")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
# plt.savefig('images/11_06.png', dpi=300)
plt.show()
运行结果:
Distortion: 72.48
备注:k-均值方法非常擅长识别球形集群,其缺点是必须指定集群数k,所以它是个先验方法