python_sklearn机器学习算法系列之K-Means(硬聚类算法)

          本文主要目的是通过一段及其简单的小程序来快速学习python 中sklearn的K-Means这一函数的基本操作和使用，注意不是用python纯粹从头到尾自己构建K-Means，既然sklearn提供了现成的我们直接拿来用就可以了，当然K-Means原理还是十分重要，这里简单说一下实现这一算法的过程：

1)从N个文档随机选取K个文档作为质心

2)对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类

3)重新计算已经得到的各个类的质心

4)迭代2~3步直至新的质心与原质心相等或小于指定阈值，算法结束

详细可以参考https://baike.so.com/doc/6953641-7176056.html

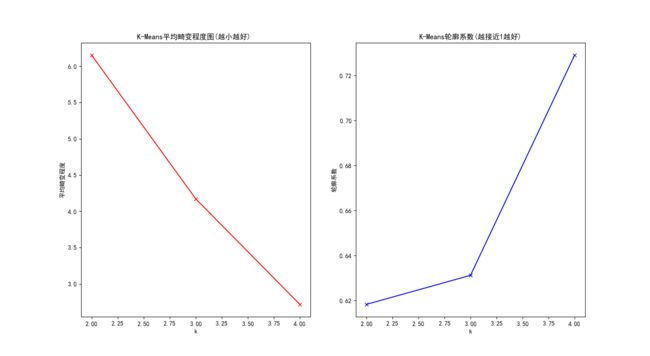
在介绍代码之前先来看两个概念：平均畸变程度和轮廓系数

通过平均畸变程度可以确定一个范围内(人为给定)的最佳类簇的数量即K值,通过轮廓系数(Silhouette Coefficient)评价聚类算法的性能

每个类的畸变程度简单来说其实等于该类重心与其内部成员位置距离的平方和，显而易见该值越小说明该类中的样本越紧凑的聚集在一起，

平均畸变程度越小说明整体来说分类的效果越好了对吧，所以这个概念还是比较好理解的，也可以从下面的代码中清楚的看到这一概念的具体含义。

关于轮廓系数有点复杂，它由两个因数通过决定：簇内不相似度和簇间不相似度

簇内不相似度定义为样本n到同簇其他样本的平均距离，记为dist1_n

设样本n到其他某簇C(i) 的所有样本的平均距离dis_n-C(i)则簇间不相似度定义为dist2_n=min{dis_n-C(1), dis_n-C(2), ...,dis_n-C(k)}

则轮廓系数s为（图片旋转一下看）：

s接近1，则说明样本n聚类合理；

s接近-1，则说明样本n更应该分类到另外的簇；

若s 近似为0，则说明样本n在两个簇的边界上。

本程序源数据用的是一部分城市的经纬度即city.txt

上海上海,121.48,31.22  
上海嘉定,121.24,31.4  
上海宝山,121.48,31.41  
上海川沙,121.7,31.19  
上海南汇,121.76,31.05  
上海奉贤,121.46,30.92  
上海松江,121.24,31  
云南昆明,102.73,25.04  
云南富民,102.48,25.21  
云南晋宁,102.58,24.68  
云南呈贡,102.79,24.9  
云南安宁,102.44,24.95  
云南昭通,103.7,29.32  
云南永善,103.63,28.22  
云南大姚,101.34,25.73  
云南永仁,101.7,26.07  
云南禄劝,102.45,25.58  
云南牟定,101.58,25.32  
云南双柏,101.67,24.68  
云南姚安,101.24,25.4  
云南下关,100.24,25.45  
云南剑川,99.88,26.53  
云南洱源,99.94,26.1  
云南宾川,100.55,25.82  
云南弥渡,100.52,25.34  
云南永平,99.52,25.45  
云南鹤庆,100.18,26.55  
云南大理,100.19,25.69  
云南漾濞,99.98,25.68  
北京北京,116.46,39.92  
北京平谷,117.1,40.13  
北京密云,116.85,40.37  
北京顺义,116.65,40.13  
北京通县,116.67,39.92  
北京怀柔,116.62,40.32  
北京大兴,116.33,39.73  
北京房山,115.98,39.72    
吉林长春,125.35,43.88  
吉林吉林,126.57,43.87  
吉林农安,125.15,44.45  
吉林德惠,125.68,44.52  
吉林榆树,126.55,44.83  
吉林九台,126.83,44.15  
吉林双阳,125.68,43.53  
吉林永吉,126.57,43.87  
吉林舒兰,126.97,44.4  
吉林蛟河,127.33,43.75  
吉林桦甸,126.72,42.97  
吉林磐石,126.03,42.93  
吉林延吉,129.52,42.93  
吉林汪清,129.75,43.32  
吉林珲春,130.35,42.85  
吉林大安,124.18,45.5  
吉林扶余,124.82,45.2  
吉林乾安,124.02,45  
吉林长岭,123.97,44.3  
吉林通榆,123.13,44.82  
吉林洮安,122.75,45.35   
四川成都,104.06,30.67  
四川金堂,104.32,30.88  
四川双流,104.94,30.57  
四川蒲江,103.29,30.2  
四川郫县,103.86,30.8  
四川新都,104.13,30.82  
四川来易,102.15,26.9  
四川盐边,101.56,26.9  
天津天津,117.2,39.13  
天津宁河,117.83,39.33  
天津静海,116.92,38.93  
天津蓟县,117.4,40.05  
天津宝坻,117.3,39.75  
天津武清,117.05,39.4  
宁夏回族自治区银川,106.27,38.47  
宁夏回族自治区永宁,106.24,38.28  
宁夏回族自治区贺兰,106.35,38.55  
宁夏回族自治区石嘴山,106.39,39.04  
宁夏回族自治区平罗,106.54,38.91  
宁夏回族自治区陶乐,106.69,38.82  
宁夏回族自治区吴忠,106.21,37.99  
宁夏回族自治区同心,105.94,36.97  
宁夏回族自治区灵武,106.34,38.1
安徽郎溪,119.17,31.14  
安徽广德,119.41,30.89  
安徽泾县,118.41,30.68  
安徽南陵,118.32,30.91  
安徽繁昌,118.21,31.07  
安徽宁国,118.95,30.62  
安徽青阳,117.84,30.64  
安徽屯溪,118.31,29.72  
安徽休宁,118.19,29.81  
安徽旌得,118.53,30.28  
安徽绩溪,118.57,30.07  
安徽歙县,118.44,29.88  

好了前期工作介绍完毕，终于可以看程序了

其中，模块一是平均畸变程度和轮廓系数； 模块二是预测效果

我在这里将两模块都注释掉了，读者可以分别运行

代码：

#K-Means   
import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans
from sklearn.externals import joblib     #模块二
import pandas as pd
import matplotlib as mpl
from scipy.spatial.distance import cdist #模块一
from sklearn import metrics              #模块一

#从磁盘读取城市经纬度数据  
X = []  
f = open('city.txt')  
for v in f:
    X.append([float(v.split(',')[1]),float(v.split(',')[2])])
f.close()

#转换成numpy array,形如:[[1.2 , 3.2],[2.3 , 6.3 ],[1.0 , 2.3]]，转化前X是一个列表
X = np.array(X)

mpl.rcParams['font.sans-serif'] = [u'SimHei']            #绘图时用来正常显示中文标签    
mpl.rcParams['axes.unicode_minus'] = False               #绘图时用来正常显示负号


'''
#模块一：
#通过平均畸变程度来确定类簇的数量,通过轮廓系数(Silhouette Coefficient)评价聚类算法(具体来自https://blog.csdn.net/wangxiaopeng0329/article/details/53542606)
#d=cdist(X,Y,'euclidean')#假设X有M个元素，Y有N个元素，最终会生成M行N列的array，用来计算X、Y中每个相对元素之间的欧拉距离
#numpy.min(d,axis=1) #如果d为m行n列，axis=0时会输出每一列的最小值，axis=1会输出每一行最小值
n_clusters = range(2,5) #假设分别在2,3,4中选取一个最合适的n_clusters
meandistortions=[]
metrics_silhouette=[]
for k in n_clusters:
    clf=KMeans(n_clusters=k)
    cls = clf.fit(X)
    meandistortions.append(sum(np.min(cdist(X,clf.cluster_centers_,'euclidean'),axis=1))/X.shape[0])#平均畸变程度值，越小越好
    metrics_silhouette.append(metrics.silhouette_score(X,clf.labels_,metric='euclidean'))           #轮廓系数,越接近1越好   
#平均畸变程度图   
plt.subplot(121)
plt.plot(n_clusters,meandistortions,'rx-')
plt.xlabel('k')
plt.ylabel('平均畸变程度')
plt.title('K-Means平均畸变程度图(越小越好) ')
#轮廓系数图
plt.subplot(122)
plt.plot(n_clusters,metrics_silhouette,'bx-')
plt.ylabel('轮廓系数')
plt.xlabel('k')
plt.title('K-Means轮廓系数(越接近1越好)')
#显示
plt.show()

'''



'''   

#模块二：
#核心代码:现在把数据和对应的分类放入聚类函数中进行聚类
#其中n_clusters 需要聚成几类，init代表初始点怎么找，max_iter代表迭代次数， n_jobs用的cpu，precompute_distances预先需不需要计算距离
n_clusters=4
clf=KMeans(n_clusters=n_clusters)
cls = clf.fit(X)

#聚类结果的显示,其中用clf和cls均可
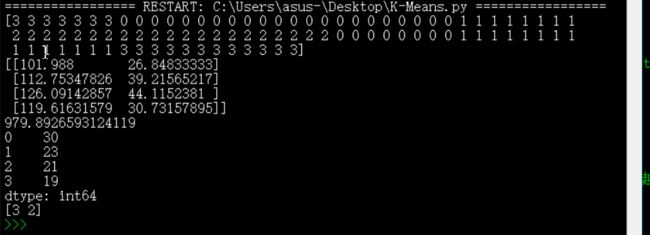
print(cls.labels_)                         #显示每个样本所属的簇
print(clf.cluster_centers_)                #4个中心点的坐标
print(clf.inertia_)                        #用来评估簇的个数是否合适，代表所有点到各自中心的距离和，距离越小说明簇分的越好，选取临界点的簇个数
r1 = pd.Series(cls.labels_).value_counts()
print(r1)                                  #统计每个类别下样本个数

#用聚类的学习结果去预测
X1=[[121.35,26.41],[123.5,45.35]]
print(clf.predict(X1))

#保存模型，加载模型(加载后是类别标签)
joblib.dump(clf,'d:/test/km.txt')
clf = joblib.load('d:/test/km.txt')

#画图
markers = ['x','o','*','+']
colors=['b','r','y','g']
for i in range(n_clusters):
     members = cls.labels_ == i
     plt.scatter(X[members,0],X[members,1],s=60,marker=markers[i],c=colors[i],alpha=0.5)
plt.xlabel('经度')
plt.ylabel('纬度')
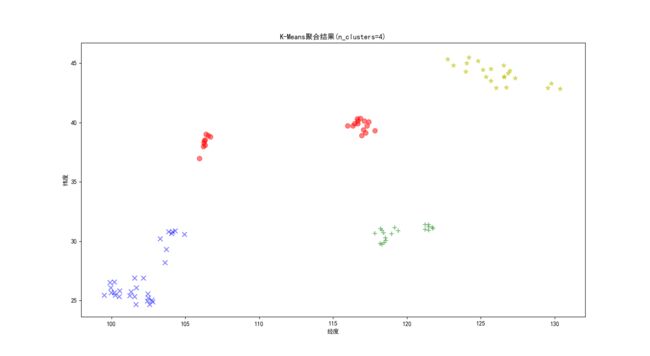
plt.title('K-Means聚合结果(n_clusters=4)')  
plt.show()

'''

模块一结果：

模块二结果：

更多算法可以参看博主其他文章，或者github：https://github.com/Mryangkaitong/python-Machine-learning

看到很多小伙伴私信，为了不迷路，欢迎关注笔者微信公众号：

​​​​​​​