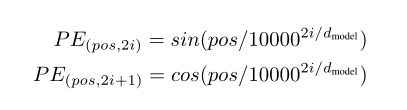attention is all you need

摘要

主流的序列转换模型都是基于复杂的循环或卷积神经网络，这个模型包含一个编码器和一个解码器。具有最好性能的模型是通过一个注意力机制，将编码和解码连接在一起。我们提出了一个新的简单网络结构——Transformer，其仅仅是基于注意力机制，完全不需要循环和卷积。在两个机器翻译任务上的实验表明，该模型具有更好的性能，同时可以进行并行化，并且需要更少的时间进行训练。在WMT 2014英语到德语翻译任务上，我们的模型达到了28.4的BLEU评分（（BiLingual Evaluation Understudy）双语互译质量评估辅助工具），获得了最好的结果。在WMT 2014英语到法语翻译任务上，我们的模型在8个GPU上训练3.5天后，所得到的单个模型获得了41.8BLEU分数，这个时间只是目前文献中记载的最好的模型训练成本的一小部分。我们在大型和有限的训练数据中，通过将其成功应用于英语句法解析，表明了Transformer可以很好地适用于其他任务。

 引言

        RNN,特别是LSTM,GRU 在序列建模和转换任务上，已经被确立为序列建模和转换问题（如语言建模和机器翻译[29，2，5]）中的最先进方法（state-of-the-art model，SOTA）。以后，许多研究都围绕循环语言模型和编码器-解码器体系结构进行。

  循环模型通常沿输入和输出序列的符号位置进行因子计算。在计算时将位置与步骤对齐，它们生成一系列隐藏状态ht，当前时刻隐藏态ht作为上一时刻隐藏状态ht−1和时刻 t输入的函数。这种内部的固有顺阻碍了训练样本的并行化，在序列较长时，这个问题变得更加严重，因为内存的限制限制了样本之间的批处理。最近的工作通过分解技巧（ factorization tricks）【18】和条件计算（conditional computation）【26】在计算效率方面取得了显著的提高，同时也提高了后者的模型性能。然而，顺序计算的基本约束仍然存在。

  在各种各样的任务中，注意力机制已经成为各种引人注目的序列模型和转换模型中组成部分，它允许对依赖关系建模，而不需要考虑它们在输入或输出序列中的距离。然而，在除少数情况外的所有情况下[22]，这种注意机制都与一个循环网络结合使用。

  在这项工作中，我们提出了Transformer，这是一种避免使用循环的模型架构，完全依赖于注意机制来绘制输入和输出之间的全局依赖关系。Transformer允许更多的并行化，使用8个P100 gpu训练了12小时，在翻译质量上就可以达到一个新的SOTA。

背景 

   减少顺序计算的目标也构成了Extended Neural GPU [20],ByteNet[15],和ConvS2S[8]的基础，所有这些都使用卷积神经网络作为基本构建块，并行计算所有输入和输出位置的隐藏表示。在这些模型中，关联来自两个任意输入或输出位置的数据所需的操作数，随着位置之间距离而增长，对于ConvS2S呈线性，对于ByteNet呈对数。这使得学习较远位置之间数据的依赖性变得更加困难。在Transformer中，这被减少到常数级的操作次数，尽管由于平均注意力加权位置而导致有效分辨率降低，如第3.2节所述，我们用多头注意力抵消这种影响。

  Self-attention，有时称为intra-attention，它将一个序列的不同位置联系起来，以计算序列的表示。Self-attention已经成功地用于各种任务，包括阅读理解、摘要概括、文本蕴涵和学习任务独立的句子表示。

  端到端的记忆网络使用循环attention机制替代序列对齐的循环，已经被证明在简单的语言问答和语言建模任务中表现良好。

  然而，据我们所知，Transformer是第一个完全依赖于self-attetion来计算其输入和输出表示而不使用序列对齐的RNN或卷积的转换模型，在下面的章节中，我们将描述由self-attention驱动的Transformer，并讨论它相对于[14,15]和[8]等模型的优势。

模型架构

         大多数神经序列转换模型都具有编码器-解码器结构。这里，编码器将字符表示的输入序列(x1,…,xn)映射到连续表示序列 z = (z1,…,zn)。在给定 z 的条件下，解码器以一次生成一个字符的方式生成输出序列( y 1 , . . . , y m ) 。在每个步骤中，模型都是自动回归的，在生成下一个字符时，将上一时刻生成的字符作为附加输入。

   Transformer遵循这个总体架构，使用堆叠的self-attention层和逐点全连接层，分别用于encoder和decoder，如图1的左半部分和右半部分所示。

①输入自然语言序列： Why do we work?
② 编码器输出的隐藏层是Why do we work的一种数学表示，类似于提取了每一个词的信息，然后汇总，转换成了这句话的数学向量。
③输入到解码器 ，输入符号到解码器 ，就会得到第一个字“为” 。
④将得到的第一个字“为”落下来再输入到解码器 ，得到第二个字“什” 。
⑤将得到的第二个字落下来输入，得到“么”，重复，直到解码器输出。 翻译完成 。

编码器栈和解码器栈

编码器：由N=6个相同层的layer堆栈组成。每层有两个子层。 第一个子层是multi-head self-attention，第二个子层是简单的、各位置独立的全连接层。我们在两个子层外面都使用了残差连接(residual connection)，然后进行层归一化（layer normalization）。也就是说，每个子层的输出是LayerNorm(x + Sublayer(x))，其中Sublayer(x)是当前子层的输出。为了提高这些残差连接，模型中的所有子层以及嵌入层产生的输出维度 dmodel=512。

解码器：也由N(N=6)个完全相同的layer堆叠而成.除了每个编码器层中的两个子层之外，解码器还插入第三个子层，该子层对编码器堆栈的输出执行multi-head attention操作，与encoder相似，我们在每个子层的后面使用了残差连接，之后采用了layer normalization。我们修改解码器堆栈中的self-attention子层以防止引入当前时刻的信息添加到后续时刻输入中。这种掩码与偏移一个位置的输出embedding相结合， 确保对第i 个位置的预测 只能依赖小于i的已知输出。

注意力机制

      attention函数可以被描述为将query和一组key-value对，映射到输出。其中query、key、value和输出都是向量。输出被计算为value的加权求和，其中分配给每个value的权重由query与对应key的兼容性函数计算。

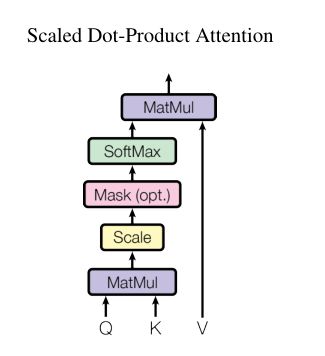
缩放点积注意力

我们将特殊的attention称为“缩放点积Attention”。输入由维度为 dk的query和key以及维度为dv的value组成。我们用所有key计算query的点积，然后将每个点积结果除以根号dk ，并应用softmax函数来获得value的权重。

缩放点注意力

         在实验中，我们同时在一组query上计算attention函数，将它们打包在一起形成矩阵Q。key和value也一起打包成矩阵K和V. 我们计算输出矩阵为：

         两个最常用的attention函数是加法attention和点积（乘法）attention。除了缩放因子 1/根号dk之外，点积attention与我们的算法相同。加法attention使用具有单个隐藏层的前馈网络来计算兼容性功能。虽然两者在理论上的复杂性相似，但在实践中，点积attention更快，更节省空间，因为它可以使用高度优化的矩阵乘法来实现。

       当dk的值比较小的时候，这两个机制的性能相差相近，当dk比较大时，加法attention比不带缩放的点积attention性能好。我们认为，对于很大的dk值，点积大幅度增长，将softmax函数推向具有极小梯度的区域。为了抵消这种影响，我们缩小点积1/根号dk倍。

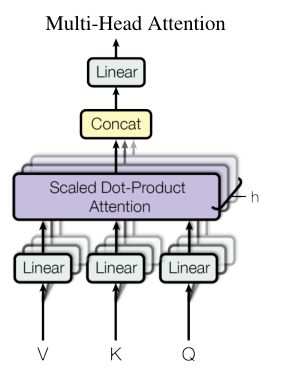
多头注意力

相比于用dmodel维的query、key和value执行单个attention函数，发现用不同的学习线性映射将query、key和value分别线性映射到dk、dk和dv维h次，效果更好。 基于每个映射版本的query、key和value，我们并行执行attention函数，产生dv 维输出值。 将它们拼接起来再次映射，产生最终值，如图所示2。

多头注意力

      Multi-head attention允许模型的不同表示子空间共同关注不同位置的信息。如果只有一个attention head，它的平均值会抑制这个信息。

 其中，映射为参数矩阵：

 在这项工作中，我们采用h=8 个并行attention层或head。对每个head，我们使用dk=dv=dmodel / h=64。由于每个head的大小减小，总的计算成本与具有全部维度的单个head attention相似。

注意力在模型中的应用

Transformer中用3种不同的方式使用multi-head attention：

①在“编码器—解码器attention”层，query来自前一个解码器层，key和value来自编码器的输出。这允许解码器中的每个位置能注意到输入序列中的所有位置。这模仿Seq2Seq模型中典型的编器—解码器的attention机制。
②编码器包含self-attention层。 在self-attention层中，所有的key、value和query来自相同的位置，即是编码器中前一层的输出。 编码器中的每个位置都可以关注编码器上一层的所有位置。
③类似地，解码器中的self-attention层允许解码器中的每个位置都参与解码器中直到并包括该位置的所有位置。为了保持解码器的自回归特性，需要防止解码器中的信息向左流动。我们在scaled dot-product attention的内部 ，通过屏蔽softmax输入中所有的非法连接值（设置为 −∞）实现了这一点。

基于位置的前馈神经网络

除了attention子层之外，我们的编码器和解码器中的每个层都包含一个 完全连接的前馈网络，该前馈网络单独且相同地应用于每个位置。 它包括两个线性变换，之间有一个ReLU激活。 

尽管线性变换在不同位置上是相同的，但它们在层与层之间使用不同的参数。它的另一种描述方式是两个内核大小为1的卷积。输入和输出的维度为dmodel = 512，内部层的维度为dff = 2048。

嵌入和Softmax

与其他序列转换模型类似，我们使用学习到的嵌入将输入词符和输出词符转换为维度为dmodel的向量。我们还使用普通的线性变换和softmax函数将解码器输出转换为预测的下一个词符的概率。在我们的模型中，两个嵌入层之间和pre-softmax线性变换共享相同的权重矩阵。在嵌入层中，我们将这些权重乘以根号dmodel。

位置编码

       由于我们的模型不包含循环和卷积，为了让模型利用序列的顺序，我们必须加入序列中关于词符相对或者绝对位置的一些信息。为此，我们将“位置编码”添加到编码器和解码器堆栈底部的输入嵌入中。位置编码和嵌入的维度dmodel相同，所以它们俩可以相加。有多种位置编码可以选择，例如通过学习得到的位置编码和固定的位置编码。

不同层类型的最大路径长度、每层复杂度和最小顺序操作数。n是序列长度，d是表示维数，k是卷积的核大小，r是受限自注意力中邻域的大小。 

 在这项工作中，我们使用不同频率的正弦和余弦函数:

                        

      其中pos 是位置，i 是维度。也就是说，位置编码的每个维度对应于一个正弦曲线。这些波长形成一个几何级数，从2π 到10000⋅2π。我们选择这个函数是因为我们假设它允许模型很容易学习相对位置，因为对任意固定偏移k, PEpos+k可以表示为PEpos的线性函数。

  我们还尝试使用预先学习的positional embeddings[9]来代替正弦波，发现这两个版本产生几乎相同的结果（参见表3行(E)）。我们选择了正弦曲线，是因为它允许模型扩展到比训练中遇到的序列长度更长的序列。

为什么选择selt-attention

本节，我们比较self-attention与循环层和卷积层的各个方面，它们通常用于映射变长的符号序列表示(x1,…,xn) 到另一个等长的序列(z1,…,zn)，其中xi,zi∈ ℝd，例如一个典型的序列转换编码器或解码器中的隐藏层。我们使用self-attention是考虑到解决三个问题。

       ①是每层计算的总复杂度。②是可以并行的计算，以所需的最小顺序操作的数量来衡量。

  ③是网络中长距离依赖之间的路径长度。学习长距离依赖性是许多序列转换任务中的关键挑战。影响学习这种依赖性能力的一个关键因素是前向和后向信号必须在网络中传播的路径长度。输入和输出序列中任意位置组合之间的这些路径越短，学习远距离依赖性就越容易。因此，我们还比较了由不同图层类型组成的网络中任意两个输入和输出位置之间的最大路径长度。

不同层类型的最大路径长度、每层复杂度和最小顺序操作数。n是序列长度，d是表示维数，k是卷积的核大小，r是受限自注意力中邻域的大小。 

       如表1所示，self-attention层用常数次(O(1))的操作连接所有位置，而循环层需要O(n) 顺序操作。在计算复杂性方面，当序列长度n 小于表示维度d 时，self-attention层比循环层快，这是机器翻译中最先进的模型最常见情况，例如word-piece表示法和byte-pair表示法。为了提高涉及很长序列的任务的计算性能，可以仅在以输出位置为中心，半径为r的的领域内使用self-attention。 这会将最大路径长度增加到O(n ∕ r)。我们计划在未来的工作中进一步调查这种方法。

         核宽度为k < n的单层卷积不会连接每一对输入和输出的位置。要这么做，在邻近核的情况下需要O(n∕k) 个卷积层，在扩展卷积的情况下需要O(logk(n)) 个层，它们增加了网络中任意两个位置之间的最长路径的长度。卷积层通常比循环层更昂贵，与因子k有关。然而，可分卷积大幅减少复杂度到O(k ⋅n⋅d + n⋅d2)。然而，即使k = n，一个可分卷积的复杂度等同于self-attention层和point-wise前向层的组合，即我们的模型采用的方法。

  间接的好处是self-attention可以产生更可解释的模型。我们从我们的模型中研究attention的分布，并在附录中展示和讨论示例。每个attention head不仅清楚地学习到执行不同的任务，许多似乎展现与句子的句法和语义结构的行为。