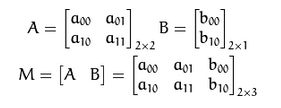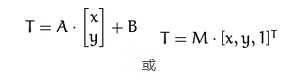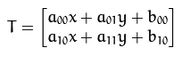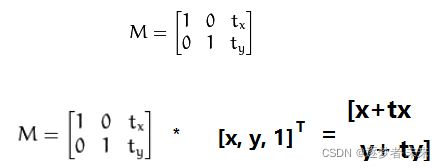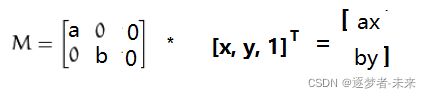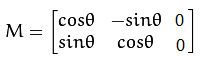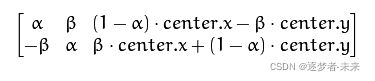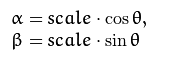opencv 学习笔记四 图形转换 图像缩放和仿射变换
1.图像缩放
CV_EXPORTS_W void resize( InputArray src, OutputArray dst,
Size dsize, double fx = 0, double fy = 0,
int interpolation = INTER_LINEAR );
@Param src 输入图像
@param dst 输出图像
@param dsize 输出矩阵的图像大小 为0时dsize = Size(round(fx*src.cols),round(fy*src.rows))
@param fx 水平轴的缩放因子
@param fy 垂直轴的缩放因子
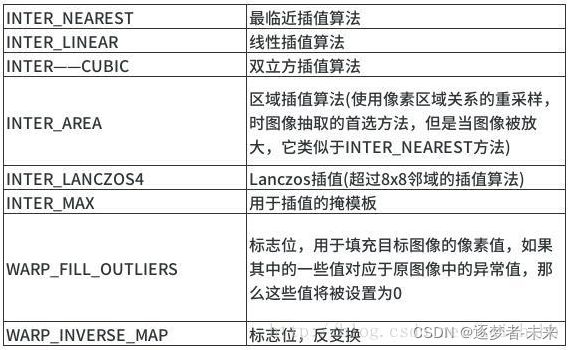
@param interpolation:插值算法
INTER_NEAREST : 最近邻插值法
INTER_LINEAR 默认值,双线性插值法
INTER_AREA 基于局部像素的重采样(resampling using pixel area relation)。对于图像抽取(image decimation)来说,这可能是一个更好的方法。但如果是放大图像时,它和最近邻法的效果类似。
INTER_CUBIC 基于4x4像素邻域的3次插值法
INTER_LANCZOS4 基于8x8像素邻域的Lanczos插值
常见用法:
INTER_AREA 适合于图像缩小;
INTER_CUBIC (slow) & INTER_LINEAR 适合于图像放大
程序源码:
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
RNG rng(12345);
Scalar color[7] = {
(Scalar(0,0,255)),//红色
(Scalar(0,255,0)),//绿色
(Scalar(255,0,0)),//蓝色
(Scalar(255,255,0)),//浅蓝色
(Scalar(255,0,255)),//紫色
(Scalar(0,255,255)),//黄色
(Scalar(128,128,192)),//浅粉色
};
int main()
{
Mat image,gray_img,thread_img,resize_img;
image = imread("../finger.jpg", 1);
if (image.empty()) {
cout << "无此图片" << endl;
return 0;
}
cvtColor(image, gray_img,COLOR_RGB2GRAY,0);//将图像转换为灰度图
threshold(gray_img, thread_img, 100, 255, THRESH_BINARY_INV);//将灰度图转换为二值图
while (1)
{
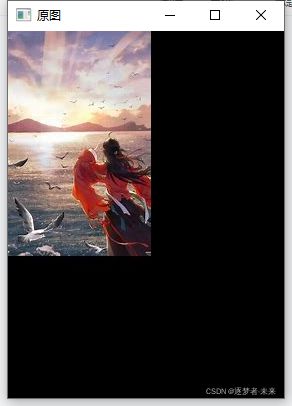
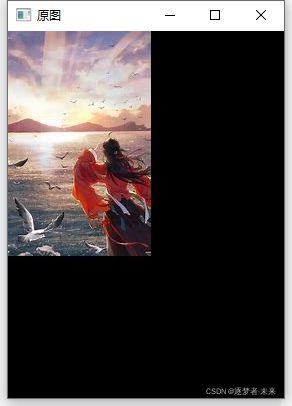
imshow("原图", image);
waitKey(1);
resize(image, resize_img, Size(0,0), 0.5f, 0.5f, INTER_AREA);
imshow("缩放图", resize_img);
waitKey(1);
2.仿射变换:
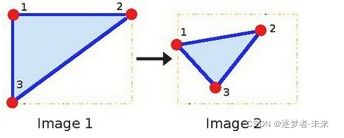
何为仿射变换?仿射变换的作用是什么?
从二维坐标到二维坐标直接的线性变换,且保持二维图形的平直性和平行性,仿射变换可以通过一系列的院子变换的复合来实现,其中包含平移、缩放、翻转、旋转和剪切;
仿射变换函数:
CV_EXPORTS_W void warpAffine( InputArray src, OutputArray dst,
InputArray M, Size dsize,
int flags = INTER_LINEAR,
int borderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar());
@param src 输入资源图像;
@param dst 输出目标图像;
@param M 2*3 转变矩阵;
@param dsize 输出矩阵的大小(cols,rows)即(width,height);
@param flags 插值算法标识符 默认值为INTER_LINEAR
@param borderMode 边界像素模式 默认值BORDER_CONSTANT
@param borderValue 边界取值,有默认值scalar()即0
常用插值法:
仿射变换的本质:即一个矩阵A和向量B共同组成的转变矩阵,和原图像坐标相乘来得到新的图像坐标,从而实现图像的移动和旋转等,如下矩阵A和向量B组成的转变矩阵M,来对原图像的坐标(X,Y)进行转变,得到新的坐标向量T
矩阵A和向量B:
仿射变换(矩阵计算):变换前的坐标为(x,y)
变换结果:变换后的坐标 (a00*x+a01*y+b00,a10*x+a11*x+b10)
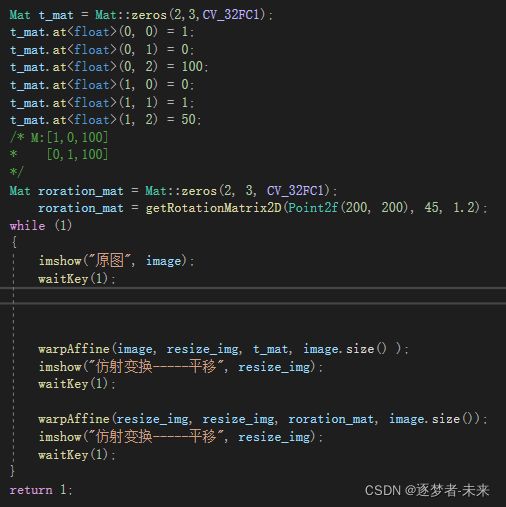
2.1 平移变换
认真理解完上面的公式;下面我们来实操一下平移变换
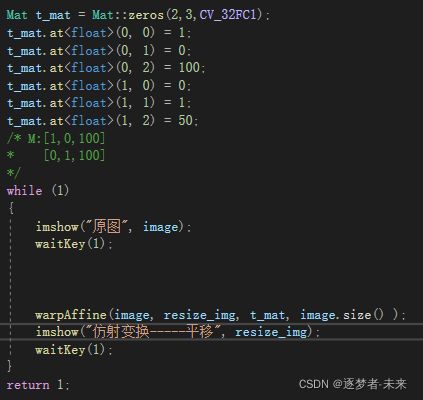
从(x,y)转变成(x+tx,y+ty)
程序源码:
2.2放大和缩小
放大和缩小指相对于原坐标(x,y),变换为了(a*x,b*y),即水平方向放大了a倍,垂直方向放大了b倍,起对应的转变矩阵如下:
2.3旋转变化
将(x,y),以坐标原点为中心,顺时针方向旋转a得到(x1,y1),有如下关系x1=xcosa-ysina,y1=xsina+ycosa;因此可以构建对应的转变矩阵如下:
opencv将其扩展到,任意点center为中心进行顺时针旋转a角度,放大scale倍的转变矩阵如下:
可通过getRotationMatrix2D()函数得到转变矩阵:
程序源码:
2.4仿射变换矩阵的计算
通过上述的平移,缩放,旋转的组合变化即可实现仿射变化,上述多个变换的变换矩阵相乘即能得到组合变换的矩阵。同时该变换矩阵设计到六个未知数(2*3矩阵),通过变换前后对应的三组表表,也可以求出变换矩阵,opencv提供了函数 getAffineTransform()来计算变化矩阵;
2.4.1矩阵相乘:将平移、旋转、缩放的变换矩阵相乘,最后即为仿射变换矩阵;
2.4.2 getAffineTransform():根据变换前后三组坐标来计算变换矩阵;
程序源码:
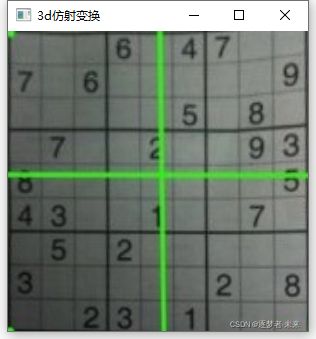
2.5透视变换
仿射变换都是在二维空间的变换,透视变换(投影变换)是在三维空间中发生了旋转。需要前后四组坐标来计算对应的转变矩阵,opencv提供了函数getPerspectiveTransform()来计算转变矩阵,warpPerspective()函数来进行透视变换,起对应的参数如下:
程序源码:
#include
#include
#include
#include
#include
using namespace cv;
using namespace std;
RNG rng(12345);
Scalar color[7] = {
(Scalar(0,0,255)),//红色
(Scalar(0,255,0)),//绿色
(Scalar(255,0,0)),//蓝色
(Scalar(255,255,0)),//浅蓝色
(Scalar(255,0,255)),//紫色
(Scalar(0,255,255)),//黄色
(Scalar(128,128,192)),//浅粉色
};
int main()
{
Mat image,gray_img,thread_img,resize_3d_img, resize2_img;
image = imread("../warpAffine_3d.jpg", 1);
if (image.empty()) {
cout << "无此图片" << endl;
return 0;
}
cvtColor(image, gray_img,COLOR_RGB2GRAY,0);//将图像转换为灰度图
threshold(gray_img, thread_img, 100, 255, THRESH_BINARY_INV);//将灰度图转换为二值图
Point2f srcM[4],dstM[4];
srcM[0] = Point2f(49, 47);//左上角绿色顶点
srcM[1] = Point2f(205, 47);//右上角绿色顶点
srcM[2] = Point2f(214, 204);//右下角绿色顶点
srcM[3] = Point2f(35, 205);//左下角绿色顶点
dstM[0] = Point2f(0, 0);
dstM[1] = Point2f(300, 0);
dstM[2] = Point2f(300, 300);
dstM[3] = Point2f(0, 300);
Mat t_mat = Mat::zeros(2, 4, CV_32FC1);
while (1)
{
imshow("原图", image);
waitKey(1);
t_mat = getPerspectiveTransform(srcM, dstM, 0);
warpPerspective(image, resize_3d_img, t_mat,Size(300,300),1,0,255);
imshow("3d仿射变换", resize_3d_img);
waitKey(1);
}
return 1;
}