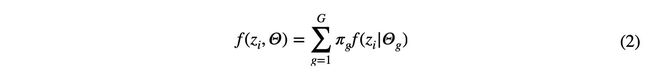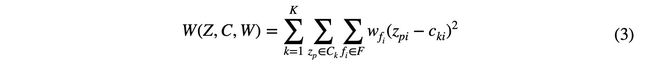A survey on feature selection approaches for clustering-聚类特征选择方法综述

Hancer, E., Xue, B. & Zhang, M. A survey on feature selection approaches for clustering.Artif Intell Rev 53, 4519–4545 (2020). https://doi.org/10.1007/s10462-019-09800-w

聚类特征选择方法综述

摘要

近年来数据的大规模增长给数据挖掘和机器学习任务带来了挑战。主要挑战之一是从原始可用特征集中选择相关特征，从而最大限度地提高原始特征集的学习性能。这一问题引起了研究者的关注，在文献中出现了各种成功的特征选择方法。尽管有一些关于无监督学习(例如聚类)的调查，但是在这些调查(例如用于聚类的基于进化计算的特征选择)中缺少大量关于无监督特征选择的工作来识别这些方法的优点和缺点。在本文中，我们通过从不同的角度反映当前方法的优点/缺点并确定未来研究的有希望的趋势，介绍了一个关于用于聚类的特征选择方法的全面综述。

关键词

聚类、特征选择、数据挖掘、进化计算

1 Introduction

随着计算机硬件、软件和在线数据库技术的发展，从不同来源收集和存储大规模数据集的可能性比以往任何时候都大。UCI机器学习知识库（Dheeru和Karra Taniskidou，2017年）也可以说明维度和实例数量的数据增长情况。然而，这种增长也给模式识别和知识发现过程带来了挑战，因为由于收集过程中使用的技术设备的缺陷或数据集本身的性质，数据中不仅可能存在所需的信息，而且可能存在各种噪声。例如，在扫描的数字地图中，当存在两个紧密间隔的对象时，扫描仪会腐蚀背景。这种噪声是数据性质的结果。同时，扫描仪的点扩展功能主要影响扫描地图的质量（Samet和Hancer 2012；Hancer等人2014）。另一个例子是，噪声、大气条件、恒定偏移和倾斜偏移只是在进一步处理高光谱图像处理之前需要处理的一些条件（Awad 2018；Amini et al.2018）。为了从这些数据集中提取有用的知识，通常需要数据预处理技术。

在数据预处理中，降维是一种众所周知的技术，它试图去除不相关的和冗余的特征，这些特征会降低进一步处理的性能(如分类、回归、随机森林和聚类)。降维技术可分为特征提取/构造和特征选择两类。在特征提取/构造中，通过从可用的原始特征中提取新的特征来降低数据的维数。特征提取的代表性方法有主成分分析(PCA) (Jolliffe 1986)、线性判别分析(LDA) (Ye 2007)和奇异值分解(SVD) (Golub and Reinsch 1970)等。另一方面，特征选择试图根据预定义的评价标准从所有可用特征中选择一个相关(原始)特征的小子集。一般来说，当数据集中有大量特征时，当用户想要构建一般化模型、降低计算复杂度、减少所需存储空间时，就需要特征选择。这些也可以通过特征提取来实现，但当模型或数据的可读性和可解释性很重要时，更需要特征选择，因为特征的原创性保持在缩小的空间中(Hancer et al. 2018)。

在监督学习的术语中，如果一个特征能够区分属于不同类别的实例，则该特征被称为相关或高度鉴别特征。换句话说，特征选择方法通常需要类标签来确定特征是否相关。然而，不仅在有监督的任务中，而且在无监督的任务中，高维度可能会对学习过程的性能产生不利影响，并且通常会导致大量的计算成本。当类别标签未知时（即在无监督学习方面），如何将特征定义为相关？在无监督学习中，不可能对相关性做出明确的定义。然而，在（Li等人，2016年）中提出，特征选择也可以从监督学习的不同角度提高无监督学习算法的性能，例如减少学习时间，简化学习的原型/模型，并帮助数据的可解释性和可视化。

聚类是无监督学习中最典型的任务之一，它是使用某种相似性准则将实例划分为组或簇的过程。每个簇在簇内具有最大的同质性，簇间具有最大的异质性。近年来，各种特征选择方法被设计并用于聚类，尽管它们与分类方法一样常见。文献中提供了一些调查，以确定这些方法中涉及的问题。Alelyani等人（2013年）考虑了聚类的特征加权方法。在本综述中，作者倾向于全面解释方法的总体时间表，而不是反映方法的缺点和优点。Amorim（2016）特别关注包装K-means算法的特征选择方法，并介绍了这些方法的比较研究。Mugunthadevi等人（2011年）回顾了为文档聚类提出的特征选择方法。然而，这次审查没有就这一问题进行全面的分析和讨论。在另一篇文章中，Liu和Yu（2005）回顾了分类和聚类的特征选择算法，并在三维框架中提出了特征选择方法的分类法。不幸的是，这种分类法不能被视为一般性的，因为只有少数研究被认为是建立分类法的，特别是对于聚类。Miruthula和Roopa（2015）提出了一项关于特征选择方法的研究，如链接无监督特征选择、空间光谱特征选择和稀疏回归。Li等人（2016年）回顾了从数据角度提出的用于聚类的特征选择方法，如流数据、链接数据和文本数据。另一项最近引入的研究（Solorio Fernandez et al.2019）回顾了聚类和分类任务中使用的各种无监督特征选择方法，然后对几种特征选择算法进行了全面的比较分析。与上述调查相比，它可以从不同角度提供新的见解，但缺少多种包装方法。总之，这些调查中缺少在这一领域开展的大多数现有和最近提出的研究，因此不可能从所有不同角度进行全面分析。特别是，据我们所知，为进化聚类设计的特征选择方法尚未在文献中得到充分考虑和讨论。为了缓解这一挑战，我们对聚类的特征选择方法进行了全面的调查，并简要讨论了存在的问题和未来趋势。这项调查的目标读者还包括对特征选择感兴趣的研究人员，以及博士等研究人员。希望了解该领域各种现有方法的学生。此外，本次调查还旨在吸引研究人员的兴趣，他们通常专注于开发用于分类的特征选择方法，关注设计用于解决聚类问题的特征选择方法。

本文的其余部分组织如下。

第2节介绍了特征选择和聚类的背景知识。

第3节回顾了为聚类设计的特征选择方法。

第4节阐述了具有未来趋势的方法的公开问题。

第5节总结了本文的一般结论。

2 Background

2.1 Feature selection

特征选择是去除对模型构建有不利影响的不相关和冗余特征的过程。预定义标准评估选定特征子集的最优性。由于特征选择保留了原始特征的原始含义，因此提供了更好的可读性和解释性，它已被广泛应用于各种数据挖掘和机器学习任务，如回归、分类和关联规则。过去，研究人员主要试图解释和分析监督学习任务中的特征选择，特别是由于特征选择在这些领域的流行而进行的分类（Dash和Liu，1999；Xue，2014）。特征选择基本上可以分为两种情况：有监督的特征选择和无监督的特征选择。当特征选择应用于无监督任务（如聚类）时，需要重新考虑特征选择的一般过程。通常，特征选择方法包括4个阶段，即选择、评估、停止标准和验证（Liu和Yu，2005）。在第一阶段，使用预定义的搜索策略（如完全搜索、顺序搜索和顺序浮动搜索）选择特征子集。在第二阶段，选择的特征子集将根据一定的标准进行评估。在满足停止准则后，从所有可能的子集中选择具有最佳评估值的子集。最后，使用验证度量对所选子集进行验证。在有监督和无监督的概念中，特征选择方法大致可分为以下几类：

• 过滤器试图根据数据的一般特征而不是学习算法来选择最佳特征子集。通常，过滤器根据特定的评估标准计算特征（子集）的分数。然后，他们选择得分最高的功能。评估标准可以是多变量的，也可以是单变量的。多变量度量考虑特征集内的多个双向关系，单变量测度独立地评估每个特征。因此，多变量度量可以检测冗余特征，因此被视为更一般的度量。

• 包装要求学习者评估可能的特征子集的优点。因此，包装器可以获得更好的特征子集，以增强预定义学习算法的性能，但它们往往比过滤器在计算上更密集。首先，包装器使用搜索策略获取特征子集。其次，通过学习算法评估所选特征子集的质量。重复此步骤，直到满足停止标准。

• 混合方法旨在获得包装器和过滤器的优点。两种杂交方法通常用于将包装物和过滤器杂交在一起。一种方法是应用两个阶段的过程，其中执行过滤方法以减少特征集，然后对减少的特征集执行包装方法以获得最终子集。另一种方法是使用过滤器（包装器）方法作为包装器（过滤器）方法中的本地搜索机制。后一种方法有望在学习性能和特征子集大小方面获得更好的性能。

• 嵌入式方法，被称为包装器和过滤器之间的折衷，将特征选择嵌入到学习算法的过程中。因此，它们利用了包装和过滤方法的特性。首先，它们与wrappers中的学习算法合作。其次，它们不需要多次使用学习算法，因此比包装器更有效。然而，嵌入式方法通常无法达到比包装器更好的学习性能。

一般来说，大多数过滤特征选择方法适用于分类数据集，因为过滤度量（如互信息）主要作用于离散变量。如果数据集包含连续变量或混合类型的变量，那么包装器方法可能会更好，因为有许多不同类型的学习算法可供选择来处理数据。嵌入式方法的使用在很大程度上取决于特定学习算法处理分类和/或连续数据的能力。当数据集具有大量特征和许多不相关特征时，通常使用混合方法。此外，具有少量记录的数据集通常更加困难，即不仅需要考虑哪种特征选择方法，而且还需要考虑如何应用特征选择方法来避免过度拟合或特征选择偏差的设计过程。然而，对于给定的数据集，最好的方法当然是具有微调参数并专门设计了特定预处理步骤的方法。

2.2 Clustering

聚类是使用预定义的相似性度量（如欧几里德距离、点对称性和汉明编码）对给定数据集中的未标记实例进行自动分组的过程。类似实例被确定为一个集群。特别是，每个簇通过其簇形心表示。聚类已广泛应用于各种数据挖掘和机器学习任务，包括图像分析、模式识别、信息检索和无线网络等。

文献中提出了大量的聚类方法。这些方法可大致分为分区、分层、基于密度和基于模型的方法（Hancer和Karaboga，2017）。

分区方法使用基于距离的度量将实例迭代地分配到集群。这些方法倾向于产生一个水平和不重叠的球形。属于这一类别的最具代表性的方法是K-均值（Macqueen 1967）、K-中值和模糊C-均值（FCM）（Bezdek等人，1984）。

分层方法试图通过将实例划分为不同的级别来构建层次结构。层次结构可以通过合并或拆分集群来构建。这一类的代表性方法有BIRCH（Zhang等人，1997年）、CURE（Guha等人，1998年）、DIANA（Patnaik等人，2016年）和ROCK（Guha等人，1998年）。

基于密度的方法试图通过考虑数据中区域的密度来检测聚类。低密度区域区分不同簇中的实例。这类最流行的方法是DBSCAN（Ester等人，1996年）、光学（Ankerst等人，1999年）和Dencule（He等人，b）。

基于模型的聚类尝试为数据假设一个统计模型，然后使用从该模型导出的概率作为聚类标准。基于模型的聚类的代表方法是期望最大化（McLachlan和Krishnan，2008）和高斯混合模型（McLachlan和Krishnan，2008）。有关集群的更多信息，请参见（Hancer和Karaboga 2017；Jain等人1999；Rui和Wunsch 2005）。

2.3 Fundamental clustering approaches

在本节中，我们将概述下一节将考虑的集群方法。

K-means：可以说是最流行的分区算法，K-means（Macqueen 1967）试图通过计算每个实例到另一个实例的欧几里德距离来迭代地将数据实例分配到集群中。

对于给定的数据集Z，K-均值的输出是一组不相交的聚类C=C1,C2,...,Ck,...,CK，其中每个簇CK由簇质心mk表示mk ∈ M、 M={m1，m2，…，mK}。质心mk在Ck内的欧几里德距离之和最小。换句话说，K-means迭代地尝试最小化数据实例之间的集群内距离（zp ∈ Ck）和各自的质心mk ∈ M ，定义如下。

其中mki表示第k个质心（mk）的第i个特征，F是表示N个特征的特征集，例如F={f1，f2，…，fi，…，fN}。

K-means的一般顺序如下：

1. 通过从数据集中选择实例或在预定义边界内随机生成，初始化一组集群C，

2. 通过欧几里德距离将每个实例zp分配给其最近的簇mk，

3. 更新每个簇的质心mk∈ M取Ck内所有实例的平均值，

4. 转至步骤2并重复该过程，直到满足特定要求。

基于模型的聚类：混合模型扩展了数据分析师可用的聚类分析。混合模型在概率方案中定义集群的结构。如果使用多元高斯分布的有限混合设计聚类，则将概率分布预先指定为观测数据的数据生成过程。特别是，假设每个簇中的数据和组合数据源分别由多元高斯分布和多元高斯分布的凸组合生成（Grün 2019）。混合模型中使用的一般分布如下所示：

其中zi=（zi1，zi2，…，ziM）是表示Z的第i个实例的M维向量，g表示gth群的混合概率，以及g表示gth组的参数集。

与K-均值相比，高斯混合模型允许具有不同大小和不同体积的簇。此外，集群独立于用于变量的缩放（除了潜在的数值问题）。总之，混合模型的一般工作概念是灵活的，但有点复杂。进化聚类：作为人工智能的一门创新学科，进化计算（EC）技术被认为是解决NP难问题的有效元启发式方法。特别是，EC技术（Zhao et al.2017；Parvin et al.2012）可以在合理的时间内为此类问题提供最优或接近最优的解决方案。电子商务技术主要包括两大类：进化算法和群体智能算法。前者遵循突变、重组和选择等基本生物学术语。这一类的代表性方法是遗传算法（GAs）（Holland 1975）、遗传规划（GP）（Koza 1992）和差分进化（DE）（Storn和Price 1997）。后者的灵感来自昆虫或动物的智能行为，如鸟类、蚂蚁、蜜蜂和细菌群。这类最流行的例子是粒子群优化（PSO）（Kennedy和Eberhart 1995）、蚁群优化（ACO）（Dorigo和Di Caro 1999）和人工蜂群（ABC）（Karaboga等人，2014）。

由于聚类被认为是一个NP难问题（Aloise et al.2009），EC技术已被广泛用于开发聚类方法，尤其是分区方法。有关聚类EC技术的更多信息，请参见（Hancer和Karaboga 2017；Hruschka等人，2009）。基于EC的聚类方法的一般机制可描述如下：

1. 使用K个簇质心初始化总体中的每个解。

2. 对每个当前解决方案执行预定义的进化运算符以生成新的解决方案。

3. 使用预定义的距离度量（例如，欧几里德距离），将数据实例指定给新解决方案中的每个簇质心。

4. 通过预定义的聚类标准评估新解决方案的适应度值[例如，公式（1）]。

5. 如果新解的适应度值优于其当前解，则新解将保留在总体中，而不是其当前解。

6. 重复步骤2-5，直到满足最大迭代次数或预定义的停止标准。

7. 选择在总体中具有最佳适应度值的解决方案作为最终簇质心。

2.4 Principles of feature selection for clustering

从聚类的角度来看，数据中的无关和冗余特征可能会降低聚类的质量，导致较高的计算成本，并需要更多的内存。因此，消除这些不相关和冗余的特性可以缓解这些问题。为了说明这一概念，我们提供了图1（Li等人，2016）。根据图1，f1足以区分簇。另一方面，被称为不相关的f2对聚类过程没有额外影响，而被称为冗余的f3对聚类的同质性产生不利影响。此外，包含相关特征的不同特征子集可产生不同的聚类。例如，当添加到特征子集时，相关特征可能有助于发现隐藏的数据模式。因此，各种特征选择方法被提出用于聚类方法中，以通过消除无关和冗余特征来提高聚类性能。

与分类中的特征选择类似，提出的用于聚类的特征选择方法可以分为过滤方法、包装方法、嵌入方法和混合方法。然而，关于聚类中嵌入和混合特征选择方法的研究却少得多。包装器依赖于聚类算法来评估选定特征子集的聚类质量，而过滤器独立于聚类算法。与wrappers一样，嵌入式方法也可以使用聚类算法，但与wrappers不同的是，它结合了与特定聚类结构相关的知识。另一种方法是混合方法，它将过滤器和包装器方法结合到一个策略中。

图1显示不相关和冗余特征如何影响聚类的示例（Li等人，2016）

子空间聚类作为特征选择的一种扩展，试图在同一数据集的不同子空间中找到聚类结构。与特征选择一样，子空间聚类也需要搜索策略和评估度量。此外，子空间聚类必须考虑限制评估度量的范围，以考虑每个不同簇的不同子空间。在本文中，我们没有深入考虑子空间聚类方法来防止在研究中添加大量的页面，但是我们将讨论一些最新的子空间聚类算法，这些算法主要是在包装方法的范畴中。有关子空间聚类的更多信息，请参见Parsons et al.（2004），Domeniconi et al.（2004）。

3 Feature selection approaches for clustering

我们研究了四类用于聚类的特征选择方法，即过滤、包装、嵌入和混合方法。由于有更多的方法属于包装器方法，我们将包装器方法进一步划分为子类别，即：具有K-均值的特征选择方法、基于模型聚类的特征选择方法和具有进化聚类的特征选择方法。图2显示了本文中回顾的方法的分类。

图2用于聚类的特征选择方法的分类

3.1 Filterapproaches

过滤器根据要素的特征选择数据中的要素。与包装器相比，过滤器不需要任何聚类/学习算法，因此比包装器更有效。过滤器不是通过聚类算法评估数据的聚类性能，而是直接评估数据中特征的统计性能，更适合于大规模数据集。因此，过滤器的聚类性能通常低于包装器。关注过滤器的作品数量远少于文献中关于包装的作品数量。

各种标准被用来定义数据中特征的相关性。在这些标准中，有些标准使用数据相似性来衡量特征重要性，称为基于相似性的方法（Li等人，2016）。在有监督特征选择方面，可以通过标签信息获得数据相似性。另一方面，在无监督特征选择方面，通过实例间的两两相似性对数据中的所有特征进行单独评估，然后选择一个保持效用最大化的特征子集。

Mitra等人（2002年）提出了一种过滤方法，该方法基于一种称为最大信息压缩指数（MICI）的基于方差的度量来测量特征之间的相关性。该方法的总体目标是使用knn的原理将特征划分为多个簇，即同一簇内的特征彼此相似，而不同簇内的特征则不同。在每次迭代中，根据MICI准则为每个特征找到k个最近的特征。然后，选择特征，该特征使用k个最近的特征构建最紧凑的子集。重复此过程，直到选择或放弃所有特征。Mitra工作的改进版本（Li et al.2007）应用（Mitra et al.2002）中的特征选择方法去除冗余特征，然后使用指数熵标准根据其相关性对剩余特征进行排序。最后，使用前向搜索机制和模糊评价指数（FFEI）选择特征子集。

He等人（2005年）介绍了一种过滤器方法（称为拉普拉斯分数），其目的是根据局部保持能力选择特征。拉普拉斯分数可以应用于无监督问题和有监督问题。为了测试拉普拉斯评分的性能，首先将其应用于人脸图像聚类。根据结果，它的表现优于方差得分，方差得分通常会消除所有零方差特征。但是，特征子集大小应由用户预先指定。光谱特征选择（SPEC）算法（Zhao和Liu，2007）作为拉普拉斯分数的一种特殊情况，使用径向基函数作为相似函数来评估特征相关性。相关特征应具有相近的相似性值。实验结果表明，它的性能优于拉普拉斯评分。

Haindl等人（2006年）介绍了一种基于皮尔逊相关系数的滤波方法。该方法首先计算数据中特征之间所有可能的成对相关性，然后删除与其他特征具有最高平均相关性的特征。对于用户指定的许多功能，重复此过程。为无监督和监督任务设计的另一种过滤器特征选择方法（称为相关冗余特征选择（RRFS））（Ferreira和Figueiredo 2012）涉及两个阶段。对于无监督方案，在第一阶段，根据方差准则对特征进行排序。在第二阶段中，使用方差准则根据冗余度对排序特征进行评估。然后，选择冗余度最低的m个特征作为特征子集。

Nie等人（2008年）介绍了一种过滤方法，该方法使用散射跟踪标准选择特征。该方法构造两个相似矩阵来度量簇内距离和簇间分离。然而，散射迹线准则不包括封闭形式的解，因此难以考虑。为了解决这个问题，分散跟踪标准通常被重新制定为更合适的格式，称为比率跟踪，例如，Wang等人（2007）开发了一种迭代优化分散跟踪标准的策略。

Li等人（2008）基于散射跟踪准则提出了一种局部特征选择方法。Li等人2008年的研究表明，由于以下原因，簇内距离和簇间分离需要标准化。首先，散射轨迹随着维数的增加而单调增加，而聚类分配没有变化。第二点也是最后一点，这种方法尝试为每个集群选择不同的特征子集。为了对簇内距离和簇间分离执行归一化，在单个簇集上执行交叉投影。在该方法中，首先在所有可用特征上生成一个聚类集，然后执行顺序向后选择以消除不相关和冗余的特征。因此，可以认为，对于具有大量特征的数据集，计算成本可能非常高。

Vandenbroucke等人（2000年）介绍了一种用于足球图像分割的滤波方法。首先，通过RGB和CIE等不同颜色空间考虑像素值，从源图像中获得许多纹理颜色特征。然后，使用一种散射跟踪准则将原始特征集分类为若干特征子集。对于每个可能的特征子集，计算散射准则的值，并选择使散射准则最大化的特征子集来确定候选特征。如果候选特征与选定特征高度相关，则放弃该特征。虽然这种方法产生了很好的分割性能，但它是专门为分割足球图像而设计的，并且没有在不同类型的图像数据集上进行测试。

3.2 Wrapper approaches

与过滤器方法不同，包装器方法是为特定的聚类算法设计的。换句话说，包装器与聚类算法同步工作，因此与过滤器相比，包装器通常能够达到更好的聚类性能。在本节中，我们将介绍并讨论专门为K-means、基于模型和基于进化计算的聚类算法设计的包装器方法。

3.2.1 Feature selection for K‐means

尽管K-means很受欢迎，但与数据挖掘中的任何其他算法一样，它也有不足之处。首先，K-means的聚类性能非常依赖于初始聚类集。其次，集群K的数量需要由用户预定义。第三，它可能会收敛到局部极小值，因为它执行贪婪搜索。第四也是最后一点，它假设所有特征都同等重要，而不是考虑它们的实际关联程度。由于我们研究的总体目标，我们特别关注处理最后一个缺陷的方法。

K-means以同等重要性评估每个特征。换句话说，即使定义为不太相关、不相关或冗余的每个特征对聚类过程也有相同的贡献。然而，（Chakraborty和Das 2018）指出，如果集群过程中存在大量不相关和冗余的特征，集群的质量可能会非常低。此外，K-means很可能因不相关和冗余特征的存在而受到负面影响。通过为每个特征分配权重（称为特征权重）解决了此缺点。特征选择假设所选子集中的所有相关特征具有相同的程度，即，仅存在两种情况，即特征子集可选择或不选择特征。特征权重假设所选子集中的每个特征不能具有相同的关联度。相反，它为每个特征指定一个权重，该权重通常在0和1之间。因此，特征加权可以被视为特征选择的一般版本。从公式（1）定义的K-均值的理论角度来看，为K-均值提出的特征加权方法的广义标准可定义如下：

其中Wfi是子集F中的特征fi的权重，而zpi表示数据中的第p个实例的第i个功能。

在这一领域，自20世纪80年代以来，针对K-means开发了多种特征加权方法。在这项研究中，我们试图讨论最流行和最具创新性的。综合聚类（SYNCLUS）（DeSarbo和Cron 1988）被视为K-means中使用的第一种加权方法。除了表示每个特征相关性程度的权重外，SYNCLUS还考虑了特征组的权重。与K-means一样，第一步要求用户提供集群数量和输入数据。虽然这是该领域的初步工作，但它的计算成本可能很高，并且其性能在很大程度上取决于参数值。然而，研究人员试图使用不同的技术来扩展其性能，如Polak-Rebiere优化方案（Polak 1969）和特征的一般线性变换。与SYNCLUS类似，FGK means考虑两种类型的权重，分别用于特征和特征组。然而，与SYNCLUS不同，要素组的权重不需要由用户预定义。在FG-K-means中，目标函数是通过将这两种类型的权重作为两个不同的分量引入由等式（1）定义的K-means标准中来设计的。两个控制参数保持了分量和K-均值准则之间的平衡。但是，确定哪些控制参数值更适合数据集并不容易。

凸K-means（CK-means）方法（Modha和Spangler 2003）通过根据数据集考虑不同的特征空间，在K-means中集成了自适应加权方案。CK是指以最小化聚类距离内的平均值为目标，尝试迭代确定特征集的最佳权重。取得了可喜的成果；然而，由于梯度下降搜索，它不能保证最优权重，并且可能收敛到局部极小值。Tsai和Chio（2008）将另一种不同的K-均值加权方案（FWSA）设计为优化问题。在该方案中，通过同时最小化簇内距离和最大化簇间分离来更新特征权重。与K-均值的其他加权方法不同，FWSA不需要预定义的参数。

为K-均值提出的另一种特征加权方法，属性加权聚类（AWK）（Chan et al.2004）假设每个特征在不同的聚类中可能具有不同的相关性权重。AWK的目标是最小化集群内的加权距离之和。Huang等人（2005）提出了与AWK非常相似的加权K均值（WK均值）。然而，WKmeans中每个特征只有一个权重。WK均值也被集成到模糊聚类中。与后一种不同的是，这种变体允许对不同的聚类使用不同的相关性权重。WK均值及其变体也取得了令人满意的结果，但高度依赖于预定义的控制参数，该参数将权重保持在合理水平。此外，还没有这样明确的策略来预先定义此控制参数。Ji等人（2013）介绍了一种改进的k-原型聚类方法（IK-P），其目的是最小化WKmeans标准。IK-P能够通过应用两个距离标准来处理数字和分类特征，分别是：（1）曼哈顿距离和（2）基于频率的距离。与k-prototype和KL-FCM-GM相比，IK-P产生了有希望的结果（Chatzis 2011）。De Amorim和Mirkin（2016）提出了WK手段的另一个延伸，即智能WK手段（iMWKmeans）。与以前的Wk-means不同，iMWK-means可以借助Minkowski评分自动检测数据中的聚类数或聚类结构，同时确定特征权重。

熵权K-均值（EW-KM）方法（Jing等人，2007）最大化负熵，并最小化簇内距离，以处理仅使用几个维度识别此类簇的相关问题。根据Jing等人（2007）报告的结果，EW-KM优于许多聚类方法。然而，很难预先确定簇内距离和负熵之间的控制参数。

受K-means和局部自适应聚类算法（Domeniconi et al.2007）的启发，Parvin et al.（2013、2015）引入了加权局部聚类算法（WLAC和FWLAC）。与K-means一样，WLAC和FWLAC首先选择K个分散良好的点作为初始质心，然后尝试通过探索质心附近的子空间来改进初始质心、特征权重和聚类权重。然而，它们的性能对控制参数非常敏感。

3.2.2 Feature selection for model‐based clustering

基于模型的聚类通常考虑建模中的所有特征。然而，在许多情况下，这增加了构建模型的复杂性。如前几小节所述，某些功能可能对聚类过程不利，甚至可能有害。尽管假设所有特征都包含聚类信息，但由于一般术语（称为维数灾难）的缘故，这可能会有问题。特别是近年来，许多基于模型的特征选择方法被开发用于聚类。由于页面的限制，我们将只关注最典型的页面。有关这一问题的更多信息，请参阅（Fop等人，2018年）中最近的讨论。

Vaithyanathan和Dom（1999）介绍了一种贝叶斯方法，该方法通过边缘和综合可能性找到最佳模型。该方法通过将特征划分为簇，然后消除具有不相关和冗余特征的特征簇来选择特征。特征分组性能对特征选择过程有很大影响。Dy和Brodley（2004）引入了一个包装器框架（FSSM）来执行聚类中的特征选择。在FSSM中，特征选择采用顺序前向搜索，聚类算法采用期望最大化；最大似然准则和散射跟踪准则分别用于特征选择过程。为了恢复最大似然准则和散射跟踪准则的偏差问题，采用了归一化过程。根据大量实验，特征选择被证明在聚类任务中起着至关重要的作用，特别是在噪声问题上。尽管执行了标准化，但FSSM中特征选择过程的偏差问题无法完全避免。Tadesse等人（2005年）介绍了一种贝叶斯方法，该方法使用潜在变量（特征）来识别鉴别特征。在该方法中，使用可逆跳跃马尔可夫链方法来创建或删除簇。Kim等人（2006年）介绍了一种类似的方法，通过Dirichlet混合根据无限混合分布重新设计聚类。这些方法不考虑聚类的相关和不相关特征之间的相关性。

Raftery和Dean（2006）介绍了一种用于基于模型的聚类的特征选择方法。特征被视为两个嵌套集，其中一个包含携带聚类信息的相关和不相关特征，而另一个包含冗余特征的集合在条件上独立于另一个集合。特征选择是通过比较这两个嵌套集在贪婪搜索机制上的贝叶斯因子来实现的。然而，这并不保证获得最佳特征子集。此外，由于通过贝叶斯规则比较嵌套集，这种方法可能非常耗时。在（Tadesse et al.2005；Kim et al.2006；Raftery and Dean 2006）中，假设无关特征通过线性回归依赖于相关特征，即无关和相关特征不是完全独立的。回归中的这一假设需要额外的参数，但不能显著提高聚类性能。Maugis et al.（2005）提出了Raftery和Dean（2006）的扩展版本，通过在回归中贪婪地选择特征，允许一些不相关的特征独立于相关特征。通过这种方式，其目的是提高集群性能。然而，该方法的总体时间表变得更加复杂。

Zeng和Cheung（2006）开发了一种具有特征权重的竞争对手惩罚期望最大化算法（RPEM）（FW-RPEM），以同时执行聚类和特征选择。在该方法中，使用马尔可夫覆盖滤波器消除冗余特征。它的性能优于RPEM，但实验仅在三个数据集上进行。

3.2.3 Feature selection for evolutionary clustering

由于其有效的全局搜索能力，进化聚类技术已被应用于解决集群以及其他各种领域。根据大量文献研究（Hancer et al.2012、2013；Ozturk et al.2015），基于EC的聚类方法可以比众所周知的聚类方法（如K-means和FCM）实现更好的聚类性能。然而，数据中的无关和冗余特征也可能会降低基于EC的聚类方法的性能。与聚类相关的另一个重要问题是，目前数据的聚类结构（例如，聚类数量）大多未知。此外，手动确定数据中的群集结构或群集数量并不容易。为了涵盖这些问题，EC技术在聚类和特征选择方面的通用标准可定义如下（Sheng等人，2005年）。

其中VI表示内部有效性指数，用于测量生成的聚类的优度；Dweight表示分数或高斯函数，用于测量选定子集大小与所有特征数量的比率；Kweight表示高斯函数，用于测量确定的聚类数的分布。有关更多信息，请参阅（Hancer 2018）。

本文研究的进化聚类特征选择方法将从目标数的角度进一步讨论，即单目标方法和多目标方法。

（1） 单目标方法Sheng et al.（2005）提出了一种变长遗传算法，称为NMA-CFS，它在进行聚类的同时选择特征。在该方法中，使用散射跟踪准则来评估簇的优度。作为基于EC的同时聚类和特征选择的首次研究，NMA-CFS取得了令人满意的结果，但实验中使用的数据集仅包含少量特征和相对较少的聚类。换句话说，当特性和集群数量增加时，NMA-CFS的性能如何尚不清楚。此外，在计算散射轨迹时，不仅使用选定的特征，还使用所有特征，因为该标准往往偏向于大量特征。Das等人（2016年）介绍了一种基于遗传算法的同时聚类和特征选择方法。为了评估解的优度，以加权方式使用DBI指数（Davies和Bouldin 1979）和特征数。为了防止DBI索引计算过程中出现偏差，使用了所有特征，而不仅仅是选定的特征。尽管实验结果显示了基于遗传算法的方法相对于FCM的优越性，但性能仅通过最佳解进行评估，而没有考虑算法的随机性，该算法要求根据多个解的平均值进行评估。

Sarvari等人（2010年）使用和声搜索（HS）算法和基于质心的编码方案重新设计了NMA-CFS的概念。Cobos等人（2010年）介绍了一种混合K-means和HS（IHSK）方法，用于同时执行聚类和特征选择。在IHSK中，一个局部的add-remove操作符被顺序地执行以选择特征子集，因此适应度函数不包括Dweight分量。如果通过在特征子集中添加（删除）任何特征可以达到比当前适应值更好的适应值，则将选择（删除）该特征。因此，在计算聚类有效性准则时，仅使用选定的特征。IHSK中的另一个局部搜索模块K-means进行了几次迭代，以减少初始条件的不利影响。从结果可以推断，IHSK可以比NMA-CFS和K-means等多种方法获得更好的性能。然而，它只在三个真实数据集上进行了测试。

Swetha和Devi（2012）介绍了一种基于两阶段粒子群优化（PSO）的聚类方法，该方法首先执行特征选择，然后对选定的特征子集应用聚类。Javani等人（2011）介绍了另一种基于PSO的同时聚类和特征选择方法。在该方法中，定义了一个新的核化有效性指数，并概率地调用K-均值，以减少初始条件在进化过程中的不利影响。然而，这种方法并没有在高维数据集上进行测试。Prakash等人（2015年）介绍了一种用于同时聚类和特征选择的混合K-均值和二进制PSO方法（BPSO-X）。在BPSO-X中，每个解决方案通过表示可能的特征子集的0和1进行编码。为了评估解决方案的质量，BPSO-X首先选择可能的特征子集，然后对缩减后的数据集执行K-means以获得聚类。在K-均值之后，使用轮廓指数（Rousseeuw 1987）对获得的聚类进行评估。与IHSK一样，BPSO-X也会考虑选定的特征子集来构造聚类。尽管在（Prakash和Singh，2015年）通过比较BPSO-X与BPSO和GA在各种数据集上进行了大量实验，但由于以下缺点，不可能进行一致性分析。首先，在比较中没有使用传统的聚类方法，如K-均值和FCM。其次，在外部有效性指标方面，仅报告了最佳解决方案的结果。

Lensen等人（2016年）开发了基于PSO的方法，使用基于分区和基于质心的表示方案同时进行聚类和特征选择。受NMA-CFS的启发，基于粒子群算法的方法使用了一种散射跟踪准则和相同的特征加权方案（Kweight）。另一方面，与NMA-CFS不同，基于PSO的方法使用指定的对数函数作为KWweight的分量来自动识别集群结构。结果表明，当K为固定值时，基于划分的表示方案比基于质心的编码方案表现更好。然而，对于具有大量实例的数据集，基于分区的编码方案可能需要大量计算。Lensen等人（2017年）还开发了一种基于多阶段PSO的方法。在第一阶段，使用轮廓法（Rousseeuw 1987）获得初始簇数（Kest）。在第二阶段，使用基于分区的PSO方法同时执行聚类和特征选择过程。特别是，前一阶段获得的Kest值在此阶段用作平均参数，以建立高斯加权函数来确定适当的簇数。此外，还设计了一种高斯函数，用于从所有可用特征中选择特征子集。在最后一个阶段，将基于分区的编码方案转换为基于质心的编码方案，然后使用另一个PSO搜索过程对质心进行微调。从结果可以看出，它通常比以前基于粒子群优化的方法表现得更好。然而，它无法在实际数据集中正确地检测最佳聚类数。

Hancer（2018）引入了一种基于DE的方法，以同时执行聚类和特征选择。在该方法中，使用基于相似性方案的离散去变量来进化解，并通过对Turi的VI指数（Turi 2001）采用一种高斯特征加权函数来改进新的目标函数。根据结果，尽管缺乏关于聚类数量的信息，但它通常比传统的聚类方法（如K-means和FCM）表现得更好。此外，在检测最佳特征数量方面，它也比之前描述的基于PSO的方法（Lensen等人，2016年、2017年）取得了更好的性能。然而，这些基于DE的和基于PSO的方法在计算聚类有效性标准期间都使用所有特征，以防止特征选择导致对少量聚类的偏见。

（2） 多目标方法同时聚类和特征选择任务也被视为一个多目标问题。Kim等人（2002年）介绍了一种使用进化局部选择算法和K-均值的多目标算法（ELSA）。为了评估聚类的质量，在ELSA算法中分别使用一种类型的簇内距离和簇间分离作为目标。然而，这些目标需要依赖于数据的常数，这些常数需要根据数据集进行指定。

Dutta（2012、2013）提出了基于多目标遗传算法的同时聚类和特征选择方法。与以前的方法不同，这些方法假设K是固定的。采用一类簇内距离和簇间分离作为目标来评价解的优度。结果表明，该算法的性能优于K-means算法和多目标聚类算法。但是，由于性能分析仅通过内部指标进行，因此不可能进行一致性分析。

Saha等人（2014、2015）介绍了基于多目标模拟退火的同时聚类和特征选择方法。与以前的多目标方法相比，它考虑了两个以上的目标，即Sym指数、XB指数、特征数量和调整后的兰德指数（对于监督版本）。在有效性标准的计算过程中，仅使用在个体中表示的选定特征。为了在最终帕累托前沿选择最佳解决方案，假定数据集中少量实例的类标签由用户已知，称为测试实例。由于最终帕累托前沿上的每个解决方案都提供了一组聚类，因此为每个测试样本分配了一个聚类标签。然后，使用聚类标签和类标签计算最终帕累托前沿上每个解的Minkowski分数。选择得分最高的解决方案作为最终解决方案。尽管他们针对各种聚类方法（如VGAPS和K-means）取得了有希望的结果，但他们只在具有2个或3个聚类的数据集上检查了算法。

在另一项研究中，Saha等人（2018年）引入了一种基于多目标DE的方法（自动模式）来识别微RNA。与以前的多目标方法相比，自动模式使用了一种加权方案，与K-均值方法类似，用于选择最佳特征子集。在自动模式下，使用加权版本的谢贝尼指数（谢贝尼和贝尼1991）和I指数（Bandyopadhyay和Saha 2012）作为目标。因此，所选特征子集大小不需要被视为目标。通过大量的实验比较了各种聚类方法，自动模式在小RNA问题中取得了良好的聚类质量。然而，聚类质量仅通过内部指标进行分析。

Prakash和Singh（2019）介绍了一种遗传启发的基于二元引力搜索的同时聚类和特征选择方法（IMBGSAFS）。在IMBGSAFS中，轮廓索引（Rousseeuw 1987）和特征子集大小是用于搜索可能的解决方案空间的目标，外部存档用于构建非支配解决方案集。对于聚类，使用解决方案中选定的特征对缩减的数据集应用K-means。经过进化过程，选择具有最佳F-测度得分的解作为最终解。根据结果，IMBGSAFS的表现优于精英非支配排序GA（NSGAII（Deb等人，2002））。为了使用NSGAII获得更好的结果，可以重新设计改进的NSGAII变体（Lee et al.2017；Song and Chen 2018；Gao et al.2019），并将其用于同时聚类和特征选择。

Hancer（2020）介绍了一种基于可变字符串长度的多目标DE方法（MODE-CFS），用于同时聚类和特征选择。为了评估解决方案的优点，MODE-CFS同时最大化轮廓指数（Rousseeuw 1987）和选定特征的数量，同时最小化WB指数。最大化特征数量的总体目标是防止在评估有效性指标的实例之间的距离计算过程中出现重叠问题。对于每个解，使用指定的两种情况突变方案生成突变解，然后将当前解及其突变添加到并集。最后，应用非支配排序方案为下一代找到更合适的解决方案。在进化过程结束时，使用Saha等人（2014、2015）提出的半监督选择方案选择单个解决方案。根据结果，它优于各种传统的和最近引入的多目标聚类方法。

3.3 Embedded approaches

嵌入式方法将特征子集选择过程作为学习过程的一部分。因此，嵌入式方法在计算上比包装器方法便宜。对于嵌入式方法，稀疏学习算法由于其性能和可解释性而具有非常重要的作用。稀疏学习算法的目标是在一些优度度量和结果的稀疏性之间寻求一种折衷。例如，在稀疏学习集群任务中，集群质量或其他一些典型的性能度量不是唯一的关注点：我们还希望能够澄清集群方法对非专家用户意味着什么。因此，如果在聚类过程中考虑生物医学数据，我们应该提供一种聚类方法，该方法可以实现高质量的聚类，但也可以用一些特征来表示生物医学数据。

近年来，将稀疏学习应用于聚类的思想引起了研究者的关注。通常，这些方法首先使用聚类算法找到聚类标签，然后通过生成的聚类标签将无监督的特征选择转换为有监督的上下文。特别是，它的目的是保留从整个特征空间约束的流形结构。嵌入式稀疏学习方法的流程图如图3所示。

作为最早提出的用于聚类的稀疏学习特征选择方法，多聚类特征选择（MCFS）（2010）分为三个阶段。在第一阶段，光谱分析用于探索内在结构，即测量特征之间的相关性。在第二阶段，使用L1正则化最小二乘回归模型来量化特征的重要性。在最后一个阶段，选择具有通过前一阶段获得的最高系数值的指定数量的特征。尽管MCFS已被证明是一种设计良好的方法来解决集群的特征选择问题，但它的计算成本很高。为了提高MCF的效率，Wang和Shen（2016）在MCF中整合了位置敏感的hasing森林（Bawa et al.2005）。MCFS的另一个变体（MCFS-SDS）（Liu和Liu 2012）通过平滑分布分数同时评估L1正则化最小二乘和L2正则化最小二乘进行了改进。因此，MCFS-SDS比纯MCFS更有效，尤其是对于少量簇。

MRSF（Zhao et al.2010）将特征选择任务视为一个多输出回归问题，并应用L2,1-正则化最小二乘法代替L1-正则化最小二乘法，这是另一种早期针对聚类提出的稀疏学习特征选择方法。受MRSF的启发，Yang等人（2011）介绍了一种无监督特征选择方法（UDFS），该方法利用了特征相关性和散射矩阵中包含的局部鉴别信息。通过使用局部信息，UDF很好地保留了集群结构。对于特征子集的选择，使用了带有一些附加约束的L2,1-范数正则化子。非负鉴别特征选择（NDFS）（Li et al.2012）包括与UDF相似的特性，同时执行光谱聚类和特征选择。通过谱聚类得到聚类标签进行特征选择。非负约束适用于类标签，以获得更精确的簇标签。对于特征选择过程，使用L2正则化最小二乘法。

为了处理数据中的噪声，钱和翟（2013）介绍了一种用于聚类的谱学习特征选择算法，称为鲁棒无监督特征选择（RUFS）。与MCF、UDF和NDF不同，聚类标签是使用局部学习正则化非负矩阵分解确定的。对于特征选择，在确定簇标签时使用稳健的联合L2,1-范数。遵循与RUFS类似的概念，通过矩阵分解的鲁棒无监督特征选择（RUFSM）（Du et al.2017）同时通过L2,1-范数执行鉴别特征选择和鲁棒聚类以选择特征。与RUF不同，RUFSM使用簇质心而不是簇标签。

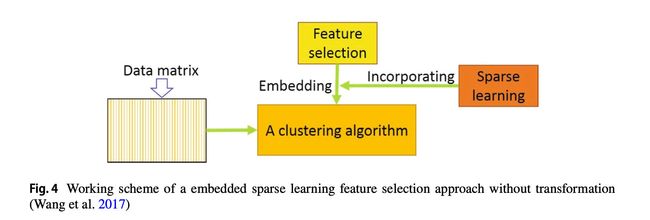
如图3所示，传统的嵌入式稀疏学习特征选择方法（如MCFS、NDFS和RUFS）要求由聚类算法生成的聚类标签将无监督特征选择转换为有监督特征选择。然而，这种转换通常会导致非最优特征子集。为了解决这个问题，Wang等人（2017）提出了一种新的嵌入式方法，称为嵌入式无监督特征选择（EUFS），该方法直接将特征选择嵌入到聚类算法中，而无需转换。EUFS通过最小化重构误差来应用K均值来获得聚类标签并选择特征。然而，EUFS倾向于选择可能是非歧视性的大幅度特征。为了解决这一问题，Zhu和Yang（2018）提出了判别式嵌入式无监督特征选择方法（DEUFS），该方法通过最大化聚类之间的异质性来获得聚类标签，从而对数据的聚类结构进行建模。EUFS和DEUFS方法的一般流程图如图4所示。

如第2.1节所述，过滤器通常比包装器在更短的时间内完成特征子集的选择过程。另一方面，过滤器不能像包装器一样提高学习算法的性能。这是因为包装器与学习算法同步工作。为了发挥包装器和过滤器的优势，即提高选择过程的计算效率和进一步学习过程的性能，混合包装器过滤器方法在文献中非常常见（Hancer 2019）。

Dash和Liu（2000）介绍了一种用于聚类的混合双向特征选择方法。在第一阶段，基于信息论的熵测度对特征进行排序。为了对特征进行排序，将从可用特征集中删除每个特征，并通过计算剩余特征集的熵来测量其退化效果。在第二阶段，从排名靠前的特征集中选择排名靠前的特征，然后在每次迭代中对所选特征子集应用K-均值。重复此过程，直到达到选定特征子集的散布轨迹标准的最高值。

另一种混合双向特征选择方法（Yun Li et al.2006）首先尝试使用基于熵的度量和模糊评价指数（FFIE）消除冗余特征（Pal et al.2000）。在冗余特征消除阶段之后，利用FCM和散射跟踪准则，从缩减后的特征集中选择一个最优的特征子集。然而，没有进行全面的实验分析来评估混合包装滤波器方法的性能。

Solorio Fernández等人（2016年）提出了一种基于拉普拉斯分数（He等人2005年）和卡林斯基-哈拉巴斯指数（卡林斯基和哈拉巴斯1974年）的混合两阶段方法。在第一阶段，使用拉普拉斯评分对数据中的特征进行排序。在第二阶段中，对通过正向和反向策略获得的选定特征子集应用K-均值来生成聚类集，然后使用称为加权归一化Calinski–Harabasz指数（WNCH）的Calinkski-Harasz改进版本对生成的聚类集进行评估。在可能的特征子集中，选择WNCH值最高的特征子集作为最优特征子集。

Jaskhi等人（2009）介绍了一种用于文档聚类的包装过滤器方法。该方法首先使用随机标签随机标记文档。然后使用贝叶斯模型选择特征子集。在最后一步中，对选定的特征子集应用K-means。重复此步骤，直到满足停止标准。另一种wrapper-filter方法（Kim et al.2006）试图通过应用最小平方估计（LSE）准则（Mao 2005）来找到大量特征，然后应用期望最大化算法的改进版本来选择最大程度提高聚类性能的最佳特征子集。

Hruschka等人（2005年）介绍了一种包装过滤器特征选择方法（BFK），它结合了K-均值和贝叶斯网络。与之前的包装过滤器方法不同，BFK首先通过对一系列集群应用K均值来执行包装阶段。下一阶段选择轮廓指数最高的集群结构（Rousseeuw 1987）。换句话说，使用传统的方法，簇结构是自动演化的，而不需要k个簇。在过滤阶段，借助贝叶斯网络选择特征子集，将每个聚类和特征分别视为一个类和一个节点。尽管与以前的包装过滤器方法相比，它可以被视为一种新的包装过滤器方法，但其性能在很大程度上取决于轮廓索引。例如，如果没有使用轮廓索引正确确定簇结构，则特征选择的进一步过滤过程将受到不利影响。有关针对聚类提出的更多包装过滤器方法，请参见（Yang等人2011；Zhang等人2012；Fan等人2013）。

4 Furtherdiscussions

4.1 Summary of studies

本节的主要重点是对聚类的特征选择进行概述和讨论。从提出的用于聚类的特征选择方法可以发现，特征选择的主要目标是提高聚类质量、减少存储需求和提高时间计算效率。然而，现有工作仍存在各种局限性，例如需要预先定义聚类数、特征数或具有少量聚类的数据，或者对高维数据集的分析不足。如何将特征选择应用于聚类仍然是一个悬而未决的问题，尚未得到充分解决。

特征选择过程应该在聚类过程之前还是之后？

或者，特征选择和聚类应该同时执行还是同步执行？

我们将使用哪种方法进行聚类取决于集群结构是否被保留。

如果在聚类之前应用了特征选择，则首先从整个数据中选择特征子集，然后在所选特征空间上应用聚类。换句话说，特征选择过程独立于聚类过程。本文在滤波器特征选择方法中考虑了这种方法。过滤方法可以很容易地应用于监督和非监督学习任务。这些方法的目的是建立一个亲和力/相似性矩阵，然后获得每个特征的分数。尽管这些方法简单明了，但这些方法无法处理特征冗余，因为它们在特征选择过程中反复倾向于选择高度相关的特征。

在第二种方法中，特征选择与聚类同步执行。因此，所选特征子集取决于聚类算法。在特征选择术语中，这种方式通常被称为包装器。在这项工作中，包装器分为三组：K-means的特征选择、基于模型的特征选择和基于EC的聚类算法的特征选择。由于K-means算法被认为是研究人员最常用的聚类算法之一，因此人们提出了大量的工作来提高K-means算法的聚类性能。该问题的一个解决方案是将特征加权方案集成到K-means算法中。通过这种方法，通过去除数据中的无关、冗余和弱冗余特征来提高K-means的聚类性能。文献中提出了多种用于K-均值的特征加权方法。根据结果，它们显著提高了K-means算法的性能。然而，它们仍然面临一些挑战：初始条件、预定义参数的依赖性以及过早收敛到局部最优。此外，我们观察到大量关于K-means特征选择的研究没有引入全面的实验研究。例如，在Chan et al.（2004）、Tsai和Chiu（2008）中，实验研究只使用了两到三个真实世界的基准。另一个例子是，Amorim等人（2013年）在各种基准数据集中介绍了K-均值特征选择方法的综合比较研究。然而，实验中没有给出纯K-均值算法的结果。对于特征权重如何影响K-means的性能，它缺乏一致的分析。

另一类包装器，与K-means的特征选择方法相比，基于模型的聚类的特征选择方法不需要额外的预定义参数。另一方面，它们只能检测高斯分布的簇，也就是说，它们不能正确地检测未定型或均匀分布的簇。因此，在实际数据集上可能无法获得最佳的聚类性能，这些数据集大多以不定型分布的形式存在。

最后一类包装是为进化聚类提出的特征选择方法。我们研究了基于目标数量的进化聚类特征选择方法。对于单目标方法，最常见的方法是允许同时进行特征选择和聚类过程。具体而言，这些方法试图优化聚类性能和可能选择的特征子集的特征子集大小。尽管这些方法能够在数据中找到分离良好的聚类，但由于对少数聚类存在偏差问题，因此，数据中的所有特征，而不仅仅是选定的特征，都被认为是衡量聚类性能的指标。换句话说，通过选定的特征子集无法正确评估簇的质量。单目标特征选择方法的另一种方法是在进化过程中应用局部添加-删除算子（添加和/或删除特征）。这种方法不像以前的方法那样常见，但是只使用选定的特征来评估集群性能。然而，使用本地add-remove操作符的方法无法达到令人满意的集群性能。在考虑多目标方法时，与大多数单目标方法一样，不存在导致聚类和特征选择之间存在偏差问题的挑战，即，所选特征集的聚类性能可以在没有任何要求的情况下进行评估。然而，从帕累托前沿选择哪种解决方案是一项具有挑战性的任务。为了解决这个问题，一个半监督选择方案被应用于少量的解决方案。此外，与单目标方法相比，多目标方法的研究最近才开始考虑，并且仍处于初级阶段。

在特征选择与聚类同步应用的情况下，嵌入式方法也发挥了重要作用，特别是在最近几年。下面给出了嵌入式方法的两种通用工作方案。在第一种方案中，首先使用聚类算法获得伪聚类标签，然后使用生成的标签将无监督特征选择转化为有监督的概念。换句话说，簇标签被视为类标签，以便执行特征选择。如果生成的簇（即簇标签）不是真实的或最优的簇，则特征选择过程很难获得好的结果。在第二种方案中，特征选择直接用于聚类，而不需要转换。与第一种方案相比，第二种方案在具有大幅度特征的数据集中工作良好。这两种方案都是使用稀疏学习方法的原理构建的。尽管基于嵌入式稀疏学习的特征选择方法已经取得了很好的效果，但是这些方法仍然存在一些挑战：复杂的矩阵运算和密集的计算开销。此外，在文献中，围绕该方案的特征选择方法很少。请注意，一些基于稀疏学习的特征选择方法（例如SPEC）可以在过滤器类别中进行评估。

本研究考虑的最后一种方法是在一个框架中混合包装器和过滤器。虽然混合方法被认为可以提高学习算法的有效性和效率，但与包装器和过滤器相比，它们在文献中并不常见。构建混合包装过滤器模型最常用的方法是双向混合方法，该方法首先使用过滤器方法来降低维度，然后在降低的特征集上应用包装方法来找到更合适的特征子集。根据文献中的各种研究，双向方法已经在聚类方面取得了有希望的结果。然而，在双向方法中，两个阶段之间没有相互作用，即两个阶段独立地执行其过程。因此，需要同步组合包装器和过滤器阶段的混合包装器过滤器方法。这个问题的一个解决方案是将本地搜索过滤器（wrapper）机制集成到wrapper（filter）框架中。在提出分类的文献中，存在一些使用局部搜索机制将包装和过滤阶段相结合的包装过滤器方法（Hancer 2019；Butler-Yeoman等人，2015），但开发此类用于聚类的包装过滤器方法仍然是一个悬而未决的问题。

4.2 Future trends

已有许多特征选择算法被提出用于聚类，虽然取得了一定的成功，但也存在局限性。特征选择本身是一项具有挑战性的任务，由于缺少实例的目标标签，无监督的特征选择更加困难。在这一领域，如可扩展性、速度和评估措施等，还有许多有待进一步研究的空间。随着数据集规模的巨大增长，当前聚类算法的可伸缩性可能成为一个大问题。为聚类而提出的特征选择方法也面临类似的问题。然而，大多数聚类方法需要将所有特征保留在内存中，以观察聚类结构中的任何变化。如果在数据结构中观察到任何差异，则应重新启动聚类过程。此外，特征选择方法的可伸缩性是一个大问题。特征选择方法通常需要足够数量的数据实例来获得良好的学习性能。为了解决这个问题，有些方法只记住重要的实例或原型，即每个集群的平均值。因此，聚类和特征选择方法的可扩展性应该更加关注，以跟上数据的增长和快速流化。

在大多数数据挖掘任务中，计算时间通常是一个大问题，即使对于中等大小的数据集也是如此。特征选择具有较大的搜索空间，搜索空间随数据集中原始特征的数量呈指数增长。用于聚类的特征选择，尤其是包装方法，成本非常高，主要是因为每次评估都需要执行聚类过程来测试所选特征子集的优劣。当数据集大小较大时，此过程会变得更慢。虽然用于聚类的特征选择可以减少未来应用程序的计算时间，但选择特征本身的过程需要加快。这可以通过开发一种有效的特征选择搜索机制，或一种快速过滤无用特征的两阶段方法，或快速评估措施来实现。

评价指标是决定特征选择和聚类的速度和最终性能的重要因素。聚类作为一种无监督的方法比分类更难，在分类中，训练集有学习算法的基本真理类标签，并且性能度量很容易确定，例如精度或F度量。有许多可用的聚类评估度量，例如，各种簇内或簇间距离、紧凑性、分离性和连通性。还有内部措施和外部措施。然而，对于同一组聚类结果，不同的评价指标往往表现出不同的优度水平，并建议使用不同的方法作为最佳算法。因此，用户很难做出决定。制定强有力的综合评估措施是一项非常具有挑战性的任务，但将极大地造福于社区。

5 Conclusions

在本文中，我们介绍了一个全面的调查特征选择方法聚类。为了更好地总结这个领域的概况，我们引入了一个简单的评估分类，即过滤方法、包装方法、嵌入方法和混合方法。此外，包装器被进一步分类为基于K-means、基于模型和基于进化聚类的算法。基于这一分类，我们详细讨论了相应的工作，包括它们的关键思想、结果和局限性。本文的另一个贡献是深入讨论了进化聚类的特征选择方法。据我们所知，目前还没有专门针对进化聚类设计的特征选择方法的研究。我们还讨论了该领域未来可能的趋势和挑战，如可伸缩性、算法的速度以及聚类特征选择中的强大评估措施。