5 MLP版本的鸢尾花分类任务

MLP-多层感知机
一次线性变化加上一次激活函数组成MLP中完整的一个隐藏层，又称全连接层( Dense Layer )。
此版本为3个全连接层的鸢尾花分类模型
主代码模块如下：

import numpy as np
import torch
from torch import nn
from torch.utils.data import DataLoader
from chapter1 import data_download_and_load as ddal  # 数据下载
import matplotlib.pyplot as plt
import tqdm  # 进度条模块


# 画散点图
def draw_scatter(ds, names):
    fig, ax = plt.subplots()
    x = range(len(ds[0]))
    for d, name in zip(ds, names):
        ax.scatter(x, d, alpha=0.6, label=name)
        ax.legend(fontsize=16, loc='upper left')
        ax.grid(c='gray')
    plt.show()


# 计算精度
def accuracy4classification(true_classes, pr_classes):
    return sum(np.array(true_classes) == np.array(pr_classes))/len(true_classes)


# 多层感知机版本
class SoftmaxRegMLP(nn.Module):

    # 初始化子类
    def __init__(self, n_features, n_classes):

        # 继承父类属性
        super(SoftmaxRegMLP, self).__init__()  # 第一种继承方法 python2 python3通用
        # 初始化权值
        self.mlp = nn.Sequential(
            nn.Linear(n_features, n_features * 2),  # 初始化线性层 输入特征数量 输出类别数量
            nn.Sigmoid(),  # 激活函数 使形成一个完整的隐藏层 又称全连接层
            nn.Linear(n_features * 2, n_features),
            nn.Sigmoid(),
            nn.Linear(n_features, n_classes),
            nn.Softmax(dim=1),  # Softmax激活函数常用于多分类中
        )

    # 前向传播
    def forward(self, x):
        y = self.mlp(x)  # MLP多层感知机网络
        return y


@torch.no_grad()  # 关掉梯度计算 节省计算时间
def eva(dates, net):

    net.eval()  # 测试模式
    x = torch.Tensor(dates[:, :-1])  # 将测试集数据转化为tensor格式
    y = dates[:, -1]
    y_pr = net.forward(x)  # 输入必须为tensor格式

    pr_classes = np.argmax(y_pr, axis=1)  # 取矩阵里各项最大值的索引 对应标签值
    acc = accuracy4classification(y, pr_classes)  # 计算精度

    return acc


def train(epochs=100, batch_size=8, lr=0.01):

    # 数据处理
    df = ddal.load_iris()  # 下载数据 为csv格式（float32） 这里不需要归一化
    n_features = df.shape[1] - 1  # 权重项个数
    n_classes = len(df["target"].unique())  # unique去重获取标签的类别数
    train_df, test_df = ddal.split_train_test_from_df(df, test_ratio=0.2)  # 将数据集划分为训练集和测试集

    # 初始化模型、损失函数、梯度下降函数三大类
    net = SoftmaxRegMLP(n_features, n_classes)  # 初始化模型 同时初始化权值
    criterion = nn.CrossEntropyLoss()  # 初始化交叉熵损失函数 常用于多分类与二分类问题
    optimizer = torch.optim.AdamW(net.parameters(), lr=lr)  # 初始化梯度下降函数

    net.train()  # 训练模式
    for e in range(epochs):
        for datas in DataLoader(train_df.values, batch_size=batch_size, shuffle=True):
            optimizer.zero_grad()  # 梯度归0
            x = datas[:, :-1]  # 获取X 训练值
            y = torch.LongTensor(datas[:, -1].detach().numpy())  # 获取y 这里是真值为类别代码 需要将数据转换为tensor格式的long类型
            y_pr = net.forward(x)  # 得到预测值y 这里返回的一个带有概率值的一维矩阵 如[0.2, 0.5, 0.3]
            loss = criterion(y_pr, y)  # 将预测的y与真实的y带入损失函数计算损失值 注意这里第一个参数需要是概率值即网络的最后一层输出 第二个参数需要是标签的索引值
            loss.backward()  # 后向传播 从输出根据链式求导法则求损失函数对于各个模型参数的偏导，以更新各模型参数的过程
            optimizer.step()  # 沿梯度下降方向更新所有参数

    # 测试训练结果
    return eva(test_df.values, net)


if __name__ == '__main__':
    a = []
    for i in tqdm.tqdm(range(100)):  # 将总的训练时常分为100份
        acc = train()
        a.append(acc)
    print(np.average(np.array(a)))

from chapter1 import data_download_and_load as ddal  # 数据下载

代码模块如下：

import pandas as pd  # 科学计算库 数据基本结构为DataFrame
from sklearn import datasets  # 机器学习库
from data_set import filepaths as fp
from os import path as osp
import numpy as np
from utils import osUtils as oU
import random


BOSTON_CSV = osp.join(fp.BOSTON_DIR, 'boston.csv')
IRIS_CSV = osp.join(fp.IRIS_DIR, 'iris.csv')
ML100K_TSV = osp.join(fp.ML100K_DIR, 'rating_index.tsv')


# 将下载的数据转化为DataFrame格式（pandas所用的格式）
def sklearn_to_df(sklearn_dataset):
    df = pd.DataFrame(sklearn_dataset.data, columns=sklearn_dataset.feature_names)
    df['target'] = pd.Series(sklearn_dataset.target)
    return df


# 下载波士顿房价数据及格式转换
def download_boston():
    boston = datasets.load_boston()  # 从datasets数据库里下载波士顿房价数据
    df = sklearn_to_df(boston)  # 将下载的数据转化为DataFrame格式（pandas所用的格式）
    print(df)
    df.to_csv(BOSTON_CSV)  # 将DataFrame格式转化为excel可读的csv格式


# 读取波士顿房价csv文件并转化为pandas所用的DataFrame格式
def load_boston():
    return pd.read_csv(BOSTON_CSV, index_col=0, dtype=np.float32)


# 下载鸢尾花数据及格式转化
def download_iris():
    iris = datasets.load_iris()
    df = sklearn_to_df(iris)
    df.to_csv(IRIS_CSV)


# # 读取鸢尾花csv文件并转化为pandas所用的DataFrame格式
def load_iris():
    return pd.read_csv(IRIS_CSV, index_col=0, dtype=np.float32)


# 将数据划为为训练集和测试集
def split_train_test_from_df(df, test_ratio=0.2):  # 指定测试集的百分比
    test_df = df.sample(frac=test_ratio)  # 在数据集里面采样20%作为测试集
    train_df = df[~df.index.isin(test_df.index)]  # 其余的为训练集
    return train_df, test_df


def read_rec_data(path=ML100K_TSV, test_ratio=0.2):
    user_set, item_set = set(), set()
    triples = []
    for u, i, r in oU.readTriple(path):
        user_set.add(int(u))
        item_set.add(int(i))
        triples.append((int(u), int(i), int(r)))

    test_set = random.sample(triples, int(len(triples)*test_ratio))
    train_set = list(set(triples)-set(test_set))

    # 返回用户集合列表，物品集合列表，与用户，物品，评分三元组列表
    return list(user_set), list(item_set), train_set, test_set


if __name__ == '__main__':
    download_boston()

数据集一共150条训练数据，训练集：测试集=4：1，共3个分类
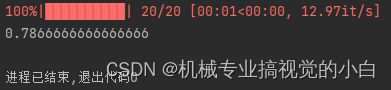
训练了20个epoch，batch_size = 8, lr = 0.01
单层网络训练结果如下：

多层网络训练结果如下：

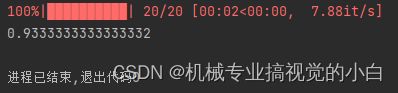
可以看出，明显在多层网络下的效果要比单层网络效果好，不过相应的多层网络下训练的时间也会随之增长。