ComSec作业二:AES
文章目录
- 前言
- 一、描述AES中S-Box的生成过程
- 二、证明公式6.9与公式6.4等价
- 三、写一个GF(2^8)的乘法函数Mul
- 四、写一个程序,生成AES算法中的S-Box
- 总结
前言
AES 是密码学中的高级加密标准,又称Rijndael加密法,是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES,它能抵抗所有已知的攻击,且在各平台上易于实现,速度快;设计简单。
一、描述AES中S-Box的生成过程
初始化 S-box
将 S-Box中的值映射成其乘法逆元B【运用扩展欧几里得算法】
用第 2 步的结果做仿射变换 【{63} 记为C】
B' = X*B ⊕ {63}
具体求解步骤如下:(0001 1111)
这里以第B行第2列元素{B2}为例
(1)求16进制数 {B2} 在有限域 GF( 2 8 2^8 28) 上的逆元:
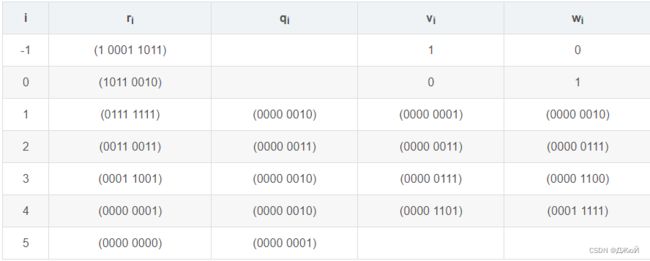
从表中得到 (0000 1101) * (1 0001 1011) + (0001 1111) * (1011 0010) = 1
所以 (0001 1111),即{1F},是{B2}在有限域 GF( 2 8 2^8 28) 上的逆元
(2)用 {1F} 做仿射变换
B = {1F} = 0001 1111
= b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 b_7b_6b_5b_4b_3b_2b_1b_0 b7b6b5b4b3b2b1b0
C = {63} = 0110 0011
= c 7 c 6 c 5 c 4 c 3 c 2 c 1 c 0 c_7c_6c_5c_4c_3c_2c_1c_0 c7c6c5c4c3c2c1c0
B’ = b 7 ′ b 6 ′ b 5 ′ b 4 ′ b 3 ′ b 2 ′ b 1 ′ b 0 ′ b'_7b'_6b'_5b'_4b'_3b'_2b'_1b'_0 b7′b6′b5′b4′b3′b2′b1′b0′
由仿射变换定义:
b 0 ′ b'_0 b0′ = b 0 ⊕ b 4 ⊕ b 5 ⊕ b 6 ⊕ b 7 ⊕ c 0 b_0⊕ b_4⊕ b_5⊕ b_6⊕ b_7⊕c_0 b0⊕b4⊕b5⊕b6⊕b7⊕c0 = 1
b 1 ′ b'_1 b1′ = b 1 ⊕ b 5 ⊕ b 6 ⊕ b 7 ⊕ b 0 ⊕ c 1 b_1⊕ b_5⊕ b_6⊕ b_7⊕ b_0⊕c_1 b1⊕b5⊕b6⊕b7⊕b0⊕c1 = 1
b 2 ′ b'_2 b2′ = b 2 ⊕ b 6 ⊕ b 7 ⊕ b 0 ⊕ b 1 ⊕ c 2 b_2⊕ b_6⊕ b_7⊕ b_0⊕ b_1⊕c_2 b2⊕b6⊕b7⊕b0⊕b1⊕c2 = 1
b 3 ′ b'_3 b3′ = b 3 ⊕ b 7 ⊕ b 0 ⊕ b 1 ⊕ b 2 ⊕ c 3 b_3⊕ b_7⊕ b_0⊕ b_1⊕ b_2⊕c_3 b3⊕b7⊕b0⊕b1⊕b2⊕c3 = 0
b 4 ′ b'_4 b4′ = b 4 ⊕ b 0 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 4 b_4⊕ b_0⊕ b_1⊕ b_2⊕ b_3⊕c_4 b4⊕b0⊕b1⊕b2⊕b3⊕c4 = 1
b 5 ′ b'_5 b5′ = b 5 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ b 4 ⊕ c 5 b_5⊕ b_1⊕ b_2⊕ b_3⊕ b_4⊕c_5 b5⊕b1⊕b2⊕b3⊕b4⊕c5 = 1
b 6 ′ b'_6 b6′ = b 6 ⊕ b 2 ⊕ b 3 ⊕ b 4 ⊕ b 5 ⊕ c 6 b_6⊕ b_2⊕ b_3⊕ b_4⊕ b_5⊕c_6 b6⊕b2⊕b3⊕b4⊕b5⊕c6 = 0
b 7 ′ b'_7 b7′ = b 7 ⊕ b 3 ⊕ b 4 ⊕ b 5 ⊕ b 6 ⊕ c 7 b_7⊕ b_3⊕ b_4⊕ b_5⊕ b_6⊕c_7 b7⊕b3⊕b4⊕b5⊕b6⊕c7 = 0
所以 B’ = 0011 0111 = {37}
因此,在S-Box中,第B行第2列对应 的值为{37}。
以此类推,即可求出其他位置的对应值
注意:0无逆元,S-box的构造规则要求{00}映射到其本身

二、证明公式6.9与公式6.4等价

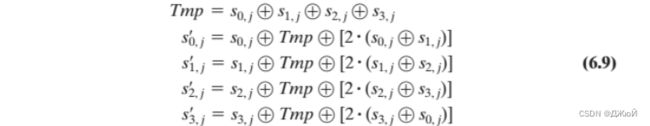
解: S 0 , j ′ = S'_{0,j} = S0,j′= S 0 , j ⊕ T m p ⊕ [ 2 • ( S 0 , j ⊕ S 1 , j ) ] S_{0,j} ⊕ Tmp ⊕[2 •(S_{0,j} ⊕S_{1,j} )] S0,j⊕Tmp⊕[2•(S0,j⊕S1,j)]
= S 0 , j ⊕ S 0 , j ⊕ S 1 , j ⊕ S 2 , j ⊕ S 3 , j ⊕ [ 2 • ( S 0 , j ⊕ S 1 , j ) ] =S_{0,j} ⊕ S_{0,j} ⊕S_{1,j} ⊕S_{2,j} ⊕S_{3,j}⊕[2 •(S_{0,j} ⊕S_{1,j} )] =S0,j⊕S0,j⊕S1,j⊕S2,j⊕S3,j⊕[2•(S0,j⊕S1,j)]
= S 1 , j ⊕ S 2 , j ⊕ S 3 , j ⊕ ( 2 • S 0 , j ) ⊕ ( 2 • S 1 , j ) =S_{1,j} ⊕S_{2,j} ⊕S_{3,j}⊕(2 •S_{0,j} ) ⊕(2 •S_{1,j} ) =S1,j⊕S2,j⊕S3,j⊕(2•S0,j)⊕(2•S1,j)
= ( 2 • S 0 , j ) ⊕ ( 3 • S 1 , j ) ⊕ S 2 , j ⊕ S 3 , j =(2 •S_{0,j} ) ⊕(3 •S_{1,j} ) ⊕S_{2,j} ⊕S_{3,j} =(2•S0,j)⊕(3•S1,j)⊕S2,j⊕S3,j
同理可证得其他三项
所以说,公式 6.9 与 公式 6.4 等价
三、写一个GF(2^8)的乘法函数Mul
写一个 GF( 2 8 2^8 28) 的乘法函数Mul,输入 GF( 2 8 2^8 28) 的两个元素 a、b,输出a * b 。
提示:回忆 CINTA 的 Simple Multiplication。
#include- 原理:
在二进制中,所有的数都能用0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80异或得到 - 预处理:
对于 a 本身,依次乘以以上8个数,得到8个预知结果 - 结果:
根据 b 把上面预知的结果异或起来,即可得到 a*b 的结果
四、写一个程序,生成AES算法中的S-Box
#include
总结
通过本章的学习,掌握了 GF( 2 8 2^8 28) 内的各种运算操作,以及AES中S-Box的生成
有限域GF(2^8)内乘法代码实现以及原理