Python机器学习日记（七）

 支持向量机SVM的核函数

在SVM算法中，徐连模型的过程实际上是对每个数据点对于数据分类决定边界的重要性进行判断。在训练数据集中，只有一部分数据对于边界的确定是有帮助的，这些数据被称为“支持向量”

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

X,y = make_blobs(n_samples=50,centers=2,random_state=6)

clf = svm.SVC(kernel='linear',C=1000)
clf.fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0],xlim[1],30)
yy = np.linspace(ylim[0],ylim[1],30)
YY,XX = np.meshgrid(yy,xx)
xy= np.vstack([XX.ravel(),YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)

ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
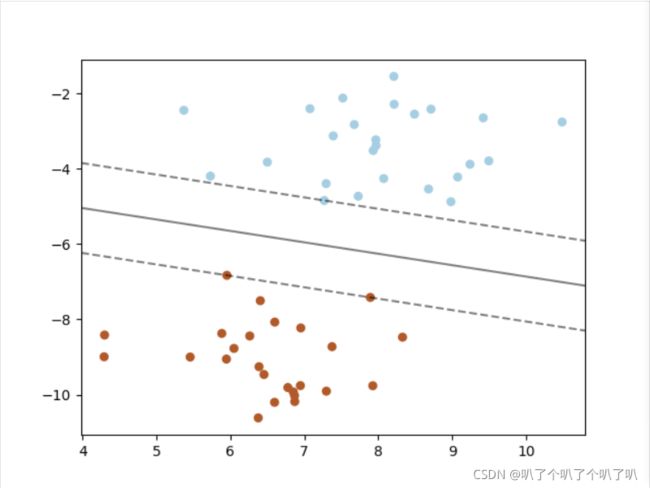
ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100,linewidth=1,facecolors='none')
plt.show()

 在分类器两侧分别有两条虚线，那些正好压在虚线上的点，就是支持向量。学不动了，溜了

---

接下来我们将SVM的内核换成是RBF，就可以得到不同的分类器形状。

接下来看一下不同核函数的SVM对比。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.datasets import load_wine

def make_meshgrid(x,y,h=.02):
    x_min,x_max = x.min() - 1,x.max()+1
    y_min,y_max = y.min() -1 ,y.max()+1
    xx,yy = np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
    return xx,yy
#定义一个函数用来画图

def plot_contours(ax,clf,xx,yy,**params):
    Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx,yy,Z,**params)
    return out
#定义一个绘制等高线的函数

wine = load_wine()
X = wine.data[:,:2]
y = wine.target

C = 1.0 #SVM的正则化函数
models = (svm.SVC(kernel='linear',C=C),
          svm.LinearSVC(C=C),
          svm.SVC(kernel='rbf',gamma=0.7,C=C),
          svm.SVC(kernel='poly',degree=3,C=C))

models=(clf.fit(X,y) for clf in models)

#设定图题
titles = ('SVC with linear kernel',
          'LinearSVC(linear kernel),'
          'SVC with RBF kernel',
          'SVC with polynomial (degree 3) kernel')

#设一个子图形的个数和排列方式
fig,sub = plt.subplots(2,2)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
#使用前面定义的函数进行画图
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)

for clf,title,ax in zip(models,titles,sub.flatten()):
    plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
    ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors='k')
    ax.set_xlim(xx.min(),xx.max())
    ax.set_ylim(yy.min(),yy.max())
    ax.set_xlabel('Feature 0')
    ax.set_ylabel('Feature 1')
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)

plt.show()

出现了错误 

ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  warnings.warn("Liblinear failed to converge, increase "

查了一下好像是max值不够大影响美观，但是还没有找到解决办法

 从图中我们可以看到线性内核SVC与linearSVC得到的结果非常近似，他们的决定边界都是线性的，而RBF内核的SVC的决定边界则不完全是线性的，更佳的弹性。决定了边界形状的就是参数C，接下来重点观察一下RBF内核SVM的gamma参数调节。

models =(svm.SVC(kernel='rbf',gamma=0.1,C=C),
          svm.SVC(kernel='rbf',gamma=1,C=C),
          svm.SVC(kernel='rbf',gamma=10,C=C))

models=(clf.fit(X,y) for clf in models)

titles = ('gamma = 0.1',
          'gamma = 1',
          'gamma = 10',)

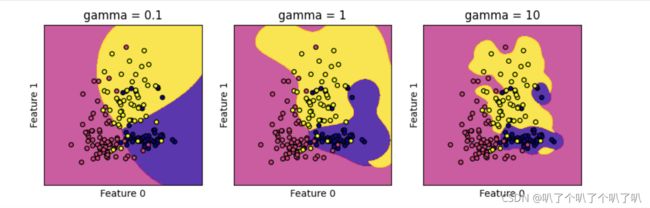
fig,sub = plt.subplots(1,3,figsize = (10,3))

 gamma值越小，RBF内核的直径就越大，可以将更多的点被模型圈进决定边界中，所以决定边界也就越平滑，知识的模型也就越简单；随之参数的增加，模型更倾向于把每一个点都放到相应的决定边界中。故gamma值越小，模型越倾向于欠拟合，反之亦然。

SVM还是在图像识别领域以及样本特征数和样本数比较接近的时候才会比较得心应手

---

SVM实例----波士顿房价回归预测

首先先了解一下数据集的大致情况

from sklearn.datasets import load_boston
boston = load_boston()
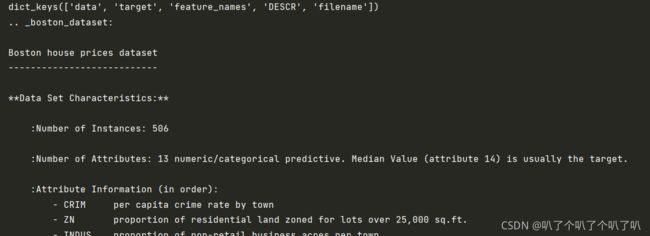
print(boston.keys())
print(boston['DESCR'])

 先制作训练数据集和测试数据集

X,y = boston.data,boston.target
X_train,X_test,y_train,y_tset = train_test_split(X,y,random_state=8)
print('\n\n\n')
print('代码运行结果')
print(X_train.shape)
print(X_test.shape)

 

 然后用SVR进行建模，分别尝试Linear和rbf

for kernel in ['linear','rbf']:
    svr = SVR(kernel=kernel)
    svr.fit(X_train,y_train)
    print(kernel,'核函数的模型训练集得分：{:.3f}'.format(svr.score(X_train,y_train)))
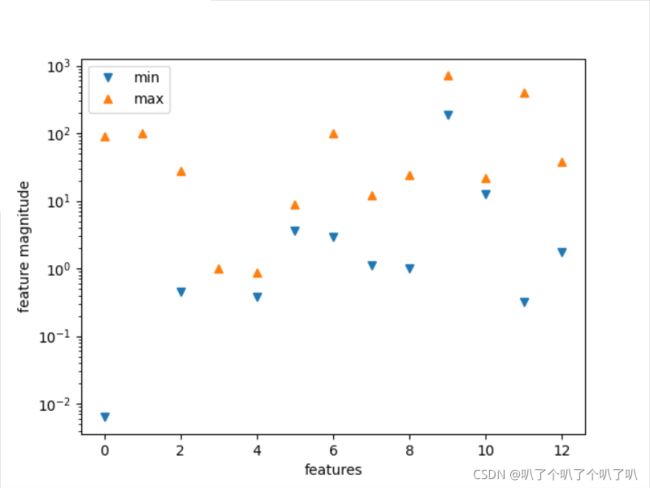
    print(kernel,'核函数的模型训练集得分：{:.3f}'.format(svr.score(X_test, y_test)))

 明显可以看到rbf核函数的得分是非常糟糕的，这是因为SVM算法对数据的预处理的要求是很高的，如果数据特征量级差异较大，就需要对数据进行预处理。接线来用图形可视化来检查一下特征的数量级。

#将特征值中的最小值和最大值用散点画出来
plt.plot(X.min(axis=0),'v',label='min')
plt.plot(X.max(axis=0),'^',label='max')
#设定纵坐标为对数形式
plt.yscale('log')
#设置图注位置为最佳
plt.legend(loc='best')
#设定横纵轴标题
plt.xlabel('features')
plt.ylabel('feature magnitude')
#显示图形
plt.show()

 特征值的范围在10^-2到10^2，范围很大，需要对数据集进行预处理

scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
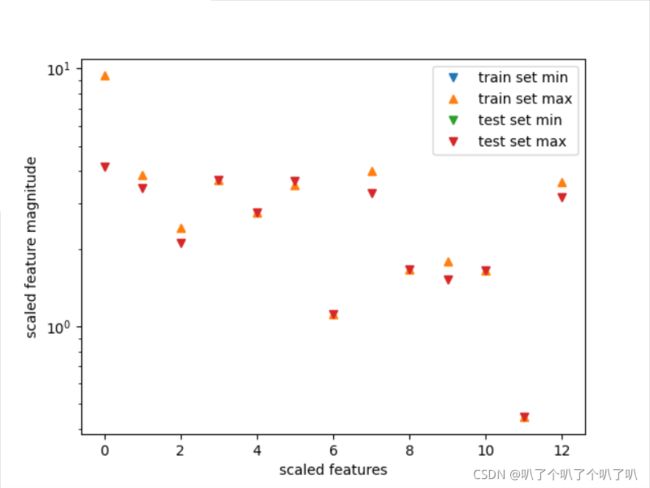
#将预处理的数据特征最大值和最小值用散点图表示出来
plt.plot(X_train_scaled.min(axis=0),'v',label='train set min')
plt.plot(X_train_scaled.max(axis=0),'^',label='train set max')
plt.plot(X_test_scaled.min(axis=0),'v',label='test set min')
plt.plot(X_test_scaled.max(axis=0),'v',label='test set max')
plt.yscale('log')

#设置图注位置
plt.legend(loc='best')

#设置横纵轴标题
plt.xlabel('scaled features')
plt.ylabel('scaled feature magnitude')
plt.show()

 经过预处理之后，训练集和测试集的最大特征值都不会超过10，接下来用经过预处理的数据来训练模型。

进一步调整gamma和C两个参数

svr = SVR(C=100,gamma=0.1)
svr.fit(X_train_scaled,y_train)
print('调整参数后的模型在训练集得分：{:.3f}'.format(svr.score(X_train_scaled,y_train)))
print('调整参数后的模型在测试集得分：{:.3f}'.format(svr.score(X_test_scaled,y_test)))

 

得到很好的一个分数。 

SVM的一般流程：

1.收集数据

2.准备数据：需要数值型数据

3.分析数据：有助于可视化分隔超平面

4.训练算法

5.测试算法

6.使用算法

---

Platt的SMO算法

SMO用来训练SVM，表示序列最小化。将大优化问题分成多个小优化问题来求解。

接下来看一下简化版的SMO算法 ，首先是SMO中的辅助函数

from numpy import *


def loadDataSet(filename):
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split(" ")
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

def selectJrand(i,m):
    j=i
    while(j==i):
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    if aj>H:
        aj=H
    if L>aj:
        aj = L
    return aj

dataArr,lableArr = loadDataSet('F:\python\machinelearninginaction\Ch02\\testSet.txt')
print(lableArr)

出现报错： 

 could not convert string to float: ' '

不能将' '转换成浮点型数据，将split(" ")转换成split()问题解决，在默认没有参数的情况下可以删除其他符号，而有参数的情况下只能删除占位符。

伪代码大致如下：

创建一个aplha向量并将其初始化为0向量
当迭代次数小于最大迭代次数时（外循环）：
    对数据集中的每个数据向量（内循环）：
       如果该数据向量可以被优化：
             随机选择另外一个数据向量
             同时优化这两个向量
             如果两个向量都不能被优化，退出内循环
如果所有向量都没被优化，增加迭代数目，继续下一次循环。 

def smoSimple(dataMathIn, classLabels, C, toler, maxIter):
    # 有5个输入参数，分别是：数据集、类别标签、常数C、容错率和退出前最大的循环次数
    dataMatrix = mat(dataMathIn)
    labelMat = mat(classLabels).transpose()
    # 将输入空间矩阵化
    b = 0
    m, n = shape(dataMatrix)
    # 通过矩阵dataMatrix的shape属性得到常数m,n
    alphas = mat(zeros((m, 1)))
    iter = 0
    # 建立一个列矩阵，矩阵中元素都初始化为0，并建立一个iter变量，该变量存储的是在没有任何alpha改变的情况下\
    # 遍历数据集的次数
    while (iter < maxIter):
        alphaPairsChanged = 0
        # 对整个集合进行顺序遍历，变量alphaPairsChanged用于记录alpha是否已经进行优化
        for i in range(m):
            # 将问题转化为 二阶问题 抽取alphas[i]，alphas[j] 进行优化
            fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            # 预测的类别
            Ei = fXi - float(labelMat[i])
            # 基于这个实例的预测结果和真实结果计算误差Ei
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler)) \
                    and (alphas[i] > 0):
                # 如果误差很大则进入优化过程，不管是正间隔还是负间隔都会被测试，同时保证alpha的值不能等于0或C
                # 如果alpha<0||>C,将被调整为0或C，所以如果if语句中等于这两个值，就已经在“边界”了
                # 也就是不再值得再对它们进行优化
                j = selectJrand(i, m)
                # 使用辅助函数来随机选择第二个alpha的值
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 通过copy()的方法来实现alpha的误差
                # 要为这两个分配新的内存，否则在对新值和旧值进行比较时，我们就看不到新旧值的变化
                if labelMat[i] != labelMat[j]:
                    L = max(0, alphas[j] - alphas[i] - C)
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, C + alphas[j] + alphas[i])
                # 保证alpha的值在0和C之间
                if L == H:
                    print("L==H")
                    continue
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] \
                      * dataMatrix[i, :].T - dataMatrix[j, :] * dataMatrix[j, :].T
                # eta是alpha[j]的最优修改量，如果为0则需要退出for循环的当前迭代过程
                if eta >= 0:
                    print("eta>=0")
                    continue
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                alphas[j] = clipAlpha(alphas[j], H, L)
                # 如果eta为0，计算新的alpha[j]，并用辅助函数对L,H的值进行调整
                if abs(alphas[j] - alphaJold < 0.00001):
                    print("j not moving enough")
                    continue
                    # 检查alpha[j]的值是否有轻微改变，如果有则退出循环
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] \
                     * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] \
                     * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] \
                     * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alphaJold) * \
                     dataMatrix[j, :] * dataMatrix[j, :].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                # 如果两个值同样进行改变但改变的方向正好相反，那么在对其进行优化后，给他们设置一个常数项b
                alphaPairsChanged += 1
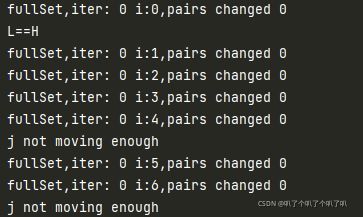
                print("iter :%d i:%d,pairs changed %d" % (iter, i, alphaPairsChanged))
            if alphaPairsChanged == 0:
                iter += 1
            else:
                iter = 0
            print("iteration number:%d" % iter)
            #如果for循环结束都没有执行continue语句，那么就成功的改变了一堆alpha，同时可以增加
            #alphaPairsChanged的值，在for循环外检查alpha的值是否作了更新，如果有则将iter设为0后继续运行程序。
            #只有在所有数据集上遍历maxIter次，且不再发生任何alpha修改之后，程序才会停止并退出while循环
        return b, alphas
    # 当变量达到输入值maxIter时，函数结束运行并退出。

这个函数比较长，接下来慢慢学习。

利用完整Platt SMO算法加速优化

在几百个点组成的小规模数据集上简化版SMO算法的运行是没有什么问题的，但在更大的数据集上的运行速度就会变慢。两个程序唯一不同的就是alpha的方式。

Platt SMO算法是通过一个外循环来选择第一个alpha值得，并且其选择过程会在两种方式之间进行交替：一种是在所有数据集上进行单遍扫描，另一中是在非边界alpha中实现单遍扫描。

要对上述代码进行改进和清理，在优化过程中通过最大化步长的方式来获得第二个alpha的值，建立一个全局的缓存用于保存误差值，并从中选择是的步长或Ei-Ej最大的alpha的值。

class optStruct:
    def __int__(self,dataMatIn,classLabels,C,toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m =  shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eChache = mat(zeros((self.m,2))) #误差缓存
#作为一个数据结构来使用对象，在将值传给函数时，可以通过将所有数据移到一个结构中来实现
#该方法可以实现其成员变量的填充，除了增加一个m*2的矩阵成员变量eCache外，和简化SMO一样
#eCache的第一列给出的是eCache是否有效的标志位，第二列是实际的E值

def calcEk(oS,k):
    fXk = float(multiply(oS.alpha,oS.labelMat).T* \
                (oS.X*oS.X[k,:].T))+oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek
#能够计算E的值并返回

def selectJ(i,oS,Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1,Ei]
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    #构建一个非0表,该语句返回的是非零E值所对应的alpha的值
    #nonzero()函数返回一个列表，这个列表包含以输入列表为目录的列表值
    if(len(validEcacheList))>1:
        for k in validEcacheList:
            if k==i:
                continue
            Ek = calcEk(oS,k)
            deltaE = abs(Ei-Ek)
            if(deltaE>maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
            return maxK,Ej
        #在所有的值上进行循环并选择其中使得改变量最大的那个值
    else:
        j = selectJrand(i,oS.m)
        Ej = calcEk(oS,j)
    return j,Ej

#用于选择第二个，或者说内循环的alpha的值

def updateEk(oS,k):
    Ek = calcEk(oS,k)
    oS.eCache[k] = [1,Ek]
#计算误差值并存入缓存当中，在对alpha值进行优化后会用到这个值。

接下来是用于寻找决策边界的优化例程

def innerL(i,oS):
    Ei = calcEk(oS,i)
    if((oS.labelMat[i]*Ei<-oS.tol) and (oS.alphas[i]oS.tol) and (oS.alphas[i]>0)):
        j,Ej = selectJ(i,oS,Ei)
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if(oS.labelMat[i]!=oS.labelMat[j]):
            L = max(0,oS.alphas[j] - oS.alphas[i])
            H = min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])
        else:
            L = max(0,oS.alphas[j]+oS.alphas[i]-oS.C)
            H = min(oS.C,oS.alphas[j]+oS.alphas[i])
        if L==H:
            print("L==H")
            return 0
        eta = 2,0*oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T-\
            oS.X[j,:]*oS.X[j,:].T
        if eta >= 0:
            print("eta>=0")
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei-Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS,j)
        if(abs(oS.alphas[j]-alphaJold)<0.00001):
            print("j not moving enough")
            return 0
        oS.alphas[i]+=oS.labelMat[j] *(oS.labelMat[i]*(alphaJold-oS.alphas[j]))
        updateEk(oS,i)
        b1 = oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*\
            oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]* \
             (oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b-Ej-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*\
            oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]* \
             (oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        if(0oS.alphas[i]):
            oS.b = b1
        elif (0oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1+b2)/2.0
        return 1
    else:
        return 0
    #该函数和smoSimple()几乎一样，但是这个函数使用了自己的数据结构，该结构在参数oS中传递
    # 使用selectJ()而不是selectJorand()来选择第二个alpha的值
    # 在alpha的值改变的时候才更新Ecache

完整版Platt SMO的外循环代码

def smoP(dataMathIn,classLabels,C,toler,maxIter,kTup=('lin',0)):
    oS = optStruct(mat(dataMathIn),mat(classLabels).transpose(),C,toler)
    # 构建一个数据结构来容纳所有的数据
    iter = 0
    enireSet = True
    alphaPairsChanged = 0
    while(iter0) or (enireSet)):
        alphaPairsChanged = 0
        if enireSet:
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet,iter: %d i:%d,pairs changed %d " % \
                      (iter,i,alphaPairsChanged))
            iter += 1
            # 在数据集上遍历任意可能的alpha
            # 通过调用innerL()来选择第二个alpha，并在可能是对其进行优化处理
            # 如果有任意一堆alpha的值发生变化，那么会返回1
        else:
            nonBoundIs = nonzero((oS.alphas.A>0)*(oS.alphas.A

然后对函数进行执行，观察执行效果

dataArr, lableArr = loadDataSet('F:\python\machinelearninginaction\Ch02\\testSet.txt')
b,alphas = smoP(dataArr,lableArr,0.6,0.001,40)

出现报错：optStruct() takes no arguments

原因是在定义optStruct()时将init写成了int

改正后出现新的报错：'optStruct' object has no attribute 'alpha'

语义上是optStruct 中没有alpha属性，将calcEk（）中的oS.alpha改为oS.alphas后再次执行代码，原报错解决，再次出现新的报错： 'optStruct' object has no attribute 'eCache'

按照上个报错的经验检查代码解决问题，然后再次出现报错：TypeError: '>=' not supported between instances of 'tuple' and 'int'

原因是‘>=’不支持两个不同类型字符之间的比较，将eta强制转换成int类型解决问题，再次出现报错：TypeError: only integer scalar arrays can be converted to a scalar index

经过检查发现实在定义eta时出现了将2.0打成2,0的低级错误...（已经改正）

整段代码运行成功

 运行时间得到大幅度提升，常数C一方面要保障所有样例的间隔不小于1.0，另一方面又要使得分类间隔要尽可能的大，并且要在这两方面之间尽量平衡。

刚才使用了大量时间来计算alpha的值，接下来通过alpha的值得到超平面，使用下面的函数来完成这一目的。

def calWs(alphas,dataArr,classLabels):
    X = mat(dataArr)
    labelMat = mat(classLabels).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w
    # 最终起作用的只有支持向量，其他数据点容易被舍弃

---

在复杂数据上应用核函数

径向基函数（radial basis function）

机器学习 径向基(Radial basis function)与RBF核函数 浅析_稚枭天卓-CSDN博客_rbf核函数公式

在这个例子中，将数据从一个特征空间转换到另一个特征空间，将这一过程称之为从一个特征空间到另一个特征空间的映射。通常情况下，会将低维特征空间映射到高维特征空间。

SVM优化中，所有的运算都可以写成内积。将内积替换成核函数的方式被称作核技巧。

将optStruct类以及innerL()和calEk()进行简单修改

calcEk()
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k]+oS.b)


innerL()
eta = 2.0*oS.K[i,j] - oS.K[i,i] - oS.K[j,j]
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * \
             oS.K[i,i] -oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * \
             oS.K[i,j] -oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]

class optStruct:
    def __init__(self,dataMatIn,classLabels,C,toler,kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m =  shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #误差缓存
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X,self.X[i,:],kTup)
            # kTup是一个包含核函数信息的元组
            # 在初始化方法结束后，k矩阵先被构建，然后再通过调用函数kernelTrans()进行填充
            # 全局的K值只需计算一次

在测试中使用核函数

def testRbf(k1=1.3): # 只有一个输入参数，是一个用户自定义变量
    dataArr,lableArr = loadDataSet('F:\python\machinelearninginaction\Ch06\\testSetRBF.txt')
    b,alphas = smoP(dataArr,lableArr,200,0.0001,10000,('rbf',k1))
    datMat = mat(dataArr)
    labelMat = mat(lableArr).transpose()
    svInd = nonzero(alphas.A>0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd]
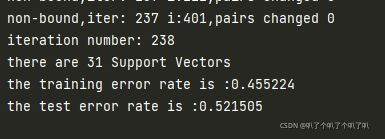
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf',k1))
        # 利用kernelTrans()函数得到转换后的数据
        predict = kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        # 再用其与前面的alpha以及类别标签值求积
        if sign(predict)!=sign(lableArr[i]):
            errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    # 如何利用核函数进行分类
    dataArr,lableArr = loadDataSet('F:\python\machinelearninginaction\Ch06\\testSetRBF2.txt')
    errorCount = 0
    datMat = mat(dataArr)
    labelMat = mat(lableArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf',k1))
        predict = kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict) != sign(lableArr[i]):
            errorCount += 1
    print("the test error rate is :%f" % (float(errorCount)/m))
    # 仅有数据集不同

随着k1的不同，测试错误率，训练错误率，支持向量个数都会变化。随着k1的变大，支持向量个数变少，错误率下降

---

基于SVM的数字识别

1.收集数据

2.准备数据

3.分析数据

4.训练算法：采用两种不同的核函数，并对径向基核函数采用不同的设置来运行SMO算法

5.测试算法：编写一个函数来测试不同的核函数并计算错误率

6.使用算法：会用到一些图像处理的知识

 增加以下函数：

def img2Vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr)
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9:
            hwLabels.append(-1)
        else:
            hwLabels.append(1)
        trainingMat[i,:] = img2Vector('%s/%s' % (dirName,fileNameStr))
    return trainingMat,hwLabels

def testDigits(kTup=('rbf',10)):
    dataArr,labelArr = loadImages('F:\python\machinelearninginaction\Ch06\digits\\trainingDigits')
    b,alphas = smoP(dataArr,labelArr,200,0.0001,10000,kTup)
    datMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    svInd = nonzero(alphas.A>0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd]
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict = kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]):
            errorCount += 1
    print("the training error rate is :%f" % (float(errorCount)/m))
    dataArr,labelArr = loadImages('F:\python\machinelearninginaction\Ch06\digits\\testDigits')
    errorCount = 0
    datMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict = kernelEval.T*multiply(labelSV,alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]):
            errorCount += 1
    print("the test error rate is :%f" % (float(errorCount)/m))

然后进行测试

 通过不同参数的设置，可以得出当参数大约取10左右时，就可以得到最小的测试错误率

也就是说最小的错误率并不对应最小的支持向量数目，可以以牺牲线性核函数的错误率来换取分类速度的提高。