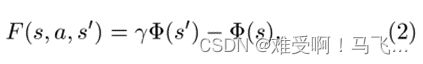Policy invariance under reward transformations- Theory and application to reward shaping基于势能的塑形奖励函数

这个是

摘要哦

本文研究了对马尔可夫决策过程的奖励函数进行修改以保持最优策略的条件。结果表明，除了效用理论（$utility$ $theory$）中常见的正线性变换外，还可以为状态之间的转换添加奖励，该奖励可以表示为应用于这些状态的任意势能函数的值的差。此外，这被证明是不变性的必要条件，因为任何其他转换都可能产生次优策略，除非对基础MDP做出进一步假设。这些结果揭示了奖励塑形的实践，这是一种用于强化学习的方法，通过额外的训练奖励来指导学习器。特别是，奖励塑形过程中的一些众所周知的“错误”被证明是由非基于势能的奖励产生的，并给出了与基于距离和基于子目标的启发式方法相对应的塑形势能的方法。我们表明，这种势能可以导致学习时间的大幅减少。

1. Introduction

----在动态规划和强化学习文献中研究的顺序决策问题中，“任务”由奖励函数表示。给定奖励函数和域模型(a model of the domain)，确定最优策略。出现的一个基本理论问题是：我们在指定奖励函数时有什么自由度，以使最优策略保持不变？

----在主要研究单步决策的效用理论领域，效用函数的相应问题可以非常简单地回答。对于没有不确定性的单步决策，效用上的任何单调变换都会使最优决策在不确定性下保持不变，只允许正线性变换[von Neumann和Morgenstern 1944]。这些结果对于设计游戏中的评估函数、从人类那里获得效用函数以及许多其他领域具有重要意义。

----据我们所知，对于顺序决策问题，尚未充分探讨奖励函数变换下的策略不变性问题。至少在以下方面，策略保持变换很重要：
MDPs的结构估计任务[Rust，1994]涉及从观察到的最优行为中恢复模型和奖励函数。（另见[Russel，1998]中对反向强化学习的讨论。）策略保持转换决定了奖励函数可以恢复的程度。

----强化学习中奖励塑形的实践包括向学习代理提供额外的奖励，以指导其学习过程超出底层 MDP 提供的奖励。 重要的是要了解塑形对学习策略的影响。

----本文主要关注奖励塑形，它有可能成为一种非常强大的技术(PS：Ng大神真的是高瞻远瞩，现在看来，基于势能的塑形奖励确实是一个强大的技术，这可是1999年提出的思想呀)，用于扩展强化学习方法以处理复杂问题[Dorigo和Colombetti 1994 Mataric，1994，Randløv和Alstrøm，1998]。（在动物训练文献中也出现了类似的想法，参见[Saksida等人1997年的讨论]。）通常情况下，一个非常简单的额外奖励模式足以直接解决一个完全棘手的问题。

----要了解为什么策略不变性在塑形中很重要，请考虑以下可能出现的错误示例：[Randløv 和 Alstrom，1998 年] 描述了一个学习骑模拟自行车到特定位置的系统。为了加快学习速度，每当agent朝着目标取得进展时，他们都会提供积极的奖励。agent学会了在起跑状态附近的小圈子里骑车，因为骑车离开球门不会受到处罚。大卫·安德烈（David Andre）和阿斯特罗·特勒（Astro Teller）训练的足球机器人也出现了类似的问题。因为足球比赛中控球很重要，所以他们提供了触球保护。agent学会了一种策略，即它保持在球旁边并“振动”，尽可能频繁地接触球。这些策略显然不适合最初的MDP。

----这些例子表明，如果不误导agent学习次优策略，塑形奖励必须遵守某些条件。正奖励周期的困难导致人们考虑从保守势能中获得的奖励，即在两个状态之间执行转换的奖励是应用于每个状态的势能函数的值的差。事实证明，这不仅是在奖励转换下保证策略不变性的充分条件，而且，假设没有MDP的先验知识，这也是能够做出这种保证的必要条件。第2节给出了准确陈述该权利要求所需的定义，第3节陈述并证明了该权利要求。第4节展示了如何构建各种类型的塑形势能，并展示了它们在一些简单领域加速学习的效果。最后，第5节将我们的结果与现有算法联系起来，如优势学习[Beird，1994]和A-policy迭代[Bertsekas和Tsitsiklis1996]，并以讨论和未来工作结束。

2. Preliminaries

2.1 Definitions

------在本节中，我们提供了本文中使用的一些定义，重点是有限状态马尔可夫决策过程（MDPs）的情况。在有限状态和无限状态问题中，塑形对我们来说都很重要，但即使在没有塑形的情况下，无限状态情况下的MDP理论也要困难得多。然而，一旦基本的MDP理论被提出，我们的分析和方法很容易从有限状态空间推广到无限状态空间，稍后我们将再次提及这一点；但现在，让我们从只考虑有限状态域开始定义。

------有限状态马尔可夫决策过程（MDP）是一个元组$M=(S,A,T,\gamma ,R)$，其中：S是有限状态集；$A=a_1，..，a_k$是一组k>2的动作集；$T=P_{sa}(\cdot )|s\in S,a\in A$是下一状态转移概率，其中$P_{sa}(s^{\prime })$给出了在状态$s$中采取动作$a$时转移到状态$s^{\prime }$的概率；$\gamma =(0,1)$是折扣系数；$R$指定奖励分配。为了简单起见，我们将假设奖励是确定性的，在这种情况下，$R$是一个称为奖励函数的有界实函数。在文献中，奖励函数通常写为$R:S\times A\to \mathbb{R}$（暂时可以把这个空心的$\mathbb{R}$看做是实数），其中$R(s,a)$是在状态$s$中采取行动$a$时获得的奖励。虽然我们经常以这种形式编写奖励函数，但我们也允许使用更一般的形式$R:S\times A\times S\to \mathbb{R}$，其中$R(s,a,s^{\prime })$是在状态$s$中采取行动$a$并过渡到状态$s^{\prime }$时收到的奖励。

----给定一组固定的动作$A$，一组状态$S$上的策略是任何函数$\pi ：S\to A$, 请注意，策略是在状态上定义的，而不是在MDP上定义的。因此，只要两个MDP使用相同的状态和动作，相同的策略就可以应用于两个不同的MDP。给定状态S上的任何策略$\pi$和使用相同状态和动作的任何MDP $M=(S,A,T,\gamma ,R)$，然后我们可以定义值函数$V_M^{\pi }$，该函数在任何状态$s$下求值，得到$V_M^{\pi }(s)=E[r^1+\gamma r^2+\gamma ²r^3+\dots ..；\pi ,s]$，其中$r_i$是从状态$s$执行策略$\pi$的第$i$步收到的奖励，期望值是执行$\pi$时所发生的状态转换。然后，我们将最优值函数定义为$V_M^{\ast }(s)=su{p}_{\pi }{V}_M^{\pi }(s)$，$Q$函数在任意$s\in S$，$a\in A$下求值为

------(其中符号$s^{\prime }$~$P_{sa}(\cdot )$表示$s^{\prime }$是根据分布$P_{sa}(.)$绘制的），最佳$Q$函数为$Q_M^{\ast }(s)=su{p}_{\pi }{Q}_M^{\pi }(s,a)$ 。最后，我们将MDP $M$的最优策略定义为${\pi }_M^{\ast }(s)=argma{x}_{a\in A}{Q}_M^{\ast }(s,a)$。最优策略可能不是唯一的，我们更一般地说, 如果对所有 $s\in S$ ,都有 $\pi (s)\in argma{x}_{a\in A}{Q}_M^{\ast }(s,a)$，则策略 $\pi$ 在 $M$ 中是最优的。 最后，当上下文 MDP 明确时，我们也可以删除 $M$ 下标，并写成 $V^{\pi }$ 而不是$V_M^{\pi }$等。

我们还需要一些（基本上是标准的）规则性条件，以确保上述所有定义都有意义。对于未贴现(γ=1)MDP，我们假设s包含一个称为吸收状态$s_0$的特殊状态$s_0$，MDP在转移到$s_0$后“停止”，此后没有进一步的奖励。此外，对于未贴现的MDP，我们再次假设所有策略都是正确的，这意味着在从任何状态开始执行任何策略时，我们将以概率1最终转移到$s_0$。由于这确实是T上的一个条件，因此我们将在本文中说，如果该条件成立，则过渡概率T是正确的。贴现的MDPs没有相应的吸收状态，总是无限的视界；因此，请注意，对于它们，我们可以写S-{$s_0$}＝S。

----以上是具有有限状态空间的MDP所需的标准规则性条件（参见[Sutton和Barto，1998]），这是我们明确表示将重点关注的情况。对于具有无限状态空间的 MDP，将需要更多：例如，在未折扣的情况下，我们定义的 $V_M^{\pi }(s)=E[r1+yr2+y²r3+.\dots .;\pi ,s]$ 中的期望甚至可能不存在。在我们甚至可以定义诸如最优政策之类的东西之前，这些问题需要得到妥善解决，这些材料的优秀来源包括 [Bertsekas 1995，Hernández-Lerma，1989，Bertsekas 和 Shreve 1978]。但不幸的是，完全一般性地解释无限|S|情况将需要比我们希望在这里深入研究的更多的度量理论，并且我们只评论，通过对MDP上所需正则性条件的适当推广，我们的所有结果都很容易推广到无限|S|情况。在本文中，我们将不断地联系如何证明无限|S|的结果，尽管我们将无限|S|的更一般证明推迟到全文。现在我们只注意到对于无限状态的情况，一个重要且有用的条件是增强的绝对值是有界的； 这将在本文后面再次提及。

2.2 Shaping Rewards

----在本节中，我们将介绍塑形奖励的正式框架。直觉上，我们正在尝试学习一些MDP $M=(S,A,T,\gamma ,R)$的策略，我们希望通过给予它额外的“塑形”奖励来帮助我们的学习算法，这将完全引导它更快地学习好(或最佳)策略。为了形式化这一点，我们假设，不是在$M=(S,A,T,\gamma ,R)$上运行强化学习算法，而是在一些修改的MDP $M^{\prime }=(S,A,T,\gamma ,R^{\prime })$上运行，其中$R^{\prime }=R+F$是修改的MDP中的奖励函数，$F：S\times A\times S\to \mathbb{R}$是一个有界实值函数，称为塑形奖励函数。（类似于$R$，对于未折扣的情况，$F$的域应该严格为S-{$s_0$}×A×S，但我们现在不会对这一点过于迂腐。）因此，如果在原始MDP $M$中，我们会收到从动作$a$的$s$转换到$s^{\prime }$的奖励$R(s,a,s^{\prime })$，那么在新的MDP $M^{\prime }$中，我们将收到相同事件的奖励R。

----对于任何固定的MDP，假设无记忆的加性塑形奖励函数，这个$R^{\prime }=R+F$是塑形奖励的最一般的可能形式。更重要的是，它们涵盖了人们可能会想到的相当大范围的塑形奖励。例如，为了鼓励agent朝着一个目标前进，人们可以选择$F(s,a,s^{\prime })=r$，只要$s^{\prime }$比$s$更接近目标（在任何适当的意义上），否则$F(s,a,s^{\prime })=0$，其中$r$是一些积极的奖励。或者，为了鼓励在一些状态集合$s_0$中采取动作$a_1$，可以在$a＝a_1$，$s\in s_0$时设置$F(s,a,s^{\prime })＝r$，否则$F(s,a,s^{\prime })=0$。

—这种形式的奖励转换的一个基本但重要的特性是，它通常可以实现：在许多强化学习应用程序中，我们没有明确地将$M$作为元组$<S,A,T,\gamma ,R>$的形式给出，而只允许通过在MDP中采取动作并观察所产生的状态转换和奖励来了解$M$。给定对$M$的这种访问，我们可以简单地通过在$M$中采取动作来模拟对M’的相同类型的访问，然后“假装”每当我们在$M$中实际观察到回报$R(s,a,s^{\prime })$时，我们就观察到了奖励$R(s,a,s^{\prime })+F(s,a,s^{\prime })$。自然，这起作用的简单原因是$M$和$M^{\prime }$使用相同的动作、状态和转换概率。因此，可以应用于$M$的在线/离线基于模型的/无模型的算法通常可以以相同的方式容易地应用于$M^{\prime }$。

----由于我们正在学习$M^{\prime }$的策略，希望在$M$中使用它，因此当前的问题如下：对于什么形式的奖励函数F，我们可以保证$M^{\prime }$中的最优策略${\pi }_{M^{\prime }}^{\ast }$在$M$中也是最优的？下一节将大致回答这个问题。

3. Main results

—在实际应用中，我们通常并不完全先验地知道 $T$（并且可能知道也可能不知道 $R(s,a,s^{\prime })$）。因此，我们的目标是，在给定 $S$ 和 $A$（可能还有 $R$）的情况下，得出一个“好”的塑形奖励函数 $F：S\times A\times S\to \mathbb{R}$，这样 ${\pi }_{M^{\prime }}^{\ast }$在 $M$ 中将是最优的。在本节中，我们将给出 F 的一种形式，在这种形式下我们可以保证 ${\pi }_{M^{\prime }}^{\ast }$在 $M$ 中是最优的。我们还提供了一个弱逆，表明在没有进一步了解 $T$ 和 $R$ 的情况下，这是始终可以提供这种保证的唯一类型的整形函数。

—首先关注未折扣的情况 ($\gamma =1$)，让我们尝试获得一些直觉，了解什么样的 $F$ 可能会导致引言中指出的塑形“错误”。在Randløv和Altrøm的自行车任务中，当agent因骑向球门而获得奖励，但因骑离球门而没有受到惩罚时，它学会了在一个小圆圈中骑行，从而在它碰巧朝球门移动时获得积极的奖励。更一般地说，如果存在某种状态序列$s_1,s_2,\dots ,s_n$，使得代理可以在一个周期（$s_1\to s_2\to \dots \to s_n\to s_1\to \dots$）中穿过这些状态序列，并通过这种行为获得净的积极（正数，正的）塑形奖励$(F(s_1，a_1，s_2)+\dots +F(s_{n-1}，a_{n-1}，s_n)+F(s_n，a_n，s_1)>0)$，那么代理似乎可能会“分心”于它真正应该做的事情（例如朝着目标骑行），而是尝试重复执行这个周期。

—为了解决循环的这一困难，$F$的一种形式是让$F$是势能的差：$F(s,a,s^{\prime })=\Phi (s^{\prime })-\Phi (s)$，其中$Ф$是状态上的函数。这样，$F(s_1,a_1,s_2)+\dots +F(s_{n-1}，a_{n-1}，s_n)+F(s_n，a_n，s_1)=0$，我们消除了“分心”agent的循环问题。还有其他选择$F$的方法吗？除了周期之外，我们还需要解决塑形方面的其他问题吗？事实证明，在没有更多关于$T$和$R$的先验知识的情况下，这种基于势能的塑形函数$F$是唯一能够保证与M中的最优策略一致的$F$。此外，事实证明，这基本上是我们做出这种保证所需的全部。在以下定理中，这是正式的：

-----定理 1. 给定任意 $S,A,\gamma$和任意塑形奖励函数$F:S\times A\times S\to \mathbb{R}$。如果存在实值函数 $Ф:S\to R$ 使得对于所有 $s\in S$-{$s_0$}, $a\in A$, $s^{\prime }\in S$，我们称 $F$ 是基于势能的塑形函数，

----(其中 S-{$s_0$} =S if $\gamma <1$）。那么，$F$ 是一个基于势能的塑形函数是它保证与最优策略（当从 $M^{\prime }=(S,A,T,\gamma ,R+F)$ 而不是来自 $M=(S,A,T,\gamma ,R)$)，在以下意义上：

（充分性）如果 $F$ 是基于势能的塑形函数，则 $M^{\prime }$ 中的每个最优策略也将是 $M$ 中的最优策略（反之亦然）。

（必要性）如果$F$不是基于势的塑形函数（例如，不存在满足方程（2）的函数），则存在（适当的）转换函数$T$和奖励函数$R:S\times A\to \mathbb{R}$, 使得$M^{\prime }$中没有最优策略在$M$中是最优的。

----还请注意：对于无限状态情况，如果要选择一些$Ф$来构造基于势能的塑形函数，那么对于要通过的形式结果，我们确实应该要求$Ф$是有界的，这样塑形奖励$F$也是有界的（类似于$R$是有界条件）。在第2.1节中，稍后将再次讨论此问题。注意，对于有限状态情况，这是一个真空条件，因为$Ф$在有限基数范围内会自动有界。此外，上述必要性和充分性条件似乎比通常情况更复杂，这是因为在$M$或$M^{\prime }$中可能存在多个最优策略。然而，应该清楚的是，所使用的量化使得这是这种形式的最强定理。充分条件表明，只要我们使用基于势能的 $F$，就可以保证我们可能尝试学习的任何 ${\pi }_M^{\ast }$ 在 $M$ 中也是最优的。必要条件说，如果我们不知道 $T$ 和 $R$，那么如果我们想保证与学习 $M$ 中的最优策略的一致性，我们必须选择一个基于势能的 $F$ 来学习 $M^{\prime }$。（如果我们确实对 $T、R$ 有深入的了解，那么必要条件就不多说了，我们可能可以使用其他塑形函数。）

----附录A中给出了必要性证明。这里，我们仅证明方程（2）是一个充分条件：如果$F$确实是（2）中的形式，那么我们可以保证$M^{\prime }$中的每个最优策略在$M$中也是最优的。再次，我们仅在有限$|S|$；无限$|S|$的证明几乎相同，但在证明使用Bellman方程的合理性时需要稍微谨慎一些。

证明（充分性）：设 $F$ 为 (2) 中给出的形式。如果 $\gamma =1$，那么对于任何常数$k$，用 ${\Phi }^{\prime }(s)=\Phi (s)-k$ 替换$\Phi (s)$不会改变塑形奖励 $F$（这是这些势能的差），如有必要，我们可以通过用 $\Phi (s)-\Phi (s_0)$ 替换 $\Phi (s)$，不失一般性地假设用于通过 (2) 表达 $F$ 的 $\Phi$ 满足 $\Phi (s_0)=0$。

对于原始的 MDP $M$，我们知道其最优 $Q$ 函数 $Q_M^{\ast }$ 满足贝尔曼方程（参见 [Sutton and Barto,1998]）

------但这正是 $M^{\prime }$ 的贝尔曼方程。 对于未折扣的情况，我们还有 ${\hat{Q}}_{M^{\prime }}(s_0,a)=Q_M^{\ast }(s_0,a)-Ф(s_0)=0-0=0$。 因此， 满足 $M^{\prime }$ 的 Bellman 方程，并且实际上必须是唯一的最优 $Q$ 函数。 因此，${\hat{Q}}_{M^{\prime }}(s_0,a)=Q_M^{\ast }(s,a)-\Phi (s)$ ，因此$M^{\prime }$的最优策略满足

因此在 -----$M$ 中也是最优的。证明 $M$ 中的每个最优策略在 $M^{\prime }$ 中也是最优的。 简单地应用相同的证明，但 $M$ 和 $M^{\prime }$ 的角色互换（并使用塑形函数-$F$）。 这就完成了证明。

推论 2. 在定理 1 的条件下，假设 $F$ 确实采用 $F(s,a,s^{\prime })=Ф(s^{\prime })-Ф(s)$ 的形式。进一步假设如果 $\gamma =1$，则 $Ф(s_0)=0$。 那么对于所有的 $s\in S,a\in A$,

证明： (3) 在上面的充分性证明中被证明 (4) 紧随恒等式 $V\ast (s)=ma{x}_{a\in A}{Q}^{\ast }(s,a)$ 。

备注1（鲁棒性和学习）：虽然我们没有在这里证明，但推论2中的恒等式实际上适用于任意策略$\pi$，而不仅仅适用于最优策略：$V_{M^{\prime }}^{\pi }(s)=V_M^{\pi }(s)-\Phi (s)$ （$Q$函数也是如此）。这样做的结果是，基于势能的塑形是鲁棒的，因为几乎最优的策略也得到了保留；也就是说，如果我们使用基于势能的塑形来学习$M^{\prime }$(例如，$|V_{M^{\prime }}^{\pi }(s)-V_M^{\pi }(s)|<\epsilon$ 中的近似最优策略$\pi$，那么在$M$中也将是近似最优的。（为了证明这一点，我们将刚才指出的恒等式应用于策略$\pi$和${\pi }_M^{\ast }={\pi }_{M^{\prime }}^{\ast }$，然后进行减法。）

备注2（$Ф$下的所有策略都是最优的）：为了更好地理解为什么基于势能的$F$保持最优策略，值得注意的是，如果我们有一个MDP $M$，它具有基于势能的强化函数$R(s,a,s^{\prime })=\gamma Ф(s^{\prime })-Ф(s)$，那么任何策略在$M$中都是最优。因此，基于势能的塑形函数对策略无动于衷，因为它们没有理由让我们偏爱任何其他策略。；在直觉层面上，这解释了为什么当我们从$M$切换到$M^{\prime }$时，他们没有给我们任何理由选择${\pi }_M^{\ast }$以外的任何策略。

------该定理建议我们选择$F(s,a,s\prime )=\gamma Ф(s\prime )-Ф(s)$形式的塑形奖励。在应用中，$\Phi$当然应该使用有关领域的专家知识来选择。至于如何做，推论2 提出了$\Phi$的一个特别好的形式，如果我们对域足够了解，可以尝试选择它。我们看到，如果$\Phi (s)=V_M^{\ast }$ (在未折扣的情况下$\Phi (s_0)=0$），那么方程（4）告诉我们$M^{\prime }$中的值函数是$V_{M^{\prime }}^{\ast }\equiv 0$----这是一个特别容易学习的值（状态值）函数；即使缺乏一个世界模型，所有要做的就是学习非零$Q$值。虽然为了避免误解，我们也强调这不是选择有用$\Phi$的唯一方法，即使$Ф$与$V_M^{\ast }$相距甚远（比如在超规范中，例如通过引导探索等），这种塑形奖励也会有很大的帮助，我们将在下一节中看到这方面的例子。但是，在任何情况下，只要我们选择基于势能的$F$，我们就可以保证我们在$M^{\prime }$中学习到的任何（接近）最优策略在$M^{\prime }$也会是（接近）最佳的。现在，让我们将注意力转向一些小实验，这些小实验演示了基于势能的塑形如何在实践中应用。

4. 实验

----我们面前的许多实证工作令人信服地证明了塑形的使用 [Mataric, 1994, Randløv 和 Alstrøm, 1998]，我们不会费心去进一步证明它的使用。在这里，我们的目标是展示势能风格的塑形函数如何融入图片，并展示如何在实践中推导出此类塑形函数。

----为了实现这些目标，为了简单明了，我们选择使用非常简单的网格世界域来展示基于势能的塑形的有趣方面。第一个域是一个到目标的最短路径 10x10 网格世界，开始和目标状态位于对角，没有折扣，每步强化一次。 动作是 4 个罗盘方向，80% 的时间向预期方向移动 1 步，20% 的时间向随机方向移动 1 步，如果agent试图离开网格，它会停留在同一个地方。什么是一个好的塑形势能$Ф(s)$？ 我们之前已经指出，方程 (4) 表明 $Ф(s)=V_M^{\ast }(s)$ 可能是一个很好的塑形势能。那么现在让我们来看看可能暗示 $V_M^{\ast }$ 粗略估计的推理类型；通过这样做，我们希望证明，在对距离和目标位置有一点专业知识的情况下，类似的推理可能可以用于类似地推导出其他最小成本目标问题。

—在尝试朝着目标迈出一步时，我们有 80% 的机会朝着目标迈出期望的一步，并且有 20% 的机会采取随机行动。 如果我们采取随机行动，那么除非我们处于网格世界的边界，否则我们朝着目标移动的可能性与远离目标的可能性一样大。因此，从大多数状态来看，我们期望最优策略在每个时间步向目标迈出大约 0.8 步（曼哈顿距离，MANHATTAN），粗略估计从 $s$ 到达目标所需的预期步数为${}_{MANHATTAN}(s,GOAL)/0.8$ . 因此，我们将价值函数的估计值和 $Ф(s)$ 设为${Ф}_0(s)={\hat{V}}_M(s,a)={-}_{MANHATTAN}(s,GOAL)/0.8$。 这就是我们对“良好”塑形函数的猜测。 此外，作为与 $V_M^{\ast }(s)$ 相去甚远（在支持范数中）的塑形奖励，我们还尝试使用 $Ф(s)=0.5{Ф}_0(s)$。 第一个实验的结果如图 1(a) 所示。 (本节中报告的所有实验都是 40 次独立运行的平均值。)可以很容易地看出，使用这些塑形函数中的任何一个都可以显着帮助加快学习速度。 此外，值得再次强调的是，即使 $0.5{Ф}_0(s)$ 与 $V_M^{\ast }$ 相去甚远，它仍然对学习的初始阶段有显着帮助。 对于更大的 50x50 网格世界，结果变得更加引人注目：图 1b 显示了在更大的网格上重复相同实验的结果。 ${Ф}_0(s)$ 和 $0.5{Ф}_0(s)$ 的图在图中非常低，几乎看不见； 没有塑形的学习显然无可救药地输给了基于势能的塑形算法。

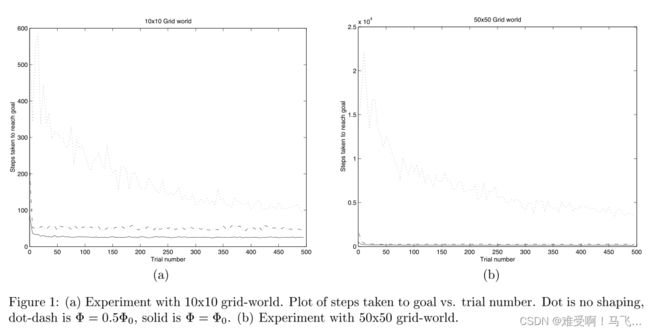
----重申一下，这些实验的目的不是试图证明塑形的合理性——其他人已经做得更有说服力了。相反，我们在这里展示的是一种非常简单的推理风格，通过将距离目标启发式组合在一起，我们能够选择一个合理的 $Ф$，从而显着加快学习速度。

----接下来，类似推理风格可能适用的另一类问题是我们可以分配子目标的领域。考虑图 $2a$ 中的网格世界，我们从左下角开始，在进入最终目标状态之前必须按顺序拾取一组“flags”。 动作和奖励与之前的网格世界相同，并且状态空间被扩展以跟踪收集到的标志。 由于每个标志都是一个子目标，因此很容易选择 $F$，以便我们因访问子目标而获得奖励。 现在让我们看看势能函数推理风格如何确实可以引导我们选择这样的 $F$，以及等式（4）如何进一步暗示子目标奖励的大小。

----了解子目标位置并使用类似于之前建议的推理（每个时间步长 0.8 步等），我们可以估计达到目标所需的预期时间步数，例如 $t$。如果我们想象每个子目标与前一个子目标的实现难度差不多，那么在达到第 $n$ 个子目标后，我们仍然有大约 $((5-n)/5)t$ 步要走。一个稍微更精细的论点将其更改为$((5-n-0.5)/5t$步数（其中0.5来自“典型情况”，即我们位于第$n$个子目标和第$n+1$个子目标之间的中间位置，因此我们的首选$Ф(s)$是${Ф}_0(s)=((5-ns-0.5)/5)t$，其中$ns$表示我们在s时实现的子目标数。使用这种形式的塑形奖励函数，我们可以看到，当我们达到任何子目标（除了最终目标状态）时，$Ф(s)={Ф}_0(s)$跳跃$t/5$，因此塑形奖励函数$F(s,a,s^{\prime })=Ф(s^{\prime })-Ф(s)$为达到每个子目标提供$t/5$奖励。这正是我们的直觉所暗示的，可能是一个很好的塑形奖励。为了进行比较，我们还使用了一个更精细的塑形奖励进行了这项实验，与之前的网格世界实验类似，该奖励明确地估计了每个状态的剩余目标时间，并构建了相应的${Ф}_1(s)={\hat{V}}_M(s)$势能函数。这些实验的结果如图 $2b$ 所示，我们看到使用我们的第一个粗略塑形函数 ${Ф}_0$ 比不使用塑形函数可以显着加快学习速度（微调 ${Ф}_1$ 不出所料地提供了更好的性能）。当在更大的领域或更多的子目标上重复这个实验时，结果（此处未报告）变得更加引人注目。

5. 讨论

----我们已经证明了塑形函数$F$保持最优策略不变的充分必要条件。这里有两个值得一提的简单概括：除了在尝试学习最优策略时保证一致性之外，很容易证明（通过类似于第3节中备注1的论证），当试图从受限的策略类别中学习好策略时，基于势能的F也有效，例如在[Kearns等人1999年]中研究的框架中（例如，该框架包括为从状态到动作的神经网络映射找到最佳权重的任务）。此外，对于半马尔可夫决策过程（SMDP），其中动作需要不同的时间来完成方程（2），毫不奇怪地推广到$F(s,a,s^{\prime },\tau )=e^{-\beta \tau }\Phi (s^{\prime })-\Phi (s)$，其中t是动作完成所需的时间，$\beta$是折现率。

----最后，$\gamma Ф(s’)-Ф(s)$形式在表面上似乎也让人联想到优势学习[Bird1994]和$\lambda$-策略迭代[Bertsekas和Tsitsiklis1996]中使用的一些方程中的术语。在一个非常粗糙的层面上，事实证明，它们中的每一个都可能被认为是试图修改$Ф$，以获得一些计算或表示优势。如果我们考虑修改$Ф$的问题，那么尝试学习一个粗糙的塑形函数似乎会很自然地导致一个多尺度值函数逼近的算法；尽管最初尝试学习一个塑形函数可能看起来很不寻常，但这是多尺度的“粗糙与精细”近似方面，这使得它可能很强大；这将是未来工作的主题。

----在本文中，我们证明了基于势能的塑形奖励$\gamma Ф(s^{\prime })-Ф(s)$保持（接近）最优策略不变。此外，这被证明是唯一能够保证这种方差的塑形类型，除非我们对MDP做出进一步的假设。但正如一些从业者甚至在未计算的问题上使用折扣（可能是为了提高算法的收敛性），我们相信，未来对势能风格塑形奖励的经验也可能会导致人们偶尔尝试塑形受势能启发的奖励，但这些奖励可能并不严格符合我们给出的形式。例如，类比于在未贴现问题上使用贴现，可以想象，对于某些问题，即使在$\gamma \ne 1$尽管在这种情况下，我们的定理可能不再保证最优性，但纯粹从工程的角度来看，这样的塑形函数仍然值得谨慎地尝试。本着同样的精神，尽管我们的正则性条件要求使用有界$Ф$，但也有可能一些从业者想要尝试某些无界$Ф$。当然，如果有关领域的专家知识可用，那么非势能的塑形函数也可能是完全合适的。

----作为选择塑形函数的准则，我们提出了基于距离的启发式和基于子目标的启发式来选择势能；因为塑形对于使学习变得容易理解至关重要，我们认为寻找良好塑形函数的任务将是一个越来越重要的问题。

个人总结

势能塑型奖励函数的作用是解决在添加塑型奖励函数时，agent的一种刷分情况。其实，受到环境和奖励函数的影响，agent还有很多种刷分情况，强化学习社区称之为“reward hacking”，即奖励黑客，关于“reward hacking”，可以参考这篇论文Defining and Characterizing Reward Hacking。
在某些情况下，受到环境和塑形奖励的影响，agent总能找到一个刁钻的路径来刷分。Ng将塑形奖励定义为$F(s,a,s^{\prime })=Ф(s^{\prime })-Ф(s)$这种形式，这样的话，在一个闭环路径中，这个塑形奖励得到的最终奖励还是0，这样就可以有效避免刷分了。