moravec算法
一、算法
(1)原理
该算法将角点定义为具有低“自相关性”的点。
算法会检测图像的每一个像素,将像素周边的一个邻域作为一个patch,并检测这个patch和周围其他patch的相关性。这种相关性通过两个patch间的平方差之和(SSD)来衡量,SSD值越小则相似性越高。
如果像素位于平滑图像区域内,周围的patch都会非常相似。SSD会很小。
如果像素在边缘上,则周围的patch在与边缘正交的方向上会有很大差异,在与边缘平行的方向上则较为相似。某一个方向SSD很小,其他方向存在很大差异。
如果像素是各个方向上都有变化的特征点,则周围所有的patch都不会很相似。所有方向SSD都会很大。
(2)算法实现
1、依次以每个像素点为锚点计算其5x5的窗口内4个方向的SSD,记为S1,S2,S3,S4
2、设定该点角点响应为:CFRx,y=min{S1,S2,S3,S4}
3、设定一个阈值R,则角点响应值大于R的认为是候选角点。
4、局部非最大值抑制。(防止局部窗口内出现过各角点)
(3)缺陷
1、强度值的计算并不是各向同性的,只有离散的8个45度角方向被考虑。因为patch的评议比较最多只有8个方向;
2、由于窗口是方形并且二元的,因此相应函数会有噪声
3、对边缘的相应太简单,因为强度值尽取SSD的最小值
4、噪声和角点性质一样,所以对噪声敏感,可以通过增加滑动窗口的大小来抑制噪声,但计算量会增大
(4)算法流程
首先依次算各个方向差、然后求取限定的局部最大值。该算法较为简单不在赘述。
二、代码(C++)
注:代码需要配置opencv库
(1)moravec.h头文件
#pragma once
#include
#include
#include "moravec.h"
#include "gdal_priv.h"
#include "cpl_conv.h"
#include
#include
#include
#include
#include
#include
using namespace std;
using namespace cv;
//定义moravec算法,实现特征提取
class moravec
{public:
void Moravec_1(Mat image);
};
(2)moravec.cpp文件
#define _CRT_SECURE_NO_DEPRECATE
#include "moravec.h"
void moravec::Moravec_1(Mat image)
{
if (image.empty()) //如果为空
{
std::cout << "Could not open or find the image." << std::endl;
}
int CandidateWin = 5, window = 5; //候选区窗口大小(非极大值抑制作用),移动窗口大小(滑动的小窗口)
//int candiPositionR = 0, candiPositionC = 0, i, j, g; //row行,col列,i候选区行,j候选区列
int k = int(window / 2); //窗口中心像元
double WinMax = 0;//候选区最大值
int window_min = 0;//滑动窗口最小值,目的时求取四个方向的最小值
int MaxPositionR = 0; int MaxPositionL = 0;
int CandidateWinPR = 0, CandidateWinPC = 0;//row行,col列,i候选区行,j候选区列
int windowPR = 0, windowPC = 0;
Mat Candidate = Mat(image.size(), CV_8UC1, Scalar(0));
//首先小窗口滑动
for (windowPR = k;windowPR <= image.rows-2-k; windowPR++)
{
for (windowPC = k+1; windowPC <= image.cols-2-k; windowPC++)
{
int V[4] = { 0, 0, 0, 0 };
for (int i = -k; i <= k; i++)
{
//for (int j = -k; j <= k; j++)
//{
V[0] = V[0] + pow(image.at(windowPR , windowPC+i )- image.at(windowPR , windowPC + i +1), 2);//水平方向
V[1] = V[1] + pow(image.at(windowPR + i, windowPC + i) - image.at(windowPR + i+1, windowPC + i+1), 2);//右下角
V[2] = V[2] + pow(image.at(windowPR+i , windowPC ) - image.at(windowPR+i+1, windowPC ), 2);//竖直方向
V[3] = V[3] + pow(image.at(windowPR + i, windowPC + i) - image.at(windowPR + i + 1, windowPC - i - 1), 2);//左下角
//}
//cout << "V[0]" << V[0] <<" V[1]" << V[1] <<" V[2]" << V[2] << "V[3]" << V[3] << endl;
}
//cout << "windowPR=" << windowPR << "windowPC=" << windowPC << endl;
int Vmin = V[0];
//if (V[0] < Vmin) Vmin = V[0];
if (V[1] < Vmin) Vmin = V[1];
if (V[2] < Vmin) Vmin = V[2];
if (V[3] < Vmin) Vmin = V[3];
//cout << Vmin << endl;
Candidate.at(windowPR, windowPC) = Vmin;
}
}
imshow("Moravec算子3*3",Candidate);
//小范围区域筛选最大值
for (int i = 0; i + CandidateWin <= Candidate.rows - CandidateWin - 1; i = i + CandidateWin)
{
for (int j = 0; j + CandidateWin <= Candidate.cols - CandidateWin - 1; j = j + CandidateWin)
{
int winMax = Candidate.at(i, j);
for (int m = 0; m <= CandidateWin-1; m++)
{
for (int n = 0; n <= CandidateWin-1; n++)
{
if (Candidate.at(i + m, j + n) > winMax)
{
winMax = Candidate.at(i + m, j + n);
MaxPositionR = i + m;
MaxPositionL = j + n;
}
//cout << "m=" << m << " n=" << n << endl;
}
}
if (winMax >200)
{
Point pt = Point(MaxPositionL, MaxPositionR);
circle(image, pt, 3, Scalar(255, 0, 0));
}
//cout << "m=" << i << " n=" << j << endl;
}
cout << "m=" < (3)main函数
#define _CRT_SECURE_NO_DEPRECATE
#include
using namespace std;
#include "moravec.h"
using namespace cv;
using namespace std;
int main()
{
Mat M = imread("D:\\Users\\Ou\\Desktop\\测试图片\\Lanny.png", IMREAD_GRAYSCALE);
std::cout << "图像的类型编号为:" << M.type() << endl; //网上有类型对应的编号
std::cout << "图像的通道数量为:" << M.channels() << endl;
moravec A;
A.Moravec_1(M);
waitKey();
cv::waitKey(0);//等待用户需要多长时间毫秒,零意味着永远等待
return 0;
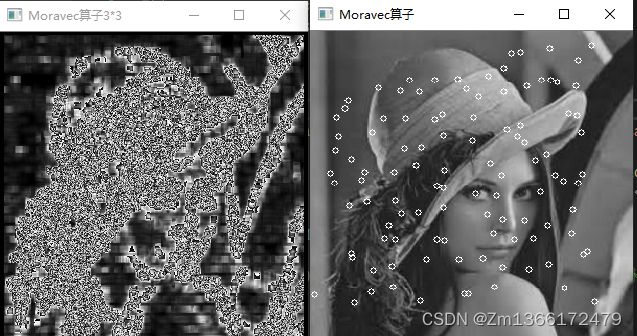
} 三、代码结果
左图为未进行极大值抑制的结果
四、算法补充
1、IOU(交并比);两个窗口交集/两个窗口并集。
2、非极大值抑制:即求取最大值的位置保留
五、算法思考
1、该算法每个块是独立的,很有可能对于第一个窗口的最大值<第二个窗口的最小值,及时窗口1在全图中不能算是特征点,但是由于算法缺陷仍然会被认为是特征点。
2、小窗的大小选择一定程度上会影响结果,通过什么办法可以实现最优窗口的选择。
3、非极大值抑制为什么不直接通过扩大滑动窗口来增加范围,以减少运算。