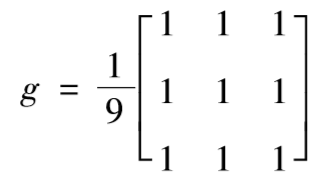从计算机视觉到人脸识别：一文看懂颜色模型、信号与噪声

导读：计算机视觉是计算机科学的一个重要门类。计算机视觉的主要目标是教会计算机如何去“看”，所以也称为机器视觉。本文将介绍计算机视觉的一些基础知识。

作者：王天庆

如需转载请联系华章科技

01 计算机视觉介绍

计算机视觉的主要目标是教会计算机如何去获取图片信息中的知识，例如人脸识别就是让计算机去自动获取与识别人脸图像中的知识，这个“知识”的范畴可以是“两张图片中的人脸是否来自于同一个人”，也可以是“图片中的人脸是男人还是女人”。

维基百科上对计算机视觉的定义如下：

Computer vision is an interdisciplinary field that deals with how computers can be made for gaining high-level understanding from digital images or videos. From the perspective of engineering, it seeks to automate tasks that thehuman visual system can do.

计算机视觉是一个跨学科领域，涉及如何使用计算机获取数字图像与视频中的高层次理解。从工程角度来看，它的目标是寻找一种能够与人类视觉系统实现相同功能的自动化任务。

这段话表明了计算机视觉的跨学科特点，它与人工智能、固态物理学、神经生物学、信号处理等产生诸多关联。传统的计算机视觉的处理方法多是采用信号处理方法，而机器学习技术浪潮的兴起，为计算机视觉打开了一扇新的大门。

当然，计算机视觉的数据输入源最简单和常见的就是摄像头了。但是，计算机视觉技术对于非摄像头的数据输入源也能提供很好的支持。

例如，麻省理工学院的一项研究成果能够实现基于WiFi信号探测到墙的另一侧人的动作和姿态，基于红外线传感器也能够实现人脸识别，甚至基于地震信号进行矿藏探测的技术中也可以结合计算机视觉的一些技术。

从这个角度说，计算机视觉的技术辐射度和应用范围是非常广泛的，计算机视觉技术能够使我们的生活更加多姿多彩，为创造更美好的世界提供了一个强大的工具。

02 颜色模型

我们看到的图像数据是以二维的形式展现的，这些图片有的是缤纷多彩、富有表现力的彩色图片，也有的是表现得沉郁顿挫的黑白风格，甚至有的图片只有纯黑和纯白两种颜色。诸如此类，都是图片的不同表现形式，我们将在本节具体了解一下它们的区别。

1. 彩色图像

下面，我们将介绍两种最为常用的颜色模型，分别是RGB颜色模型和HSV颜色模型。RGB颜色模型是在几何形态上呈现立方体结构，与硬件实现关联紧密。HSV颜色模型在几何形态上呈现椎体结构，更偏向于视觉上直观的感觉。

1.1 RGB颜色模型

RGB颜色模型应该是我们在平时生活中接触最多的一种颜色模型，也就是我们通常说的红、绿、蓝三原色模型。

RGB颜色模型是将红、绿、蓝3种不同颜色，根据亮度配比的不同进行混合，从而表现出不同的颜色。由于在实现上使用了3种颜色的定量配比，因此该模型也被称为加色混色模型。通过3种最基本颜色的混合叠加来表现出任意的一种颜色的方法，特别适用于显示器等主动发光的显示设备。

值得一提的是，RGB颜色的展现依赖于设备的颜色空间，不同设备对RGB颜色值的检测不尽相同，表现出来的结果也存在差异。这也就使得我们感觉有些手机屏幕颜色特别逼真、绚丽，而另一些就难以令人满意。

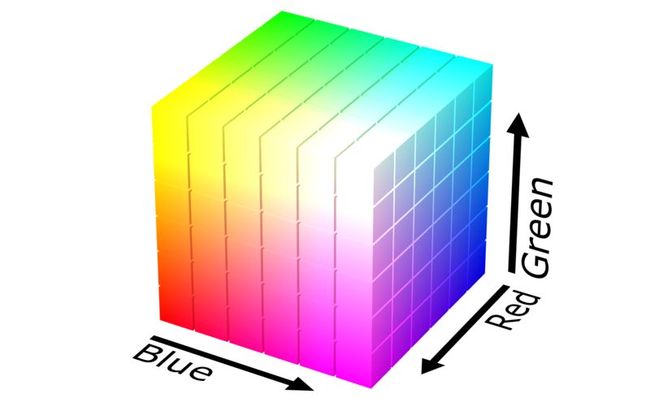
如图3-1所示展现了RGB颜色模型的空间结构，这是一个立方体结构，在该几何空间中，3个坐标轴分别代表了3种颜色。那么，从理论上讲，任何一种颜色都包含在该立方体结构中。

▲图3-1 RGB颜色模型的空间结构

接触过Web前端开发的读者可能会对RGB颜色模型有一些了解，例如#FFFFFF代表纯白色，#FF0000代表正红色。这是采用十六进制对24比特展示模式的一种表示方法。开始的两个十六进制数字位表示红色，中间的两位表示绿色，最后的两位表示蓝色，每一种颜色采用8比特来表示，3种颜色共计占用24比特。

我们平时用得最多的RGB颜色展示模式也就是24比特展示的。这种方法分别将红、绿、蓝3种颜色使用8比特无符号整数来表示。8比特无符号整数表示的范围就是0~(2^8-1)，也就是[0,255]的整数区间。

例如，使用一个元组来表示正红色，元组中元素的顺序为红、绿、蓝，则正红色可以表示为(255,0,0)。那么对于黄色这种颜色来讲，它是由红色和绿色两种颜色叠加产生的，所以正黄色可以表示为(255,255,0)。如果我们想要减少该种黄色的亮度该如何操作呢？只需要把红、绿两种颜色同时按比例减少就可以实现了。

而如果改变它们的比例配比，则可以实现混合后的颜色向某种颜色进行偏移，例如橘黄色就会更加偏向红色一些。

1.2 HSV颜色模型

HSV颜色模型大家可能不是特别熟悉，这是一种采用色调（H）、饱和度（S）、明度（V）3个参数来表示颜色的一种方式。它是根据颜色的直观特征由A.R.Smith于1978年创制的一种颜色模型。

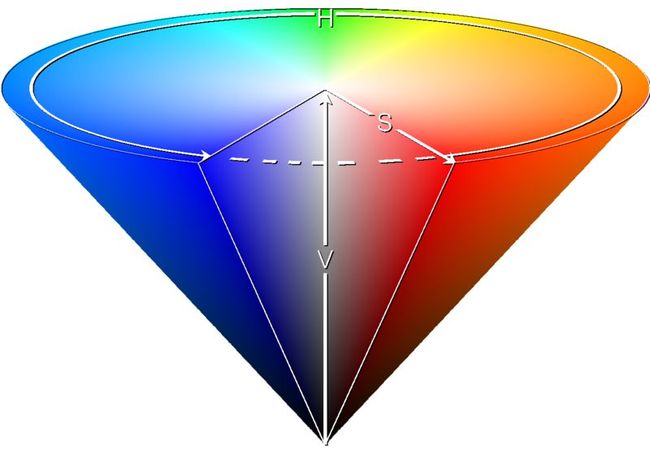
▲图3-2 HSV颜色模型的空间结构

图3-2展示了该种颜色模型的空间结构，该结构在几何形态上呈现椎体结构。

下面分别介绍HSV模型的各个参数。

（1）色调（Hue）

以角度的形式进行度量，其取值角度范围是[0,360]。红色、绿色、蓝色3种颜色以逆时针方向进行排列。例如红色的位置为0°，绿色为120°，蓝色的位置为240°。

（2）饱和度（Saturation）

饱和度反映了某种颜色接近光谱色的程度。某一种颜色是由光谱颜色与白色光的混合结果，如果某种颜色中白色的成分越少，则该种颜色越接近光谱色，表现出来的效果就是该种颜色暗且鲜艳，此时饱和度更高。反之，对于低饱和度的颜色来讲，该颜色中包含的白色成分越多，颜色越趋向白色，艳丽程度则下降。

也就是说，饱和度反映了某种颜色中白色的成分，可以用百分比0~100％来表示，该数值越高，饱和度越高，光谱颜色的成分越多。

（3）明度（Value）

明度表现了某种颜色的明亮程度，可以认为是一种由光线强弱产生的视觉体验。我们看到的颜色越明亮则明度值越高，反之则越低。例如，深紫色和桃红色两种颜色进行对比，深紫色的颜色更加晦暗，而桃红色更加明亮，则认为桃红色的明度要比深紫色的高。同样，我们也可以使用百分比的形式来表示某种颜色的明度。

这两种模型之间是可以通过数学公式进行相互转换的。通过学习这两种颜色模型，我们可以学习到计算机视觉中的基本概念，以及颜色表现的基本原理，为我们后面的学习做好铺垫。

2. 灰度图像与二值图像

在上面我们已经接触到图像的颜色模型了，以RGB颜色模型为例，可以认为一张图片的颜色是由包含了红、绿、蓝3种不同通道的颜色进行叠加混合而产生的。

从数学角度来看，对于一张彩色图片，可以认为其是由3个二维矩阵进行叠加混合而产生的，每一个二维矩阵记录了某种颜色在不同位置处的亮度值，那么3个二维矩阵就对应了该图片的3个最基本的颜色通道。

换句话说，有人说一张图片就是一个矩阵，其实这样的表述是不严谨的。对于彩色图片来讲，一张图片不仅包含了一个矩阵，而是包含了红、绿、蓝3种不同颜色信息的3个矩阵。那么，是否存在一张图片就是一个矩阵的情况呢？当然有！我们下面介绍的灰度图像与二值图像就是如此。

2.1 灰度图像

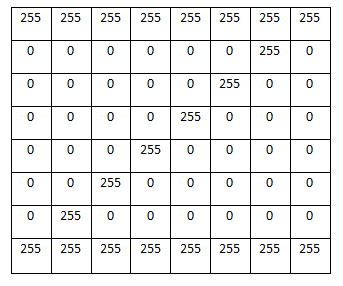
如图3-3所示，只需要用一个二维矩阵就可以表示一个灰度图像了，我们可以看到这个8×8图片所表现的图形是一个字母Z的形状。

▲图3-3 字母Z图像的矩阵表示

我们在平时接触到灰度图像的情景非常多。例如，非彩色打印的书籍中的图片就是灰度图像，黑白照片也是灰度图像。这类图片有个特点，虽然这些图片没有包含其他五颜六色的信息，但是，我们依然能够从这些图片中获取到图像的轮廓、纹理、形状等特征。

我们的直观感觉是正确的，这也说明了灰度图像相对于彩色图像缺少了具体的颜色信息，但是，灰度图像依然能够完好地展示出图像中各个部分的轮廓、纹理、形状等关键特征，同时灰度图片的存储结构相对于彩色图片更为简单。

这样便会产生一个优点，如果我们想要提取图像中的特征与颜色无太多关联，那么我们就可以选择将彩色图片处理成灰度图片的预处理方式。由于灰度图片的结构更为简单，同时关键信息又不大会损失，这样就可以极大地减少计算量。

回过头我们再来想一想，我们可以通过手机来拍摄彩色照片，同样也可以拍摄出黑白照片。在这个过程中我们可以猜想，黑白照片和彩色照片是否存在转换关系呢？答案是肯定的。我们可以通过数学公式将RGB模型中的红、绿、蓝3个矩阵进行合并，合并成一个矩阵，这个矩阵就是代表了灰度图像的矩阵。

我们知道，即便是黑色，也分为不同的等级。假如令黑种人的肤色为1代表纯黑色，白种人的肤色为0代表纯白色，那么我们黄种人中有的长得白一点的女生，她的肤色值就可以是0.2，有的长得黑一点的男生，他的肤色值就可以是0.6。

从上述的例子中，我们得出了一个结论：即便是黑色的程度也是可以量化的，介于黑色和白色之间的颜色就是灰色，那么直接量化的就是灰色的程度，这个程度就是灰度。一般的量化方法是将纯白色作为255，纯黑色作为0，在这个区间中，使用对数的方法划分具体数值进行量化。当然这个数值可以是浮点数。

从彩色图片到灰度图片之间的转化公式就可以表示为：

Igray=［0.299,0.587,0.114］·［Ir,Ig,Ib］ (3.1)

其中，Igray代表灰度图像中的灰度值，［Ir,Ig,Ib］代表彩色图像中R、G、B通道中的像素值。

式（3.1）表示了两个向量进行点乘的过程，例如图片中某一点的RGB值为（255,0,100），那么将该图片转化到灰度图片时，对应位置的灰度值为：

Igray=0.299×255+0.587×0+0.114×100=87.645

这里给出的转换系数只是一个参考值，使用不同的灰度图转换方法得到的值也是不相同的，一般常用的RGB数值比例大致为3∶6∶1。

2.2 二值图像

二值图像顾名思义只有纯黑色和纯白色两种颜色，没有中间过渡的灰色。其数据结构也是一个二维矩阵，只不过这里面的数值只有0和1两种。

二值图像是在灰度图像的基础上进一步计算的结果，计算过程比较简单，需要指定一个阈值，然后判断图片中不同点处的灰度值，如果该点处的灰度值高于阈值则该点值为1，否则为0，这样也就实现了灰度图片二值化的过程了。图3-4为一张二值图像。

可以看到，二值图像的空间占用量进一步减少了，每一个像素点只需要1比特就可以表示了，这对于表示字符这类非黑即白形式的图片具有优势。由于二值图像是在灰度图片的基础上通过阈值判断产生的，这样就会缺少细节部分，只能显示出图片的大致轮廓。不过，这个特性虽然带给我们直观的感觉是很不好的，但是，这在图像的分割等场景中具有很好的利用价值。

▲图3-4 二值图像的示例

03 信号与噪声

信号与噪声是一对敌人，图像的空间是有限的，信号多一点，噪声就少一点，反之亦然。我们在打电话中如果觉得杂音特别多，那么也就是此时通话数据中的噪声特别多，已经达到了影响正常通话的程度。甚至噪声特别大的时候，信号容易淹没在噪声中。图像也是一种数据，图像中也存在信号和噪声。本节中将具体介绍信号与噪声的相关知识。

1. 信号

信号是一个好东西，因为这是我们想要的数据。信号越多，噪声的干扰便会越少，数据的质量也就越高。我们可以使用信噪比这个概念来衡量数据质量的高低。所谓信噪比就是指信号与噪声二者能量之比值。直观来讲，噪声越少，信噪比越大，数据的质量越佳。

我们可以看到图3-5a展示的是经过高斯噪声干扰的图像，而图3-5b是未经噪声干扰的原图。

▲图3-5 受到噪声干扰的图像与未经噪声干扰的图像

2. 噪声

我们在图3-5中已经看到经过噪声干扰和未经过噪声干扰的两幅图片的差异。经过噪声干扰的图像令我们难以获取图片所要表达的原始信息，使得图像所表达信息的确定程度减少，也就是所谓的信息熵增大。

而在实际生活中，通过图像采集设备获取到的图片也或多或少会引入噪声，这主要是由摄像机等图像采集设备的感光元件受到干扰产生的噪声表现在图像上而形成的，主要表现为黑白杂点等。

图像中随机出现的黑白杂点称为椒盐噪声，“椒”代表黑色，“盐”代表白色，故而用椒盐噪声这个概念来表示图像中存在的黑白杂点，其在图片中出现的位置是随机的。而图像中也可能会随机出现某些颜色的改变。造成此类杂点最典型的就是高斯噪声，这是由于在原图片的基础上叠加了高斯噪声而造成的。

所谓高斯噪声是指图像叠加的噪声概率密度服从高斯分布，也就是正态分布。这是自然界中最为常见的一种噪声类别，例如夜晚通过照相机拍照获得的照片就可能存在该类噪声。

04 图像滤波

前面提到了噪声，噪声是我们不想要的一类数据。但是在实际操作中往往会引入噪声，例如图片经过低质量的信道传输，引入了信道中存在的噪声；图像采集设备由于某些电子学原因而引入了噪声等。

噪声的存在必然会对我们正常的图像处理造成干扰，尽可能多地滤除噪声是我们进行图像预处理的一个重要步骤。本节将给大家介绍常见的滤除噪声的方法。

1. 均值滤波

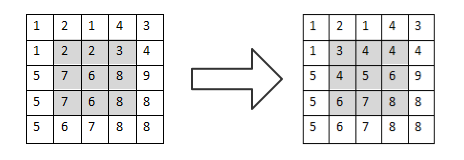
这里提到的均值滤波器更确切地说是算数均值滤波器，这是最简单的一种图像滤波方法，可以滤除均匀噪声和高斯噪声，但是会对图像造成一定程度的模糊。它是将图片中指定区域内的像素点进行平均滤波的方法，如图3-6所示。

这个过程与前面我们所说的卷积的计算过程是类似的。以图3-6过程为例，这个卷积核可以表示为：

 

▲图3-6 均值滤波过程演示

图3-6中，对左图中左上角的9个点进行均值滤波，得到右图中左上角9个点的中心值3的计算过程为：

1/9(1+2+1+1+2+2+5+7+6)=3

依次滑动这个滤波器，即可得到图3-6中右图所示阴影区域中的结果。

均值滤波器的缺点是会使图像变得模糊，这是因为它将所有的点都进行了均值处理。而实际上，在绝大多数情况下，噪声的占比是少数，将所有的点都以同样的权值进行处理，势必会导致图像的模糊。而且，这个滤波器的宽度越大，滤波后的图片就会越模糊，也就是丢失图像的细节部分，使图像变得更加“中庸”。

当然，根据这个特点，也可以将这个滤波器的权值更改一下，以便达到有所侧重的效果。

例如，在对图片进行滤波操作时，不应该全部按照系数为1进行加权求和，从而进行滤波。我们知道，图像的像素是连续的，距离越近的像素点间的联系越大，那么，滤波器的参数越靠近中心位置的权值越大，越靠近边缘位置的权值越小，根据这个思路来修改滤波器的权值的方法是否可行呢？

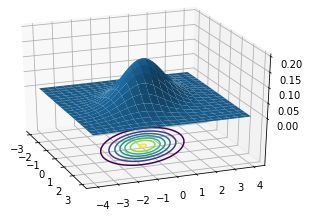
一种可行的实现方法便是将这个滤波器的参数按照高斯分布形式进行修改，那么这个滤波器就称为高斯滤波器。如图3-7所示是二维高斯分布曲面图及其投影，我们选择的滤波器权值就是高斯曲面的投影。读者可以理解为何选择高斯分布作为滤波器的权值参数。

▲图3-7 二维高斯分布示例

2. 中值滤波

我们在上面介绍了均值滤波，使用均值滤波会造成图片的模糊，即使修改均值滤波的权值，也还是会造成图片的模糊。因此，我们既要对图片进行滤波处理，又要尽量减少图片的模糊程度，那么就要考虑另外一种思路来实现滤波过程。

中值滤波是一种与均值滤波过程不同的滤波方法。相比于均值滤波，中值滤波可以有效减少图片的模糊程度。中值滤波的原理如下：

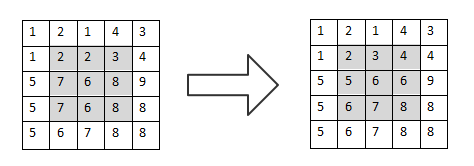
与均值滤波的原理大体相似，同样使用一个指定大小的滑动窗口，在图片上进行滑动，不断地进行滤波处理。不过，与均值滤波的不同在于，中值滤波在对像素点进行处理时，并不是采取简单的取平均数的做法，而是改为取其中位数的做法。

以椒盐噪声为例，其像素的灰度值要么是最低的，要么是最高的，总是处于两个极端。而图像中绝大多数正常点处于这样一个区间之中，因此，将滤波器所选取区域中的像素点，以其灰度值的大小进行排序，如果存在噪声，则基本处于两端的位置。

此时，这组数据的中位数在绝大多数情况下都是图像中正常的信息而不是噪声，这样就可以实现滤波过程。这个过程如图3-8所示。

▲图3-8 中值滤波过程演示

对于椒盐噪声来讲，中值滤波的效果要好于均值滤波。而对于高斯噪声来讲，均值滤波的效果优于中值滤波，这是因为，高斯噪声的特点是噪声颜色值不固定，基本符合高斯随机分布的特点，这样就会导致中值滤波无法按照默认的噪声范围进行滤波，其效果自然就没有均值滤波好。