K近邻算法的基本原理和代码
目录
1.基本原理
2. 算法原理
2.1 算法优缺点
3.总结
4.K近邻实现和探究
思想:
4.1收集数据集
4.2统一数据集大小
4.3导入数据集
4.4分割数据集
4.5K邻近算法
4.6 测试
五.实验结果及总结
1.基本原理
k最近邻(k-Nearest Ne ighbor)算法是比较简单的机器学习算法。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单:如果一个样本在特征空间中的多个最近邻(最相似〉的样本中的大多数都属于某一个类别,则该样本也属于这个类别。第一个字母k可以小写,表示外部定义的近邻数量。
简而言之,就是让机器自己按照每一个点的距离,距离近的为一类。
2. 算法原理
knn算法的核心思想是未标记样本的类别,由距离其最近的k个邻居投票来决定。
具体的,假设我们有一个已标记好的数据集。此时有一个未标记的数据样本,我们的任务是预测出这个数据样本所属的类别。knn的原理是,计算待标记样本和数据集中每个样本的距离,取距离最近的k个样本。待标记的样本所属类别就由这k个距离最近的样本投票产生。
假设X_test为待标记的样本,X_train为已标记的数据集,算法原理的伪代码如下:
遍历X_train中的所有样本,计算每个样本与X_test的距离,并把距离保存在Distance数组中。
对Distance数组进行排序,取距离最近的k个点,记为X_knn。
在X_knn中统计每个类别的个数,即class0在X_knn中有几个样本,class1在X_knn中有几个样本等。
待标记样本的类别,就是在X_knn中样本个数最多的那个类别。
2.1 算法优缺点
优点:准确性高,对异常值和噪声有较高的容忍度。
缺点:计算量较大,对内存的需求也较大。
3.总结
其算法参数是k,参数选择需要根据数据来决定。
k值越大,模型的偏差越大,对噪声数据越不敏感,当k值很大时,可能造成欠拟合;
k值越小,模型的方差就会越大,当k值太小,就会造成过拟合。
4.K近邻实现和探究
思想:
将数据集导入后,把图片展平成一维向量,然后再根据不同图片的向量计算距离,测试时循环变化K值,嵌套循环测试集,定义一个count计数预测正确的个数,最后算出预测角度。
4.1收集数据集
羽毛球数据集图片:
篮球数据集图片:
4.2统一数据集大小
import os
import re
import sys
# 统一图片格式
fileList = os.listdir(r"D:\desttop\羽毛球")
# 输出此文件夹中包含的文件名称
print("修改前:" + str(fileList)[1])
# 得到进程当前工作目录
currentpath = os.getcwd()
# 将当前工作目录修改为待修改文件夹的位置
os.chdir(r"D:\desttop\羽毛球")
# 名称变量
num = 1
# 遍历文件夹中所有文件
for fileName in fileList:
# 匹配文件名正则表达式
pat = ".+\.(jpg|jpeg|JPG)"
# 进行匹配
pattern = re.findall(pat, fileName)
# 文件重新命名
os.rename(fileName, "badmianton_" + str(num) + ".jpg")
# fileName.resize(256, 256)
# 改变编号,继续下一项
num = num + 1
print("***************************************")
# 改回程序运行前的工作目录
os.chdir(currentpath)4.3导入数据集
import numpy as np
import cv2
from sklearn.model_selection import train_test_split
import operator
import os
#导入数据集
def loding_data():
X=[]
Y=[]
for filename in os.listdir(r"D:/desttop/bascketball"): #数据集文件夹的绝对地址
filenames = 'D:/desttop/bascketball/'+filename
img = cv2.imread(filenames,1)
#进行归一化处理
img = (img - np.min(img)) / (np.max(img) - np.min(img))
X.append(img.flatten())
Y.append('basketball')
for filename in os.listdir(r"D:/desttop/badmainton"):
filenames = 'D:/desttop/badmainton/'+filename
img = cv2.imread(filenames,1)
#归一化
img = (img - np.min(img)) / (np.max(img) - np.min(img))
X.append(img.flatten())
Y.append('badmainton')
data = np.array(X)
labels = np.array(Y)
# print(labels)
return X, Y4.4分割数据集
X,Y=loding_data()
# 分离训练数据集和评估数据集
# 设置评估集占比
test_size=1/3
# 设置随机种子,保证训练集和评估集的不变性
seed=4
# 训练特征,评估特征,训练标签,评估标签
X_train,X_test,Y_train,Y_test=train_test_split(X,Y,test_size=test_size,random_state=seed)
#因为下面用到列,转换成数组
X_train = np.array(X_train)
X_test = np.array(X_test)
Y_train = np.array(Y_train)
Y_test = np.array(Y_test)4.5K邻近算法
#K邻近算法
def classify0(inX,dataSet,labels,k):
dataSetsize = dataSet.shape[0]
diffMat = np.tile(inX,(dataSetsize,1))-dataSet
sqiDiffMat = diffMat**2
sqiDistances = sqiDiffMat.sum(axis=1)
distances = sqiDistances**0.5
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted(classCount.items(),
key = operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
4.6 测试
for k in range(len(X_train)):
count = 0
for i in range(len(X_test)):
a=classify0(X_test[i],X_train,Y_train,k+1)
if a == Y_test[i]:
count += 1
ac = count / len(Y_test)
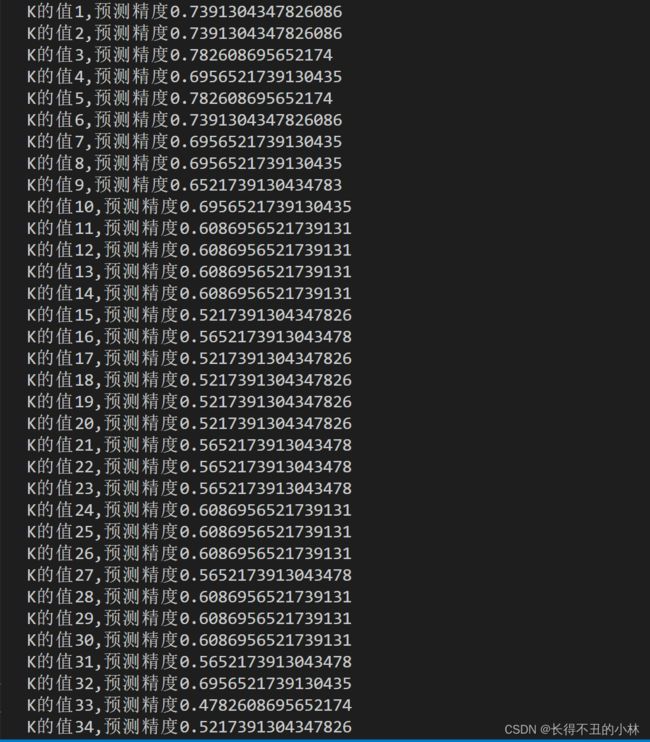
print(f'K的值{k+1},预测精度{ac}')五.实验结果及总结
1.K小的时候,预测精度很高,说明两个类别差距大。
2.K大的时候,预测精度慢慢减小,是因为数据集选择不好,图片背景影响了判断。